坐着[模型思想]的船到达[方程]的彼岸

沈青

方程是刻画现实世界中具有等量关系的数学模型。东北师范大学史宁中教授曾指出方程思想的本质与意义：方程思想有着丰富的含义，其核心体现在模型思想与化归思想方面。在教学过程中，教师要引导学生从数学的角度看问题，用数学语言去捕述自然语言，分析已知量和未知量之间的等量关系，构建等量模型去解决复杂的数学问题，既培养了学生的数学思维，义达到轻松学习的目的。何以坐着“模型思想”的船到达“方程”的彼岸呢？

一、用数学语言描述问题

从数学的角度分析问题，用数学语言去描述自然语言，将生活问题抽象成数学问题，这是我们学习数学的基本能力。数学语言是学习数学的工具，它主要分为文字语言、符号语言和图表语言。准确而简明地用数学语言去描述数学问题，往往能够使复雜问题变得更直观明了，便于我们思考。

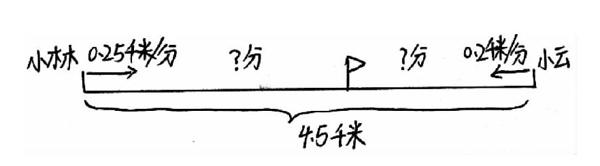
如，人教版数学五年级上册“实际问题与方程”中的例5：

小林家和小云家相距4.5km。周日早上9：00两人分别从家骑自行车相向而行，两人何时相遇？

师：读完此题，你能用自己的话表达一下题目意思吗？

生1：小林家和小云家相距4.5千米，小林每分钟骑250米，小云每分钟骑200米，早上9：00他们两人分别从家骑自行车相向而行，问他们何时相遇？

师：你说得真详细，你是怎么理解相向而行的？（师边说边指题目中的情境图）

生2：相互面对面出发。

师：你能用两只手比划一下面对面出发的运动情况吗？

（生用两只手比画着，结果两只手碰到一起了）

师：在你们用手比画的过程中，你有什么想说的吗？

生3：两只手分别代表小云和小林，他们面对面一起出发，最后相遇了。

师：你的联想能力真好！同学们同意吗？

生：（齐说）同意。

师：既然小云和小林是一起出发，相遇时停下，你觉得他们行驶的时间一样吗？ 生：（齐说）一样。

师：我想找两位同学来帮我们验证一下。（两位同学分别扮演小林和小云，在台上的两端面对面同时出发，最后相遇停下）

师小结：原来两人相向而行，同时出发，最后相遇停下，他们行驶所用的时间是一样的。

师：通过演示，你能不能用一种你喜欢并且便于理解的方式来描述一下这个运动情况呢？

（师展示并对比学生的作品，让同学相互说作品的优缺点，引导学生将已知信息和问题都标在线段图上）

通过用手比画和学生演示来解释“相向而行”和“相遇”等关键词，学生对数学语言中的“相向而行”和“相遇”有了很好的理解和体验。再引导学生用画线段图的方式来描述数学问题，把已知信息和问题都标在线段图上，使问题变得简单明了。理解题目的意思并能够用简明的数学语言表述问题，可以锻炼学生用数学思维思考问题的能力。

二、分析已知量和未知量之间的数量关系

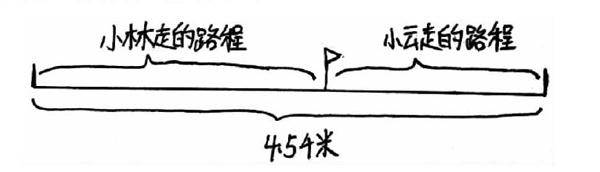
建构主义学习理论认为学习的过程是学习者主动建构知识的过程，学习者以原有的经验为基础，通过与外界的相互作用来建构新的理解。在引导学生分析已知量和未知量的数量关系时，要从条件和问题的整体出发，把已知量和未知量找出来，再来分析它们之间的相等关系。学生找出了已知量是小林的速度、小云的速度和他们两家的距离，未知量是小云和小林的行驶时间。让学生结合线段图说一说这些数量之间有什么关系，学生会想到“速度×时间=路程”。他们很容易得出小林的速度×小林行驶的时间=小林的路程，小云的速度×小云行驶的时间=小云的路程。你能在线段图上标出哪段是小林走的路程，哪段是小云走的路程吗？小林和小云行驶的总路程与他们两家相距的距离义有怎样的关系呢？

学生从自己标的线段图中很容易看出小林走的路程+小云走的路程=4.5km。“温故而知新”，从原有的知识经验出发，不断引发新问题，在新问题与旧知识之间产生联系，解决新问题就是自主获得新知识的过程。

三、构建等量模型——列方程

通过分析数学问题中的已知量和未知量之间的等量关系，从而构建等式去求解未知量，这是列方程解决问题的实质。我们用画线段图的方式分析出小林走的路程+小云走的路程=总路程（两家相距的距离），根据这个等量关系来列方程解决问题。我们不妨设小林和小云的行驶时间为x分钟，则：

小林的速度×小林行驶的时间+小云的速度×小云行驶的时间=4.5km

O.25x+0.2x=4.5

列方程的关键是建立数量之间的等量模型，用数学符号建立方程，使已知数和未知数都参与到等式的计算中再根据等式的性质，利用化归思想求解出未知数。

四、反思与总结

美国教育心理学家布鲁纳指出：掌握基本的数学思想和方法，能使数学更易于理解和更利于记忆，领会基本数学思想和方法是通向迁移大道的“光明之路”。类似相遇问题的还有：打字问题、挖隧道问题和做零件问题等。虽然它们情境不一样，但都是运用“一部分+另一部分=总的”这一模型思想来解决问题，这就是领会模型思想后迁移的结果。在小学数学教学中，我认为最重要的是数学思想方法的领悟，以及如何用数学思维去思考数学问题，这比知识本身更加重要。让学生学会用数学语言去捕述数学问题，分析已知量和未知量之间的等量关系，用数学符号建立方程，才能算是真正意义上的列方程解决问题的学习。

在我们的小学数学教学过程中，过于强调知识本身，或多或少地忽略了其背后所体现的数学思想方法，这是导致学生从低年级学段很难顺利过渡到高年级学段的重要原因。教师在教学中过多地强调知识，会让学生对知识的理解停留在表面，对数学的学习无法达到一个新的高度。学生只有真正明白数学学习的本质及其意义，体会数学思想方法，才能更好地去吮吸知识、利用知识来解决生活问题和数学问题，发现数学的美。