数形结合思想在初中数学教学中的应用

赵学静

摘要：初中阶段，数学学习相较于小学学习已经具备一定的难度，主要表现在对学生抽象性和逻辑性思维的要求。为了保证初中数学教学的效果，教师也采取多样化的教学方法，数形结合便是一种有效的数学教学方法，也是数学的一种解题思路。将数学内容与图形的方式展现出来，让学生直观地看到数与形之间的关系，有助于学生理解复杂的数学知识，提升学生的数学兴趣。本文主要研究数形结合思想，探究数形结合的意义以及初中数学如何有效应用数形结合思想。

关键词：数形结合 初中数学 教学应用

数学学科不同于其他学生，对于学生的素质要求比较高。初中数学做为一种与现实生活联系密切的学科，里面的许多数学知识都可以用于指导生活实践。因此，做好初中数学教学，提升学生数学素养很有必要。现阶段，数学学科在部分学生眼中，是一门难懂枯燥的学科，原因在于数学有着许多的公式和概念，尤其是是一些抽象性的内容，学生理解起来存在难度。教师需要采取有效的措施，解决这一问题。数形结合思想便是一种提升教学效果，帮助学生理解数学知识的一种途径。数形结合思想就是教师通过板书绘画或者多媒体设备等方式，将数学知识图形化，将数学语言、数学变量等以图形的方式展示，方便学生理解。数形结合思想在数学教学中的应用十分广泛，许多知识都可以采用这种教学方法，对于优化数学教学，提升教学效果有着很好地促进作用。例如，实数教学，可以利用数轴进行教学；函数教学，可以利用图像展示变量与图形的关系等，方便学生理解和掌握相关数学知识。

一、初中数学教学应用数学结合思想的作用

数形结合思想对于学生学习数学有着很大的帮助。数形结合可以将抽象的概念具体化和完整化，可以用于解决某些问题，成为重要的解题思路，也可以培养学生学习数学的兴趣，对于学生数学素养的培养起到积极作用。

（一）数学结合思想有助于学生学习和理解数学概念

数学概念是学生学习数学的基础，也是数学知识点的一种总结。通常情况下，数学概念以文字的方式表达出来，这种表达方式，有着一定的严谨性，但是对于学生而言，理解起来就需要费很大的功夫。容易让学生觉得数学知识太抽象、太枯燥，比较难懂。因此，可以利用数形结合的方式，也就是将“数”和“形”对应起来，文字描述配合直观模型的方式，帮助学生去理解文字概念，掌握概念的本质。以数轴的教学为例，人们利用秤杆上的点用于衡量物品的重量；利用温度计的点衡量温度的高低。秤杆和温度计看似互补关联的东西，但都有着数量关系，都包括“度量的起点、单位、方向”，这两个就可以作为数轴的模型，有原点、有单位长度、有方向，辅助“数轴”的知识教学。

（二）为学生提供新的解题思路

数学知识学习本身就是更好地应用数学知识解决现实问题，学生对于知识的理解情况，直接影响着学生的解题能力。数形结合的思想對于学生而言，是一种很好地解题思路，可以帮助学生快速地找到解题的关键。数学结合的思想在于“数”与“形”的转化，通过图形，更好地反应变量之间的关系。在一些函数关系中，数形结合的方法十分常见。例如，在一元二次不等式的教学中，可以利用一元二次方程和函数图形，解答一元二次不等式。Ax2+bx+c=0，可以将其视为y=Ax2+bx+c函数，y=0的特殊情况，而将一元二次不等式Ax2+bx+c>0和Ax2+bx+c<0，可以视为y=Ax2+bx+c函数，y>0或者y<0的特殊情况，画出二次函数y=Ax2+bx+c的图像，可以直观地看到，变量x变化是，对应的y值变化，也可以看到特定区间内的y值，对应的x的区间范围。

二、初中数学教学中数形结合思想的应用策略

（一）教学中巧妙导入数形结合思想

为了保证数形结合思想可以做到事半功倍，取得好的教学效果，需要教师在教学环节，巧妙地导入数形结合的思想。对于学生而言，学生对于数形结合思想并不了解，需要教师将这种教学思想和解题思路传授给学生，以数与形的方式，辅助教学。例如，教师在进行正负数的教学时，便可以采用数形结合的方式，教师利用数轴，在黑板上画出正负数的位置，并通过具体的例子，让学生认识到零、正数和负数在数轴的不同位置。学生在比较-1和-2，谁大谁小时，便可以利用数轴，画出两个数的位置，-1和-2都在数轴的左侧，数轴往左数值越小，根据比较-1和-2的位置，可以清晰的看到，-2位于-1的左边，因此，-2是小于-1的。

（二）数形结合思想的发展

初中数学同样也是一个数学知识难度不断提升的阶段。学生在初中阶段，接触到方程概念，在初次学习方程式时，学生往往难以理解。因此，可以采取数形结合的方式，让方程组的求解过程变得简单。以数轴的方式，画出方程的图形，通过与数轴的交点，得出方程组的解。在初中数学教学中，还会经常遇到一些追击问题、浓度问题、路程问题，单纯从文字方面讲解，理解存在难度，一边讲解，一边同图形的方式，画出对应的关系，这种数形结合的方式，更适合学生理解，理清问题的思路，更好地解答问题。

（三）数形结合思想的升华

函数教学是代数教学的内容，也是学生普遍认为难学的内容，在函数教学中，数形结合思想的应用，则可以将变量与图形的关系直观地展现出来，方便学生理解、学习、解题和验证。在函数教学时，经常会利用到函数图像，这种数形结合的方式，有助于学生更好地掌握函数的特点，掌握变量的关系。进而学生可以做到举一反三，用数形结合的思想，去解决其他的函数问题。

可以看出，数形结合在初中数学的应用，应该是从简到难的一种过程，首先培养学生的数形结合思想，让学生认识到利用数形结合可以更好地理解教学内容。其次在数学知识难度和层次提升的同时，继续使用数形结合思想。最后，学生理解这一思想，将其做为一种学习和解题的辅助。这样便实现了数形结合思想在初中数学教学的渗透。

三、数形结合思想在初中数学教学的应用案例分析

可以说，初中学生已经部分掌握了数形结合的知识，可以利用一些学习工具，比如，直尺、量角器、三角板、圆规等绘制图形，用于理解数学知识和进行数学知识的解题。上文我们已经提到，可以利用数轴，学生理解实数的关系、理解一元一次方式、解题一元一次不等式等，就是运用到了数形结合的思想。下面我们通过具体的数学案例，分析数形结合思想的具体应用。

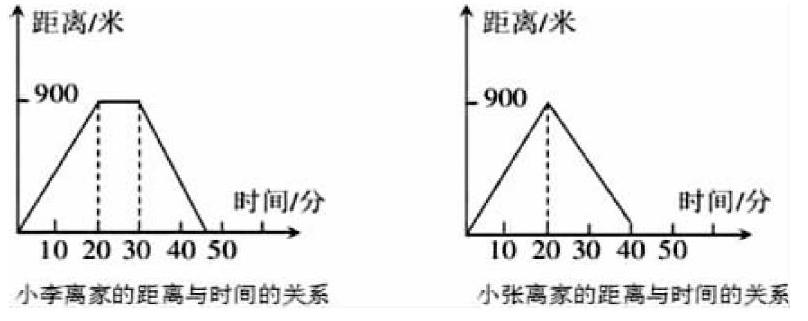
数学案例：小李和小张是两个好朋友，每逢周末两人都要相约一起游玩。某个周末，小李和小张从家里走了20分钟，来到了一座离家900米的桥边，小张觉得桥边没什么好玩的，便选择以原先的速度回家，小李自己在桥边游玩10分钟，想到自己还有没有完成的作业，便回了家，用时15分钟。请利用平面直角画出小张、小李离家的时间和距离的关系。

这个案例是生活中经常遇到的问题，教师让学生通过数形结合的思想，绘制出距离与时间的函数关系，帮助学生更好地理解题意，方便学生进行习题解答。通过这种基础性的联系，让学生逐渐掌握数形结合的思想，为后面的函数学习打下基础。

四、结语

综上所述，数形结合思想既是一种重要的教学思想，可以将之用于辅助教学活动的开展；又是一种重要的解题思路，用于解题和验证答案。初中阶段的数学已经具备一定的难度，为了保证数学教学的效果，教师可以采用数形结合的教学方法，让学生更好地理解数学概念和内容，使数学教学做到事半功倍。数形结合思路可以帮助学生学习和理解抽象的数学概念，同时也帮助学生利用数与形的关系，解决数学提升。初中数学教学应用数形结合思想，需要做好循序渐进。首先，巧妙地引入数形结合思想。利用数轴，让学生理解基础的数形结合思想。其次，随着知识层次的深入，继续发展数形结合思想。最后，学生掌握数形结合思想，用于解决数学习题。

参考文献：

[1]李雪.初中数学数形结合思想教学研究与案例分析[D].河北师范大学，2014.

[2]石丽娟.谈新课标下的初中数学“数形结合”思想[J].试题与研究：教学论坛，2013，（34）：40-40.

[3]李永生.初中数学数形结合解题思想的应用分析[J].中学生数理化（教与学），2014，（12）：132-132.

[4]吴舒静.初中数学数形结合教学策略分析[J].赤子（上中旬），2015，（22）.

[5]胡秀娟.初中數学数形结合思想教学研究与案例分析[J].读与写：上，下旬，2016，（23）.

[6]姜风华.浅谈初中数学数形结合教学模式的应用策略[J].中国校外教育旬刊，2015，（11）：109-109.

[7]邓明荣.初中数学中数形结合教学方式作用[J].都市家教月刊，2015，（11）.

（作者单位：姜各庄镇姜各庄初级中学）