基于MVO的表贴式Halbach永磁同步电机优化设计
胡致远,杨向宇,赵世伟,裴云庆,曹江华
(华南理工大学 电力学院,广州 510640)
0 引 言
Halbach阵列是一种特殊的永磁体阵列磁化方法[1],用于提高永磁电机的性能。近年来,为了适合不同的应用场合,各种Halbach阵列充磁的新型永磁电机被研发出来[2-5]。最初的Halbach磁化阵列采用连续结构,考虑到Halbach阵列磁化困难,在实际应用中通常采用离散形式[6-7]。Mellor, P.H.提出了一种主极和辅助极不均匀的Halbach阵列[8],通过实验和仿真证明,通过调整每极分块方式和块间气隙来降低永磁电机谐波失真率是可行的。
Halbach阵列电机的分析通常采用解析法进行分析。考虑到电枢齿槽效应对电机气隙磁密的影响,学者们通常采用保角映射[9]的方法来提高解析结果的准确性,并通过仿真验证了该方法的有效性[10]。
随着计算机运算能力的日渐强大,人工智能的发展速度和技术的更新换代速度越来越快,更多复杂问题可以用更加智能和科学的方法来解决。遗传算法(GA)在电机优化方面已应用多年,对于解决非凸问题有许多优点。但不同的问题有不同的特点,目前没有一种优化算法可以解决所有优化问题,即无免费午餐定理(NFL)[11],因此,研究人员改进现有的算法以提供更好的结果。本文采用了一种新的元启发式优化技术MVO用于优化电机的结构。
1 电机模型和主要参数
本文采用一种五块不等厚永磁体间隔排列,并以几何中心对称的方式来合成一极磁场。每块永磁体的充磁角度符合永磁体的每一极被分成不同角度和厚度的五块。块与块之间有一个低于1度的气隙。如图1(a)所示,该结构有6个参数需要确定。k2为块①与块②之间的厚度比例;k1为块①与块③之间的厚度比例。m为块①的左边缘点,n和a分别为块②的右边缘和左边缘点,b为块③的右边缘点。电机主要参数如表1所示。为了设计出合理的电机结构,变量之间的约束条件如下:
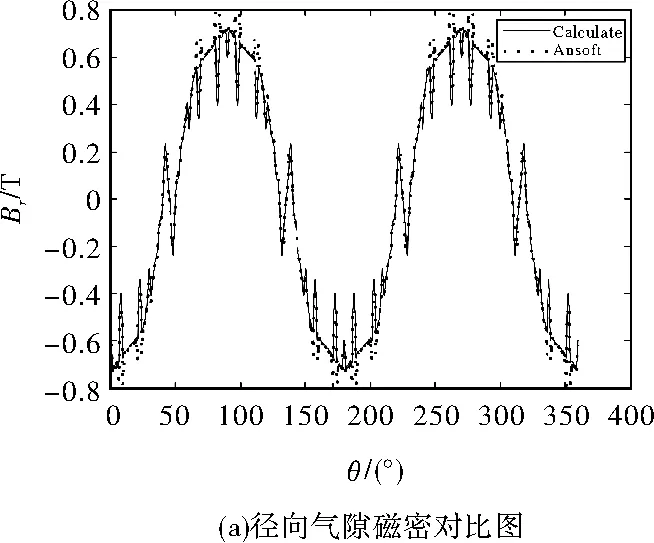
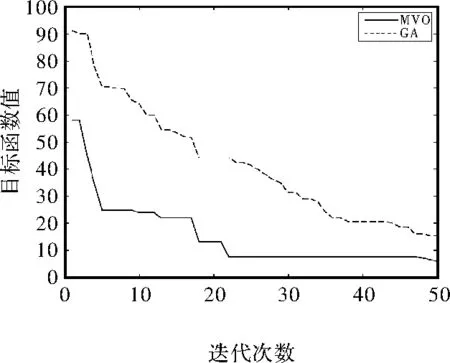
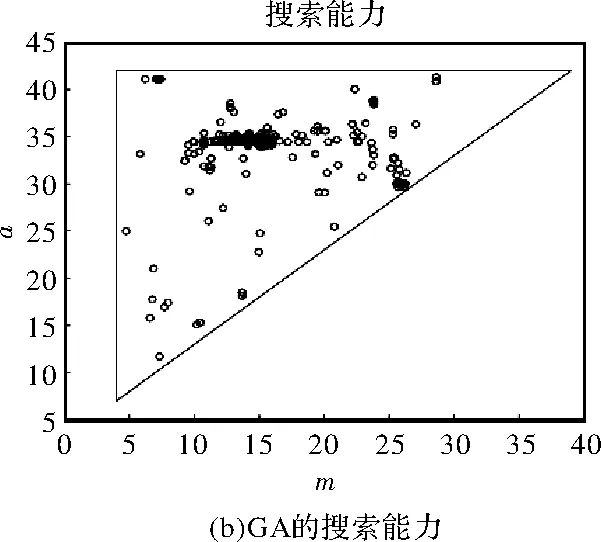
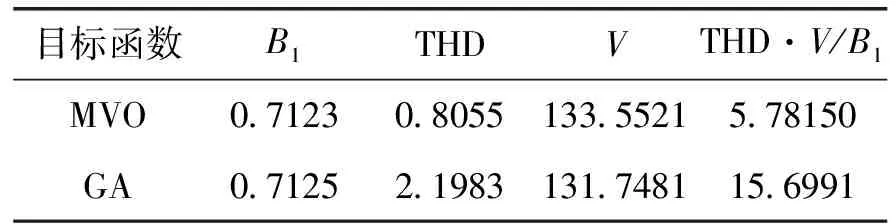
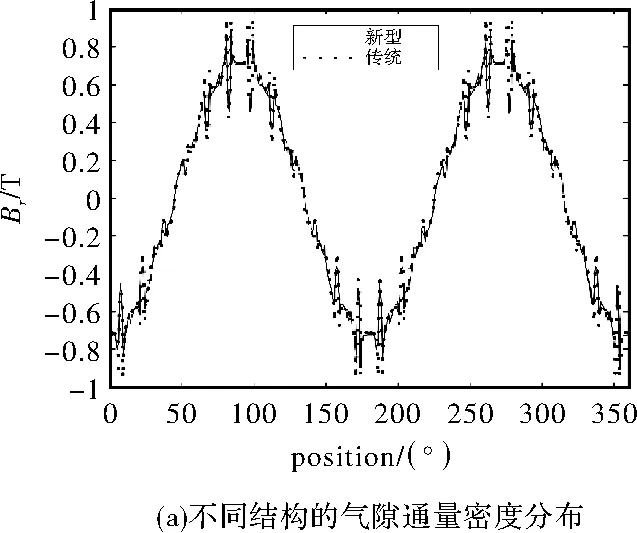
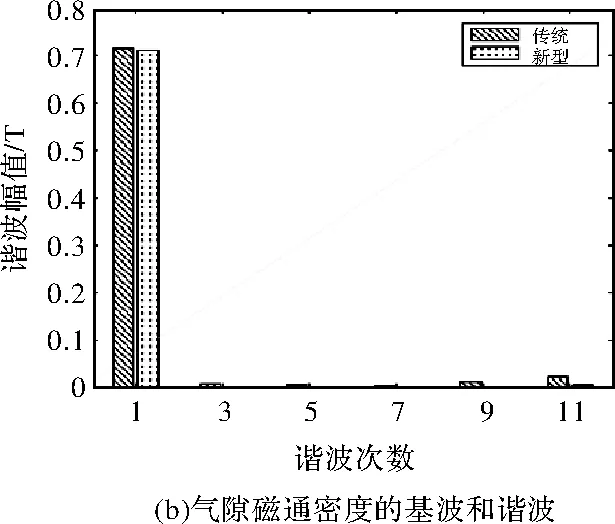
0 (1) 0 (2) m>4° (3) n-m>3° (4) b-a>3° (5) 为了满足基本要求,块①的厚度的最小值是2.5 mm。每块的瓦型结构是平行充磁的。如果θ的永磁体的几何中心,其磁化方向为θm=(1-p)θ,式中p是电机极数,在本文中取p=2,如图1(b)所示。 表1 电机主要参数 图1 电机结构 对于表贴式永磁同步电动机,为了建立其简单的数学模型,现对电机作如下假设: (1)忽略定子铁心的齿槽效应。 (2)假设电机的气隙是均匀分布的。 (3)假设铁心磁导率无穷大。 (4)忽略永磁电机漏磁的影响。 以永磁体和气隙为求解区域,气隙中: (6) 式中,μ0为空气磁导率,B1和H1分别为气隙中的磁通密度和磁场强度。 在永磁体中: (7) 式中,M0为永磁体剩磁。B2和H2分别为永磁体中的磁通密度和磁场强度。 (8) 式中,Mr为M0的径向分量,Mθ为M0的切向分量。对于离散型Halbach表贴式永磁同步电机,如图1所示。径向和切向磁化分量可表示为式(9)和式(10)。 (9) (10) 式中,Mr为偶函数,Mθ为奇函数,它们的傅里叶展开式仅包含恒定分量和奇数项(偶数项),其结果如下所示: (11) (12) 其傅里叶系数的计算结果如下所示: (13) 结合式(3)到式(15),电机内部的合成气隙磁密为各部分结果的叠加,其解析结果为式(16)到式(18)。其中Bθ和Br分别为空气域气隙磁密的切向分量和径向分量。其中Rk为各永磁体外表面至铁心中心的长度,其中k∈[1,2,3]。无齿槽效应的气隙磁密的有限元分析结果和解析结果的对比如图2所示。 (14) (15) (16) (17) (18) 图2 气隙磁密 保角变换是一种强大的分析方法,已在现代技术的多个领域内应用。保角映射能够将复杂区域转换成简单区域。Schwarz-Christoffel变换是将多边形上表面变换为多边形内部的变换[12]。将定子槽简化成开槽无限深的模型,此无限槽深的槽口宽度等于实际槽口的宽度,因为定子槽的磁场基本集中在槽口附近,所以此简化方法对结果的影响不大。以修正上述分析结果。计及齿槽效应的磁通密度Br与不计齿槽效应的磁通密度Bk之间的关系为: (19) 式中,λ*为气隙磁导复数。这里认为槽口是无限深的。 为了得到上式中的气隙磁导复数,需要四个步骤,首先是由S平面变换到Z平面。 z=ln(s) (20) 其中,s=m+jn=rejθ,z=x+jy。 通过Schwarz-Christoffel变换,将Z平面变换到W平面如下所示: 该药的局部用药方法为腹腔镜下或超声辅助下妊娠囊穿刺注射,可把胚胎直接杀死。近几年,在该药的局部给药治疗中,经超声辅助穿刺用药最常用,于超声辅助下明确穿刺路径,把穿刺针置入输卵管胚囊后,尽可能吸光囊内积液,再把10~50 mg MTX溶于2~4 ml的0.9%氯化钠溶液内,并注入胚囊里。局部给药时无需进行麻醉,能直接作用于异位妊娠包块中,使病灶获得较高的药物浓度,因此具有见效时间短、疼痛轻微、费用低等优势,且具有治疗时间相对短的特点。有文献指出,治疗未破裂型异位妊娠,经超声辅助下穿刺注射甲氨蝶呤的治疗效果优于肌肉注射,操作便捷,准确安全。 (21) (22) (23) (24) 然后,从W平面变换到T平面: (25) 最后,由T平面变换到K平面如下: k=et (26) 结合式(20)至式(26),气隙磁导复数的计算如下: (27) 计及开槽的电机空载气隙磁密波形如图3所示。 图3 计及开槽的电机空载气隙磁密 NFL理论已经证明,没有一种优化算法可以解决所有的优化问题。这一理论显然使电机优化设计问题变得非常开放,研究者可以改进原有的优化算法或发现新的自适应优化算法来解决优化问题,使电机设计更加科学高效。考虑到遗传算法的早熟收敛性、局部搜索能力差和种群同化较晚,2015年Seyedali Mirjalili首次提出了一种新的自然启发算法,称为MVO[13]。 在多目标优化中,局部搜索和全局搜索之间的权衡是很难处理的。不同的局部搜索和全局搜索的匹配将导致不同的搜索算法,如粒子群算法(PSO)、遗传算法(GA)、蚁群算法(ACO)和模拟退火算法(SA)[14-15]。Seyedali Mirjalili比较了MVO算法与上述算法的搜索能力,证明了该算法在处理不同复杂函数时的优越性。此外,该算法被用来解决一些结构优化问题。Indrajit N.Trivedi.还利用MVO算法处理电力系统的无功优化问题[16]。本文首先将MVO算法应用到电机设计过程中。 假设每个解都是一个宇宙,解中的每个变量都是该宇宙中的一个对象。该解所对应的目标函数值被指定为宇宙膨胀率。此外,迭代次数被宇宙学中的术语‘时间’来代替。 正如GA一样,白洞的产生是由轮盘轮机制决定的。在每次迭代中,根据宇宙的宇宙膨胀率对各个宇宙进行排序,由赌轮盘选择其中之一以形成白洞。 通过上述机制,黑洞和白洞将不断地交换物体而不受扰动。为了增强全局搜索能力,认为每个宇宙都有虫洞随机地穿越空间传送物体。为了提高算法的局部寻优能力,本文只考虑被选择的宇宙和最优宇宙之间建立虫洞。这一机制的运行公式如下: (28) (29) (30) 式中,l为当前迭代次数,L为最大迭代次数,p为迭代的精度。max和min分别是虫洞存在可能性的最大值和最小值,本文将其设定为min=0.7,max=1,其中min可调,范围0-1。 MVO在电机优化设计中的操作步骤如下: 第 1步:随机创建宇宙并获得第一次迭代的最佳宇宙个体。 第2步:计算所有宇宙个体的膨胀率。 第3步:更新W和T的值。 第4步:交换黑洞和白洞内的物体。 第5步:选定宇宙通过虫洞连接最佳宇宙。 第6步:如果迭代次数达到了设定值,则最优个体将被选出,否则它将返回到步骤2。 此外,在进行全局搜索和局部搜索时,搜索范围必须满足电机的结构要求,因此,在计算目标函数之前,必须检查一些约束条件。 因此,本文将优化目标函数设定:THD*V/B1,其中THD为气隙磁密谐波畸变率,V为永磁体体积,B1为气隙磁密基波幅值。 本文通过两种不同的优化算法(MVO和GA)对电机进行了优化。在本节中,将比较两种算法搜索能力和优化结果。并通过有限元分析,将优化后的结构与传统结构(均匀Halbach结构)进行了比较。 通常,迭代次数应该选择为合适的值。次数不能太多,因为它不能反映两个最优过程的差异。然而,次数也不能太少,因为它可能不会收敛。为了反映MVO的效果和优点,将迭代次数设置为50次。 图4 目标函数值的搜索轨迹 图4为目标函数值的搜索轨迹和收敛曲线。从图中可以看出,MVO算法能够在早期就找到较低的目标函数值,在第50次迭代次数时能够找到比GA更优的解。 图5 MVO和GA的搜索能力 MVO和GA的搜索能力的对比结果如图5(a)和图5(b)所示。MVO和GA的总体种群数为20,迭代次数为50,所以有1000个搜索点。该图显示了50次迭代的搜索过程,反映了全局搜索和局部搜索能力。图5(a)为变量m和a中MVO的搜索能力,图5(b)为变量m和a中GA的搜索能力,红圈表示搜索点,红线表示问题域。从图6(a)中可以看出,MVO的搜索范围甚至扩展到边界处。此外,任何两红圈之间都有一定的距离,这反映了它的全局搜索范围是均匀分布的。图5(a)中有一个相对较大的密集区域,反映了局部搜索能力。可以看出,即使是密度较大的区域,任何两个搜索点之间仍然有一定的距离,当接近密度较大区域的中心时,距离逐渐减小。这种搜索模式非常适合于求解电机优化问题。从图5(b)可以看出,GA不能搜索求解领域的全部区域,搜索点都集中在相对较小的密集区域,这可能是由于遗传算法陷入了不是最优解的局部收敛区域。 优化后的电机结构的设计变量结果如表2所示。其目标函数值如表3所示。从表2中可以看出,GA得到的结果与MVO得到的结果有一定的差异。从表3可以看出, MVO优化的电机性能优于GA。 表2 表3 图6显示了在相同永磁用量的前提下,传统均匀Halbach结构与新型不均匀Halbach结构的性能对比。图6(a)为不同结构的气隙通量密度分布。可见,新型结构都能使气隙磁通密度更接近正弦波形。通过对波形的分析,可以得到气隙磁通密度的基波幅值和谐波幅值,如图6(b)所示。从图6(b)可以看出,非均匀Halbach可以得到几乎相同的基波幅值,但气隙通量密度的3、5、7、9、11次谐波幅值几乎全部降为零,比均匀Halbach的要好。 图6 不同结构气隙磁密 本文引入了先进的MVO算法首次对电机领域进行了优化设计。分析结果表明,在一定的迭代次数下,MVO方法能取得比GA较好的优化结果。 基于二维有限元仿真结果表明了所提出的非均匀Halbach阵列结构比传统的均匀Halbach阵列永磁同步电机具有更好的性能。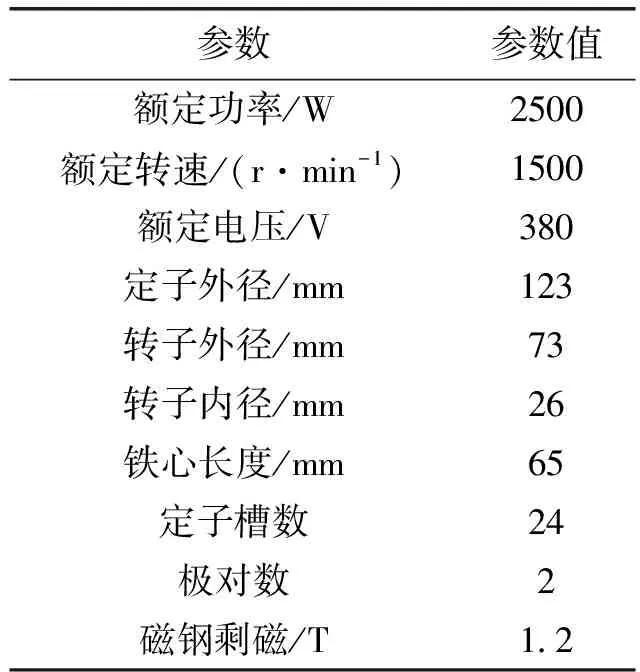
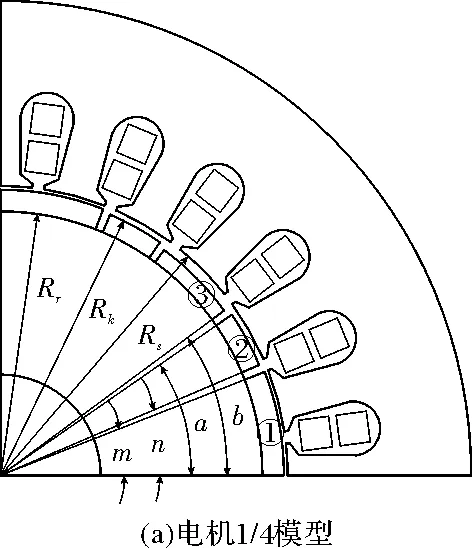
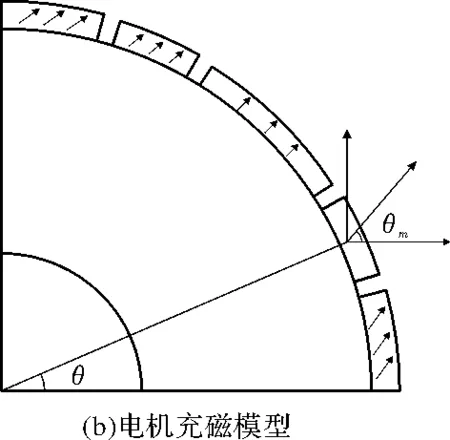
2 不计齿槽效应电机模型解析

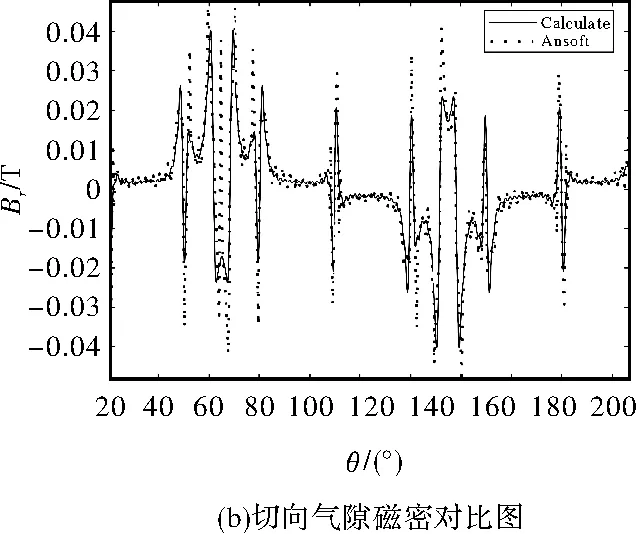
3 计及齿槽效应电机模型解析
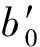
4 基于MVO的算法优化
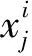
5 结果比较


6 结 论

