社会再生产视角下的经济波动：一个马克思主义RBC模型

乔晓楠 王璟雯

一、引 言

马克思主义政治经济学以社会再生产的独特视角来审视经济增长，认为经济增长的本质就是持续扩大的社会再生产过程。在将商品生产划分为两大部类的基础上，马克思进一步对每一部类中的不变资本、可变资本以及剩余价值之间的比例关系进行了探讨。当可以维系社会再生产持续运转的比例关系无法被满足时，将导致经济波动，即由“比例失衡”所引发的经济周期。社会再生产不仅反映了“经济总量”的扩张，而且还蕴含着“经济结构”的变化，因此上述洞见对于理解现实经济运行具有重要的理论意义。

长期以来，社会再生产理论一直都是中国政治经济学研究的重要领域之一，可以将其划分为三个阶段。第一个阶段为计划经济时期，当时主要关注农业、轻工业与重工业的比例关系，于是关于社会再生产的研究内容涉及简单再生产与扩大再生产、内涵式再生产与外延式再生产、固定资产动态与劳动手段协调、积累与消费及其同社会产品、经济增速之间的关系等(刘国光，1961、1962；董輔礽，1963a、1963b；黄仲熊，1963；李学曾，1963；刘 诗白和柴詠，1963；梁文森，1964)。第二个阶段为改革开放之后的经济转型时期，该阶段同样关注产业间的比例关系，但不同于制定计划的需要，而主要是判断其是否合理，同时还将许多新问题与新情况纳入社会再生产理论之中，进行诸多方面的创新性探索。内容涉及对生产资料生产部门优先增长的反思、横向经济联合以及集中与竞争的关系、企业资金循环对再生产的影响、不同劳务特点的区分、社会再生产与人口变化的关系、三大部类的拓展、引入国际贸易的拓展以及与西方经济学经济增长理论的比较等(吴树青，1980；王大安，1980；冯浩华，1980；邢俊芳，1981；方民生，1982；郭继严，1979、1983；牟以石，1983；康亦农、许昌明，1984；王慎之，1985；薛敬孝，1986；蔡钤，1986；宋则行，1987；石景云，1988；杜亚斌，1995；胡钧，1996)。第三阶段为市场经济逐渐成熟时期，特别是近期结合“供给侧结构改革”的提出，一些研究运用社会再生产理论对此进行分析。内容涉及社会再生产与有效需求、两大部类顺序与对比增速、基建部门的再生产、劳动力的再生产、提高工资收入占比等(裴小革，2013；张衔，2015；张平、郭冠清，2016；张俊山，2016；陶为群，2016)。由此可见，无论是在计划经济时期，还是经济转型时期，抑或是面临市场经济，社会再生产理论都成为研究经济运行的一种重要理论工具。

本文试图基于马克思主义政治经济学的基本理论，构造一个以分权经济为基础的分析框架，进而在引入技术冲击的条件下，观察社会再生产的比例结构变动以及经济波动。所谓RBC指实际商业周期(Real Business Cycles)，其含义为经济波动由经济中的实际成分变化所导致，而与货币成分无关。毫无疑问，RBC是过去三十年多年来宏观经济学研究的重点，其基础分析框架由Kydland和Prescott(1982)以及Long和Plosser(1983)等奠定。并且，由于其可以有效地克服“卢卡斯批判”，赋予宏观经济分析以微观基础，同时还考虑了跨期最优规划以及随机冲击的影响，因此建立在RBC基础上的DSGE(Dynamic Stochastic General Equilibrium)分析范式已经成为宏观经济学的主要分析工具①虽然近期DSGE遭到一些批评，但尚未找到更为有效的替代性工具。。

然而，需要注意的是建立在西方经济学基础上的RBC模型与本文所研究的马克思主义RBC模型存在着显著差异。概括而言，这主要体现在以下三个方面:第一，马克思主义RBC模型纳入了两大部类，并且以社会再生产为基础考察经济波动，因此这是一种多部门的结构模型。第二，马克思主义RBC模型不仅关注产出层面呈现出的波动特征，而且还涉及以“劳动价值论”为基础的价值层面的波动，即以无差别的人类劳动衡量的经济波动。第三，马克思主义RBC模型虽然也视技术变动为导致经济波动的原因之一，但是更加重视生产关系对经济波动的影响，因此本文将考察在不同劳资关系情境之下经济波动特征的差异。

二、文献综述

由于经济波动与经济增长密切相关，因此RBC模型需要建立在经济增长理论的基础之上。其内在逻辑如下:首先，经济增长理论关注的核心问题是如何进行跨期决策，当期消费增加可以改进当期的福利，但是不利于积累并实现扩大再生产，进而影响到未来的产出与消费。其次，经济增长中涉及的跨期最优化问题实际上按照“集中经济”的分析思路展开，即从社会计划者的角度，依据社会福利的最优化进行决策。这显然与市场经济条件下微观主体的个体决策存在着差异。因此，需要将“集中经济”模型转化为“分权经济”模型。最后，基于“分权经济”模型进一步引入“实际成分”的随机冲击，进而构建出RBC模型。

按照以上理论逻辑，马克思主义RBC模型需要以马克思主义经济增长理论作为基础。为此，本文将主要基于马克思主义最优经济增长理论进行建模。该理论由一批日本学者于本世纪初创立，经过持续十余年的不断发展，目前已经形成一个相对完整的理论框架(乔晓楠、何自力，2017)。山下和大西(2002)以及大西和山下(2002)最早开发了该理论的“集中经济”模型。这个模型将社会再生产的两大部类引入经济增长的分析之中，并且秉承劳动价值论，将第一部类产品设定为仅由劳动创造，而作为其产品的生产资料，即被物化的劳动，将在第二部类的生产过程中作为中间投入与劳动相结合，共同生产消费资料。由第二部类生产的消费资料被用来满足人们的最终需求，而第一部类生产的生产资料则只在生产过程中加以利用。基于以上设定，影响经济增长效率的关键是给定技术水平与劳动总量的条件下，在每一期中如何确定两大部类中的劳动配置比例以实现经济的动态最优化。换言之，上述最优劳动配置比例的求解可以理解为对生产资料的动态最优积累路径进行决策。因此，大西(2010、2015)以及金江(2013)曾以此研究两次工业革命对经济最优增长路径的影响。

金江(2008、2013)在“集中经济”模型的基础上，构造了“分权经济”模型。在分权经济模型中包含从事两大部类生产的企业以及家庭，共三类经济主体，并由其分别进行决策，进而实现各个市场的均衡。其中劳动的配置由均衡劳动回报实现，即在两大部类企业中就业将获得同样的报酬。

山下(2005)最早在马克思主义最优增长理论中引入了阶级与剥削。其建模的思路为将家庭部门分为两类，即资本家与工人，二者的差异体现在资本家更多地占有了生产资料。因此，工人在生产中受制于生产资料的缺乏而无法提高效率，只能获得较低的产出水平。于是，工人将通过借贷，向资本家租用生产资料，由于资本家处于更为强势的地位，所以由此提高的工人劳动产出将被资本家占有，进而构成工人因借贷而向资本家缴纳的租金。这样虽然有利于生产资料配置的优化，却导致资本家剥削了工人的劳动。显然，在对剥削本质的认识上，马克思主义最优经济增长理论基本秉承了马克思主义政治经济学的传统。例如，大西和藤山(2003)与松尾(2007)就都指出资本家对于工人部分劳动成果的无偿占有就是剥削。并且，大西(2010、2015)和田添(2011)也进一步证明导致剥削的根源在于资本家对生产资料的占有，如果两个阶级最终的单位活劳动对应的生产资料存量逐步收敛趋同，那么剥削也将随之消失。

以上研究虽然考虑了社会再生产以及剥削，但还缺乏价值层面的分析。于是，马克思主义最优增长理论进一步将“价值”概念导入，分别确定两大部类单位产品所包含的价值量，进而对简单和扩大两种形式的再生产比例结构进行讨论(金江，2008、2010、2011、2013；岡森，2011；田添、大西，2011)。需要说明的是上述导入“价值”概念的模式与之前的数理马克思主义政治经济学一脉相承。如果去比较马克思主义最优经济增长理论与分析马克思主义学派的建模方法，就不难发现二者在本质上具有共通之处，其差异仅体现在刻画实物生产技术方面是否采用生产资料(物化劳动)与活劳动之间具有替代性的生产函数(Wolff，1979；Roemer，1981)。

目前，国内借助马克思主义最优经济增长理论开展研究的文献并不多见，其中乔晓楠和何自力(2016)以此为基础对工业化问题进行了探讨，乔晓楠等(2018)还结合劳动生产率与全劳动生产率对中国转换经济增长动能以及实现第二个一百年目标的条件进行了模拟分析。本文则试图建立一个马克思主义RBC模型来考察经济波动与经济结构调整。与 本文研究思路最为接近的文献为形岡 与金江的研究( 形 岡，2007；金江、形岡，2010；金江，2013)。本文与其的共同点在于都将社会再生产结构纳入分析，并且分别考察两大部类技术冲击的影响。不同点则包括以下五个方面:第一，岡形 与金江的研究建立在“集中经济”模型之上，而本文将基于“分权经济”模型开展分析。第二，由于基于“集中经济”模型， 岡所以形 与金江的研究没有区分工人与资本家两个阶级，并且也没有考虑剥削，而本文则纳入资本家对工人的剥削，并且在建模方式上也显著区别于山下(2005)的思路。第三，本文由于引入剥削，所以还将模拟分析不同劳资关系对经济波动的影响，而这样的分析在形岡 与金江的研究框架下是无法实现的。第四，形岡 与金江的研究对于第一部类生产的设定，仅使用活劳动，而不涉及物化劳动，本文则假设第一部类与第二部类一样，其生产均需采用物化劳动与活劳动，进而除了要分析劳动在两大部类中的配置比例，还需要对物化劳动的配置进行优化。第五，岡形 与金江的研究并未对价值层面的经济波动进行分析，而本文则分别对产出与价值两个层面进行模拟。

以上五个方面的不同点也将构成本文的创新之处。此外，马克思主义RBC模型与西方经济学RBC模型相比，由于理论基础不同也将存在显著差异，对此本文将在下一部分详细说明。

三、模型及其说明

（一）模型设定

假设存在工人与资本家两类代表性行为者以及两大部类的代表性企业。其中，工人通过提供劳动来获得收入，进而满足个人消费。考虑到跨期消费，工人会自主决策消费量，将储蓄提供给资本家，并获得利息收入。资本家由于拥有大部分生产资料，即存量资本品，因此能够以此作为抵押物获得贷款融资，并支付利息。获得贷款后的资本家按照特定的比例投资于两大部类企业。两大部类均需要利用生产资料与劳动相结合进行生产，但是由于两大部类的产品存在差异，因此各自的生产技术不同。假设企业作为生产主体面临着市场竞争，而资本家凭着占有生产资料而剥削工人在剩余劳动时间创造的价值。这意味着本文假设资本家虽然自身拥有劳动能力，却并不依靠提供劳动来获得收入。由于资本家可以决定整个经济系统的生产资料积累进程，所以在收入分配环节中占据更为强势的地位，进而剥削工人。换言之，本文与西方经济学的差异体现为生产资料与劳动的回报并非按照各自边际产出贡献来确定，而是要受到外生的劳资关系的影响。无论是工人还是资本家，都是凭借收入进行消费，进而最大化个人各期消费带来的商品有用性。需要注意的是工人与资本家消费的商品都是第二部类生产的消费品，而第一部类生产的资本品仅作为生产资料积累之用。

1.工人。假设在时期t，工人的数量为Nt。每个工人在时期t可以提供的劳动量为mt。工人的劳动量以劳动时间来计量，并且忽略不同工人之间的劳动差异，即将上述劳动时间理解为社会必要劳动时间。分别以cwt和swt来表示时期t工人的消费数量与储蓄量。其中，cwt以使用价值的实物量计量，即消费商品的数量，而swt为货币值，即储蓄的货币金额，至于特定储蓄量的购买力则还要考虑价格的变化。以rit表示通过单位储蓄可获得的利息。为了引入剥削，需要把工人的全部劳动时间区分为必要劳动时间lV与剩余劳动时间lM，并令w表示单位劳动时间创造的货币增加值①需要注意的是，w并非马克思主义政治经济学中的工资。这是因为如果资本家剥削工人，那么全部劳动时间所实现的货币增加值将不会全部成为工人的工资，其中的一部分将被资本家占有，所以w不是资本家支付给工人单位劳动时间的工资。。如果不存在剥削，工人将依据其投入的全部劳动时间l而获得自己的收入wl。然而，如果存在剥削，工人则仅能依据其必要劳动时间而获得收入wlV。此时，如果暂时抛开劳动价值论以及剩余价值理论，那么对于工人而言，其可能会产生以下幻觉，即单位劳动时间内的工资为w'=wlV/l，劳动时间为l，于是其收入为w'l=wlV。这里可以将w'姑且称为“幻觉工资”，其显然具有很大的迷惑性，便于掩盖资本主义制度下资本对工人的剥削。与此相对，剩余劳动时间的回报wlM将转化为利润，进而被资本家占有。此时，定义lV/l=σ且lM/l=1-σ，显然σ刻画了劳资之间的分配关系。因为有M/V=(1-σ)/σ或者σ=1/(1+M/V)，且由劳动量衡量的全部新增价值与以劳动所创造的货币增加值等比例变化②因为劳动的供给量为m，所以用劳动量衡量的商品全部新增价值即m，而劳动创造的货币增加值为wm，所以二者为等比例变化关系。，所以外生设定剩余价值率M/V等同于外生设定σ。于是可以将工人的行为选择刻画为以下最优化问题。

公式(1)为工人的目标函数与约束条件。目标函数为各期福利的折现值，每期的福利包括两个部分。其一是工人从消费中获得的商品有用性，为自然对数形式①类似的设定常见于马克思主义最优经济增长理论。。正如马克思所讲:“商品首先是一个外界的对象，一个靠自己的属性来满足人的某种需要的物。”②马克思的《资本论》(第1卷)(北京:人民出版社，1972:47)。其二是劳动供给对福利的负面影响，以幂函数刻画。马克思强调:“人在一个24小时的自然日内只能支出一定量的生命力。……这种力每天必须有一部分时间休息、睡觉，人还必须有一部分时间满足身体的其他需要，如吃饭、盥洗、穿衣等等。”③马克思的《资本论》(第1卷)(北京:人民出版社，1972:259-260)。因此，过多的劳动供给将对劳动力再生产构成负面影响。公式(1)中，βw为折现因子，γ为劳动时间供给弹性，φ为权重系数。工人将通过选择消费与储蓄进而最优化上述目标。工人面临的约束条件可以理解为当期的支出与收入相等。在支出方面，包括当期的消费与储蓄，其中消费品的价格被标准化为1。在收入方面，包括当期的劳动收入与上一期储蓄返还的本金以及利息。马克思认为资本家付给工人的工资包括三个部分，即维持工人自己生活的费用和维持工人家庭生活的费用以及必要的教育培训费用，简言之即工资要保证劳动力得以被“再生产”。除此之外，在工人创造的全部价值中到底有多大的比例作为工资付给工人，还受到阶级关系、工会作用等因素的影响。因此，本文利用σ反映劳资关系，并将其作为外生参数④很多马克思主义政治经济学研究，或者后凯恩斯主义经济学研究，都采用类似的外生分配关系设定。。于是，存在剥削的情况下，工人通过单位劳动仅能获得σwt。

通过求解上述最优化问题，容易得到关于工人消费的欧拉方程。公式(2)说明工人的跨期消费选择主要受到时间偏好与储蓄利率的影响。公式(3)说明工人的劳动时间供给由当期的消费与所得的劳动收入决定。

补充说明两点:第一，工人之所以需要出卖劳动力商品，其原因在于工人丧失了生产资料，进而供给劳动才成了唯一的收入来源。第二，工人的储蓄仅是一种跨期消费选择的结果，即当期储蓄、未来消费，这显然不以积累生产资料为目的，即储蓄无法改变工人被剥削的地位。

2.资本家。假设资本家数量与工人数量的比例为η，并且该比例在各个时期保持不变。于是，可知资本家数量为ηNt，且0＜η＜1。令kt和pt分别表示时期t的全部生产资料资本品存量及其单位价格。由于已经将消费品价格设定为1，所以tp可以理解为t期资本品与消费品的相对价格。分别以cct、ict和bct表示时期t资本家的消费、投资与贷款。其中，cct和ict以实物量计量，而bct为货币值。δ为折旧率，0＜δ＜1。由于资本家拥有更多的资本品，即生产资料，所以能够通过抵押获得贷款。假设一定时期内资本品的货币值中，比例为φ的部分是资本家通过贷款实现的投资，0＜φ＜1。此处的φ可以理解为杠杆率，且为外生参数。rbt表示利用单位贷款需要支付的利息，以rt表示单位生产资料(资本品)因转移自身价值而形成的货币价值，以(1- )σtl表示每个资本家无偿占有的劳动量，于是可以将资本家的行为描述为公式(4)。

公式(4)给出了资本家各期福利的折现值，由于资本家不依靠提供劳动获得收入，所以目标函数中不涉及劳动时间投入的抉择，βc为折现因子。资本家将通过消费、贷款以及生产资料积累决策，最优化上述目标。资本家面临的约束条件同样为当期的收支平衡。在支出方面，包括当期的消费和生产资料积累以及上一期贷款所需要支付的本息。在收入方面，包括全部的资本品收入(该部分回报用来补偿再生产过程中消耗掉的生产资料)、剥削收入以及当期获得的全部贷款。

通过求解上述最优化问题得到关于资本家消费的欧拉方程。公式(5)说明资本家跨期消费的选择受到时间偏好与贷款利率的影响，同时也反映出单位生产资料(资本品)因转移自身价值而形成的货币价值与贷款利率的关系，且受到资本品价格变动影响。

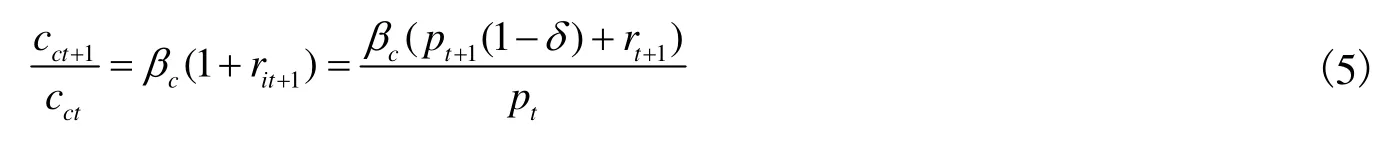
补充说明两点:第一，资本家之所以可以不劳动是因为资本家私人占有生产资料，因此没有必要供给劳动，依靠剥削剩余价值即可获得收入。第二，资本家贷款主要是为了投资生产并增加生产资料的积累。出于简化模型的目的，本文没有考虑借贷资本与银行资本。

3.两大部类及其企业。全部劳动产品划分为生产资料与消费资料两大类。其中，生产资料为“必须进入或至少能够进入生产消费的形式的商品”；消费资料为“进入资本家阶级和工人阶级的个人消费的形式的商品”①马克思的《资本论》(第2卷)(北京:人民出版社，1972:438-439)。。消费资料即最终消费品，由第二部类生产。生产资料则由第一部类生产，其本质是一种作为中间投入的资本品，它可以投入到第二部类之中，与劳动结合共同完成最终消费品的生产，进而使得生产链条被延伸，生产效率得以提高，并具有了迂回生产的性质。为了简化分析，令两大部类各自的全部企业数量与资本家的数量相等。假设两大部类代表性企业的生产函数为公式(6)。需要注意的是这里的生产函数与西方经济学的生产函数不同。此处的生产函数中投入的不再是生产要素，而是生产资料和劳动时间。生产资料本身也是劳动产品，即由劳动创造，因此是一种物化劳动，即往期的劳动凝结在生产资料之中。其中，yjt、Ajt、kjt和ljt分别表示时期t两大部类企业的产出量、技术水平、作为生产资料投入的资本品存量与劳动时间投入量，αj为资本品存量的产出弹性。j=1,2表示两大部类。在充分竞争的条件下，可得公式(7)和公式(8)①对于生产系统的设定，本文承袭了山下和大西(2002)以及大西和山下(2002)的思路，类似的设定还可以参见Dufourt等(2015)的文献。。对于以上两个公式，再次强调wjt表示单位劳动所创造的货币增加值，而并非工资。rjt表示单位生产资料由于其自身价值转移至新产品之中为了弥补投入损耗而获得的货币补偿，换言之即单位生产资料形成的货币价值。二者分别乘以劳动和生产资料投入量并加总则正好构成全部产品的销售额，进而使得全部产品所实现的收入被完全分配，参见公式(9)。

当然，由于生产资料被资本家私人占有，所以最终分配结构将不同于西方经济学与“三位一体公式”。按照西方经济学的逻辑，工人群体将得到wl，而资本家得到rk。按照政治经济学的逻辑，工人群体得到σwl，而资本家得到rk+(1-σ)wl。二者的区别就在于是按照边际产出贡献分配，还是考虑资本家对工人的剥削。由于本文基于政治经济学进行考察，因此分配关系属于后者。此外，这样的设定也与大西(2015)的研究显著不同。他指出:“r中包含着马克思称之为‘不变资本C’和‘剩余价值M’的两个部分。”②大西広 的《マ ルクス経 済学》(第2版)(東京:慶応義塾大学出版会，2015:136)。但是，本文认为r仅包含一个部分C，而M则通过剥削劳动取得(1-σ)wl。

4.市场均衡。上述模型涉及4个市场，即信贷市场、劳动力市场以及两大部类产品市场。信贷市场的均衡条件为公式(10)，即总储蓄等于总贷款。资本品均衡市场的均衡条件为公式(11)，即第一部类生产的全部资本品都转化为投资。公式(12)给出了资本品积累的动态方程，其中全部的资本品存量分别以vkt和1-vkt的比例被配置于两大部类企业之中。劳动力市场的均衡条件为公式(13)，其中全部的劳动分别以vlt和1-vlt的比例被配置于两大部类企业之中。由于充分竞争，所以均衡时公式(7)和公式(8)将得以满足。第二部类产品市场的均衡条件为公式(14)，即工人与资本家的消费总额等于第二部类生产的消费品总和。正如马克思所讲:“供求还以不同的阶级和阶层的存在为前提，这些阶级和阶层在自己中间分配社会的总收入，把它当作收入来消费，因此形成那种由收入形成的需求；另一方面，为了理解那种由生产者自身互相形成的供求，就需要弄清资本主义生产过程的全貌。”①马克思的《资本论》(第3卷)(北京:人民出版社，1972:217-218)。

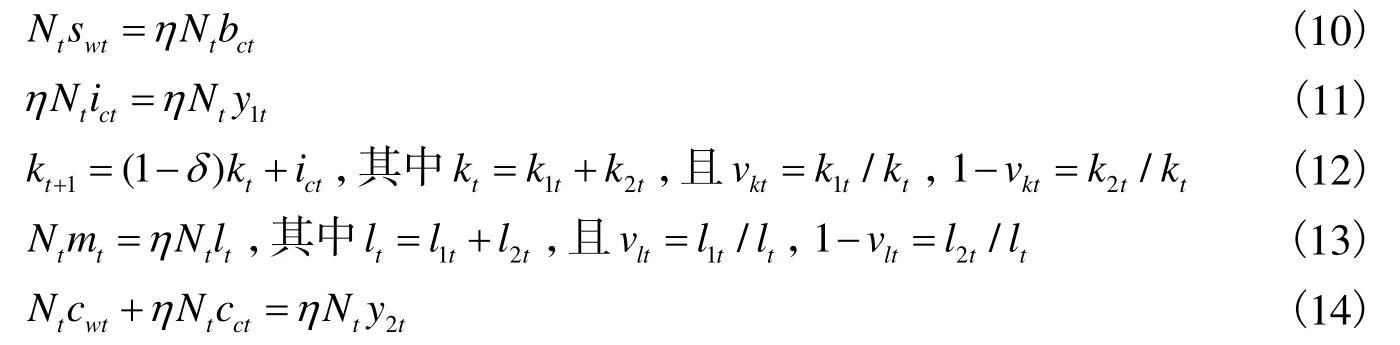
5.价值体系。马克思主义政治经济学以劳动量来计量价值，因此对于价值体系的考察首先要求解两大部类单位产品的价值量xj，且j=1,2，求解方法由方程组(15)给出。其中，表示资本品存量的跨期变化。这符合马克思的以下论述，即社会总资本的运动“不仅是价值补偿，而且是物质补偿，因而既要受社会产品的价值组成部分相互之间的比例的制约，又要受它们的使用价值和它们的物质形式的制约。”②马克思的《资本论》(第2卷)(北京:人民出版社，1972:437-438)。并且，解出的价值量xj，显然不是“个别价值”，而是“平均化为一个社会价值”，具有“市场价值”的特征③马克思的《资本论》(第3卷)(北京:人民出版社，1972:201)。。

于是，可以获得表1，即社会再生产中不变资本、可变资本与剩余价值的结构。这与金江(2011)的研究类似，但是在划分可变资本与剩余价值方面存在差异。

在马克思主义政治经济学中，资本有机构成与利润率非常重要，即从价值层面反映资本与劳动之间的比例关系，参见公式(16)和公式(17)。

表1 社会再生产的价值结构

6.随机冲击。假设外生冲击Zt均为一阶自回归过程AR(1)，其中，0＜ρZ＜1，εZt独立同分布且服从N(0,ω2)，参见公式(18)。本文主要考虑两大部类的生产技术冲击。

（二）模型说明

观察上述模型，似乎与建立在西方经济学之上的数理模型非常类似，但是其理论基础为马克思主义政治经济学。对此，进一步做出以下几点说明。

1.关于消费与商品的使用价值。商品具有使用价值与价值二因素。其中，价值以无差别的人类劳动计量，并且在交换过程中体现了彼此之间的交换关系。生产者追求的是价值实现，而并非使用价值。但是，商品又必须具备使用价值，即可以满足消费者对其有用性的要求，否则就没有人愿意通过交换来获得这种商品，进而生产者也就无法实现其价值。因此使用价值是消费者的目标，同时也是交换价值的物质承担者。在本文模型中，对于目标函数的设定，即遵循了上述观点，令工人与资本家的目标均为自身可以得到消费品有用性的函数。特别是对于工人而言，必要的消费是保障劳动力得以再生产的前提。

2.关于两大部类与迂回生产。两大部类的划分是马克思主义政治经济学的一个重要创新，其目的在于考察社会再生产过程中部门之间的比例关系，并且其中还蕴含了迂回生产的思想。最终用来满足人类社会需要的是消费品，但是消费品的获取至少可以有两种不同的途径。第一，将社会全部劳动安排到第二部类的生产之中，由这些劳动直接生产消费品。第二，先将一部分劳动安排在第一部类中，并运用这些劳动创造出资本品，即物化劳动，然后再让资本品与其余的劳动结合，共同创造出消费品。两种途径相比较，前者更为直接，而后者则延伸了生产链条，具有迂回生产的性质。那么，如何在不同的生产途径中进行抉择呢？关键在于生产效率。因为在劳动总量不变的条件下，如果给定不同部类生产的技术水平，那么总会存在一个最优的劳动分配比例，按照该比例将社会全部劳动分别配置到两大部类之中，则可以实现最大化的最终消费品产出量。从历史唯物主义的角度出发，工业革命的爆发，导致生产从手工劳动到机器大工业的变革，正体现了迂回生产的特征。因为以机器替代劳动可以突破人类劳动在力量、精度以及持久性方面的限制，但是机器同样需要先期劳动的投入才可以获得。于是，基于以上分析，三个结论至关重要。第一，通过迂回生产，积累必要的资本品，可以在动态过程中不断提高生产效率。第二，资本品积累的过程直接影响到社会总劳动各个时期如何在两大部类之间进行配置。第三，无论是资本品还是消费品，都由劳动创造，因此它们都可以被还原为不同时期的劳动。本文模型的设定就体现了上述思想，其中资本家的生产资料积累支出决定了资本品的需求量。

3.关于资本品与资本。理解本文模型与西方经济学模型的区别，需要辨析以下三个概念，即马克思主义政治经济学中的“资本品”与“资本”以及西方经济学中的“资本”。第一，在马克思主义政治经济学中，“资本品”与“资本”不同。“资本品”是第一部类的劳动产品，是技术进步导致迂回生产的产物。“资本”则体现了生产关系，其功能是获得价值的增值。只有当“资本品”被资本家私人占有，并以此来无偿占有工人的剩余价值，此时的“资本品”才具有“资本”的属性。第二，马克思主义政治经济学中的“资本”与西方经济学中的“资本”不同。前者蕴含了生产关系，后者则仅是一种生产要素。第三，马克思主义政治经济学中的“资本品”与西方经济学中的“资本”不同。二者虽然都与劳动结合进行生产，而前者却是作为迂回生产中的一个组成部分，并且可以被还原为劳动，后者却与劳动并列。

4.关于社会再生产。马克思主义政治经济学对社会再生产过程进行了深入剖析，进而给出可以维系再生产过程的比例关系。这与本文模型两大部类的市场出清条件相吻合。简单再生产的实现条件要求，即模型在稳态均衡下的

5.关于剥削。众所周知，在西方经济学中不存在“剥削”这一概念，各种要素被投入生产之中，按照其边际产品的价格获得各自的回报，因此完全竞争条件下企业只能获得零利润。这也正是“三位一体公式”的错误根源。马克思主义政治经济学则认为价值是由劳动创造的，生产过程中不变资本仅是转移其自身价值，而劳动才会带来价值增值，即创造出新价值。但是，由于资本家对生产资料的占有，其可以无偿获得工人在剩余劳动时间创造的价值。并且，这个剩余价值也正是利润的来源。上述分配关系就是所谓的“剥削”。虽然本文模型的设定参考了马克思主义最优增长理论的思路，但是在“剥削”的设置上则与其存在明显的差异。山下(2005)的研究假设资本家与工人各自所拥有的资本品存量存在差异，且前者要大于后者。如果资本家把自己的一部分资本品以借贷形式交由工人使用，则可以提高工人的产出。但是，资本家占有了工人产出增加的部分，进而形成剥削。此外，如前文所述，本文的模型设定也与大西(2015)的研究存在着差异。本文模型强调资本家并不提供劳动，因而也就不会获得自身劳动的所得，同时假定劳动创造的货币增加值并不完全归工人所有，其中的一部分被资本家无偿占有，进而形成剥削。另外，工人由于跨期消费选择形成的储蓄可以借贷给资本家。因此，关于剥削的模型设定，本文既不同于西方经济学，也不同于马克思主义最优经济增长理论。

6.关于利润率平均化。本文假设两大部类企业的数量相同，并且为了简化分析，也与资本家数量相同①资本家与企业数量不同也不会实质性影响本文的分析结论。。每个资本家都投资于两大部类的企业，即相当于决定一个投资组合。由于资本家可以无偿占有一部分工人劳动创造的剩余价值，所以马克思所讲的“利润”也来源于这部分剩余劳动时间内所实现的货币增加值。马克思主义政治经济学的利润率由定义。由于本文以代表性资本家进行分析，所以每个资本家所选择的投资组合都相同。这也就意味着由所确定的利润率即为平均利润率。于是，等量资本将获得等量利润②注意“等量资本”的“资本”与“等量利润”的“利润”都是马克思主义政治经济学的概念，需要与西方经济学概念加以区分。。这显然是一种简化的处理，即用投资组合的方式实现了利润率平均化，未来可以进一步探讨特定资本家仅投资某一部类的情况。但是本文所采用的方法将能够为解决等量资本获得等量利润、价值转化为生产价格提供一种不同于以往的思路。

7.关于市场出清。马克思主义政治经济学既对市场出清的情况进行了分析，又对市场没有出清的情况进行了研究。前者可以参见对社会再生产的讨论，特别是两大部类的平衡关系就是典型的例子。并且，一旦社会再生产过程不能满足上述平衡关系，则会出现由比例失调导致的经济危机。后者当然更是马克思主义政治经济学研究的重点，否则就不会有“生产过剩”这样的概念出现，而劳动力市场无法出清即失业，这将成为“产业后备军”的一个基础。此外，西方经济学也可以分别考察市场出清与市场不出清的情况。特别是秉承了凯恩斯主义经济学传统的一类模型就放弃了市场出清的假设，而从价格粘性等角度加以研究。但是，需要注意的是这显然与马克思主义政治经济学对市场无法出清原因的解释有所不同。本文的模型沿用了市场出清假设，如此处理更接近于马克思主义政治经济学中的“基准状态”(Benchmark)，当然也更加适应分析社会再生产的比例关系，并且未来还可以进一步纳入非市场出清假设进行深入考察。

8.关于劳动与经济增长。根据“劳动价值论”，劳动是价值的源泉。显然，没有劳动就无法创造出各种产品，进而也就无法提升社会财富。因此，如果针对本文模型进行稳态求解，也不难发现产出量与价值量均为劳动投入量的增函数。这也与“劳动价值论”相互契合。

四、对技术冲击的模拟分析

（一）对技术冲击的模拟设定

由于本文的研究目的是建模并分析经济波动中社会再生产结构的变化，并非对特定经济体的实际经济波动进行拟合，因此在参数设定上并没有采用贝叶斯估计进行校准，而直接参考相关研究的参数取值(陈昆亭等，2015；Wickens，2008)。具体的设定参见表2。需要说明的是对于两大部类生产涉及的外生参数，Liu(2010)和Shen(2011)分别进行过估计，二者在基础模型、估计方法、采用数据与研究结论等方面均存在差异，但共性特征是第一部类中劳动产出弹性都要显著低于第二部类，而本文参数取值保留了该特征。此处采用确定模拟方式，分别对两大部类生产技术冲击进行模拟，并将稳态解作为初始值。

表2 参数校准值

（二）生产技术冲击的影响

对第一部类生产技术施加0.01正向冲击，图1给出了劳动配置与单位产品所包含价值量的动态调整过程。观察活劳动配置情况，由于第一部类发生技术进步，因此将更多的活劳动配置于第一部类将更加有利于整体效率的提升。与之相对的则是第二部类的活劳动配置比例将相应减少。与活劳动的配置情况类似，物化劳动形式的存量资本品在第一部类的配置比例也受到该部类技术进步的影响而提升，而在第二部类的配置比例相应下降。两大部类单位产品所包含的价值量，受到第一部类技术进步的影响，均有所下降。并且，第一部类产品价值量的降幅更大，且收敛得更快。

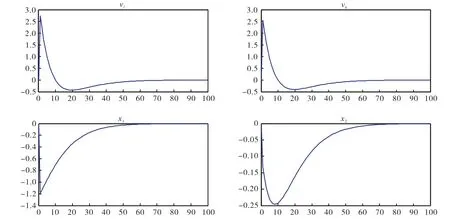
图1 第一部类生产技术冲击对劳动配置与单位产品价值量的影响

图2给出了经济系统在第一部类正向技术冲击下的动态调整过程。第一，从两大部类的产出来看，第一部类产出先升后降，之后收敛于稳态，而第二部类的产出先降后升，并超过稳态水平，之后再逐步收敛。这是由于初期受到第一部类技术进步影响，劳动更多地被配置到更有效率的第一部类，导致第一部类产出增加，而第二部类产出下降，随着第一部类产出更多的资本品促进了积累，且被应用于第二部类生产，又将导致第二部类产出超过稳态水平。最终随着技术冲击消退，两大部类产出先后收敛于稳态。以价格加权得到的总产出则受到上述两大部类产出变化的影响呈现出先升后降的特点。第二，从劳动供给及其配置来看，第一部类的技术进步促进劳动供给增加，并且在提高第一部类配置比例的同时，降低第二部类劳动配置数量，并逐步收敛。从存量资本品的变化与配置来看，其变化特点与活劳动类似，不过时期上相对滞后，这是由于活劳动是生产的基础与创造新价值的源泉，资本品也是劳动的产物。因此，资本品的变化要相对滞后于活劳动的变化。第三，从消费来看，工人消费先降后升，之后超过稳态水平，再逐渐收敛，而资本家消费则先升后降，且基本高于稳态水平。其原因在于第一部类生产技术进步有利于资本品积累，而资本家受此影响则更倾向于向工人借贷，进而初期抑制了工人消费，但是随着资本积累增加有利于扩大消费品产出，进而增加了工人消费。对于资本家而言，资本积累增加有利于提高收入，而消费品产出增加也有利于扩大消费，因此其消费量呈现出正向波动。由于工人的人数更多，所以总消费的波动特点更加接近于工人消费波动的特征。第四，从价格体系来看，劳动的货币增加值出现正向波动，而资本品回报出现负向波动，第一部类产品较之于第二部类产品的相对价格则出现负向波动。这与第一部类生产效率提高之后第一部类产品稀缺性降低有关。

图2 第一部类生产技术冲击对经济系统的影响

图3给出了经济系统在第一部类正向技术冲击下其价值层面的动态调整过程。第一，观察价值量。第一部类虽然单位产品包含的价值量出现负向波动，但是由于其产出出现正向波动，且波动幅度更大，因此第一部类产出的价值量也呈现正向波动特征。第二部类的情况与第一部类相反，受到第一部类技术进步的影响，其价值量呈现负向波动特征。由于第一部类的正向波动幅度大于第二部类负向波动的幅度，所以经济系统的总价值量也呈现出正向波动特征。第二，观察资本有机构成。无论是第一部类、第二部类，还是经济系统总体的资本有机构成，均出现先降后升——超过稳态水平——再逐步收敛的特点。这与资本品包含的价值量出现负向波动有关，虽然劳动供给与资本品存量都增长了，但是由于单位资本品价值量在初期下降，所以依然导致资本有机构成在初期下降。第三，观察利润率。此部分模拟给定了由劳资关系系数确定的剩余价值率，因为利润率等于剩余价值率除以资本有机构成加上常数1的和，所以当剩余价值率不变，且资本有机构成下降时，显然利润率会提高。因此，两大部类以及经济系统总体的利润率与其各自的资本有机构成变化特征相反。

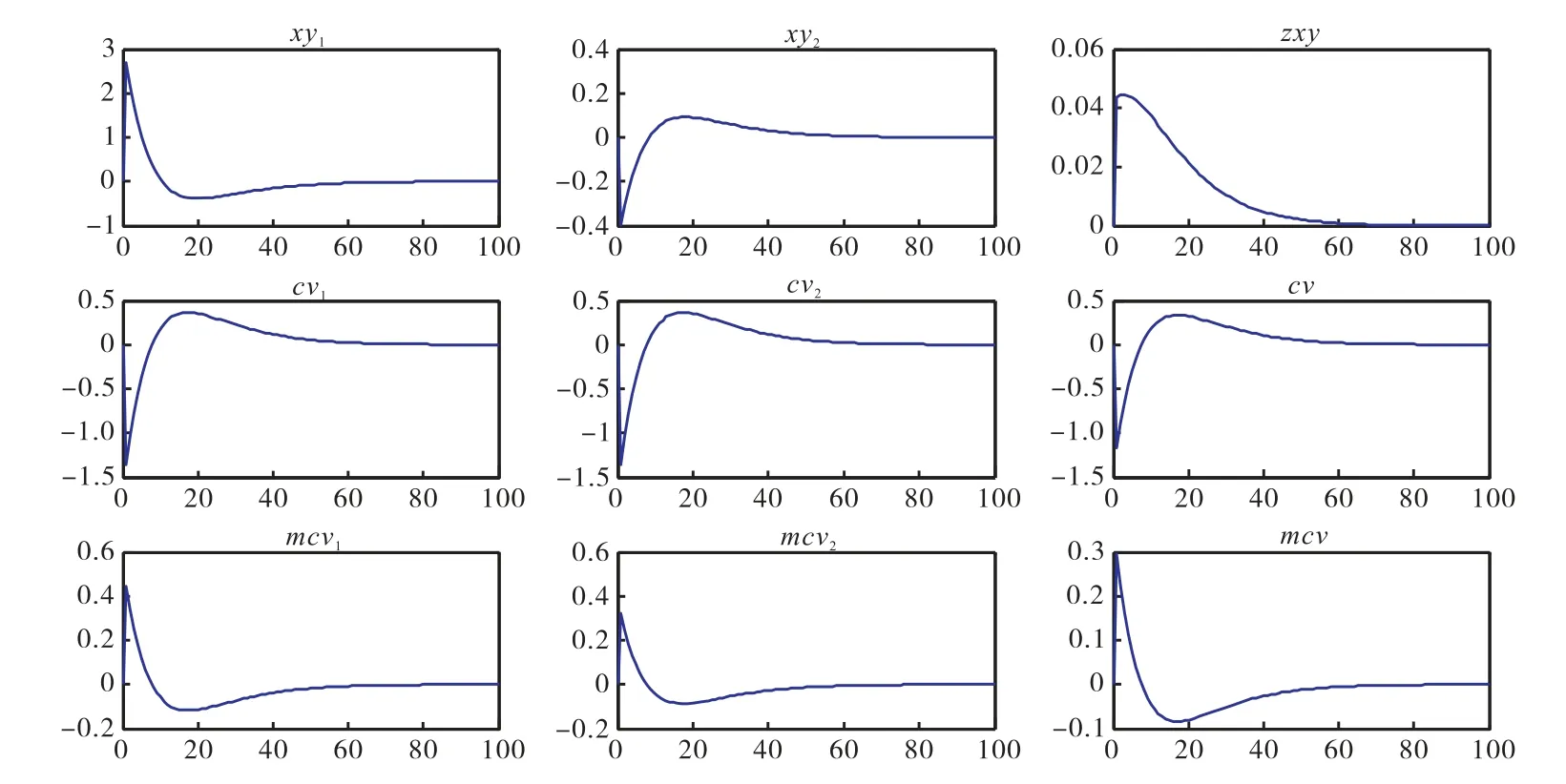
图3 第一部类生产技术冲击对价值系统的影响

当然，也可针对第二部类生产技术施加0.01正向冲击，并模拟分析其影响下的资源配置、单位产品所包含价值量、经济系统以及价值系统的动态调整过程。鉴于篇幅所限，本文不再给出具体的模拟结果及其经济机制分析，仅在结论部分进行报告①感兴趣的读者可以扫描本文二维码点击“附录”获取。。

五、对劳资关系的模拟分析

（一）对劳资关系的模拟设定

在考察了两大部类技术冲击导致的经济波动之后，接下来分析劳资关系变化对经济波动的影响。本部分采用随机模拟方式，同时引入两大部类的技术冲击，然后比较不同劳资关系情境下的模拟结果。本文反映劳资关系的参数为外生给定，其决定了工人通过劳动创造的全部货币增加值中分别归属工人与资本家的份额比例，进而由此决定剩余价值率。针对不同的劳资关系，本文将进行方差分解的比较，并且考察经济系统在波动性(volatility)、协动性(comovement)以及粘持性(persistence)方面的差异②此处参考了Stock和Watson(1999)对模拟结果的分析思路，但也有所差异。。

（二）劳资关系与方差分解

表3给出了同时引入两大部类技术冲击后各个经济变量波动的方差分解结果。整体来看，可将各个变量划分为三种类型。第一类变量的波动仅受到第一部类技术冲击的影响，而没有受到第二部类技术冲击的影响，因此无论劳资关系如何变动，都不影响方差分解的结果。这类变量包括刻画产出与劳动配置层面的大部分变量以及刻画价值层面的全部变量。由于第一部类的生产不以第二部类的产出作为中间产品，所以y1显然仅受到第一部类技术冲击的影响。此外，劳动和作为生产资料的资本品的配置结构也属于这种类型。如果计算上述变量的稳态解可发现，其并非第二部类技术参数的函数。由于劳资关系外生设定并可以满足劳动力再生产的要求，所以资本有机构成与利润率仅受到第一部类技术冲击的影响。第二类变量的波动是随着σ的增加，第一部类技术冲击的影响增大，而第二部类技术冲击的影响减小。这种类型的变量包括y2和x2以及刻画价格体系的变量。由于劳资关系改善，劳动供给将增加，而第二部类的产出、价值以及消费都受到第一部类中间投入的影响，因此劳动供给的增加将放大第一部类技术进步的影响，相应第二部类技术进步影响降低。第三类变量的波动特点与第二类变量正好相反，随着σ的增加，第一部类技术冲击的影响减小，而第二部类技术冲击的影响增大。cw就属于这类变量，其可以与cc对应起来分析。二者变化的特征说明随着劳资关系的改善，工人收入对于资本品对产出贡献的敏感性弱化，进而导致第一部类技术冲击的影响降低，相反资本家收入则对资本品对产出贡献的敏感性加强，进而导致其更加依赖第一部类的技术进步。

表3 劳资关系变化与两类技术冲击的方差分解(%)

（三）劳资关系与经济波动的波动性

表4给出了同时引入两大部类技术冲击后各个经济变量在不同σ取值下标准差的比值，通过该指标就可以分析出劳资关系变化对各个变量波动性的影响。本文以作为基准，显然该指标大于1时，意味着波动性加大，反之则说明波动性降低。各个变量可以划分为两种类型。第一类变量随着σ的增加，波动幅度不断增大，包括y1、y2、l1、l2、k1、k2、w、r、p、cw、x1、x2、xy1、xy2。第二类变量随着σ的增加，波动幅度不断减小，包括cc、cv1、cv2、cv、mcv1、mcv2、mcv。由此可以获得的以下结论:第一，劳资关系对于两大部类产出量波动与价值量波动的影响方向一致，但是产出量波动幅度所受到的影响更大。第二，劳资关系对两大部类产品的相对价格波动与各自产品所包含的价值量波动的影响方向也一致，且波动幅度也大体相等。第三，劳资关系对资本有机构成波动与利润率波动的影响方向一致，且利润率波动幅度显著大于资本有机构成的波动幅度。第四，劳资关系对价值量(单位产品价值量与部类价值总量)与价值比例(资本有机构成与利润率)的影响方向相反。

表4 劳资关系对经济波动波动性的影响

（四）劳资关系与经济波动的协动性

表5给出了同时引入两大部类技术冲击后在不同σ取值下的不同变量之间的相关系数，通过该指标就可以分析出劳资关系变化对各个变量协动性的影响。显然，相关系数的符号刻画了正相关或者负相关，相关系数的绝对值则刻画了协动程度。不同变量组合可以划分为七种类型。第一类变量组合呈现正相关，且随着σ的增加协动程度提高，包括(l1，y1)、(k1，y1)、(k2，y2)、(l，k)、(cw，cc)、(x1，x2)、(k，cv)。第二类变量组合也呈现正相关，且随着σ的增加协动程度降低，包括(l，mcv)。第三类变量组合还呈现正相关，且随着σ的增加其协动程度先降后升，包括(l2，y2)。第四类变量组合呈现负相关，且随着σ的增加协动程度提高，包括(k2，x2)、(k，mcv)。第五类变量组合呈现负相关，且随着σ的增加协动程度降低，包括(l，cw)、(l1，x1)、(k1，x1)、(l，cv)。第六类变量组合随着σ的增加呈现出由正相关转变为负相关的特征，包括(y1，y2)、(l，cc)。第七类变量组合则随着σ的增加呈现出由负相关转变为正相关的特征，包括(l2，x2)。

表5 劳资关系对经济波动协动性的影响

（五）劳资关系与经济波动的粘持性

表6给出了同时引入两大部类技术冲击后各个经济变量在不同σ取值下的一阶自相关系数，通过该指标就可以分析出劳资关系变化对各个变量粘持性的影响。显然，自相系数增加意味着粘持性增大，反之则粘持性减小。各个变量可以划分为两种类型。第一类变量随着σ的增加粘持性不断增大，包括w、r、p、cw、cc、x1、x2、cv1、cv2、cv、mcv1、mcv2、mcv。第二类变量随着σ的增加粘持性不断减小，包括y1、y2、l1、l2、k1、k2、xy1、xy2。由此可以获得的以下结论:第一，劳资关系对于两大部类产出量粘持性与价值量粘持性的影响方向一致，但是产出量受到的自相关影响程度更大。第二，劳资关系对两大部类产品的相对价格粘持性与各自产品包含价值量粘持性的影响方向也一致，且自相关程度大体相等。第三，劳资关系对资本有机构成粘持性与利润率粘持性的影响方向一致，且自相关程度也大体相等。第四，劳资关系对单位产品价值量以及价值比例(资本有机构成与利润率)与部类价值总量粘持性的影响方向相反。

表6 劳资关系对经济波动粘持性的影响

六、结论与展望

本文在吸收借鉴马克思主义最优经济增长理论的基础上，构建了一个马克思主义政治经济学数理模型，并以此对经济波动中社会再生产的比例结构调整过程进行了考察。概括而言，结论包括以下四个方面。第一，分别引入两大部类技术冲击并比较经济波动特征，可以发现其影响具有显著的差异。无论是第一部类还是第二部类，其技术进步都将引导劳动更多地配置于该部类之中，进而改变两大部类的产出量，并进一步引发社会再生产比例结构的变化。第二，同时引入相同程度的两大部类技术冲击，可以通过方差分解来测度不同经济变量波动受到两种技术冲击影响的差异。除了工人与资本家的消费量、第二部类产出与单位产品价值量以及劳动回报之外，其他变量的波动都更多地受到或者仅受到第一部类技术冲击的影响。第三，在同样程度的技术冲击之下，劳资关系的变化，即资本家对工人剥削程度的变化，将显著改变经济波动的波动性、协动性以及粘持性。单从两大部类的产出维度来看，剥削程度的降低，将影响工人的供给劳动，进而加剧经济波动，并降低其自相关程度。第四，由于本文的模型不仅可以对实物生产进行考察，而且还可以对以劳动时间计量的价值量变化进行分析。因此，通过比较则可以发现，两大部类单位产品的相对价格与其各自产品包含的价值量存在差异，并且两大部类各自的总产出与产品价值总量也存在差异。

从模型的形式上看，本文的模型与西方经济学的模型相比，作出了三点变化。其一是假设收入分配不依赖于投入的边际产出贡献，而与生产资料所有制相关，进而存在剥削。其二是将生产资料(资本品)与消费资料(消费品)区分，进而构建符合马克思主义政治经济学社会再生产理论的两大部类迂回生产链条。其三是在完成经济的物质体系求解之后，再结合劳动价值论，求解出两大部类单位商品所包含的价值量以及由此可以求得的资本有机构成等比例关系。虽然本文仅作出了三点建模变化，但是这已经可以将马克思主义政治经济学的理论特质在模型中勾勒出来。

毫无疑问，本文采用的模型还不够完善。例如，对生产过剩、产业后备军、货币与资本的转化及其循环过程都还尚未涉及。但是，本文提供了一个包含社会再生产结构、资本对劳动剥削关系以及区分使用价值与价值的基本分析框架。

因篇幅所限，本文仅利用模型对经济波动机制与特征进行了初步的模拟分析。未来深化研究的方向将主要集中在以下两个方面。从理论研究层面可以进一步引入宏观经济政策或者增加其他部门来丰富研究内容。从实证研究层面也可以基于该模型，通过参数的校准来模拟解释某个经济体的经济波动。