相亲结婚真的靠谱吗——基于CFPS2014数据的研究

叶金珍 王 勇

一、引 言

据中国民政部统计，截至2015年，中国单身成年人口已超过2亿，单身成年人约占总人口的14.6%。《2016—2017年中国男女婚恋观调研报告》显示，过去一年，受访者人群中，被父母逼过婚的男、女占比分别为56%和50%，而逼婚压力还在持续上升。随着剩男剩女的不断增加，春节“相亲潮”受到广泛关注。然而，相亲结婚真的靠谱吗？这可能是“每逢春节被相亲”的单身人士的共同心声。近年来，网络流传各种“反相亲攻略”、“反逼婚攻略”，那么，值得深思的是:自由恋爱式婚姻一定比相亲式婚姻更幸福、更长久吗？

相亲和自由恋爱的区别在于，结婚对象的选择方式不同:相亲的对象由他人选定，可选范围较小；而自由恋爱的对象范围更广。主流经济学认为，人的偏好具有多样性，选择项越多，效用越大。但这种观点仅适用于商品消费选择，能否适用于情感研究还有待进一步验证。不同于主流经济学，社会学领域较具有代表性的选择理论(选择悖论、选择超载理论)认为，太多的选择可能是件坏事，过多的选择可能会降低满足感(Schwartz，2014；Iyengar和Warburton，2011)。根据该理论，相亲式婚姻意味着，结婚对象的可供选择范围由父母或第三方指定，因而可选对象是有限的；自由恋爱式婚姻意味着，结婚对象的选择范围不受他人控制，所有认识或可能认识的异性都是可能的结婚对象；与其通过自由恋爱来寻找结婚对象，可能还不如在有限个相亲人选中选择结婚对象。该理论与日本的实际情况相符，据日本仲人联合会调查，自由恋爱式婚姻的离婚率在40%左右，相亲式婚姻的离婚率在10%左右；印度的数据也表明，相亲式婚姻的离婚率比自由恋爱式婚姻的离婚率低。

选择悖论为“相亲潮”的现实意义提供了一种解释，但多数年轻人抗拒相亲的一个重要原因在于，相亲式婚姻是否有爱情。Gupta和Singh(1982)的研究表明，在自由恋爱式婚姻中，爱情随时间推移出现一定程度下降；在相亲式婚姻中，爱情反而随时间上升；最终，相亲式婚姻中的夫妻甚至比自由恋爱式婚姻中的夫妻更加恩爱。Epstein等(2013)认为，相亲式婚姻的爱情是可以培养的，即所谓的“先结婚，后恋爱”，该结论与Gupta和Singh(1982)的结论一致。Epstein等(2013)的研究还表明，婚姻契约作为一种承诺，对于相亲式婚姻的爱情培养特别重要；同时，夫妻的相互扶持与同理心也有助于培养爱情，该观点和脆弱理论一致(Strong和Aron，2006；Arriaga等，2007)。

上述文献表明，相亲结婚的婚姻质量可能更高，相亲可能是靠谱的。但这些文献基本上都是从社会学角度进行研究的，少有文献从经济学角度进行理论或实证分析。相亲和自由恋爱，不仅仅是人生选择，同时也是2种婚姻匹配方法。Edlund和Lagerlof(2006)认为，相对于父母参与的相亲式婚姻，自由恋爱式婚姻允许年轻夫妻掌握彩礼的使用权，因而更有利于经济发展。Huang等(2012)运用中国数据进行实证研究，结果表明，自由恋爱式婚姻更和谐，相亲式婚姻的收入更高，由此提出，父母或第三方在帮忙寻找相亲对象时，更倾向于选择经济实力雄厚的对象，即倾向于用金钱来替代爱情。进一步地，Huang等(2016)建立婚姻匹配的理论模型，该模型将匹配方法分为自由恋爱和相亲(父母参与)，其研究发现，父母参与婚姻匹配的夫妻在婚后更加照顾父母，但这种孝顺是以牺牲夫妻和睦为代价的，这和Becker等(2016)的观点一致。

综上所述，尽管已有文献考察了婚姻匹配方法与夫妻和睦的关系(Huang等，2012；Huang等，2016)，遗憾的是，相亲结婚是否真的靠谱，婚姻匹配方法到底多大程度影响了婚姻质量，现有文献对此语焉不详，特别是，几乎没有文献运用经济学方法研究相亲与婚姻质量的关系。本文将从两个维度(婚姻满意度、婚姻稳定性)衡量婚姻质量，考察不同婚姻匹配方法对婚姻质量的影响，以弥补相关领域的研究空白。

二、理论模型

（一）基本设定

参考Huang等(2016)的模型基本框架(简称HM模型)，我们结合中国实际情况，修改了HM模型的部分设定，因而本文与HM模型在假设上有着相同和不同之处。相同之处表现为:(1)婚姻产出既包括经济(物质)产出也包含情感产出，两者均被纳入效用函数；(2)婚姻匹配方法分为两大类，即相亲和自由恋爱。不同之处主要体现为:(1)婚姻产出函数的投入要素为夫妻双方的特质，而不仅仅是人力资本变量；(2)情感产出系数由夫妻双方的特质共同决定，而非独立于某一方的特质；(3)相亲的介绍人是父母及父母相关的第三方，介绍人(媒人)是利他的；(4)成本函数主要指婚姻经营成本，而非搜寻成本。

（二）自由恋爱的最优匹配对象选择

以个体i的婚姻匹配为例，个体i为任一单身未婚男性(女性)，Xi是代表个体i特质的向量，则其可能的结婚对象j为任一单身未婚女性(男性)，Xj是代表个体j特质的向量。个体特质向量Xi、Xj包括外貌、身体、体重、谈吐、受教育年限、工作能力、社交能力和家境等。个体i的目标效用函数为:

其中，g（Xi,Xj）为个体i与个体j的婚姻物质产出。参数e为情感产出系数，可理解为匹配度或夫妻恩爱程度，e≥0，情感产出为e×g（Xi,Xj），它基于一定的物质基础，但e不完全依赖于物质，情感产出由夫妻恩爱程度和物质基础共同决定，若夫妻恩爱程度为0，则无论物质产出有多大，情感产出都为0。参数κi为物质分配系数，个体i从婚姻中获得的经济利益不可能超过婚姻的物质总产出，因而0 ≤κi≤1，个体i获得的物质产出为κi×g（Xi,Xj），其配偶(个体j)获得的物质产出为（1 -κi） ×g（Xi,Xj）；c（e,Xi,Xj）为婚姻经营成本，该成本为夫妻恩爱程度e、个体特质Xi、Xj的函数。

上式表明，情感产出系数为个体特质的函数，即夫妻恩爱程度由夫妻双方的特质共同决定。与物质产出不同的是，情感产出(情感上的满足感)可看作家庭内部的一种公共物品，且夫妻恩爱带来的情感满足感可超越物质本身带来的满足感，即e的取值可能大于1。夫妻越恩爱，个体i、j获得的情感满足感λ（Xi,Xj） ×g（Xi,Xj）越大。情感产出需要一定的物质基础，若物质产出g（Xi,Xj）等于0，则情感产出也为0。在已知自身特质Xi的条件下，个体选择最优匹配对象，将式(2)代入式(1)，对Xj求导:

令式(3)为0，可求得个体通过自由恋爱选择的最优匹配对象的特质。若个体i与特质为的对象结婚，则个体i获得的物质产出和情感产出分别为，同时付出的婚姻经营成本为

（三）相亲的最优匹配对象选择

当父母或第三方帮助个体寻找最优结婚对象时，他们仍然以最大化个体的效用为目标。值得一提的是，夫妻恩爱程度由当事人感知，相亲介绍人对当事人(个体、ij)的情感产出信息不甚了解，介绍人在缺少情感产出信息的条件下，最优化个体i的效用。此时，情感产出系数e看作未知的常数，式(1)对Xj求导得到:

令式(4)为0，可求得相亲的最优匹配对象j的特质。若个体i与特质为的对象j结婚，则个体i获得的物质产出和情感产出分别为，同时付出经营成本为

（四）自由恋爱还是相亲

若个体i与特质为的个体结婚，则个体i从婚姻中获得的效用为；若个体i与特质为的个体结婚，则个体i从婚姻中获得的效用为是在信息完全的条件下求得的最优解，是在情感产出信息缺失的条件下求得的效用最大化解即自由恋爱式婚姻的效用大于相亲式婚姻的效用。

进一步地，比较不同婚姻匹配方法的婚姻经营成本。自由恋爱式婚姻的经营成本为，相亲式婚姻的经营成本为，结合式(1)可知，若自由恋爱式婚姻的情感产出系数较高或物质产出较高，即使其婚姻的经营成本大于相亲式婚姻，其婚姻的效用也仍然大于相亲式婚姻。换言之，当自由恋爱式婚姻的维系成本更高时，仍然可能满足。由此可见，自由恋爱和相亲作为两种不同的婚姻匹配方法，各有利弊，尽管自由恋爱式婚姻可能更幸福，但其婚姻的经营成本高于相亲式婚姻，而过高的婚姻经营成本将增加婚姻解体的风险。综上，提出假说1和2。

假说1:当其他条件相同时，相对于相亲式婚姻，自由恋爱式婚姻有更高的婚姻满 意度。

假说2:当其他条件相同时，相对于自由恋爱式婚姻，相亲式婚姻有更高的稳定性。

三、基本回归分析

（一）基准模型

1.相亲与婚姻满意度

根据假说1，为验证同等条件下，相亲式婚姻的满意度是否低于恋爱式婚姻，模型设定为:

其中，因变量satifai表示个体i的婚姻满意度；meeti为是否相亲的二元变量，若夫妻两人通过相亲认识，则meeti取1，否则取0；Xi为一组影响婚姻满意度的控制变量，ε1i为扰动项。为了进一步控制个体差异，参考王智波和李长洪(2016)，外貌与婚姻竞争力相关，因此，引入个体的外貌变量作为婚姻竞争力的代理变量。同时，加入工作满意度以控制个体性格上的异质性，相关模型设定为:

其中，looki是外貌变量，worki表示工作满意度，其他变量的设定与式(5)相同。

2.相亲与婚姻稳定性

根据假说2，为验证相亲式婚姻是否更稳定，设定如下模型:

其中，因变量stablei表示个体i的婚姻稳定性，Zi为一组影响婚姻稳定性的控制变量，1μi表示扰动项，其他变量的设定与式(5)相同。为了进一步降低个体差异对婚姻稳定性的干扰，我们仍采用外貌变量作为婚姻竞争力的代理变量，同时，加入对陌生人的信任程度变量以控制个体性格上的异质性。设定的识别模型如下:

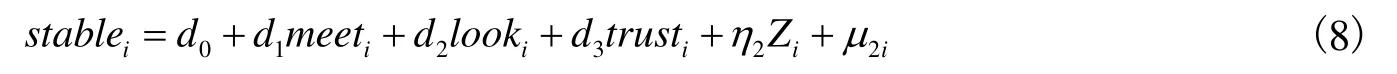
其中，trusti为信任度，其他变量的设定与式(7)相同。

（二）变量定义与基本估计方法

本文的数据来自中国家庭追踪调查(简称CFPS)2014年的成人调查问卷。CFPS是北京大学中国社会科学调查中心实施的一项全国性大规模社会跟踪调查项目，它采用多阶段分层(PPS)抽样方法。CFPS数据基本满足本文的数据需求，这主要体现在:(1)2014年的问卷首次设计了“婚姻满意度”的提问；(2)调查了受访者与当前配偶的认识方式；(3)包含受访者的外貌信息，但其他社会调查(例如CHNS)往往缺乏外貌数据。变量定义如下。

1.因变量

(1) CFPS数据将婚姻满意度分为5个等级，“1”表示非常不满意，“2”表示不满意，“3”表示一般满意，“4”表示满意，“5”表示非常满意。(2)本文用“是否离婚”作为婚姻稳定性的基准指标，若受访者为离婚状态，则取值为1，否则，取值为0。(3)为进一步检验回归结果的稳健性，我们还替换了因变量的衡量指标，用受访人“对自家生活的满意程度”作为婚姻满意度的代理变量。CFPS将自家生活满意度分为5个等级，从1到5代表的满意度依次上升。同时，用婚姻持续时间来衡量婚姻稳定性。

2.核心自变量(meeti)

本文通过夫妻双方的认识方式来定义相亲变量。CFPS就“与配偶/同伴如何认识”进行了提问，回答选项有10个，分别是:“1.在学校自己认识”“2.在工作场所自己认识”“3.在居住地自己认识”“4.在其他地方自己认识”“5.经亲戚介绍认识”“6.经朋友介绍认识”“7.经婚介介绍认识”“8.其他”“9.父母包办”“10.经过互联网认识”。选择前4项的受访者被视为通过自由恋爱认识配偶(参照组)，其相应的相亲变量赋值为0；选择第5、6、7项的受访者被视为通过相亲认识配偶，其相亲变量赋值为1。由于“父母包办”、“网恋”不属于本文的讨论范围，且选择第8～10项的受访人相对较少，过小的样本量可能会造成估计偏差，我们删除了选择这3项的样本。

3.主要控制变量

外貌、工作满意度和信任度是主要的控制变量。CFPS访员对受访者的外貌进行了评价，外貌共分为7档，从1到7表示最丑到最美。CFPS将工作满意度分为5档，从1到5表示“非常不满意”到“非常满意”。信任度用“对陌生人的信任度”来表示，共有11档，“0”代表的信任度最低，“10”代表的信任度最高①限于篇幅，其他控制变量的说明省略，感兴趣的读者可以扫描本文二维码获取。。

4.基本估计方法

(1) 以婚姻满意度为因变量的样本称为样本一，以婚姻稳定性为因变量的样本称为样本二。对于样本一，由于婚姻满意度(主要衡量指标)及自家生活满意度均为有序离散变量，本文将采用有序Logit模型和有序Probit模型进行估计。

(2) 对于样本二，由于多数受访者在观察期内是在婚状态，我们无法观测到这些受访者的实际婚姻持续时间，则因变量存在数据删失问题，因而比较适合采用事件史分析法。具体而言，首先，本文以是否离婚作为婚姻稳定性的基本指标，建立离散时间的Logistic模型，如果受访者是在婚状态，则其婚姻持续时间的数据是删失的，因变量取值为0，如果受访者是离婚状态，则其婚姻持续时间的数据是完整的，因变量取值为1。其次，以婚姻持续时间为因变量的稳健性检验中，本文将运用事件史分析法中较为常用的Cox比例风险模型进行估计。Cox模型能解决数据删失问题，且不依赖于具体的风险分布假设，避免了异方差问题，回归结果更准确。需要注意的是，Cox模型的时间变量属于连续型，该模型成立的前提是比例风险假定；而Logistic模型的时间变量属于离散型，它可以克服Cox模型的缺陷(陈勇兵等，2012)，同时也能解决数据删失问题，因此，本文以离散时间Logistic模型的结果为准。

（三）估计结果分析

1.相亲与婚姻满意度

表1列(1)和列(2)报告了式(5)的有序Probit模型回归结果，列(4)和列(5)报告了式(5)的有序Logit模型回归结果。观测可知，不论在有序Probit模型还是有序Logit模型中，相亲的系数均显著为负，说明相对于恋爱式婚姻，相亲结婚的婚姻满意度更低。在控制夫妻年龄差距和婚龄变量后，相亲的系数仍然显著为负，说明回归结果稳健。列(7)和列(8)报告了以自家生活满意度为因变量的估计结果，两列相亲的系数均显著为负，这再次证明了估计结果的稳健性。列(3)和列(6)分别报告了式(6)的有序Probit模型、有序Logit模型的估计结果，在控制工作满意度、外貌等变量后，相亲的系数符号、显著性均未发生变化，说明考虑到个体的异质性影响后，相亲对婚姻满意度仍具有显著的负向影响。控制变量的回归结果和预期基本一致:(1)其他条件相同时，工作满意度越高，婚姻满意度也越高；长相越漂亮，婚姻满意度越高。(2)女性的回归系数显著为负，说明同等条件下，女性的婚姻满意度低于男性。(3)自评健康得分、和家人吃饭次数、社会地位与婚姻满意度成正相关关系，受教育年限与婚姻满意度成负相关关系。

表1 相亲对婚姻满意度的影响

2.相亲与婚姻稳定性

表2列(1)和列(2)报告了式(7)离散时间Logistic模型的估计结果，列(5)和列(6)报告了式(7)Cox比例风险模型的估计结果。观察可知，无论在离散时间Logistic模型还是Cox比例风险模型中，相亲的回归系数都显著为负，说明在控制健康自评、受教育年限、子女数等变量后，相亲式婚姻的离婚风险小于自由恋爱式婚姻。以列(2)为例，相亲的回归系数为-0.6826，说明相亲结婚夫妻的离婚风险仅为恋爱结婚的50.53%(e-0.6826)，换言之，相亲式婚姻的解体风险比恋爱式婚姻的解体风险低49.47%，相亲式婚姻更稳定。其可能的原因是，相亲的介绍人多为父母或亲戚，他们通常具备婚姻经验，因而较擅长判断相亲对象是否适合结婚。

表2列(3)和列(4)报告了式(8)离散时间Logistic模型的回归结果。在加入信任度和外貌等变量后，相亲的回归系数仍显著为负。就列(3)而言，控制外貌、信任度等变量后，相亲式婚姻的离婚风险仅为恋爱式婚姻的50.72%(e-0.6788)，这和列(2)的结果非常接近，说明无论是否控制个体差异的影响，相亲结婚的离婚风险均只有恋爱结婚的一半左右。列(7)和列(8)相应地报告了Cox比例风险模型的估计结果，在同时控制信任度和外貌变量后，相亲的回归系数仍为负，说明相亲式婚姻的解体风险显著低于恋爱式婚姻，这和Logistic模型的结论一致，回归结果较为稳健。据此认为，相亲确实降低了婚姻解体风险，进而提高了婚姻稳定性。

表2 相亲对婚姻稳定性的影响

四、样本选择偏差与内生性问题

（一）样本选择偏差

需要注意的是，式(5)和式(6)只能估计在婚样本的婚姻满意度，无法观测到离婚者或未婚者的婚姻满意度。同样地，受到因变量定义的限制，式(7)和式(8)仅能估计离婚者和在婚者的婚姻稳定性，未婚和丧偶的受访人则被排除在样本观测范围外。因此，上文的估计可能存在样本选择偏差(Heckman，1979)。由于婚姻满意度是有序多分类变量，是否离婚为二元变量，而传统的Heckman两阶段模型的第二阶段为OLS估计，因此，不宜采用传统的Heckman模型来纠正本文的样本选择性偏差。

1.Heckoprobit模型

针对样本一，我们建立Heckoprobit模型(De Luca和Perotti，2011)。首先，定义选择方程如下:

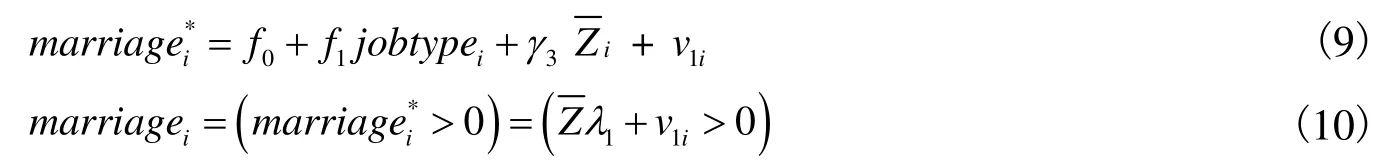
其中，r1、r2、r3、r4为实际切点，r0趋于无穷小，r5趋于无穷大。satfi为受访人对自身婚姻满意度的评分，从1到5表示婚姻满意程度依次提高。第二阶段的方程定义为:

其中，vh是实际观测到的值，服从二元正态分布，ε1i～N（0,1）。设ρ1是误差项ε1i和v1i的相关系数，根据上述设定，定义Xβ1+ε1i，则求得相应的极大似然函数如下:

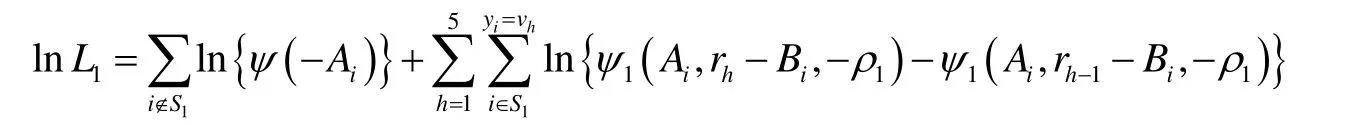
其中，S1是婚姻满意度可被观测到的所有样本集合，ψ1（⋅）是二元正态分布累积函数，ψ（⋅）是标准累积正态分布函数。

2.Heckprobit模型

针对样本二，本文建立Heckprobit模型(Van de Ven和Van Praag，1981)，具体设定如下:

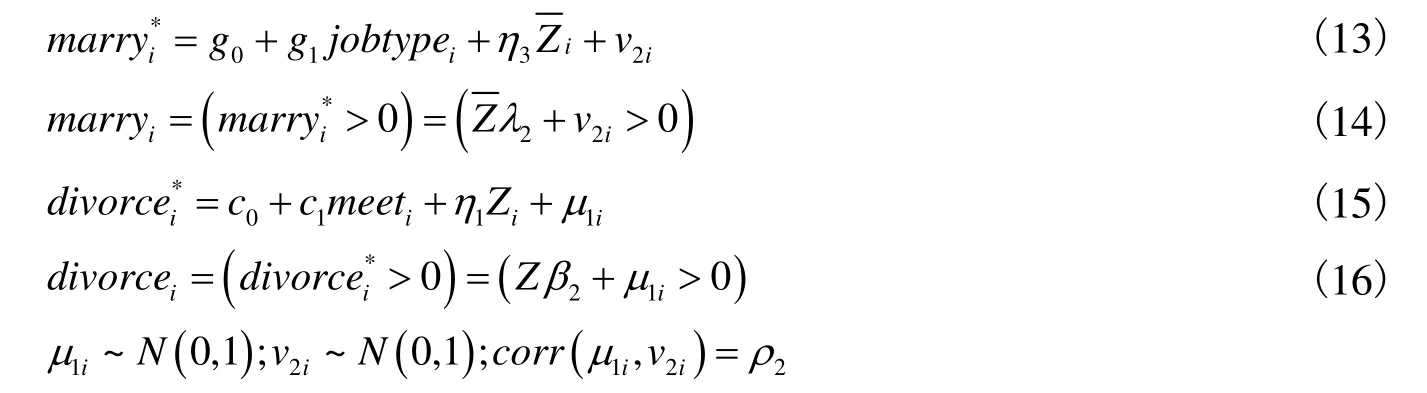
其中，是潜变量，表示受访人的婚姻经历，当时，虚拟变量marryi=1，表示受访人的婚姻状况为在婚或者离婚，婚姻稳定性相关信息可观测从而出现在样本二；否则，marryi=0，婚姻稳定性相关信息无法观测。本文认为，工作类型不仅影响婚姻状态，也是影响婚姻经历的重要变量，因此，我们仍将jobtypei作为选择方程的识别变量。是一组影响个体是否具有婚姻经历的控制变量。表示是否离婚的潜变量，当时，divorcei取值为1，表示离婚，否则，取值为0，表示在观测期内尚未离婚。其他变量的设定和式(7)相同。根据式(13)～式(16)，可求得相应的极大似然函数为:

其中，S2表示婚姻稳定性可被观测到的所有样本集合，φ1（⋅）是二元正态分布累积函数，φ是标准累积正态分布函数。

3.估计结果分析

表3前4列是Heckoprobit模型的回归结果，模型2在模型1的基础上，加入工作满意度、外貌变量，但相亲的系数值波动非常小，显著性也未发生改变，说明相亲的估计结果较为稳健。在模型1和模型2中，相亲的系数均显著为负，说明纠正了样本一的选择性偏差后，相亲对婚姻满意度仍具有负向影响。模型1的Wald检验P值远大于0.05，说明未通过5%的显著水平检验，模型2的Wald检验P值远大于0.10，据此认为，样本一基本上不存在样本选择性偏差。

表3后4列是Heckprobit模型的回归结果。观察可知，无论是否控制信任度、外貌变量，相亲的系数均在1%统计水平上显著为负，说明在纠正样本二的选择性偏差后，相亲仍显著降低了离婚风险。模型3和模型4的Wald检验P值均远大于0.10，因此，无法拒绝原假设“ H0：ρ2=0”，样本二不存在样本选择性偏差。

表3 Heckoprobit模型和Heckprobit模型的估计结果

（二）相亲的内生性问题

1.构建工具变量

需要注意的是，由于工作满意度、信任度和外貌变量均来自主观感受，且CFPS的外貌数据存在较大测量误差(郭继强等，2016)，式(6)加入工作满意度及外貌变量不一定能完全克服相亲的内生性问题。同理，式(8)通过加入信任度和外貌变量也不能真正解决相亲的内生性问题。因此，本文将构建2种工具变量。

首先，用“受访人的父母是否通过相亲认识对方”作为相亲的第1种工具变量。一般而言，父母是否相亲结婚将影响子女的相亲决策，而父母是否相亲结婚对子女的婚姻质量(包括婚姻满意度、婚姻稳定性)不具有显著影响。因此，可初步认为，父母是否相亲结婚是有效的工具变量。将个人编号、父亲编号、母亲编号和相亲变量进行配对，可获取父母是否相亲结婚的数据。

其次，考虑到年龄相仿的个体在相亲决策上表现出一定的趋同性，这里对年龄进行分组处理，按照年龄不超过25岁、26～30岁、31～35岁、36～40岁、41～45岁、46～50岁、51～55岁、56～60岁、61～70岁、70岁以上的划分标准分组。进一步地，按照受访人所在区县的城乡类型分组，计算区县城市层面、区县农村层面的各年龄组除受访人本人外的相亲变量均值。例如若受访人所属城乡类型为城市，年龄在26～30岁之间，则计算受访人所在区县的城市样本中除了本人之外的所有26～30岁群体的相亲变量均值。然而，采用区县-城乡层面除本人外的组内均值作为工具变量的方法虽可解决个体层面的变量遗漏问题，但并不是解决双向因果关系的有效方法(Gormley和Matsa，2016；Huang等，2016)，因此，本文选取父母相亲与区县-城乡层面本人所处年龄段的组内(本人除外)相亲均值的交互项作为第2种工具变量。

2.CMP估计法

针对样本一，前文采用有序Logit模型和有序Probit模型估计相亲对婚姻满意度的影响，但从技术可行角度来看，不能直接对排序模型使用工具变量法。针对样本二，前文采用离散时间的Logistic模型和Cox比例风险模型估计相亲对婚姻解体风险的影响。然而，对这两类模型均无法采用工具变量法，针对包含内生变量的二元选择模型，可采用IV-Probit模型进行估计。本文的内生变量相亲是二元变量，而IV-Probit只适用于内生变量为连续型变量的Probit模型。因此，为克服相亲的内生性问题，本文将采用前文的2种工具变量，借鉴条件混合过程(Conditional Mixed Process，简称CMP)估计法进行回归分析。参考Roodman(2011)，对于包含内生变量的有序Probit模型、有序Logit模型，将工具变量和CMP估计法相结合，可较好地解决模型的内生性问题。以样本一为例，运用CMP估计法需同时估计2个方程，第1个方程估计相亲对婚姻满意度的影响，即前文的式(5)，第2个方程以相亲为因变量，以工具变量为核心自变量，并加入第一个方程中除相亲外的所有其他自变量。

3.基于样本一的CMP估计结果分析

表4报告了以婚姻满意度为因变量的CMP估计结果。从相亲的估计系数来看，无论以父母相亲为工具变量，还是以交互项为工具变量，相亲的系数均显著为负，说明在控制相亲的内生性后，相亲对婚姻满意度仍具有负向影响。列(2)在列(1)的基础上加入工作类型变量，列(4)在列(3)的基础上加入工作类型变量，但相亲的系数符号均未发生变化，说明回归结果较为稳健。此外，考虑相亲的内生性后，控制变量的回归结果也和表1基本一致。

表4中，父母相亲对受访人相亲的影响系数显著为正，交互项工具变量与相亲正相关，且至少在1%统计水平上显著，说明父母相亲、父母相亲与区县-城乡-分年龄段相亲均值的交互项都符合工具变量的基本使用条件。为进一步检验工具变量的有效性，本文参考现有文献做法(Chyi和Mao，2012)，借用线性模型的弱工具变量检验方法，对表4的回归1～回归4进行检验，结果如表5所示。根据表5，各列F统计量均大于10，且至少在1%统计水平上显著。同时，名义显著性水平为5%的Wald检验结果显示，最小特征值统计量远大于10%的临界值。据此，我们有充足理由认为不存在弱工具变量。

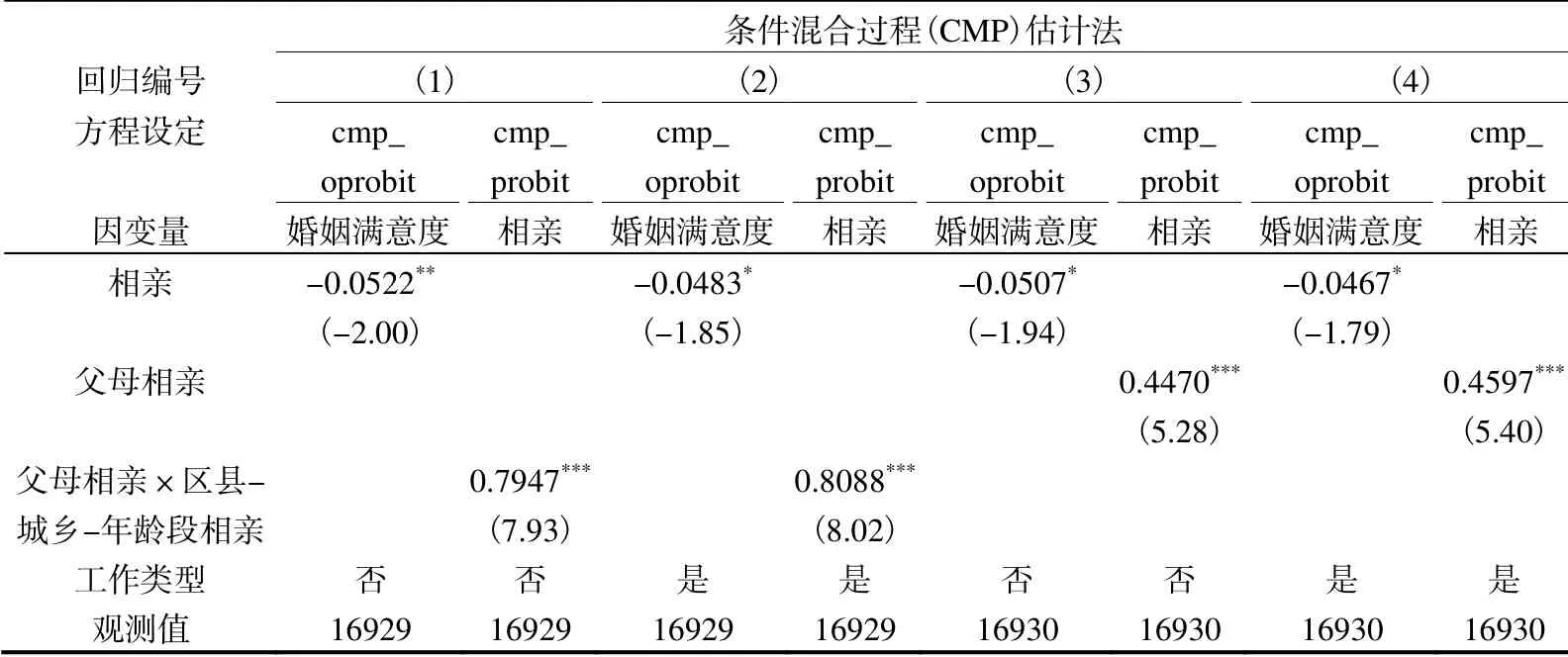
表4 相亲对婚姻满意度的影响——基于样本一的CMP估计结果

表5 弱工具变量检验

根据表4，我们只能判断相亲对婚姻满意度的影响方向，表6报告了表4回归1～回归4的相应边际效应。从表6可知，非常满意的系数显著为负，说明相亲式婚姻的满意程度为非常满意的可能性显著低于自由恋爱式婚姻的满意度，即恋爱结婚的夫妻更有可能获得最高水平的婚姻满意度。

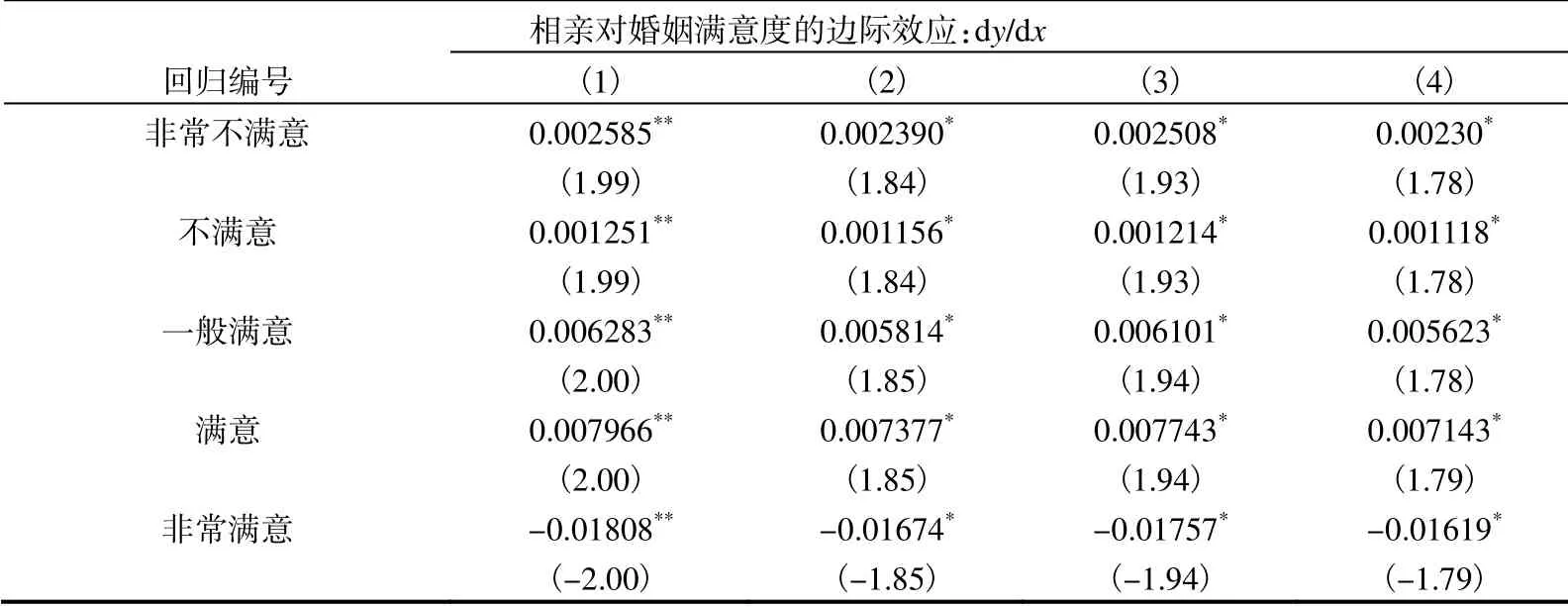
表6 基于CMP估计结果的边际效应

4.基于样本二的CMP估计结果分析

表7报告了以是否离婚为因变量的CMP估计结果。回归1和回归2选取交互项为工具变量，回归3和回归4选取父母相亲为工具变量，且回归2和回归4加入了工作类型变量。在回归1～回归4中，相亲的系数均显著为负，说明在克服相亲的内生性问题后，相亲结婚的离婚风险仍然显著低于恋爱结婚，相亲提高了婚姻稳定性。控制变量的显著性、正负符号均和表2一致，这从侧面佐证了回归结果的稳健性。

同样，这里需要检验工具变量的有效性。表7中，两种工具变量均和相亲正相关，说明满足工具变量的必备条件。同时，我们基于表7回归1～回归4，进行弱工具变量检验，操作和表5类似，结果发现，F统计量均在1%水平上显著且远大于10，最小特征值统计量均超过10%的临界值，故拒绝“弱工具变量”的原假设①因篇幅有限，未在文中列出，感兴趣的读者可以扫描本文二维码获取。。

表7 相亲对婚姻稳定性的影响——基于样本二的CMP估计结果

（三）夫妻相对收入与婚姻质量

既有研究表明，夫妻收入比一定程度上反映了夫妻双方的家庭相对地位，收入是影响婚姻的重要因素(Autor等，2017)。为了验证夫妻相对收入对婚姻质量的影响，我们对受访人配偶的工资数据进行配对，删除缺失数据，用妻子年收入与丈夫年收入的比值来衡量夫妻相对收入②这里感谢匿名评审专家的建设性意见。。

1.相对收入与婚姻满意度

表8报告了以婚姻满意度为因变量的估计结果。表8回归1和回归2分别是有序Logit、有序Probit模型的估计结果，夫妻相对收入比的系数为负，但不显著。表8回归3和回归4是CMP估计结果，在控制相亲的内生性后，夫妻相对收入比仍不显著。据此认为，夫妻相对收入地位不是影响婚姻满意度的显著性因素。此外，回归1～回归4中，相亲的系数均显著为负，说明在控制夫妻相对收入地位后，相亲结婚的婚姻满意度均低于恋爱结婚，这和前文的结论一致。

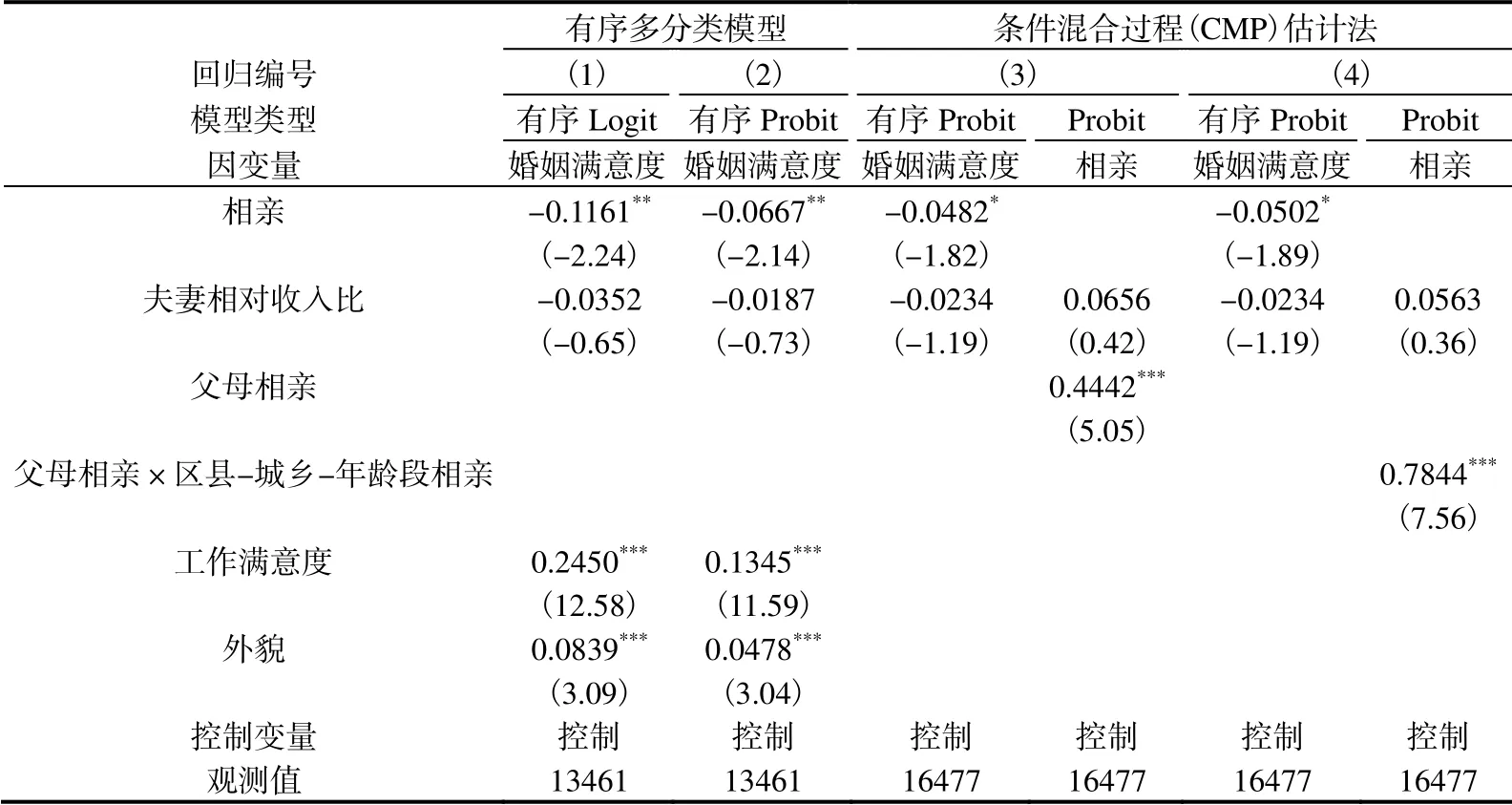
表8 夫妻相对收入影响婚姻满意度吗

2.相对收入与婚姻稳定性

本文以是否离婚为因变量进行估计。结果发现，妻子的收入越高，婚姻解体的风险越大，夫妻在经济上的势均力敌有利于维持婚姻稳定。然而，控制了相亲的内生性问题后发现，夫妻相对收入比并非是影响婚姻稳定性的决定性因素①因篇幅有限，未在文中列出，感兴趣的读者可以扫描本文二维码获取。。

五、作用机制分析

相亲与自由恋爱的本质区别在于:相亲对象由介绍人选定，介绍人无法判断相亲双方是否产生感情及结婚后的恩爱程度，因而情感信息不对称，相亲对象可能不是最佳匹配对象。夫妻匹配度是否为相亲影响婚姻质量的主要因素？这是接下来验证的内容①因篇幅有限，未在文中列出，感兴趣的读者可以扫描本文二维码获取。。

1.中介变量的界定

本文将匹配度分为物质匹配度和精神匹配度。(1)参考周广肃和孙浦阳(2017)，本文将“对物质的看重程度”定义为自评经济地位与实际经济地位的比值。两者比值越小，表明对物质的看重程度越高。物质匹配度用受访人与其配偶对物质看重程度的差距来表示。CFPS直接询问了受访人在本地的自评经济地位，回答分值为1～5的任意整数，分值越大，则自评经济地位越高。同时，本文将实际经济地位分为5个档，用受访人的个人年收入在所属省份的等级来表示。(2)本文拟从“家庭观”和“婚姻观”两方面来衡量精神匹配度。CFPS就“家庭观”设计了6个问题:“子女应善待父母”“子女应达成父母心愿”“儿子婚后和父母住在一起”“应至少生一个儿子”“应当做光宗耀祖的事情”“应经常回家探望父母”，CFPS还就“婚姻观”设计了4个问题，我们将受访人与其配偶对上述10个问题的答案进行匹配，每个问题的匹配程度用两者差值的绝对值表示，则受访人与其配偶在每个问题上的匹配程度为取值为0～4的整数，取值越大，表示两者在该问题的匹配程度越低，若两者回答完全一致，则取值为0，表示完全匹配。这样，我们共获取10个匹配程度变量。然而，这10个变量之间可能存在显著的相关关系，本文将运用主成分法进行降维处理。值得一提的是，传统的主成分分析法(PCA)只能用于线性变量，而SPSS软件的CATPCA方法则适用于有序分类变量的主成分分析(Meulman和Heiser，2009)，本文将借助CATPCA方法，将上述10个匹配程度变量合成一个综合指标，并将该指标定义为精神匹配度。

2.中介效应模型

需要注意的是，CFPS没有直接提供受访人配偶的自评经济地位、家庭观、婚姻观等数据，我们基于个人代码和其配偶代码进行数据配对，获取配偶相关数据。为检验相亲是否通过影响匹配度进而影响婚姻质量，我们以物质匹配度、精神匹配度作为中介变量，建立中介效应模型。Sobel(1982)提出的中介效应系数乘积项检验法仅适用于线性中介效应模型，而本文的中介效应模型为非线性模型。Breen等(2013)提出的KHB方法，既能用于非线性概率模型的中介效应分析，也适用于多维中介变量的情形，因此，本文采用KHB方法来检验匹配度是否为相亲影响婚姻质量的渠道。

图1表示相亲对婚姻质量的作用机制，根据图1，相亲经由匹配度路径进而对婚姻质量产生的影响称为中介效应，相亲不经由任何路径而直接对婚姻质量产生的影响称为直接效应。中介效应和直接效应的加总则是相亲对婚姻质量的总效应。

图1 机制分析

3.基于KHB方法的中介效应分析

这里仍然从婚姻满意度和婚姻稳定性两方面来衡量婚姻质量，基于图1进行中介效应检验。表9报告KHB方法的检验结果，前4列以婚姻满意度为因变量，后4列以是否离婚为因变量。列(1)、列(2)、列(5)、列(6)以精神匹配度为中介变量，仅列(1)和列(2)的中介效应系数显著为负，说明夫妻之间的精神匹配度是相亲影响婚姻满意度的显著性路径，相亲通过影响夫妻在家庭观和婚姻观方面的观点匹配程度进而对婚姻满意度产生显著的负向影响。然而，精神匹配度不是相亲影响婚姻稳定性的显著性路径。列(3)、列(4)、列(7)、列(8)以物质匹配度为中介变量，这4列的中介效应均不显著，说明物质匹配度未发挥显著的中介作用。

表9 基于KHB方法的中介效应检验

六、结 论

相亲式婚姻是否真的靠谱？对该问题的研究对广大单身人士及催婚父母具有重要意义。本文遵循理论-实证的研究路线，分析相亲对婚姻满意度、婚姻稳定性的影响。首先，本文将2种婚姻匹配方法纳入理论模型(相亲和自由恋爱)，结果表明，自由恋爱式婚姻比相亲式婚姻的效用更高，相亲式婚姻比自由恋爱式婚姻更稳定。

其次，基于理论假说，我们运用CFPS2014年的数据，建立有序Logit模型、有序Probit模型来分析相亲对婚姻满意度的影响，建立离散时间Logistic模型、Cox比例风险模型来分析相亲对婚姻稳定性的影响。实证结果和理论假说一致，说明相亲降低了婚姻满意度，但也导致了更稳定的婚姻。实证结果还表明，控制其他相关变量后，长相越漂亮，婚姻满意度更高，然而，是否漂亮对婚姻稳定性无显著性影响。这和现实相符，漂亮的人不一定擅长处理婚姻生活中出现的问题，长得漂亮不意味着婚姻稳定。考虑到样本选择性偏差，本文分别以婚姻满意度、是否离婚为因变量，分别建立Heckoprobit模型和Heckprobit模型，结果发现，在考虑样本的选择性偏差后，相亲对婚姻满意度仍具有负向影响，相亲有利于降低离婚风险。同时，考虑到相亲的内生性问题，我们构建2种工具变量，即父母是否相亲结婚、父母是否相亲与区县-城乡-同年龄段相亲的交互项，运用CMP估计法进行回归分析，实证结果再次验证了理论假说。此外，控制妻子丈夫收入比后，上述结论仍然成立。

本文的结论可用Becker(1974)的婚姻论和Becker(1991)的家庭论来解释:婚前的信息不完备致使相亲结婚对象往往不是最佳结婚人选，因而同等条件下相亲式婚姻的满意度较低；尽管自由恋爱式夫妻在婚前的信息相对完备，但随着时间的推移和双方的改变，边际效用递减，婚姻解体的风险增加①这里感谢匿名评审专家的建设性意见。。通过相亲来认识结婚对象的群体，其本身可能比自由恋爱群体更传统，中国自古以来流传的“宁拆十座庙，不破一桩婚”、“好人不离婚，离婚不正经”等不能离婚的伦理文化对相亲群体的影响较大，离婚带来的社会舆论压力也可能降低了相亲群体的离婚意愿。

最后，本文构建夫妻匹配度指标，以物质匹配度、精神匹配度为中介变量，建立中介效应模型，分析相亲对婚姻质量的影响渠道。KHB方法的估计结果表明，相亲通过影响夫妻之间的精神匹配程度进而降低了婚姻满意度，精神匹配度是相亲影响婚姻满意度的重要渠道，而物质匹配度不是相亲影响婚姻质量的显著性渠道。

本文的研究结论具有较强的现实意义，在同等条件下，相亲降低了婚姻满意度，这为单身人士抵触相亲的行为提供了一个合理化解释，同时，相亲提高了婚姻稳定性，这为广大父母推动的相亲潮提供了一个正面的评价。本文的结论还从侧面说明，幸福的婚姻不一定持久，这印证了网络上的一句话“有多少爱情败给了时间”。