超导磁悬浮储能及姿控飞轮的永磁结构仿真

程 诚，林庆国，张志远

(1.上海空间推进研究所，上海 201112；2.上海空间发动机工程技术研究中心，上海 201112)

0 引言

近年来，微小卫星的发展十分迅速，其功能不断增加，实用性也不断提高，很有可能改变原先以大卫星为主导的卫星体系结构[1-2]。为进一步提高其性能，空间有限的微小卫星需要采用具有复合功能的组件。储能及姿控飞轮既有寿命长、储能密度高以及能量转换效率高等优点，又有控制精度高和适用范围广的特点，从而能很好地适用于微小卫星[3]。

从2002年开始，美国NASA着力研制一种满足于长期任务需求的储能及姿控飞轮，并于2004年推出了采用机械轴承和永磁轴承的G2飞轮，其储存能量为525 W·h，重量约99 kg，可在90 min内实现90%的深度放电[4]。国内的中国科学院长春光机所[5-7]、哈尔滨工业大学[8]和东华大学[9]等也对该型飞轮的结构设计、控制系统和试验测试做了大量的研究工作。其中，程千兵等[7]着重对超导磁悬浮储能及姿控飞轮进行了系统设计和试验测试工作，发现超导飞轮在空气中的最高转速可达15 000 rpm，摩擦损耗却远远小于机械轴承。Eunjeong Lee[10]提出了另外一种应用于微小卫星的超导飞轮，其储能密度达到了45 W·h/kg，能耗只有10 W左右，适用于近地轨道的微小卫星。

虽然超导飞轮有诸多的优点，但是超导储能及姿控飞轮的结构依然存在诸多可以优化的地方。基于Comsol Multiphysics仿真软件，本文从磁场的角度入手，以最大悬浮力为优化目标，同时兼顾敏感元件区域的磁场分布，进行了耦合超导结构和永磁结构的磁场仿真计算。通过对比3种转子的永磁结构，选择Halbach构型作为超导飞轮的永磁结构，并在给定设计尺寸的情况下，通过调整永磁结构尺寸获得了最优的永磁构型。

1 计算模型

为了研究超导磁悬浮储能及姿控飞轮的性能特点，提出了如图1所示的地面试验装置。该装置整体位于真空舱中，主要结构为一对反转的超导飞轮组件，其中的每个组件均包括一个转子、一个定子以及两台小型斯特林制冷机。从空间应用的角度来说，转子质量一定的前提下，应合理设计其永磁结构使得永磁转子与超导定子的悬浮力最大。本文在给定基本尺寸情况下，以最大悬浮力为目标，同时兼顾转子背面—星上敏感元件区域的磁场强度大小，进行永磁结构的优化设计。由于转子的永磁结构和定子的超导阵列环均为相应块材拼接的圆环，忽略缝隙的影响，计算采用2D轴对称模型，计算模型和网格划分如图2所示，永磁结构和超导结构的设计尺寸如表1所示。

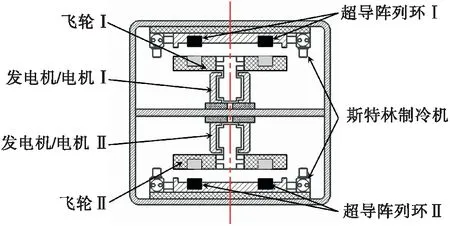
图1 超导磁悬浮储能及姿控飞轮地面试验装置示意图Fig.1 Schematic of ground test device for the HTS maglev energy storage and attitude control flywheel

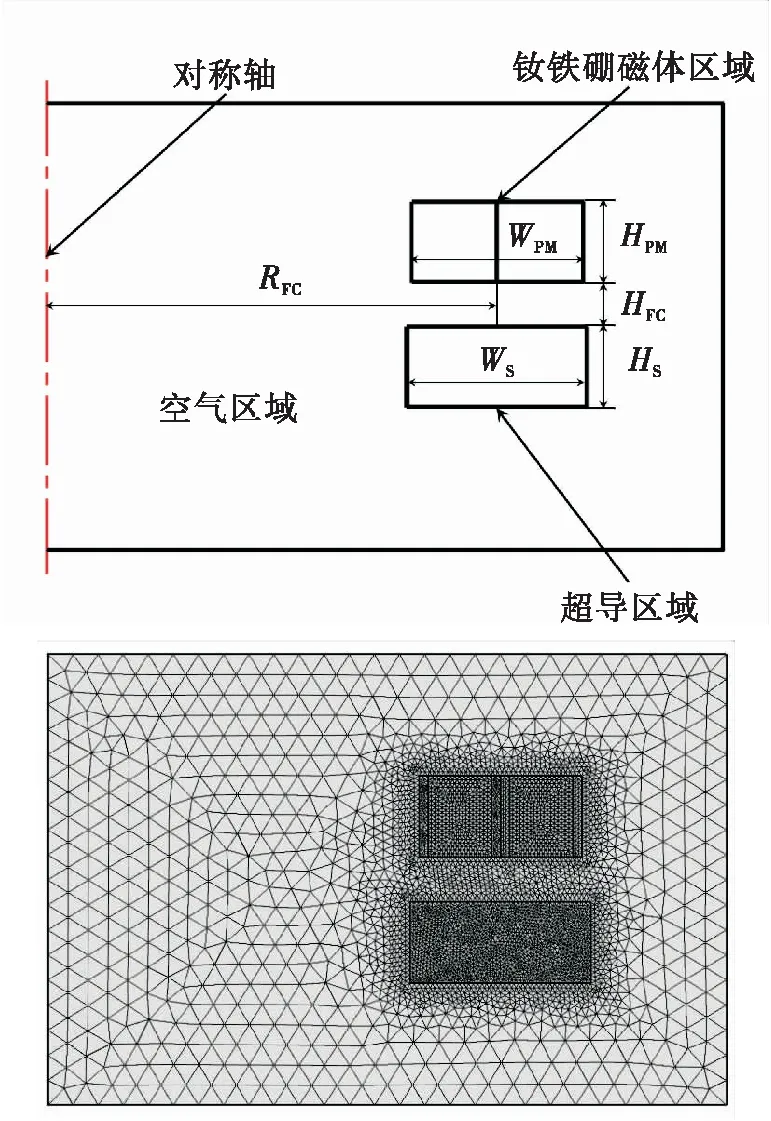
图2 计算模型和网格划分Fig.2 Calculation model and mesh

结构参数尺寸/mmRFC100WFC36HFC18WS40HS18

2 计算方法

仿真计算以磁场强度H作为独立变量，即为H方法，整个求解域内满足Maxwell方程：

(1)

式中:E为电场强度;μ0为真空磁导率；μr为相对磁导率；J为电流密度。仿真计算重点在于对超导材料本构关系的处理。本文所采用的超导体为YBCO块材，其磁导率为线性的，但其电导率却是高度非线性的。YBCO区域内E-J关系用指数关系描述：

(2)

式中:ES为超导体内的电场；E0和n为由试验确定的常量，分别取0.083 616 8 V/m和21；JC(B)为受外磁场影响的YBCO超导体临界电流密度；JC0和B0为由试验确定的常量，分别取17 MA和0.7 T[11]。永磁结构区域则通过施加面电流来模拟N45钕铁硼材料。永磁结构所受悬浮力按下式计算：

Fz=JC(B)×B

(3)

图3给出了单块YBCO超导体/钕铁硼永磁体的悬浮力试验数据和仿真计算结果的对比。可以看出，仿真结果与试验测量数据基本吻合，但是计算得到的悬浮力最大值相比实测结果偏小约16%。然而，从保守设计角度来说，本文采用的仿真计算方法是可行的。

图3 YBCO块材(Φ30 mm×H20 mm)与钕铁硼永磁体(Φ30×H30 mm)悬浮力试验与仿真结果Fig.3 Experimental and simulational levitation forces of the YBCO (Φ30 mm×H20 mm) and NdFeB permanent magnet (Φ30 mm×H30 mm)

3 计算结果与分析

3.1 永磁构型选择

稳定超导磁悬浮的实现要求永磁结构应满足的条件为：所提供的外磁场相对于超导块材的轴向是对称的。这样可以最大程度地保证侧向力的平衡。满足这个条件的永磁构型主要有3种，如图4所示。

图4 3种相对于超导体轴向对称的永磁结构示意图Fig.4 Three permanent magnetic structures relative to HTS axial symmetry

1)构型Ⅰ(轴向顺排型)：磁结构所采用的一对永磁体均为轴向磁化，指向超导体的端面，与其轴向平行。

2)构型Ⅱ(径向聚磁型)：磁结构所采用的一对永磁体磁化方向相对，沿径向方向。

3)构型Ⅲ (Halbach型)：磁结构所采用的一对径向磁化的永磁体之间有一个磁化方向指向超导体端面的永磁体。

图5分别给出了上述3种永磁构型耦合超导阵列环的磁场计算云图。在构型Ⅰ中，超导阵列环仅有边缘上部少量的区域有磁场穿透，其余区域均因Meissner效应而没有磁场穿透。此外，超导阵列环与永磁结构之间也存在大片零磁场区域。由于聚磁结构的磁场较强，在构型Ⅱ和构型Ⅲ中，超导阵列环的磁场穿透的区域增加并向中心靠拢，其与永磁结构之间零磁场区域也进一步缩小。从图5可看出，构型Ⅱ与构型Ⅲ的区别在于：构型Ⅱ上部磁场强度略高于下部，而构型Ⅲ磁场主要集中在下部。构型Ⅲ中超导阵列环的磁场和电流密度分布如图6所示。由图6可见，电流分布区域与磁场分布区域较为一致，这也是超导体Meissner效应的重要体现。

图5 3种永磁构型耦合超导阵列环的磁场计算云图Fig.5 Calculated magnetic fields for the three permanent magnetic structures coupled with HTS array loop

图6 构型Ⅲ Halbach永磁构型中超导阵列环内部的 磁场密度和电流密度分布图Fig.6 Magnetic density distribution and electric current density distribution of the HTS array loop for Type-III Halbach permanent magnetic configuration

采用时间非定常计算，通过调整面电流大小使永磁结构的磁场在1 s内从零增加到设计值，并根据式(3)计算悬浮力，结果如图7(a)所示。由图可见，构型Ⅲ的悬浮力始终最大，构型Ⅱ次之，而构型Ⅰ最小。由于构型Ⅰ没有采用聚磁结构，其磁场是最小的。虽然式(2)给出YBCO材料的电流密度随外磁场的增强而减小，但是构型Ⅰ中超导阵列环的电流区域过小，导致其产生的悬浮力也是最小的。相应地虽然构型Ⅲ的最大电流密度1.30×108A/m2要小于构型Ⅱ的1.32×108A/m2和构型Ⅰ的1.39×108A/m2，但是其电流区域最大，故所产生的悬浮力是最大的。

图7(b)给出了计算结束时刻(1.00 s)时，永磁结构正上方20 mm区域(r: 80～120 mm)的磁场分布。构型Ⅰ磁场是最高的，构型Ⅱ次之，构型Ⅲ最小。虽然构型Ⅰ的磁场较弱，但其为一发散场，磁场强度随距离的增加衰减得较慢。构型Ⅱ和构型Ⅲ均为聚磁结构，随着距离的增加，二者磁力线方向较为迅速地转向水平，流向另外一极。二者不同之处在于：由于Meissner效应，构型Ⅱ永磁结构的磁力线更多地向上部汇集，其上部磁场较高；由于Halbach构型的采用，构型Ⅲ永磁结构的磁力线更多从下部流向另外一极，其上部磁场较小。由于转子的背面为卫星的敏感元件区域，需防止过大的磁场干扰仪器设备。综合分析，构型Ⅲ永磁构型在悬浮力和削弱背面磁场方面均有一定的优势，所以转子的永磁结构建议采用Halbach构型。

图7 3种永磁构型的悬浮力计算结果和永磁结构上方20mm处的磁场分布Fig.7 Calculated levitation forces and magnetic fields (20mm above permanent magnetic structure) of the three configurations

3.2 Halbach构型永磁结构优化

为获得更大的悬浮力以增强承载能力和飞轮的稳定性，本文对构型Ⅲ Halbach构型的永磁结构进行了优化设计。优化的结构参数包括：中心磁体宽度WCPM和中心磁体高度HCPM，如图8(a)和图9(a)中的内嵌图所示。优化的步骤为：保持永磁结构总体尺寸不变，改变WCPM进行计算，以悬浮力最大为目标，参考永磁结构上方磁场计算结果，得到最优的中心磁体宽度；将WCPM固定在所得最优宽度上，改变HCPM进行计算，兼顾磁场计算结果，得到最优的中心磁体高度。

图8给出了永磁结构悬浮力及其上方20 mm处的磁场峰值与中心磁体宽度的关系。

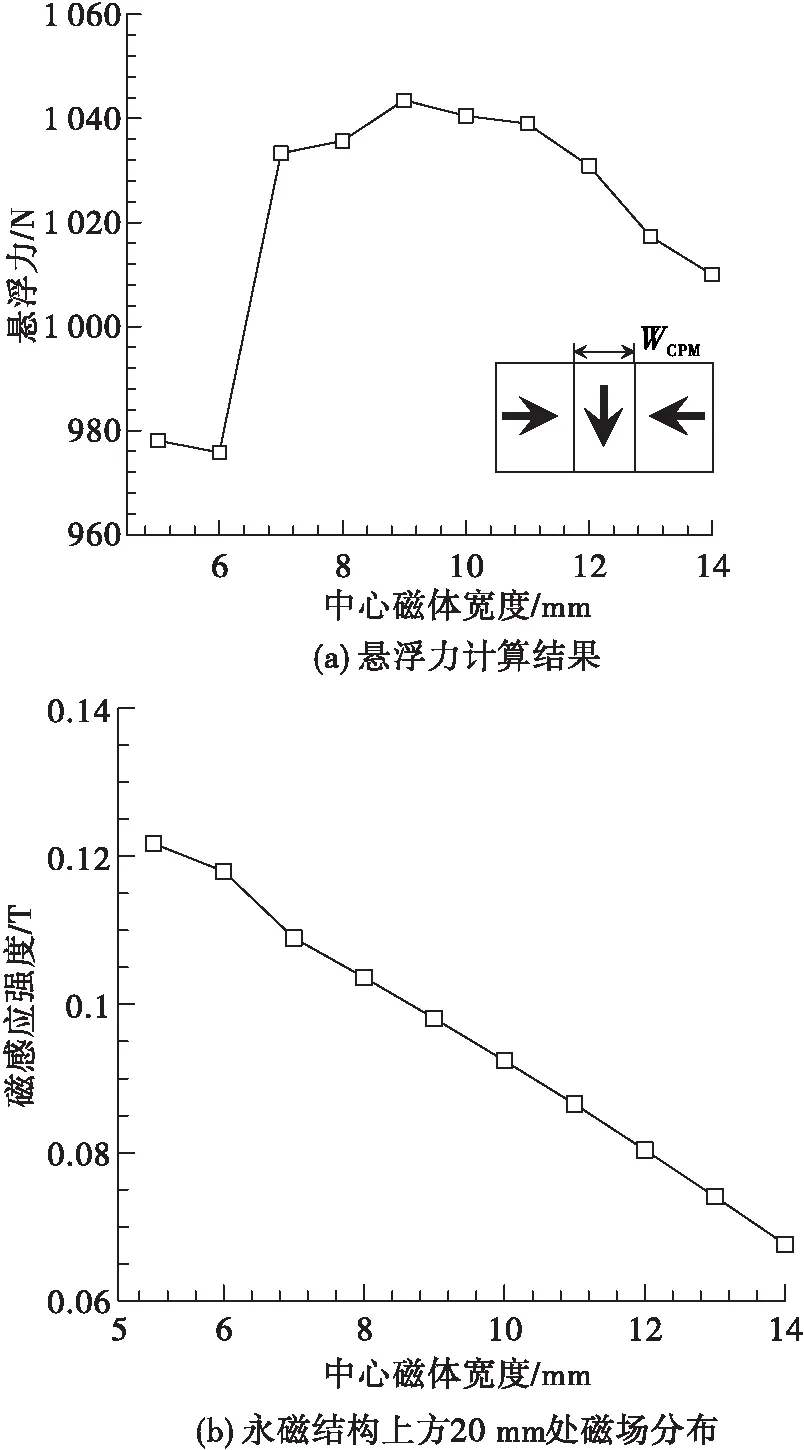
图8 永磁结构悬浮力及其上方20mm处的磁场峰值与中心磁体宽度的关系Fig.8 Relationship between the levitation force and magnetic peak (20 mm above permanent magnetic structure) with the center’s width

在WCPM为5～14 mm的优化范围内，悬浮力在9 mm处存在一个最优点，达到了1 043.5 N，而磁场强度则随着WCPM的增加而减小，从5 mm时的0.12 T降低至14 mm时的0.67 T。虽然WCPM取9 mm时悬浮力计算值最大，但本文决定采用10 mm作为最优的中心磁体宽度。这是因为：当WCPM在9～8 mm范围时，悬浮力由1 043.5 N降低至1 035.7 N；当WCPM在9～11 mm范围时，悬浮力的范围则是从1 043.5 N变化到1 039.0 N。可见，把最优宽度定为10 mm可以避开实际操作中尺寸微小差异引起的悬浮力较大变化。

图9(a)和图9(b)则给出了永磁结构悬浮力及其上方20 mm处的磁场峰值与中心磁体高度的关系。当HCPM为16 mm时，悬浮力达到最大值1 083.9 N；永磁结构上方磁场随着磁体高度的增加而增强。采用不等高的中心磁体可使永磁下部的磁场进一步汇聚，进而产生更强的悬浮力，但由于破坏了上部磁路，使上方磁场更呈现一个发散场的特性。通过优化计算，在给定永磁结构区域尺寸和超导区域尺寸下，得到了Halbach构型永磁结构的最优WCPM=10 mm和HCPM=16 mm。

图9 永磁结构悬浮力及其上方20 mm处的磁场峰值与中心磁体高度的关系Fig.9 Relationship between the levitation force and magnetic peak (20 mm above permanent magnetic structure) with the center’s height

4 结论

本文基于Comsol Multiphysics仿真软件，采用2D轴对称简化计算模型，应用H方法对超导磁悬浮储能及姿控飞轮的永磁结构转子磁场分布和悬浮力进行仿真计算与分析。算例验证结果和试验测量结果基本吻合，误差在工程允许范围之内，表明所采用的仿真计算方法合理可行。通过对比分析3种符合要求的永磁构型，发现Halbach构型的永磁结构在增大悬浮力和削弱转子背面敏感元件区域磁场方面均有较明显的优势。在保持永磁区域尺寸不变的情况下，通过调整中心磁体的宽度和高度，以悬浮力最大为优化目标，同时兼顾永磁结构上方区域的磁场强度，获得了最优的Halbach永磁构型。