Solving the Nonlinear Variable Order Fractional Differential Equations by Using Euler Wavelets

Yanxin Wang,Li Zhu and Zhi Wang

Abstract: An Euler wavelets method is proposed to solve a class of nonlinear variable order fractional differential equations in this paper.The properties of Euler wavelets and their operational matrix together with a family of piecewise functions are first presented.Then they are utilized to reduce the problem to the solution of a nonlinear system of algebraic equations.And the convergence of the Euler wavelets basis is given.The method is computationally attractive and some numerical examples are provided to illustrate its high accuracy.

Keywords:Euler wavelets,variable order fractional differential equations,caputo fractional derivatives,operational matrix,convergence analysis.

1 Introduction

Many phenomena in fluid mechanics,chemistry,physics,finance and other sciences can be described successfully by models using mathematical tools from fractional calculus,i.e.the theory of derivatives and integrals of fractional order [Miller and Ross (1993)].Due to the fractional order exponents in differential operators,analytical solutions of fractional equations are usually difficult to obtain.Consequently,different methods have been developed to give numerical solutions for fractional equations,including fractional differential transform method [Wei and Chen (2014)],Adomian decomposition method [Song and Wang(2013)],Chebyshev pseudo-spectral method[Khader and Sweilam(2013)],Homotopy perturbation method[Abdulaziz,Hashim and Momani(2008)],Homotopy analysis method[Dehghan,Manafian and Saadatmandi(2010)],and wavelet method[Li and Zhao(2010);Wang and Fan(2012);Wang and Zhu(2016)].

Recently,the concepts of fractional derivatives of variable order have been introduced and some research works of the relative practical applications have arisen[Sun,Chen and Chen(2009);Samko (2013)].Several numerical approximation methods are proposed to solve the variable order fractional differential equation [Chen,Liu,Li et al.(2014);Chen,Liu,Turner et al.(2013);Lin,Liu,Anh et al.(2009);Chen,Wei,Liu et al.(2015);Zhao,Sun and Karniadakis (2015);Zayernouri and Karniadakis (2015);Li and Wu (2017);Jia,Xu and Lin(2017);Doha,Abdelkawy,Amin et al.(2018)].

Recently,a Euler wavelet numerical method has been presented to solve the nonlinear Volterra integro-differential equations [Wang and Zhu (2017)].The Euler wavelets are constructed by Euler polynomials.It is well known that Euler polynomials have many advantages over Legendre polynomials in approximating arbitrary functions.Fristly,the Euler polynomials have less terms than Legendre polynomials.Hence,for approximating an arbitrary function,we use less CPU time by applying Euler polynomials as compared to Legendre polynomials.Secondly,the computational errors are less by using Euler polynomials in function approximation.Therefore,we have reason to believe that Euler wavelets inherit these advantages of Euler polynomials.So the main purpose in this paper is to introduce the Euler wavelets operational matrix method to solve the nonlinear variable order fractional differential equation.The Euler wavelets method is based on reducing the equation to a system of algebraic equations by expanding the solution as Euler wavelets with unknown coefficients.The convergence analysis of the Euler wavelets basis is given.Also the characteristic of the operational matrix method is to transform the differential equations into the algebraic one.It not only simplifies the problem,but also speeds up the computation.

The outline of this paper is as follows:In Section 2,some necessary mathematical preliminaries and notations of variable order fractional derivatives are given.Section 3 is devoted to the basic formulation of wavelets and the Euler wavelets.In Section 4,we derive the Euler wavelets operational matrices.Section 5 is devoted to the numerical method for solving the variable order fractional differential equations,and in Section 6 we report our numerical findings and demonstrate the accuracy of the proposed numerical scheme by considering two numerical examples.Finally,conclusions are drawn in last Section.

2 Basic definitions and properties of the variable order fractional integrals and derivatives

There are several definitions for variable order fractional derivatives,such as the one in Riemann-Liouville’s sense and the one in Caputo’s sense[Samko(2013)].

Definition 1.Riemann-Liouville fractional integral of the first kind with orderα(t) is defined as

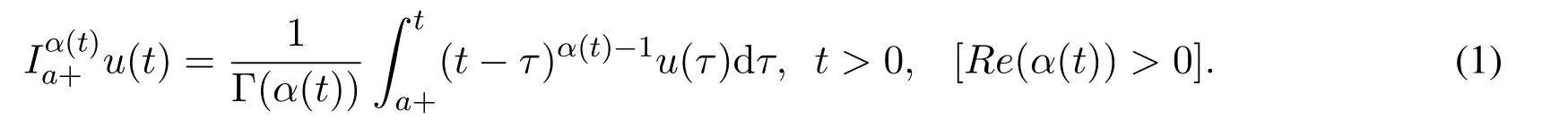
Definition 2.Riemann-Liouville fractional derivate of the first kind with orderα(t) is defined as

Definition 3.The Caputo definition of fractional derivate with orderα(t)

where 0＜α(t)≤1.If we assume the starting time in a perfect situation,we can get the definition as follows:

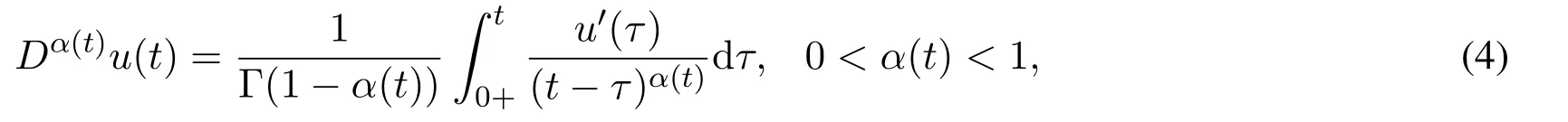
with the definition above,we can get the following formula(0＜α(t)≤1)

3 Euler wavelets and function approximation

3.1 Euler wavelets

Euler waveletsψnm(t) =ψ(k,n,m,t) involve four arguments,n= 1,...,2k-1,kis assumed any positive integer,mis the degree of the Euler polynomials andtis the normalized time.They are defined on the interval[0,1)as[Wang and Zhu(2017)]

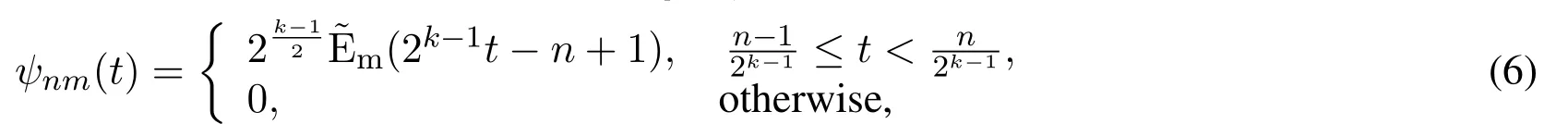
with

wherem= 0,1,...,M -1 andn= 1,...,2k-1.The coefficientis for normality,the dilation parameter isa= 2-(k-1)and the translation parameterb=(n-1)2-(k-1).Here,Em(t)are the well-known Euler polynomials of ordermwhich can be defined by means of the following generating functions[He(2015)]

In particular,the rational numbersEm= 2mEm(1/2)are called the classical Euler numbers.Also,the Euler polynomials of the first kind form= 0,··· ,Ncan be constructed from the following relation

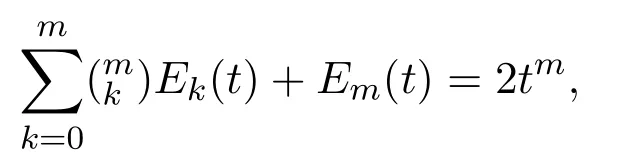
where(mk)is a binomial coefficient.Explicitly,the first basic polynomials are expressed by

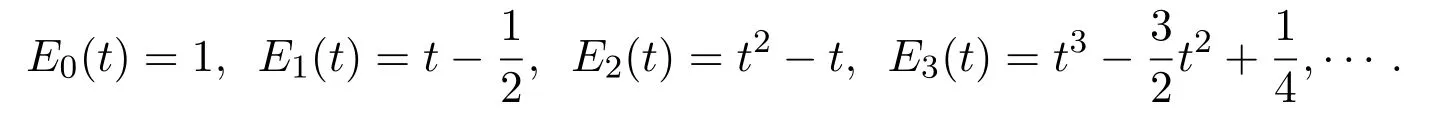
These polynomials satisfy the following formula

Euler polynomials form a complete basis over the interval[0,1].Furthermore,whent=0,we have

3.2 Function approximation

A functionf(t),square integrable in[0,1],may be expressed in terms of the Euler wavelets as

and we can approximate the functionf(t)by the truncated series

where the coefficient vectorCand Euler function vector Ψ(t)are given by

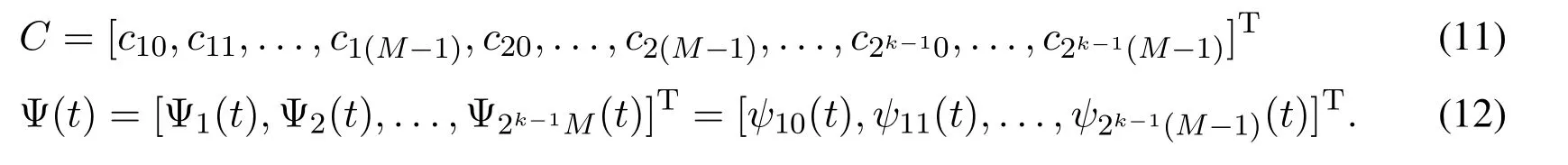
To evaluateC,we letUsing Eq.(10)we obtain

whereandi=1,2,··· ,2k-1,j=0,1,··· ,M -1.

Therefore,

with

and

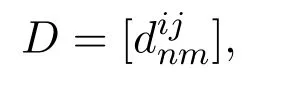
whereDis a matrix of order 2k-1M ×2k-1Mand is given by

The matrixDin Eq.(13) can be calculated by using Eq.(9) in each intervaln=1,2,··· ,2k-1.

Hence,CTin Eq.(10)is given by

We investigate the convergence of the Euler wavelets expansion in the following Theorem.

Theorem 4.Suppose that the functionf:[0,1]→R ism+1 times continuously differentiable andf ∈Cm+1[0,1].Then ˜f(t) =CTΨ(t)approximatef(t)with mean error bounded as follows

Proof:The proof is similar to that of the Theorem 1 in Wang et al.[Wang and Zhu(2017)],so it is omitted here.

4 Operational matrix of Euler wavelets

4.1 A new family of functions

Since Euler wavelets functions are formulated based on polynomials,a family of functions defined on[0,1]is constructed as follows

forn=1,2,...,2k-1,m=0,1,...,M -1.Unlike Euler wavelets functions,this family of functions is not normalized.The connection between these functions and Euler wavelets can be demonstrated as follows:

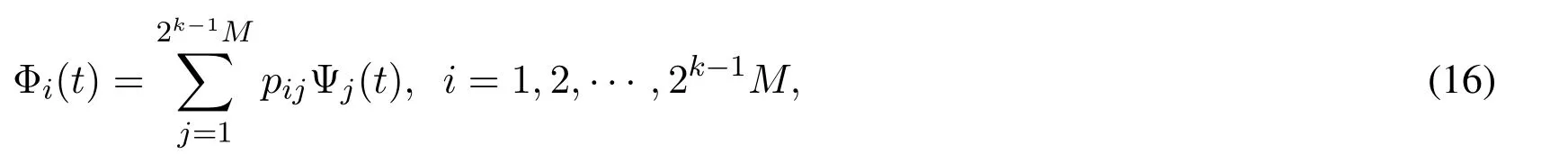
where

Φ(t)=[Φ1(t),Φ2(t),...,Φ2k-1M(t)]T=[φ10(t),φ11(t),...,φ2k-1(M-1)(t)]T.

Then,the following result is obtained:

whereP=[pij]is calculated by the means ofCin Eq.(14).

4.2 Transformation of differential operators

In order to numerically solve the variable order fractional differential equations,we propose to transform both integer and fractional order differential operators into matrix forms.

First,the following equation can be easily obtained for the first order differential operator:

where

and the number ofHin matrixSisn.Using(17)-(18),the following equation is derived

Second,using Eq.(5)the following equation can be obtained for the variable order fractional differential operator:

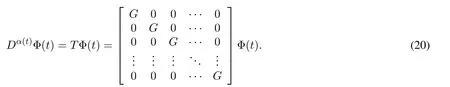
where

The number ofGin matrixTisn.Using(17)and(20),the following equation is derived:

whereQis the variable order fractional differential operational matrix of Euler wavelets.

5 Method of numerical solution

Consider the nonlinear variable order fractional differential equation

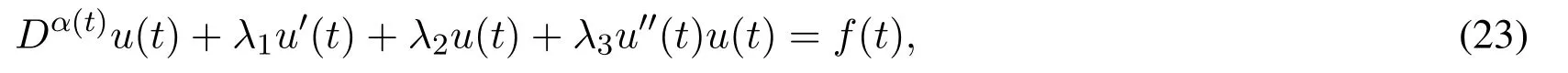
subject to initial conditionsu(0) =u0,wheref(t)∈L2[0,1]is known,u(t)∈L2[0,1]is the unknown function which we want to approximate,λ1,λ2,λ3andu0are all constants.Ifλ3is equal to 0,the equation reduces to linear case.

Now we approximateu(t)in terms of Euler wavelets as follows

Using Eq.(19),we have

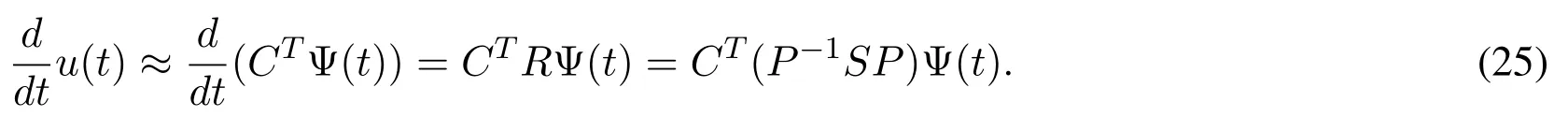
By combining(10)with(22),the following result is obtained:

Finally,Eq.(23)can be rewritten into the following matrix form:

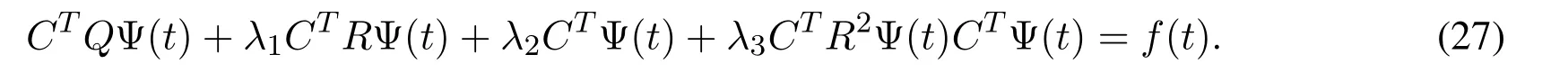
Then,by takingfori= 1,2,...,2k-1Mand solving the equations,we can obtain the unknownCby solving a system of algebraic equations.

6 Numerical examples

In this section,two examples are given to demonstrate the applicability and accuracy of our method.

Example 1.Consider the following linear variable order fractional differential equation:

where-90t-95,and the initial condition is equal tou(0) = 5.The exact solution of this equation is given byu(t) =5(1+t)2.By applying the proposed method withk=1,2,M=2,the numerical solutions can be obtained.Tab.1 shows the numerical errors obtained by Euler wavelets (Euler),Legendre wavelets(Leg)and finite difference scheme(FDS)[Chen,Wei,Liu et al.(2015)]respectively.In fact,for Legendre wavelets,the basis functions are not wavelets functions,but normalized Legendre polynomial whenk= 0.Similarly,for Euler wavelets,they are no longer the wavelets functions but the Euler polynomials whenk= 1.From Tab.1 we can see,the polynomials functions and the wavelets functions have the same error order with the sameM,but the coefficient matrix obtained by wavelet decomposition is sparse,which can greatly reduce the calculation amount and reduce the storage space.However,the polynomials basis functions have not such advantages.Meanwhile,The comparisons between approximate and exact solutions for variouskare shown in Fig.1.The numerical results forare shown in Tab.

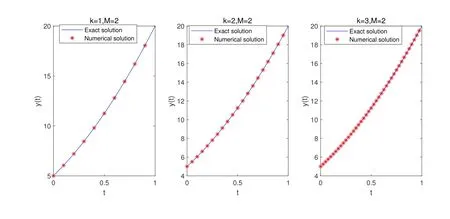
Figure 1:The approximate solution of Example 1 for different k

2.The absolute errors in Tab.2 corresponding to differentα(t)indicate that the numerical solutions are in good agreement with the exact values.

Table 1:Numerical errors for Example 1

Table 2:The absolute errors of different α(t)for Example 1

Example 2.Consider the following nonlinear variable order fractional differential equation:

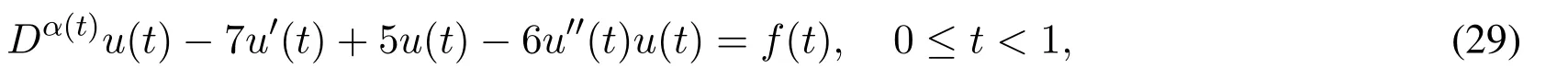
whereand

The exact solution of this equation isu(t) = 5(3t+t2).Then,by applying the proposed

Figure 2:The approximate solution of Example 2 for different k

method withk= 1,2 andM= 2,the numerical solutions can be obtained.Tab.3 shows the numerical errors obtained by Euler wavelets(Euler),Legendre wavelets(Leg)and finite difference scheme (FDS) [Chen,Wei,Liu et al.(2015)] respectively.The comparisons between approximate and exact solutions for variouskare shown in Fig.2.The numerical results forα1(t)are shown in Tab 4.

Table 3:Numerical errors for Example 2

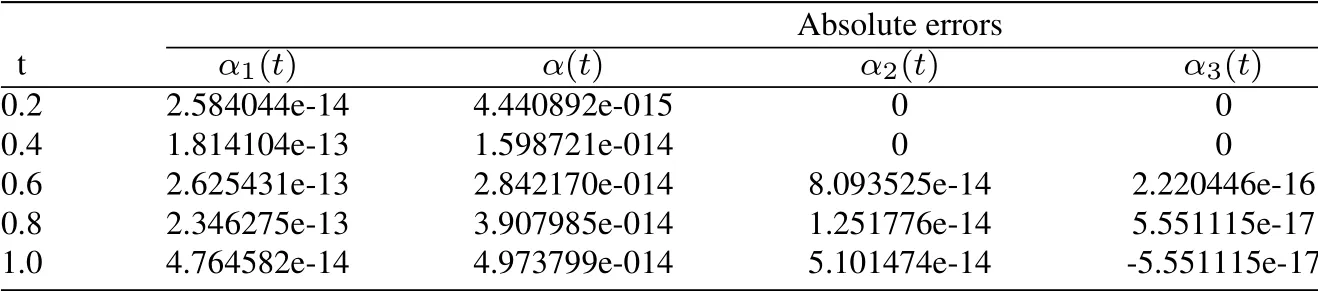
Table 4:The absolute errors of different α(t)for Example 2

According to the numerical examples,the numerical solutions obtained via Euler wavelets method have better accuracies than by Legendre wavelets and finite difference methods.Since Euler wavelets functions and the new functions are both constructed based on polynomials of commensurate degrees and also have a similarity on their forms,the derived operational matrices are quite accurate.Therefore,due to the uniform convergence of Euler wavelets functions,satisfactory approximation of exact solution could be found by appropriately choosingkandM.

7 Conclusion

A general formulation for the Euler wavelets operational matrix of variable order fractional order differential has been derived.This matrix is used to approximate numerical solutions of variable order fractional differential equations.Numerical examples are given to illustrate the powerfulness of the proposed method.Moreover,the achieved results are compared with the exact solution and the solutions derived by other approaches presented in open literatures,which further demonstrate the effectiveness of the presented method.

Acknowledgement:The authors are grateful to the editor,the associate editor and the anonymous reviewers for their constructive and helpful comments.This work was supported by the Zhejiang Provincial Natural Science Foundation of China(No.LY18A010026),the National Natural Science Foundation of China (No.11701304,11526117),Zhejiang Provincial Natural Science Foundation of China(No.LQ16A010006),the Natural Science Foundation of Ningbo City,China(No.2017A610143),and the Natural Science Foundation of Ningbo City,China(2018A610195).