Dynamic Response of Floating Body Subjected to Underwater Explosion Bubble and Generated Waves with 2D Numerical Model

Zhaoli Tian ,Yunlong Liu , ,Shiping WangA Man Zhang and Youwei Kang

Abstract: The low frequency load of an underwater explosion bubble and the generated waves can cause significant rigid motion of a ship that threaten its stability.In order to study the fluid-structure interaction qualitatively,a two-dimensional underwater explosion bubble dynamics model,based on the potential flow theory,is established with a double-vortex model for the doubly connected bubble dynamics simulation,and the bubble shows similar dynamics to that in 3-dimensional domain.A fully nonlinear fluid-structure interaction model is established considering the rigid motion of the floating body using the mode-decomposition method.Convergence test of the model is implemented by simulating the free rolling motion of a floating body in still water.Through the simulation of the interaction of the underwater explosion bubble,the generated waves and the floating body based on the presented model,the influences of the buoyancy parameter and the distance parameter are discussed.It is found that the impact loads on floating body caused by underwater explosion bubble near the free surface can be divided into 3 components:bubble pulsation,jet impact,and slamming load of the generated waves,and the intensity of each component changes nonlinearly with the buoyance parameter.The bubble pulsation load decays with the increase in the horizontal distance.However,the impact load from the generated waves is not monotonous to distance.It increases with the distance within a particular distance threshold,but decays thereafter.

Keywords:Underwater explosion,bubble dynamics,fluid-structure interaction,double-vortex model,waves generated by underwater explosion.

1 Introduction

The underwater explosion load is one of the crucial topics in the study of warship strength.In previous studies,shock wave and explosion bubble have received more attentions,and plenty methods are proposed to solve these problems [Zhang,Wu,Liu et al.(2017);Chen,Qiang and Gao (2015);Liu,Zhang and Tian (2014);Wang,Chu and Zhang (2014);Wang (2013);Lee and Keh (2013);Barras,Souli,Aquelet et al.(2012);Grenier,Antuono,Colagrossi et al.(2009);Geers (1978);Cole (1948)].The underwater explosion shockwave is so short that usually induces the high frequency responses of the structure and cause local structure failure.During this phase,the compressibility of the fluid must be considered to simulate the propagation of the shockwave and the radiation effects of the structure.The bubble load with long period can induce the overall whipping responses and the rigid motion that threaten the global strength [Zhang and Zong (2011);Stettler (1995);Hicks (1986);Vernon (1986);Wilkerson (1985)].For this problem,BEM based on potential flow theory is one of the most widely used methods,because the viscosity and the compressibility of the fluid are neglectable.Zhang et al.[Zhang and Zong (2011)] studied the dynamic responses of a surface ship subjected to underwater explosion bubble,and found that rigid motions cannot be ignored for shorter/wider hulls.Lu et al.[Lu,He and Wu (2000)] presented a completely coupled method for the hydroelastic interaction during the impact of a structure with water.There are some studies on the later phase showing that the underwater explosion near free surface can generate great waves [Torsvik,Paris,Didenkulova et al.(2010);Méhauté and Wang (1996)].If the waves are strong enough,they can impact the floating structure seriously.Although the interaction of waves and ships has been studied previously [Wang,Yeo,Khoo et al.(2005);Wu and Hu (2004)],the interaction between the ship structure and bubble generated waves is extremely rare.Because of the strong nonlinear interaction and the large ratios of dimensions in both space and time,many difficulties have to be overcome.Thus,there are only few published papers available on the impact of both the underwater explosion bubble and its generated waves on the floating body,which is not consistent with the increasing urgency of relevant studies.

This paper aims to discuss the nonlinear interaction between the underwater explosion bubble,generated waves,and floating body.BEM based on potential flow theory is used with the double-vortex model for the doubly connected bubble dynamics established in this paper.The convergence is verified by the ship roll theory,and the validity of the 2-dimensional (2D) bubble dynamics model is proved by comparing with the axisymmetric model.Then,the dynamic response of floating body subjected to underwater explosion bubble and generated waves is summarised by the discussion of the influence of buoyancy parameter and distance parameter.

2 Theoretical and numerical methods

Boundary Element Method (BEM) has been one of the most widely used methods in underwater explosion bubble dynamics and the wave-body interaction because of its advantages in accuracy,efficiency and interface tracking [Liu,Wang and Zhang (2016);Liu,Wang,Wang et al.(2016);Zhang and Liu (2015);Li,Zhang,Wang et al.(2018);Wang and Blake (2010);Wang,Yeo,Khoo et al.(2005);Klaseboer,Huang,Wang et al.(2005)].However,when the studied fluid field involves change of the field topology,special numerical treatments must be used to remesh the field boundary,such as the progress that a bubble bursting at a free surface and generating waves.In conventional 3-dimensional (3D) BEMs,the numerical treatments are too complex to code.Besides the ship is usually so slender that the variation of fluid field variables along the longitudinal direction is very small during the interaction of the bubble,free surface,and surface ship.Thus,the model can be simplified as 2D at the transverse section of the ship with the qualitatively consistent dynamics compared with the axisymmetric case.Although the 2D model is imaginary for the underwater explosion bubble,the dynamics and characteristics of pulsation,jet,and the interaction between the bubble and various boundaries are similar to the axisymmetric model,which will be proved later in this paper.Consequently,the 2D model presented here is used for the qualitative analysis.

2.1 Boundary integral equation (BIE)for bubble dynamics

The coordinate system is established as shown in Fig.1,with its origin located at the floating centre of the structure on the free surface and thezaxis pointing to the direction opposite to that of the gravitational acceleration.Here,handdare the initial depth of the bubble and the horizontal distance between the bubble and floating body,respectively.

Figure 1:Interaction between an underwater explosion bubble and a floating structure

Because the surrounding fluid flow caused by the underwater explosion bubble is a typical flow with high Reynolds number and low Mach number,it is reasonable to simplify the fluid as an incompressible one and the flow as inviscid [Klaseboer,Huang,Wang et al.(2005);Klaseboer,Khoo and Huang (2005);Wang (2004);Rungsiyaphornrat,Klaseboer,Khoo et al.(2003);Best (2002)].Thus,the problem is analysed using the potential theory,with the fluid potentialφsatisfying the Laplace equation

LetGdenote Green’s function.Then,using Green’s second identity,the fluid boundary potentialφsatisfies the boundary integral equation as follows:

where p and q are the field point and source point,respectively.Sdenotes all the boundary surfaces of the fluid field.The unit normal vector of which is expressed by n pointing inward to the closed flow field.For 2D problems,λstands for the solid angle denoted as:

whereScis part of an infinitesimal circle inside the fluid domain with its centre located at P.By discretising the free surface and bubble boundary into elements and nodes,Eq.(2) can be expressed in matrix form [Zhang and Liu (2015);Rungsiyaphornrat,Klaseboer,Khoo et al.(2003)]:

where G is the influence coefficient matrix corresponding to the first integral in Eq.(2).H is the influence coefficient matrix after the combination of the left solid angle and the second integral on the right equation.X and Φ are the column vector corresponding to the normal velocity and the velocity potential of the boundary nodes.The influence matrixes are determined by the geometrical features of the mesh.Either velocity potential or its normal derivative is known by introducing the boundary conditions,the linear equations can be solved.

2.2 Initial and boundary conditions

The solution of the equations above can be obtained only if sufficient initial and boundary conditions are provided.To solve the boundary integral equation,it is necessary to analyse the conditions corresponding to each research object after obtaining the initial conditions.The impenetrable condition for the rigid boundary,i.e.,the second boundary condition called the Neumann boundary condition,can be described as the known normal derivative of velocity potential and unknown velocity [Klaseboer,Huang,Wang et al.(2005);Koo and Kim (2004)].The following equation can be obtained based on the kinetic boundary condition:

where v is the velocity of the structure boundary which can be obtained by the kinematic function of the rigid body or the structural dynamics theory.

The boundary condition of the bubble and the free surface are given by the Dirichlet boundary condition,which can be expressed as the unsteady Bernoulli equation:

wherezis the vertical coordinate of the point of interest,andg,ρ,andPare respectively the gravitational acceleration,fluid density,and fluid boundary pressure,which is equal to eitherPatmat the free surface orPbat the bubble surface.The inner gas is assumed to be adiabatic because the duration of the bubble is relatively short for thermal transmission [Wang,Zhu,Cheng et al.(2014);Wang and Khoo (2004);Wang,Khoo and Yeo (2003);Best (2002)].Thus,the pressurePbcan be expressed as:

where,V0andVmare the initial and maximum volume of the bubble,respectively.γis the ratio of the specific heat,which is taken as 1.25 for the gas production of TNT.

As for the initial condition,the bubble is assumed to be still initially in the water.If the bubble expands spherically,the velocity of the flow field at the instant the bubble reaches its maximum volume is 0 so that the kinetic energy of the fluid field around the bubble is also 0.Thus,the work done by the inner gas on the fluid outside the bubble is equal to the change of its kinetic energy,which is zero specifically,

here,R0andRmare the initial and the maximum bubble radius.S(r) is the area of the bubble.Substitute Eq.(7) into Eq.(8) we have,

By solving Eq.(9),the equation forP0,V0,andVmis obtained as:

Then,there is always an initial pressure corresponding to the initial and maximum volume.In the same way,if the initial pressure is known,there is an initial volume satisfying Eq.(9) in a reasonable range.Then,the equation is solved by a suitable nonlinear equation solver such as Newton’s method.As for the underwater explosion bubble,two additional equations can be obtained by some empirical formula [Klaseboer,Huang,Wang et al.(2005);Best (2002);Cole (1948)]:

Here,Rmis the maximum radius;kRandkpare experimental coefficients,wherekR=3.38 andkp=1.39×105for the TNT explosive.By combining Eqs.(10)-(12),the initial pressure and volume of the underwater explosion bubble can be determined based on the explosive weightWand depthh.As for the 2D model,the same initial pressure and volume as those of the axisymmetric model are used in this study.The initial radius can be obtained for the 2D model by solving the nonlinear equation.

2.3 Double-vortex model for the doubly connected bubble dynamics

The fluid flow transforms from simply connected to doubly connected when the jet penetrates the bubble.Thus,the velocity potential of the flow field is no longer a single-valued function for the spatial coordinates,and it cannot be solved by the conventional BEM.The vortex ring model is the prevalent approach in previous studies

[Wang,Yeo,Khoo et al.(2005);Zhang,Yeo,Khoo et al.(2001);Wang,Yeo,Khoo et al.(1996a)].Assuming that the jet impacts the bubble wall starting from a single point,the increase in velocity potential at the penetrating point has a specific value.Then,through the configuration of a certain intensity vortex ring,the velocity of the flow field u surrounding the toroidal bubble can be decomposed into velocity induced by the vortex ring and residual velocity ures[Wang,Yeo,Khoo et al.(2005);Zhang,Yeo,Khoo et al.(2001);Lundgren and Mansour (1991)]:

In a similar way,the velocity potential of the fluid flowφcan be also decomposed into velocity potentialφvrinduced by the vortex ring and residual velocity potentialφres:

The residual velocity potentialφresis continuous in the entire fluid domain,which satisfies the Laplace equation and boundary integral equation.Hence,it can be solved as follows.First,the residual normal velocity of nodes is obtained by solving the boundary integral equation.Second,the residual velocity is calculated.Third,the resultant velocity is obtained by adding the residual and induced velocities.

The residual velocity potential can be updated using Eq.(15):

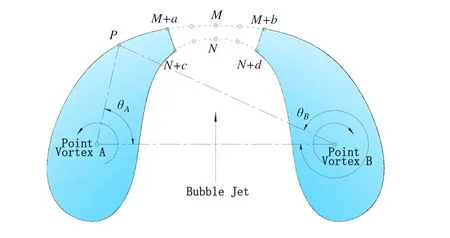
Figure 2:Double-vortex model for penetrated 2D underwater explosion bubble

In contrast with the toroidal bubble in axisymmetric model,there are two independent bubbles in the 2D model after jet penetration,and two vortexes instead of the original vortex ring,i.e.the double-vortex model,is proposed in this study.Clearly,in order to satisfy the same velocity integral regardless of the path from impact pointMtoN,it is necessary to ensure that the double vortexes have an equal value and opposite orientation,as shown in Fig.2.

The induced velocity is calculated using Eq.(16):

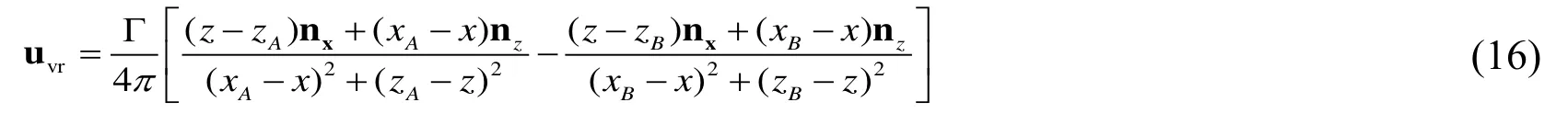
wherexA,zA,xB,zB,andx,zare the coordinate components of point vortex A,B,and the point of interest;nxand nzare the unit normal vector of axisxand axisz,and Γ is the intensity of the point vortex.The induced velocity potential can be expressed by Eq.(17):

whereθAandθBare as shown in Figure 2.To ensure that the residual velocity potential is a continuous function after introducing the point vortexes,it is necessary to let the velocity potential jump at the location affected by the point vortexes,which is equal to the balance of velocity potentials of the two sides of the jet impacting point,as given by Eq.(18):

whereφMandφNare the velocity potentials at pointMand pointN;then,the velocity induced by the double vortexes can be obtained if we substitute Eq.(18) into Eq.(16).The reference angle forθAandθBis required to determine if Eq.(17) is adopted.Hence,it is always necessary to adopt other approaches,for example,an arbitrary curve L can be introduced to connect the two point vortexes;then,the velocity potential of field point p induced by the vortexes can be obtained by calculating the solid angle of point p from curve L:

Theoretically,the exact locations of the point vortexes are not important as long as they are inside the bubbles.However,a small distance between a point vortex and bubble surface will result in a significant error in the numerical integration induced by the singularity and the simulation instability.Hence,it is necessary to update the location of the vortexes along with the deformation of bubble surface during the simulation.The exact arrangement method can be referred to the previous study [Zhang and Liu (2015)].

2.4 Fluid-structure interaction model

The problem of warship structures impacted by underwater explosion bubble and its generated waves is a typical fluid-structure interaction problem.It must be solved considering the bidirectional influences.To solve the interaction problem,some implements of the bubble and free surface model are illustrated in the foregoing parts,and the fluid-structure interaction implementation is presented as follows.

Because the transverse stiffness in the studied problem has a higher structure shock frequency compared with the outside excitation from the waves generated by the bubble,the resilience of the structure can be ignored and the structure can be assumed as rigid.The configuration of the coordinate system for the structure motion is shown in Fig.1.The rigid motion of the structure can be decomposed into sway motion along axisx,heave motion along axisz,and rolling motion in thexozcoordinate plane.

Following the existing research [Koo and Kim (2004);Tanizawa (1995)],the normal velocity of the nodes on the rigid structure surface,i.e.the nodes on the surface of the fluid-structure interaction,can be expressed by introducing an acceleration potential Φ.

The relationship between the acceleration potential and velocity potential is obtained by exploiting the relationships between the velocity and velocity potential of fluid flow nodes and that between the acceleration and derivative of velocity as given by Eq.(20):

The equation of the acceleration potential above contains both linear and nonlinear terms.There is only one linear termφtsatisfying the Laplace equation,which can be solved by the boundary integral equation as indicated in Eq.(21):

In order to solve Eq.(21),the mode-decomposition method is adopted.Based on the accelerations of sway,heave,and rolling motion and the acceleration generated by the velocity field,φtcan be decomposed into four modes as given in Eq.(22):

whereaiand φidenote the acceleration and velocity potential of theith mode,respectively,andi=1,i=2,andi=3 are for the sway motion,heave motion,and rolling motion respectively;φ4is the acceleration potential for the diffraction motion.Then,the acceleration potential φion the wet surface of the structure can be determined using the following boundary conditions.The boundary condition of the free surface is given in Eq.(23):

The boundary condition of the bubble can be expressed as Eq.(24):

Eq.(21) can be solved by obtaining the valueof the wet surface of the floating body as indicated in Eq.(23);then,the valuesof the free surface and bubble surface can be obtained:

whereBκdenotes the contribution of velocity field to the acceleration field;niare the components of unit rigid motion in the ith degree projecting to the direction of n,

wherexRandzRare the 2 components of R which denoting the vector from the rotation center to point p;exand ezare the unit vector in thexandzdirections,respectively;i=1,2 correspond to the translational degrees in thexandzdirections,respectively;i=3 corresponds to the rotational degree of the floating body.

To determine the acceleration of each mode,the hydrodynamic force can be obtained by integration of the pressure at the wet surface expressed by Eq.(28):

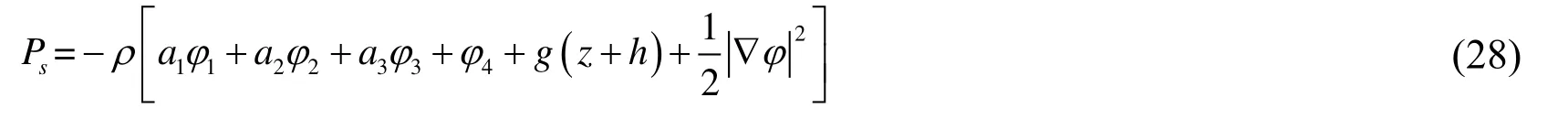
wherePsstands for the hydrodynamic pressure on the floating body.Then the equilibrium equation of the resultant force at theithdirection can be written as:

whereBspresents the surface of the floating body;Ixxis the moment of inertia of the floating body.Rewrite Eq.(29) in the matrix form:

where,A and F are the column vector of the acceleration and external force independent with the acceleration,respectively;M is the diagonal mass matrix;Mais the added mass matrix.F and Maare defined as

respectively.By solving the equation above,the accelerationaiof each mode can be obtained.Furthermore,the derivative of the velocity potential can be solved.The velocity of the structure,motions of sway,heave,and roll can be obtained by the 4th order Runge-Kutta method,and the new geometrical location of the structure for the next time step can be adopted.Thus,the strategy of the modelling can be expressed as the flow chart in Fig.3.

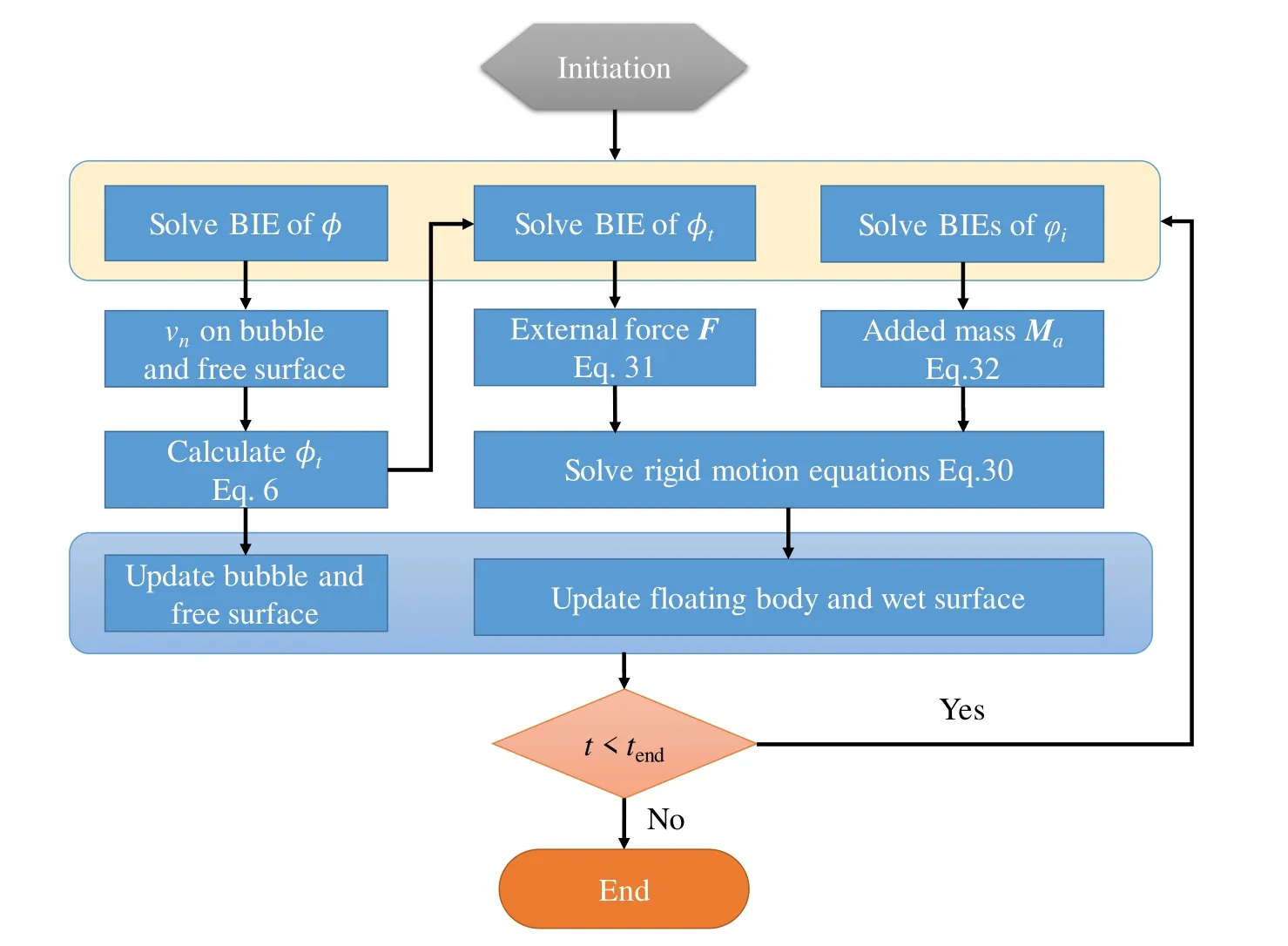
Figure 3:Flow chart of the numerical model for the interaction of underwater explosion bubble,generated wave and floating body

2.5 Non-dimensionalization

For convenience of generalisation,all variables are non-dimensionalized with the breadthBof the ship,fluid densityρ,and hydrostatic pressureP∞at the depth of the initial bubble [Klaseboer,Huang,Wang et al.(2005);Zhang and Liu (2015)].Then,the non-dimensional scales for the mass,moment of inertia,velocity,and time areρB3,ρB5,andrespectively.Hence,the Bernoulli equation of the flow field in its dimensionless form is given below:

3 Model verification

3.1 Comparison between 2D and axisymmetric bubble dynamics

To verify the qualitative equivalence between the 2D and axisymmetric bubble dynamics models [Wang,Yeo,Khoo et al.(1996b)],the evolution of the bubble and the free surface are simulated with the presented 2D model and the conventional axisymmetric model with the same initial conditions,where ε=100,H=0.5,andδ=0.92.

Fig.4 indicates that during the shrinking phase of the bubble,the upper part of the bubble in each case develops a downward jet owing to the Bjerknes force of the free surface,while the bottom bubble generates an upward jet subjected to buoyancy.Simultaneously,the spike of the free surface becomes thinner and arches as a water column.Obviously,the dynamics in the 2D model is similar to that in the axisymmetric model in spite of the differences in the sizes of the spike and downward jet.This is because the infinite cylindrical bubble represented by the 2D model amplifies the interaction between the bubble and the free surface,resulting in a higher and thinner spike and downward jet.Thus,the 2D model is suitable for the qualitative analysis of the studied problem.Moreover,the 2D model has irreplaceable advantages in efficiency and handling of the breaks of the free surface and the bubble compared with the 3-D model.Thus,the 2D model is used in this study.

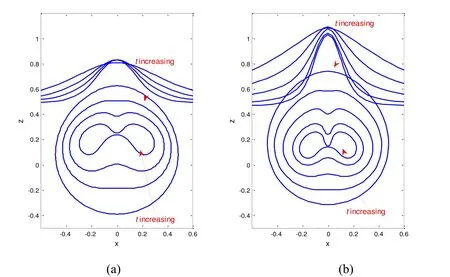
Figure 4:Evolution of bubble and free surface shapes during the collapse phase for H=0.5,ε=100 and δ=0.92:(a) axisymmetric model [Wang,Yeo,Khoo et al.(1996b)] results at t=0.44,0.61,0.69 and 0.75;(b) 2D model results at t=0.70,0.91,1.03,1.11 and 1.16

3.2 Convergence test of the fluid-structure interaction model

In order to validate the theoretical model described in Section 2,the free rolling motion of the floating body is simulated,and the results are compared with those of analytical solutions.

In the simulation,the floating body is chosen as a 1×1 square with two filleted corners,and the fillet radius is 0.25.The draft of the floating body is 0.45,and the moment of inertiaIxxis 0.093.The floating body and the free surface are discretised into 60 and 300 linear elements.The simulation starts with the floating body released from rest,and the initial heel angle is 0.15.Subsequently,the floating body rolls because of the restoring moment from the water.

According to the ship rolling theory,the rolling motion period of the floating body without damping effect is given by:

whereDis the tonnage of the ship,h*is the initial metacentric height,Ixxis the moment of inertia,andJxxis the added moment of inertia,which can be expressed as:

The simulation results at different time increments are compared in Fig.5.

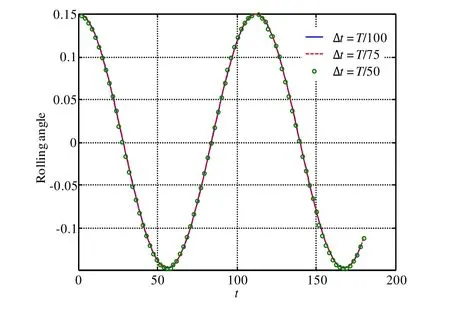
Figure 5:Convergence test of numerical model

From the curve,we can observe that the results are not sensitive to the time increment in the chosen parameter range,which indicates good convergence of the numerical model.The rolling period of the floating body is 111.6,which is 0.26% smaller than the empirical result of 111.9.In the simulation below,the time increment Δtis set as less thanT/50.

4 Numerical results and discussion

4.1 Primary phenomenon discussion

Based on the verified model described in the preceding section,we choose the following case parameters to simulate and analyse the interaction of the bubble,free surface and the nearby floating body:buoyancy parameterδ=0.14,intensity parameterε=100,distance parameterr=1.5,and initial radius parameterR0=0.0446.

4.1.1 Discussion on bubble dynamics

Fig.6 and the following figures of the same kind show the motions of the bubble,free surface and floating body before jet penetration.The colour contours stand for the different dimensionless pressure and the arrow arrays indicate the velocity.

In Figs.6a-6c,the floating body begins to move toward the upper right with a little clockwise slope under the effect of bubble load.In addition to the hump on the free surface above the bubble,a smaller hump emerges near the fluid-structure interaction during the bubble expansion.The pressure inside the bubble is low as the bubble achieves its maximum volume and it radiates negative pressure to the field.In Figs.6d-6f,during the bubble shrinking phase,the negative pressure region extends from the bubble to the lower surface of the floating body,and the free surface between the hump and the interaction point hollows rapidly stimulating a huge cavity.As a result,an anticlockwise restoring moment is produced owing to the decrease of buoyancy at the left side of the floating body.The hump near the fluid-structure interaction keeps growing simultaneously under the action of the high-pressure region between the bubble and free surface;thus,there is an independent liquid drop forming and breaking away from the flow field.The liquid drop is so small that the re-entry effects on the field can be ignored.

Figure 6:Interaction between the bubble and floating body before jet penetration at t=0.00,0.20,0.98,1.57,1.75 and 1.89.The colour contour and the arrows represent the pressure and the velocity of the field

When the bubble is penetrated by the jet,it is split into two independent bubbles,and the flow field is transformed into a doubly connected field as shown in Fig.7.

At the instant when the bubble is penetrated by the jet,there is a high-pressure region forming near the impact point.The new independent bubbles keep shrinking until they reach their minimum volumes.Because the cavity of the free surface isolates the floating body from the bubble,the second pulsation pressure from the bubble barely affects the floating body.Then,the new bubbles begin to rebound,and a high-pressure region near the interaction point emerges,which causes the cavity of the free surface to collapse rapidly and subsequently impacts the floating body.

During expansion of the split bubbles,the liquid film between the two bubbles becomes thinner and thinner.When the film breaks,the two bubbles coalesce into a new simply connected bubble.The criterion for the film breaking is chosen as the thickness of the liquid film that is smaller than the average element length of the bubbles.

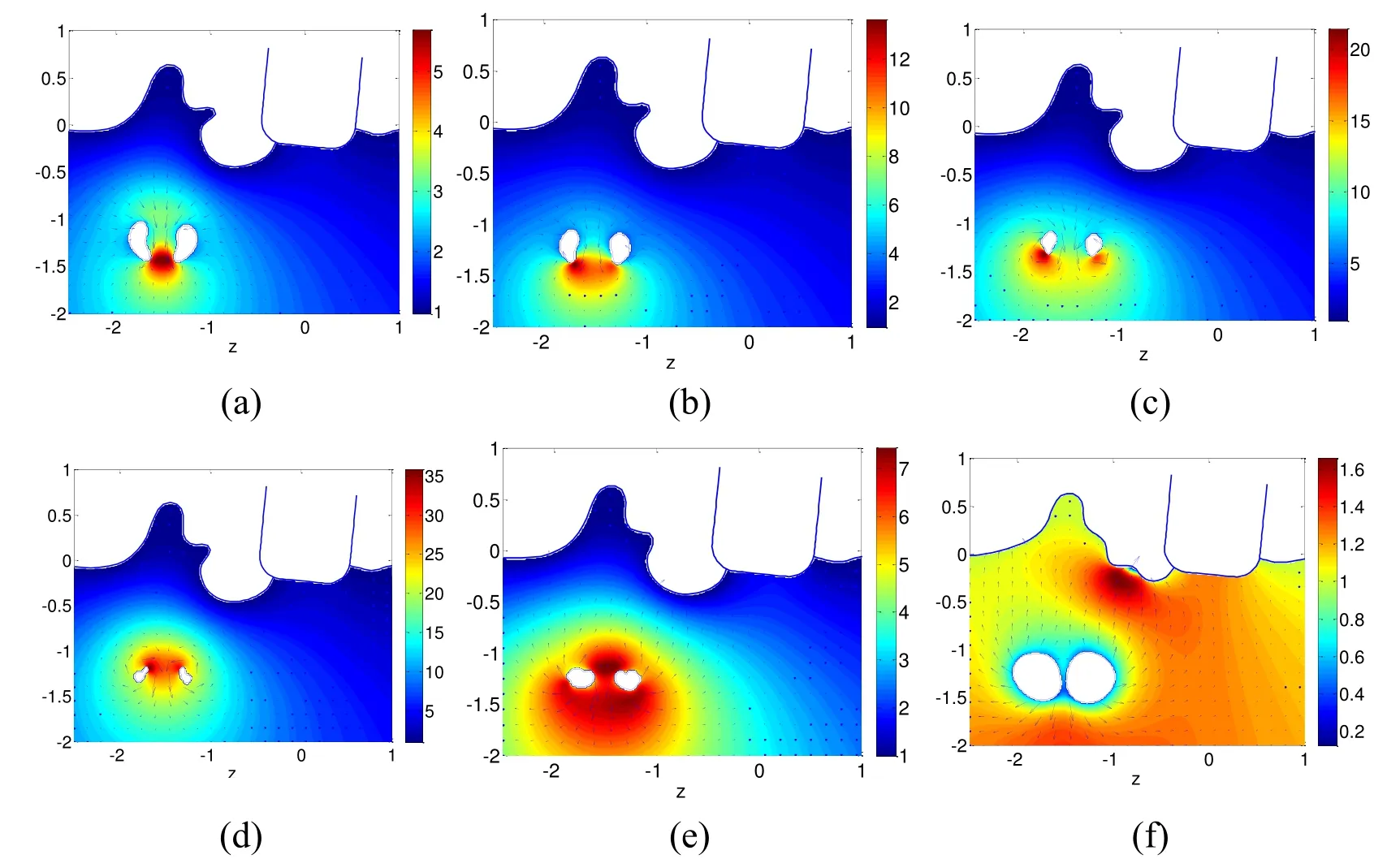
Figure 7:Interaction between the bubble and floating body after jet penetration at t=1.93,1.95,1.97,2.00,2.04 and 2.18.The colour contour and the arrows represent the pressure and the velocity of the field

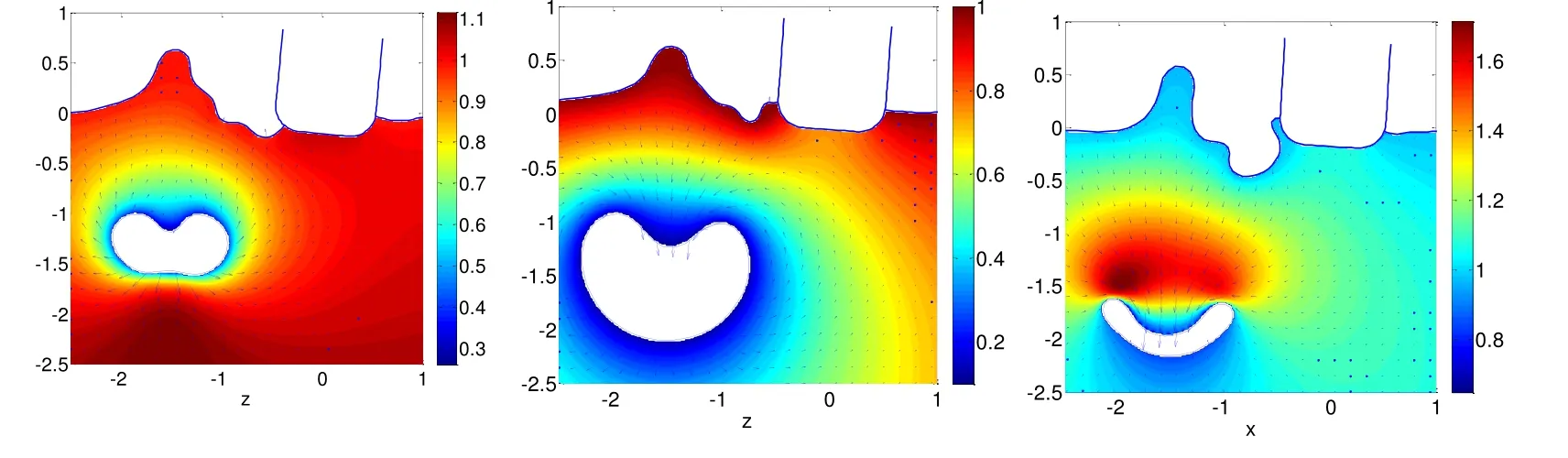
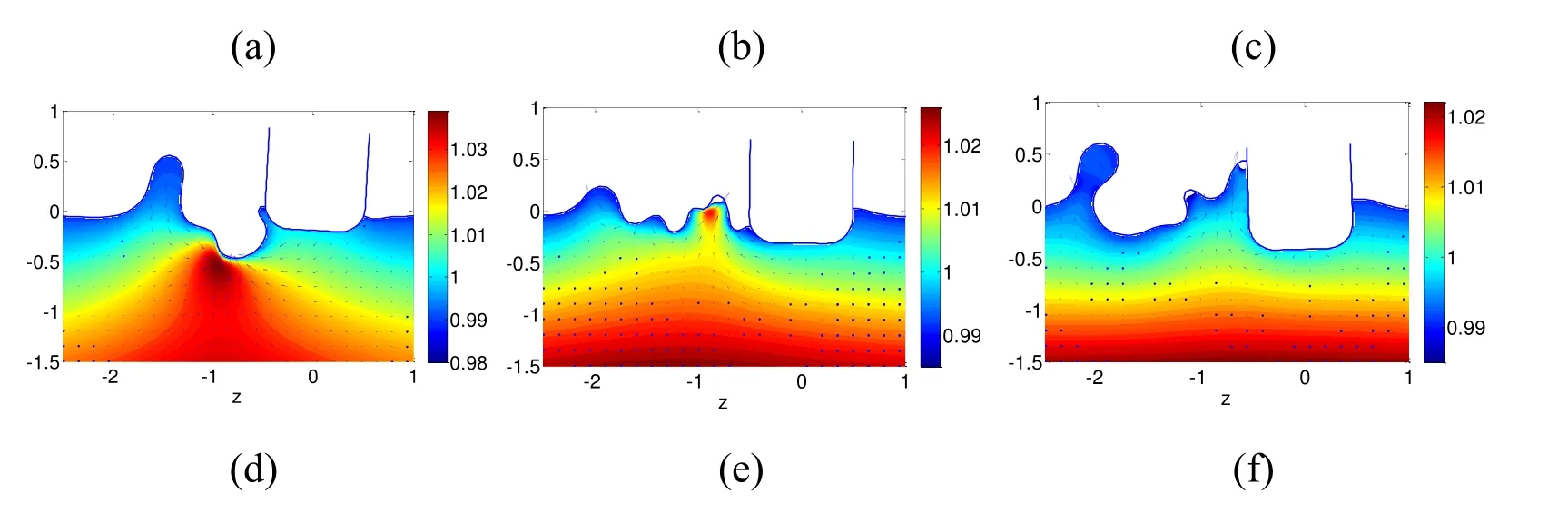
Figure 8:Interaction between the bubble and floating body after re-fusion at t=2.25,2.95,3.80,4.00,6.50 and 8.50.The colour contour and the arrows represent the pressure and the velocity of the field

The colour contours in Fig.8 represent the dimensionless pressure in the flow field when the two bubbles coalesce into one bubble.In Figs.8a-8c,the bubble after the coalescence keeps expanding and moving downward because of the repelling effect of the free surface,and subsequently reaches its maximum volume.Then,the second downward jet emerges during its shrinking phase and will penetrate the bubble again.A large amount of bubble energy is consumed during every pulsation,and the distance from the free surface is increasing simultaneously.Thus,the disturbances on the free surface and the floating body caused by the bubble are extremely small that the effect can be ignored,as shown in the pressure nephogram in Figs.8d-8f.In such cases,the initial bubbles induced mainly by the free surface during the previous pulsations always move downward.When the bubbles begin to move up after most of the energy is consumed,they burst into many smaller bubbles that cannot generate appreciable waves and can be ignored.Thus,to simplify the computation,the small bubbles are removed from the flow field.

4.1.2 Analysis of the motion of the floating body

As shown in Figs.6-8,the floating body exhibits serious rigid motion subjected to the bubble load.The histories of the displacements in directions ofx,zandωare shown in Fig.9.

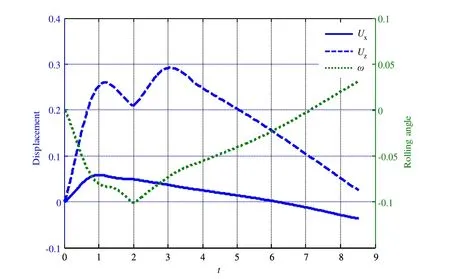
Figure 9:Rigid motion curves of the floating body

During the initial bubble expansion phase,the floating body moves to the upper right under the influence of the bubble,while it is attracted to move back during the bubble shrinking phase.The floating body moves upward rapidly when the bubbles reach their minimum volumes and radiate the second pulsation load after the first jet penetration.Because of the existing free surface cavity at the bottom left of the floating body,the horizontal movement of the structure is not affected by the second pulsation load.

4.2 Influence of buoyancy parameter

Compared with the case withδ=0.14,the buoyancy parameter in this case is set asδ=1.0,which can be classified as a large buoyancy parameter case.The other parameters remain the same as in the case discussed above.

4.2.1 Discussion on bubble dynamics

During the initial bubble expansion phase,the variation of the fluid flow is similar to that of the small buoyancy parameter case.The shrinking phase is shown in Figs.10d-10f.Because the buoyancy is obviously larger than the free surface effect,the bubble motion is mainly influenced by the buoyancy.Under the driving effect of the high-pressure region below,an upward jet develops at the bottom of the bubble,and eventually penetrates the bubble.The motion of the free surface is similar to that of the small buoyancy parameter case;however,the cavity of the surface near the interaction point is apparently smaller than that of the previous case.This is because the cavity is generated by the inertial force from the bubble,which is larger than the free surface effect in this case.

Figure 10:Interaction between the bubble and floating body before jet penetration at t=0.00,0.20,0.85,1.30,1.50 and 1.60.The colour contour and the arrows represent the pressure and the velocity of the field

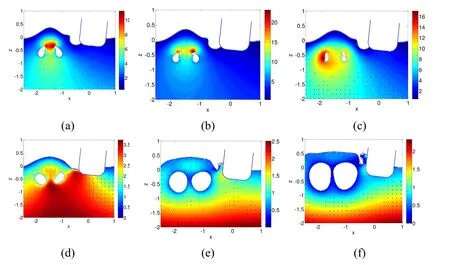
Figure 11:Interaction between two bubbles and the floating body after jet penetration at t=1.62,1.64,1.67,1.77,1.90 and 2.05.The colour contour and the arrows represent the pressure and the velocity of the field

As shown in Fig.11a,there is a high-pressure region developed near the jet impact position in the flow field after the jet penetration.When the two newly formed bubbles begin to expand,the cavity near the interaction point is restored by the effect of the high-pressure region and it produces an impact on the floating body,as shown in Fig.11d,which is clearly larger than that of the small buoyancy parameter case.Then,there is a splash generated on the free surface near the impact point,while the two bubbles expand to some extent and coalesce into a simply connected bubble.

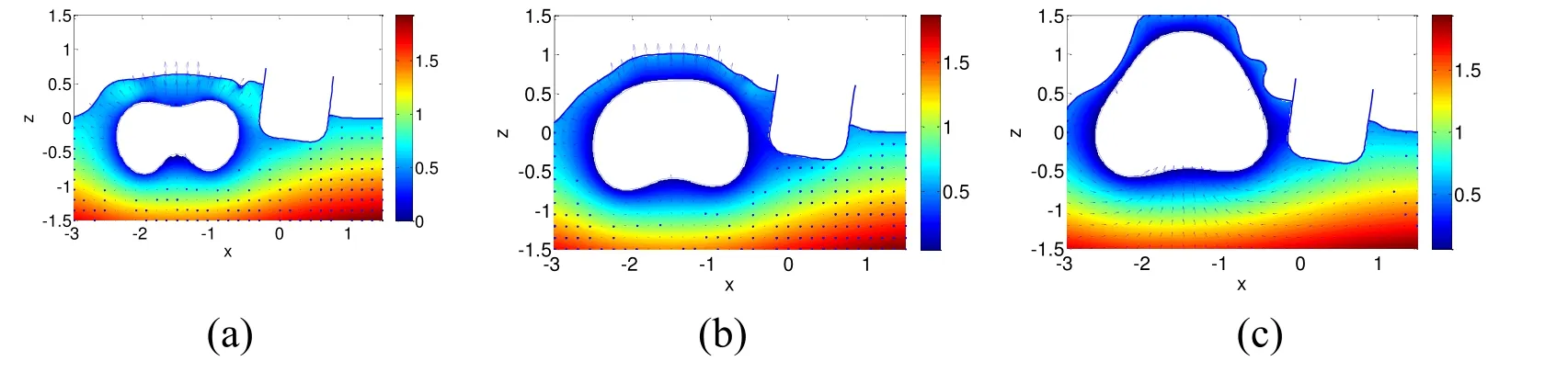
Figure 12:Interaction between the new single bubble and floating body after jet penetration at t=2.10,2.30 and 2.70.The colour contour and the arrows represent the pressure and the velocity of the field

In Fig.12,we can observe that the new simply connected bubble keeps expanding and moving upward,generating a huge spike on the free surface that pushes the floating body to heel to starboard.When the bubble is close to the free surface,the bubble will burst,and will generate a huge initial disturbance on the free surface as shown in Fig.13.

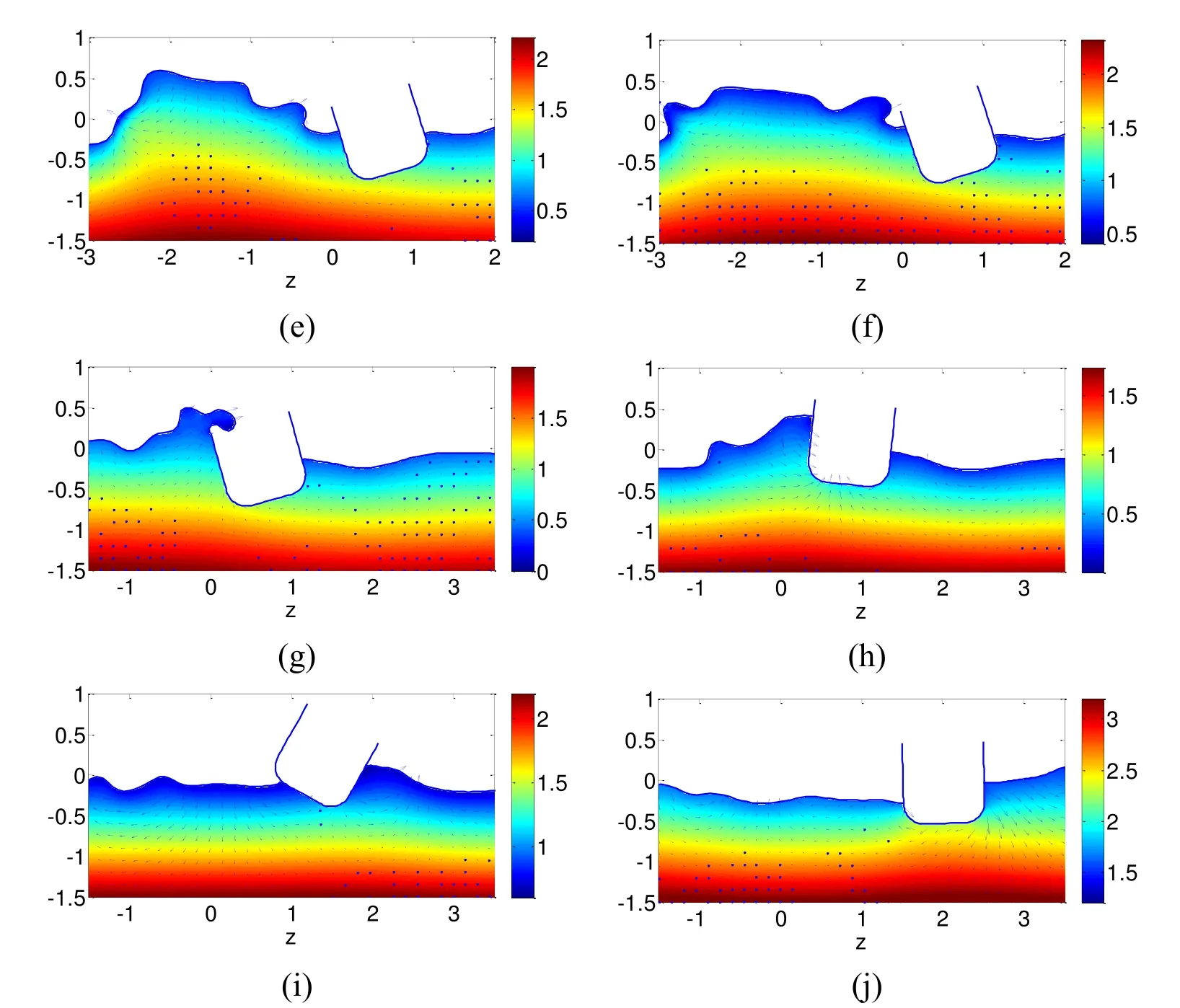
Figure 13:Interaction between the bubble and floating body after bubble bursting at t=3.13,3.60,4.60,5.00,5.50,5.75,6.20,7.20,8.50 and 10.50.The colour contour and the arrows represent the pressure and the velocity of the field

A huge cavity on the free surface appears after bubble bursting and will occupy the surrounding fluid.Then,because of the inertia of the fluid,the free surface keeps rising and becomes a huge water column as shown in Figs.13a-13c,the mechanism of which is similar to the jet development caused by the buoyancy effect.In Figs.13d-13e,the water column keeps rising until the kinetic energy entirely converts to potential energy,and then it begins to fall.During the falling process,the free surface on both sides of the water column is lifted rapidly and becomes a single curling wave propagating away from the water column.Because the initial distance from the explosion point is small,the generated waves have not fully developed when they reach the floating body.The waves impact the structure and cause it to heel to the right and move horizontally.Meanwhile,the floating body is lifted by the expanding wave and moves to the upper right,as shown in Figs.13e-13h.During the interaction between the solitary wave and floating body,we can observe in Fig.13g that the height of the wave is larger than that of the freeboard,which indicates that the deck of the floating body will be subjected to high water impact from the generated waves.As shown in Figs.13h-13j,the floating body will squeeze to the right side free surface and a solitary wave will develop and propagate to the right during the falling process of the floating body,which will consume a large amount of the structure’s kinetic energy.

From the foregoing discussions,the effect of the bubble on the floating body in the large buoyancy parameter case is weaker.However,the impact of the waves generated on the free surface is more severe when the bubble floats to the free surface and bursts,resulting in more violent rolling motion that threaten the safety of the floating body.

4.2.2 Analysis of the motion of the floating body

Fig.14 shows the time histories of motions of the floating body with large buoyancy parameter.During the early stage of the interaction (t＜3.0),the heave and rolling motion in this case are basically as the same as those of the case with small buoyancy parameter,while the horizontal motion is different.During the bubble shrinking phase,the floating body moves right away from the bubble with a smaller velocity,whereas it moves toward the bubble in the small buoyancy parameter case.The reason is that the floating body in this case is on the suitable slope of the spike,and the slope will offer a suitable component of buoyancy to the body,which will offset the negative influence of the fluid flow and cause the body to keep moving horizontally to the same direction.Att=3.13,the bubble bursts on the free surface and generates waves.Although the peak value of the wave load is smaller than the bubble pulsation pressure,the impact time on the floating body is as long as 2.5,as indicated in Fig.13,which is larger than the bubble pulsation period and less than a quarter of the natural rolling period.During this period,the rolling motion is more severe and the maximum rolling angle is as large as 30.

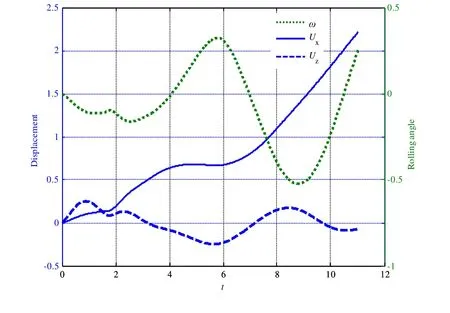
Figure 14:Time history of rigid body motion of the floating body

4.3 Influence of distance parameter

From the discussion above,we can observe that the bubble motion is mainly influenced by the buoyancy,while it is not sensitive to its effect on the floating body.However,under the impact of generated waves,the floating body moves more violently with a larger buoyancy parameter.In this section,we will discuss the influence of distance parameter on the rigid motion of the floating body.

We simulate two cases of interactions with different distance parameters.The case withr=2.0 as shown in Fig.15 is similar to that withr=1.5 as shown in Fig.13,where the red arrow indicates the time-marching direction.The main difference is that the main motions of the floating body after the effect of solitary wave are translations directed horizontally to the right and rolling motions,whereas the heave motion is as small as the increase in distance.

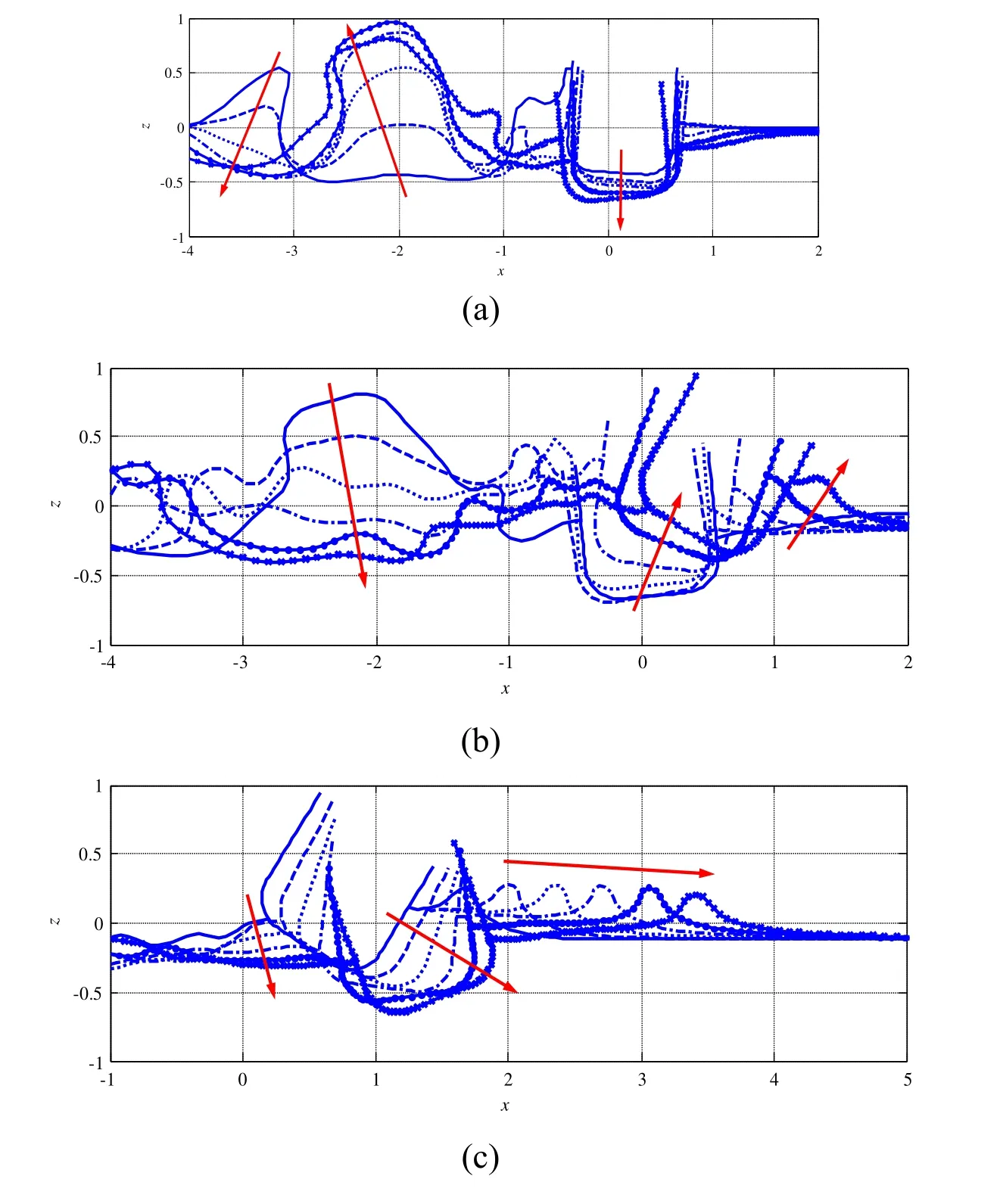
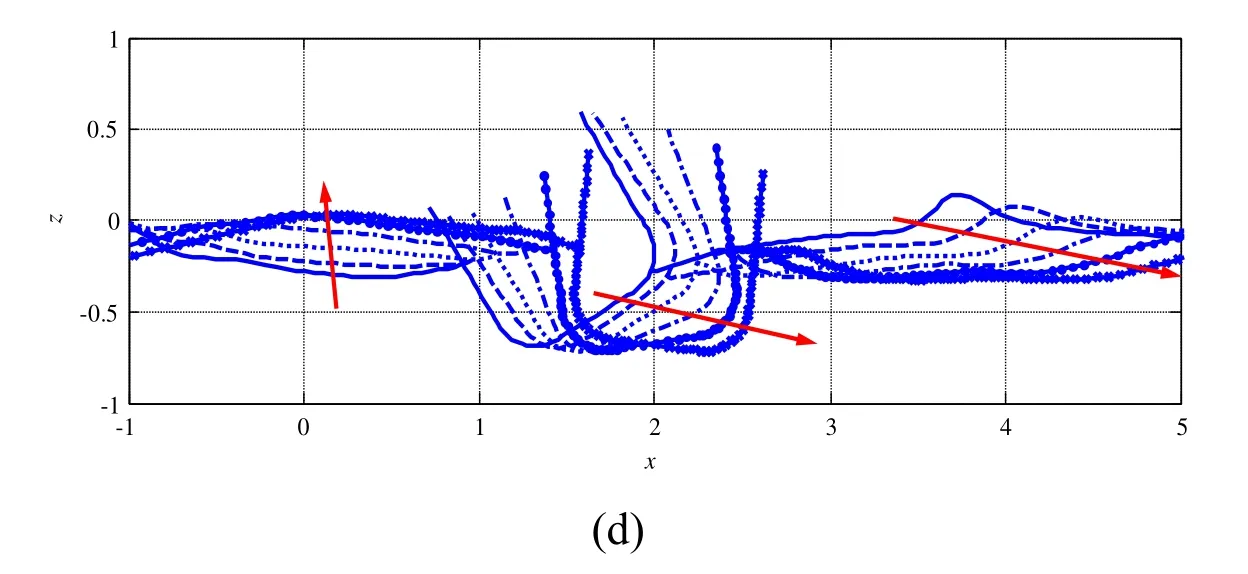
Figure 15:Interaction between the bubble and floating body after bubble bursting with r=2.0 at t=2.8,3.3,3.8,4.3,4.8,5.3,5.8,6.3,6.8,7.3,7.8,8.3,8.8,9.3,9.8,10.3,10.8 and 11.3.The arrows indicate the time increasing direction

Compared with the two cases,the rigid body motions withr=2.5 are more violent as shown in Fig.16.Under the impact of the solitary wave,there is a small heave motion for the floating body.Most of the slamming momentum from the waves converts to rolling motion of the floating body,which is more dangerous to the ship stability.

The influence of a pulsating bubble near the free surface of a fluid domain can be equivalent to that of a dipole under the linear free surface assumption.In the 2D cases,the influence of the fluid flow on the velocity potential caused by the dipole decays linearly along with the reciprocal of the distance.Considering the induced pressure is approximately proportional to the induced velocity potential,it is easy to obtain that the induced pressure is linearly related tor-1.

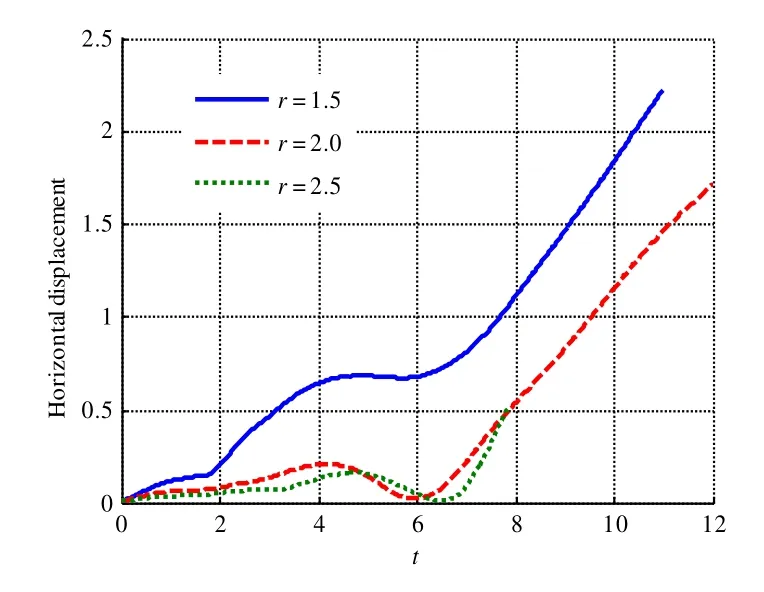
Figure 17:Comparison among horizontal displacements of different distances

Figure 18:Comparison among vertical displacements of different distances

Figure 19:Comparison among swing angles of different distances

Figs.17-19 show the comparison of the histories of the motions of the floating body for different distance cases.The comparison indicates that there are two development regions for the generated waves.The motion of the body under the influence of generated waves changes along with the distance parameter.At the early stage,the influence of the distance parameter is displayed as the difference in the peak values of the motions,while the motion styles are nearly the same.When the bubbles burst (at approximatelyt=2.8),the interactions become much more complex.Compared with the small distance parameter case,the rigid motion in the large parameter case decreases rapidly,and the floating body is lifted slightly and even capsizes owing to the solitary wave.Because it requires some time for the wave to propagate to the floating structure,there is a time delay for the violate motion induced by the wave impact as shown in the history curves.

5 Conclusions

In this study,a 2D underwater explosion bubble dynamics model is established with a double-vortex model for the doubly connected bubble dynamics simulation based on the potential flow theory.The evolution of bubble and the free surface is simulated successfully and shows similar dynamics to that in 3D domain.A fully nonlinear 2D fluid-structure interaction model is established considering the rigid motion of the floating body using the mode-decomposition method,whose convergence is provided by the comparison with the free rolling motion of the floating body.Thus,the models can qualitatively analyse the nonlinear interaction between the underwater explosion bubble,free surface,and floating body.Several conclusions are summarized as follows to serve as reference for anti-shock studies on warships.

The impact on warships caused by underwater explosion bubble near the free surface can be divided into three components,i.e.jet impact,bubble pulsation,and slamming load of the generated waves.Before the bubble burst,the rigid motion of the floating body is mainly determined by the inertia force represented by the bubble pulsation load,which is not obviously related to the buoyancy.However,the buoyancy plays a dominant role in the interaction between the floating body and the generated waves after the bubble bursting.Thus,in the large buoyancy parameter case,the stability of the body is more seriously threatened by the generated waves.

The bubble pulsation load decays with the increase in distance.However,the impact load from the generated waves increases with the distance within a particular distance threshold,and decays thereafter.

Acknowledgments:This work was supported by the National Natural Science Foundation of China (Grant No.51879050,51609044),the Defense Industrial Technology Development Program of China (Grant No.JCKY2017604C002),Natural Science Foundation of Heilongjiang Province of China (No.E2017021) and Shenzhen Special Fund for Future Industries (Grant No.JCYJ20160331163751413).

References

Barras,G.;Souli,M.;Aquelet,N.;Couty,N.(2012):Numerical simulation of underwater explosions using an ALE method.The pulsating bubble phenomena.Ocean Engineering,vol.41,pp.53-66.

Best,J.P.(2002):The Effect of Non-Spherical Collapse on Determination of Explosion Bubble Parameters.DSTO Systems Sciences Laboratory,Edinburgh,Australia,pp.1-25.

Chen,F.Z.;Qiang,H.F.;Gao,W.R.(2015):Numerical simulation of bubble formation at a single orifice in gas-fluidized beds with smoothed particle hydrodynamics and finite volume coupled method.Computer Modeling in Engineering ＆Sciences,vol.104,no.1,pp.41-68.

Cole,R.H.(1948):Underwater Explosion.Princeton University Press,USA.

Geers,T.L.(1978):Doubly asymptotic approximation for transient motions of submerged structures.Journal of the Acoustical Society of America,vol.64,pp.1500-1508.

Grenier,N.;Antuono,M.;Colagrossi,A.;Touze,D.L.;Alessandrini,B.(2009):An Hamiltonian interface SPH formulation for multi-fluid and free surface flow.Journal of Computational Physics,vol.228,no.22,pp.8380-8393.

Hicks,A.N.(1986):Explosion induced hull whipping.In:Smith,C.S.;Clarke,J.D.(Eds.),Advances in Marine Structures.Elsevier Applied Science Publisher,London,pp.390-410.

Hung,C.F.;Hwangfu,J.J.(2010):Experimental study of the behaviour of mini-charge underwater explosion bubbles near different boundaries.Journal of Fluid Mechanics,vol.651,pp.55-80.

Hung,C.F.;Hwangfu,J.J.(2008):The experimental studies on the behaviors of bubble near different boundaries subjected to mini-charge underwater explosions.Journal of Taiwan Society of Naval Architects ＆Marine Engineers,vol.27,no.2,pp.59-70.

Klaseboer,E.;Hung,K.C.;Wang,C.W.;Khoo,B.C.(2005):Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure.Journal of Fluid Mechanics,vol.53,no.7,pp.387-413.

Klaseboer,E.;Khoo,B.C.;Hung,K.C.(2005):Dynamics of an oscillating bubble near a floating structure.Journal of Fluids and Structures,vol.21,no.4,pp.395-412.

Koo,W.C.;Kim M.H.(2004):Freely floating-body simulation by a 2D fully nonlinear numerical wave tank.Ocean Engineering,vol.31,no.16,pp.2011-2046.

Lee,T.C.;Keh,H.J.(2013):Thermocapillary motion of a spherical drop in a spherical cavity.Computer Modeling in Engineering ＆Sciences,vol.93,no.5,pp.317-333.

Li,S.;Zhang,A.M.;Wang S.;Han,R.(2018):Transient interaction between a particle and an attached bubble with an application to cavitation in silt-laden flow.Physics of Fluids,vol.30,pp.082111.

Liu,Y.L.;Wang,Q.X.;Wang,S.P.;Zhang,A.M.(2016):The motion of a 3D toroidal bubble and its interaction with a free surface near an inclined boundary.Physics of Fluids,vol.28,no.12,122101.

Liu,Y.L.;Wang,S.P.;Zhang,A.M.(2016):Interaction between bubble and air-backed plate with circular hole.Physics of Fluids,vol.28,no.6,pp.1195-1212.

Liu,Y.L.;Zhang,A.M.;Tian,Z.L.(2014):Approximation of underwater explosion bubble by singularities based on BEM.Ocean Engineering,vol.75,pp.46-52.

Lu,C.H.;He,Y.S.;Wu,G.X.(2000):Coupled analysis of nonlinear interaction between fluid and structure during impact.Journal of Fluids ＆Structures,vol.14,no.1,pp.127-146.

Lundgren,T.S.;Mansour,N.N.(1991):Vortex ring bubbles.Journal of Fluid Mechanics,vol.72,177-196.

Méhauté,B.L.;Wang,S.(1996):Water Waves Generated by Underwater Explosion.World Scientific Publishing World Scientific,River Edge,N.J.

Rungsiyaphornrat,S.;Klaseboer,E.;Khoo,B.C.;Yeo,K.S.(2003):The merging of two gaseous bubble with an application to underwater explosions.Computers ＆Fluids,vol.32,pp.1049-1074.

Stettler,J.W.(1995):Damping Mechanisms and Their Effects on the Whipping Response of a Submerged Submarine Subjected to an Underwater Explosion.Massachusetts Institute of Technology,USA.

Tanizawa,K.(1995):A nonlinear simulation method of 3-D body motions in waves.Journal of the Society of Naval Architects of Japan,vol.178,pp.235-239.

Torsvik,T.;Paris,R.;Didenkulova,I.;Pelinovsky,E.;Belousov,A.et al.(2010):Numerical simulation of a tsunami event during the 1996 volcanic eruption in Karymskoye lake,Kamchatka,Russia.Natural Hazards and Earth System Sciences,vol.10,pp.2359-2369.

Vernon,T.A.(1986):Whipping response of ship hulls from underwater explosion bubble loading.Technical Memorandum 86/255,Defence Research Establishment Atlantic,pp.1-41.

Wang,C.;Khoo,B.C.(2004):An indirect boundary element method for three-dimensional explosion bubbles.Journal of Computational Physics,vol.19,no.4,pp.451-480.

Wang,C.;Khoo,B.C.;Yeo,K.S.(2003):Elastic mesh technique for 3D BIM simulation with an application to underwater explosion bubbles.Computers ＆Fluids,vol.32,no.9,pp.1195-1212.

Wang,H.;Zhu,X.;Cheng,Y.S.;Liu,J.(2014):Experimental and numerical investigation of ship structure subjected to close-in underwater shock wave and following gas bubble pulse.Marine Structures,vol.39,pp.90-117.

Wang,Q.X.(2013):Non-spherical bubble dynamics of underwater explosions in a compressible fluid.Physics of Fluids,vol.25,no.7,pp.131-144.

Wang,Q.X.(2004):Numerical simulation of violent bubble motion.Physics of Fluids,vol.16,no.5,pp.1610-1619.

Wang,Q.X.(2005):Unstructured MEL modeling of nonlinear unsteady ship waves.Journal of Computational Physics,vol.210,pp.368-385.

Wang,Q.X.;Blake,J.R.(2010):Non-spherical bubble dynamics in a compressible liquid.Part 1.Travelling acoustic wave.Journal of Fluid Mechanics,vol.659,pp.191-224.

Wang,Q.X.;Yeo,K.S.;Khoo,B.C.;Lam,K.Y.(1996a):Strong interaction between a buoyancy bubble and a free surface.Theoretical and Computational Fluid Dynamics,vol.8,pp.73-88.

Wang,Q.X.;Yeo,K.S.;Khoo,B.C.;Lam,K.Y.(1996b):Nonlinear interaction between gas bubble and free surface.Computer ＆Fluids,vol.25,no.7,pp.607-628.

Wang,Q.X.;Yeo,K.S.;Khoo,B.C.;Lam,K.Y.(2005):Vortex ring modelling of toroidal bubbles.Theoretical and Computational Fluid Dynamics,vol.19,pp.303-317.

Wang,S.P.;Chu,W.H.;Zhang,A.M.(2014):Experimental study on bubble pulse features under the combined action of horizontal and vertical walls.China Ocean Engineering,vol.28,no.3,pp.293-301.

Wilkerson,S.A.(1985):Elastic Whipping Response of Ships to an Underwater ExplosionLoading.George Washington University,USA.

Wu,G.X.;Hu,Z.Z.(2004):Simulation of non-linear interactions between waves and floating bodies through a finite-element-based numerical tank.Proceedings of the Royal Society A,pp.2797-2817.

Zhang,A.M.;Liu,Y.L.(2015):Improved three-dimensional bubble dynamics model based on boundary element method.Journal of Computational Physics,vol.294,pp.208-223.

Zhang,A.M.;Wu,W.B.;Liu,Y.L.;Wang,Q.X.(2017):Nonlinear interaction between underwater explosion bubble and structure based on fully coupled model.Physics of Fluids,vol.29,no.8,082111.

Zhang,N.;Zong,Z.(2011):The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble.Journal of Fluids ＆Structures,vol.27,no.8,pp.1326-1336.

Zhang,Y.L.;Yeo,K.S.;Khoo,B.C.;Wang,C.(2001):3D jet impact and toroidal bubbles.Journal of Computational Physics,vol.16,no.6,pp.336-360.