Improved Particle Swarm Optimization for Selection of Shield Tunneling Parameter Values

Gongyu Hou,Zhedong Xu, ,Xin Liu and Cong Jin

Abstract: This article proposes an exponential adjustment inertia weight immune particle swarm optimization (EAIW-IPSO) to enhance the accuracy and reliability regarding the selection of shield tunneling parameter values.According to the iteration changes and the range of inertia weight in particle swarm optimization algorithm (PSO),the inertia weight is adjusted by the form of exponential function.Meanwhile,the self-regulation mechanism of the immune system is combined with the PSO.12 benchmark functions and the realistic cases of shield tunneling parameter value selection are utilized to demonstrate the feasibility and accuracy of the proposed EAIW-IPSO algorithm.Comparison with other improved PSO indicates that EAIW-IPSO has better performance to solve unimodal and multimodal optimization problems.When solving the selection of shield tunneling parameter values,EAIW-IPSO can provide more accurate and reliable references for the realistic engineering.

Keywords:Inertia weight,EAIW-IPSO,self-regulation mechanism,shield tunneling parameter.

1 Introduction

Shield tunneling method is widely used in the construction of urban subway tunnels due to its small disturbance to the surrounding environment and low construction cost.Shield tunnel construction is located in the underground space,and the main engineering part relies on the shield machine for construction.Therefore,the control of the ground settlement has a great influence on the shield tunneling.Effective control of ground settlement can ensure smooth construction and requirements of the period.Ground settlement is affected by many factors,including three major categories:factors that cannot be changed (hydrology,geology),factors that are less controllable after the scheme is determined (tunnel radius,shape),and controllable factors [Preisig,Dematteis,Torri et al.(2014)].Among the controllable factors,the selection of shield tunneling parameters is the key to control ground settlement [Bouayad,Emeriault and Maza (2015)].Selecting better shield tunneling parameter values can reduce the interference of construction on the land,control ground settlement value effectively and improve construction efficiency.

Many researchers [Moeinossadat,Ahangari and Shahriar (2017);Zhou,Ding and He (2013)] have studied the selection of shield tunneling parameter values for construction.From the perspective of preventing pressure imbalance in the excavation face,Cao et al.[Cao,Shao and An (2015)] used the least squares support vector machine to construct the nonlinear relationship model between the earth pressure and the tunneling parameters first.The model training is based on the field data samples,and then PSO is applied to optimize the tunneling parameters.On the basis of ensuring the stability of the excavation surface,Li et al.[Li,Fu and Guo (2017)] carried out the orthogonal experiment of the tunneling parameters to improve the tunneling efficiency.The mathematical model between the tunneling speed and the tunneling parameters is constructed and simplified.Then,the tunneling parameters are optimized based on mathematical model.Yang et al.[Yang,Tan and Peng (2017)] studied the shield tunneling parameters in water-soaked round gravel strata.Comparison with tunneling parameters in the complex strata found that the changes of shield tunneling parameter values are small during the construction,except earth pressure.As the same times,the method calculating the value range of the earth pressure is given.Ding et al.[Ding,Wu and Zhang (2015)] use dynamic Bayesian network to optimize the tunneling parameters.First,the dynamic Bayesian network is trained based on data samples from the realistic engineering,obtaining a complete DBN optimization model.Then,the optimal ranges of the tunneling parameters are reversed based on the optimization model,and the real-time tunneling parameter optimization is performed within the optimal range.

With the improvement of the quality requirement in engineering construction,there are more and more factors to be considered when solving realistic engineering problems.The traditional methods to select parameter values will be difficult to implement.Moreover,when using the intelligent optimization algorithms for parameter value selection,the requirement for algorithm performance is also higher.Hence,from the perspective of controlling ground settlement,the article enhances the optimization accuracy and reliability of shield tunneling parameters by improving the performance of optimization algorithm.

Intelligent optimization algorithms include ant colony algorithm [Kiran,Hakli and Gunduz (2015)],genetic algorithm [Bierwirth and Mattfeld (2014)],annealing algorithm [Kulturel-Konak and Konak (2015)],fish swarm algorithm [Yazdani,Sepasmoghaddam,Dehban et al.(2016)],PSO [Khan,Kamran,Rehman et al.(2017)] and others.PSO is widely used in many engineering fields [Goel,Gupta and Panchal.(2012);Kuo and Yang (2011);Liu,Cai and Wang (2010);Seyedpoor,Salajegheh and Salajegheh (2012)] due to its fast convergence speed and high efficiency.Meanwhile,PSO also has some deficiency.It converges faster in the early iterations,slows down in the later iterations,and is easy to fall into local optima.The global search ability can continue to be improved.A number of researchers have made some improvements to its performance by adjusting the inertia weight dynamically.Shi et al.[Shi and Eberhart (1998)] developed that the inertia weight should be linearly decremented during the iterative process and range from 0.9 to 0.4.As for this adjustment strategy,if the better position is not searched in the early iterations,it will easily fall into the local optima due to the reduction of the inertia weight.Therefore,the optimization accuracy based on this adjustment strategy is still not high.Zhang et al.[Zhang,Yu and Hu (2003)] proposed a way to randomly change the inertia weight.The value of the inertia weight may be big in the late iterations based on random change strategy.However,the big inertia weight makes the algorithm have a strong global search capability,which may destroy the search of the global optimal value for multimodal functions and obtain the local optimum in the end.Han et al.[Han,Li,and Wei (2006)] adjusted the inertia weight according to the fitness value of each particle and the premature condition of the particle group.However,the local optima will have a greater impact on the adjustment of other particles under this adjustment strategy.It will be easy to fall into local optima for multimodal function.Feng et al.[Feng and Liu (2016)] adopted PSO with exponentially decreasing inertia weight to solve non-differentiable NPhard problem of absolute value equations.Adjusting the inertia weight in exponentially decreasing form improves the convergence speed to some extent,but the particle diversity in the later iterations cannot be guaranteed and algorithm still cannot obtain a better global optimal value.

Studies find that the improved PSO algorithms based on dynamic adjustment inertia weight from former researchers are also easy to fall into the local optima.The global search ability is still insufficient.In addition,particles adjust themselves according to the surrounding particle positions.The dependence between the particles is large and the particle group lacks the adjustment mechanism,which is also one reason why PSO is easy to fall into the local optima.In order to enhance the accuracy and reliability regarding the selection of shield tunneling parameter values based on PSO,the new adjustment equation of the inertia weight is given first.Meanwhile,the self-regulation mechanism of the immune system is combined with PSO.12 benchmark functions are applied to test the performance of EAIW-IPSO.Then,EAIW-IPSO is applied to solve the selection of shield tunneling parameter values.The realistic cases of shield tunneling parameter optimization are studied at the end.

The rest of the paper is organized as follows:The second section gives basic PSO theory and improvement analysis.The third section specifically improves PSO and proposes EAIW-IPSO.The fourth section proves the performance of EAIW-IPSO based on 12 benchmark functions.The fifth section constructs the optimization method of the tunneling parameters based on EAIW-IPSO.Realistic cases for shield tunneling parameter optimization are studied in the sixth section.Conclusions are presented in seventh section.

2 The basic PSO theory and improvement analysis

PSO is one of the computational intelligence methods,which is a process of simulating bird foraging [Sedghizadeh and Beheshti (2018)].Each bird is assumed as a particle in PSO.Particle velocity and position are updated by two optimal positions [Chen,Li,Xiao et al.(2018)].One of the optimal positions is the personal best position and the other optimal position is the global best position.Particles are extended toN-dimensional space.The size of particle group isM.The position of particleiis expressed as vectorXi=(xi1,xi2,…,xiN) and velocity is expressed as vectorVi=(vi1,vi2,…,viN).The velocity and position update according to the Eqs.(1) and (2) [Nie,Wang,Xiao et al.(2017)].

whereωis inertia weight,c1andc2are acceleration constants,r1andr2are random values within the range of (0,1),pisis personal best position of theith particle insth direction (i＝1,2,…,M) (s＝1,2,…,N),pgsis global best position insth direction.

Many researchers have studied the inertia weight in Eq.(1) [Chatterjee and Siarry (2006);Miao,Shi,Zhang et al.(2009);Pluhacek,Senkerik,Davendra et al.(2013);Taherkhani and Safabakhsh (2016);Uma,Gandhi and Kirubakaran (2012)].Inertia weight is initially seen as a constant value,but subsequent studies have found that changing the inertia weight value has an impact on algorithm performance.The adjustment equation for inertia weight that was first adopted is as follows:

whereωminis minimum value of inertia weight,ωmaxis maximum value of inertia weight,tis current number of iterations,Tis maximum number of iterations.

In Eq.(3),the inertia weight is linearly decremented during the iterative process.With the deepening of the research,however,researchers have analyzed and concluded that the change of inertia weight should be a nonlinear adjustment in the iterative process.Eq.(4) applies random function to adjust the inertia weight nonlinearly.

Eq.(5) and Eq.(6) use the exponential form to dynamically adjust the inertia weight,which is also a typical nonlinear adjustment strategy.

whered1,d2are control constants.

According to the curve of exponential decreasing function,it can be found that the curve of exponential decreasing function is consistent with the iterative process of PSO.Therefore,the form of exponential decreasing is selected to adjust the inertia weight first.Meanwhile,this article considers the range of inertia weight and the change of inertia weight in the iterative process.

In addition,particles adjust themselves according to the surrounding particle positions and lack the mechanism of variation,which may lead to poor particle diversity [Chen,Cao,Ye et al.(2013)].In order to solve such problems,the self-regulation mechanism of the immune system will be used to select the next generation of group.

3 EAIW-IPSO

According to the range of inertia weight value,first,the initial exponential form to adjust the inertia weight is constructed as follows.

In Eq.(7),when random number is 0,ωisωmin.ωwill beωmaxwhen random number is 1.In addition,the study results show that the global search ability is strengthened when the inertia weight is big and the local search ability is strong when the inertia weight is small.The inertia weight should be dynamically adjusted during the iterative process.In the early stage to search for the global optimal value in a large range,the global search ability should be strengthened.At this time,the inertia weight should be big.The inertia weight should be reduced in the late iterations,and the optimal value search should be performed in the local range.Therefore,the inertia weight should be reduced as the number of iterations increases.In order to improve the speed of convergence to the vicinity of the global optimal value in the early iterations,and then perform local search near the optimal value,Eq.(7) is modified as follows according to the above analysis:

In Eq.(8),the value oftis small in early stage,the value of (1-(t/T)2) will be big.Due to the value of (ωmax/ωmin) is over 1,ωwill be big according to the monotonicity of exponential function.In the late iterations,the value of (1-(t/T)2) will decrease with the increase oft,so thatωwill decrease.

Moreover,to further reduce the possibility of falling into local optima in the search process,the article selects the next generation group based on the self-regulation mechanism of the immune system.The specific selection strategy is:before the end of the each iteration,another particle group with size ofMis initialized and the fitness value of the corresponding particle is calculated.Updated and initialized particles form a group with size of 2M.Then,Mparticles with relatively large fitness value in particle group with size of 2Mare selected as the next generation particle group.

The steps and procedures of the EAIW-IPSO are realized as follows:

Step1:Set the size of particle groupM,maximum number of iterationsT,acceleration constantsc1andc2,minimum and maximum values of inertia weightωminandωmax.

Step2:Initialize the position and velocity values for all particles in group,calculate the fitness value of each particle,set the global best positionPg=(pg1,pg2,…,pgq) and the personal best positionPi=(pi1,pi2,…,piq) (i＝1,2,…,M).

Step3:Update the position and velocity values based on Eqs.(1),(2) and (8),calculate the fitness value of each updated particle,update the global best positionPgand the personal best positionPi(i＝1,2,…,M).

Step4:Initialize another particle group with size ofM,calculate fitness value and set the personal best positionPi(i＝1,2,…,M) for initialized particles.

Step5:Sort the fitness values about 2Mparticles in updated and initialized group,select theMparticles with relatively large fitness value as next iteration group.

Step6:If the termination condition is satisfied,the iterations stop.Otherwise,the next iteration is entered.

4 Experimental study

12 benchmark functions in Tab.1 are applied to test the performance of the proposed EAIW-IPSO algorithm.f1,f2,f3,f7,f8,f9are unimodal with only one optimum and the others are multimodal with some local optima.All functions obtain the standard optimal value of 0.Meanwhile,EAIW-IPSO has also been tested against with PSO,linear decreasing inertia weight particle swarm optimization (LDIW-PSO),random inertia weight particle swarm optimization (RIW-PSO),and exponentially decreasing inertia weight particle swarm optimization (EDIW-PSO).

Experiment parameters are set as follows:the minimum and maximum values of inertia weight are 0.4 and 0.9,the maximum number of iterations is 100,the acceleration constantsc1andc2are 2,and the size of particle group is 50.

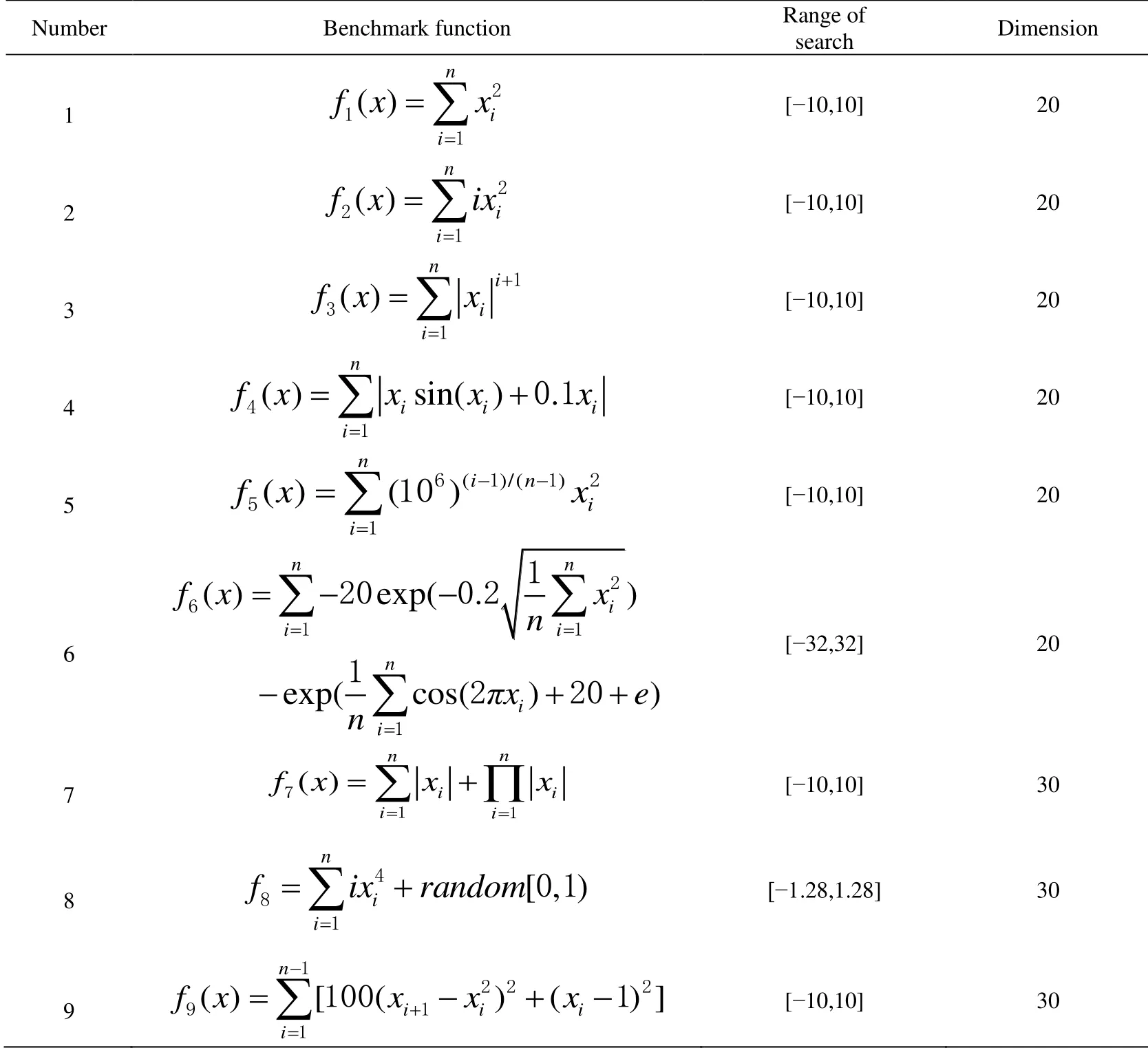
Table 1:12 benchmark functions

Number Benchmark function Range of search Dimension 10 ( ) / cos( / )n n i i i=1 i=1 f x x x i+-∑ ∏2 10=1 4000 1 [-200,200] 30 11 ( ) .sin( )i i i f x n x x n- =1= × -∑1 11 418 9829 [-500,500] 30 12 ( ) [ cos( ) ]n i i i=1 f x x πx= - +∑ 2 12 10 2 10 [-5.12,5.12] 30

The five algorithms run 20 times independently in each function.The indicators to evaluate the performance of the algorithm are:the best value of 20 run,the mean value,and the root mean square error (RMSE).Among these indicators,the best and mean values are used to evaluate the optimization accuracy of the algorithm,and RMSE is to evaluate the optimization stability.The simulation results are shown in Tab.2.Meanwhile,all best and mean values have been drawn as line charts.

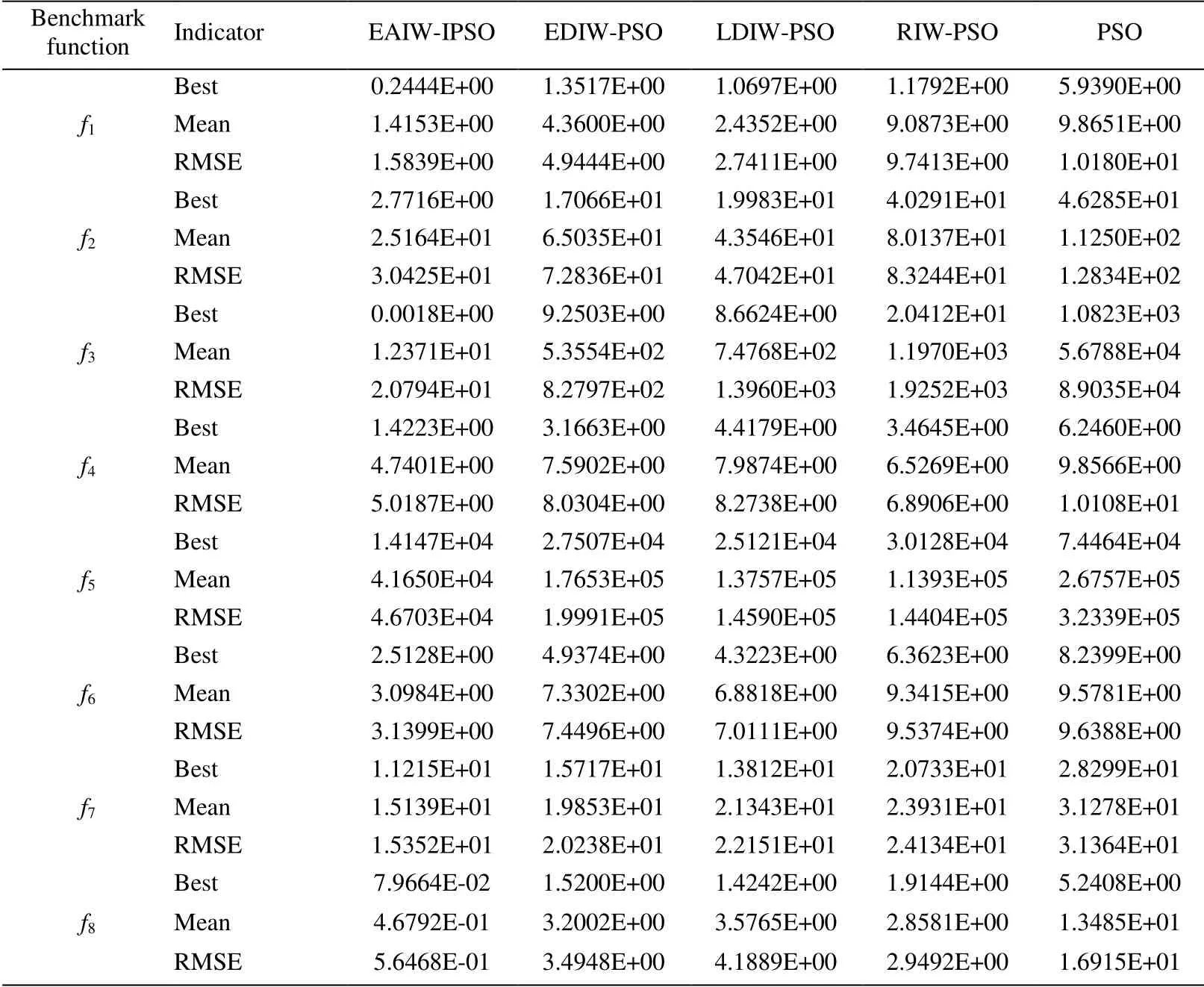
Table 2:Simulation results of 12 benchmark functions

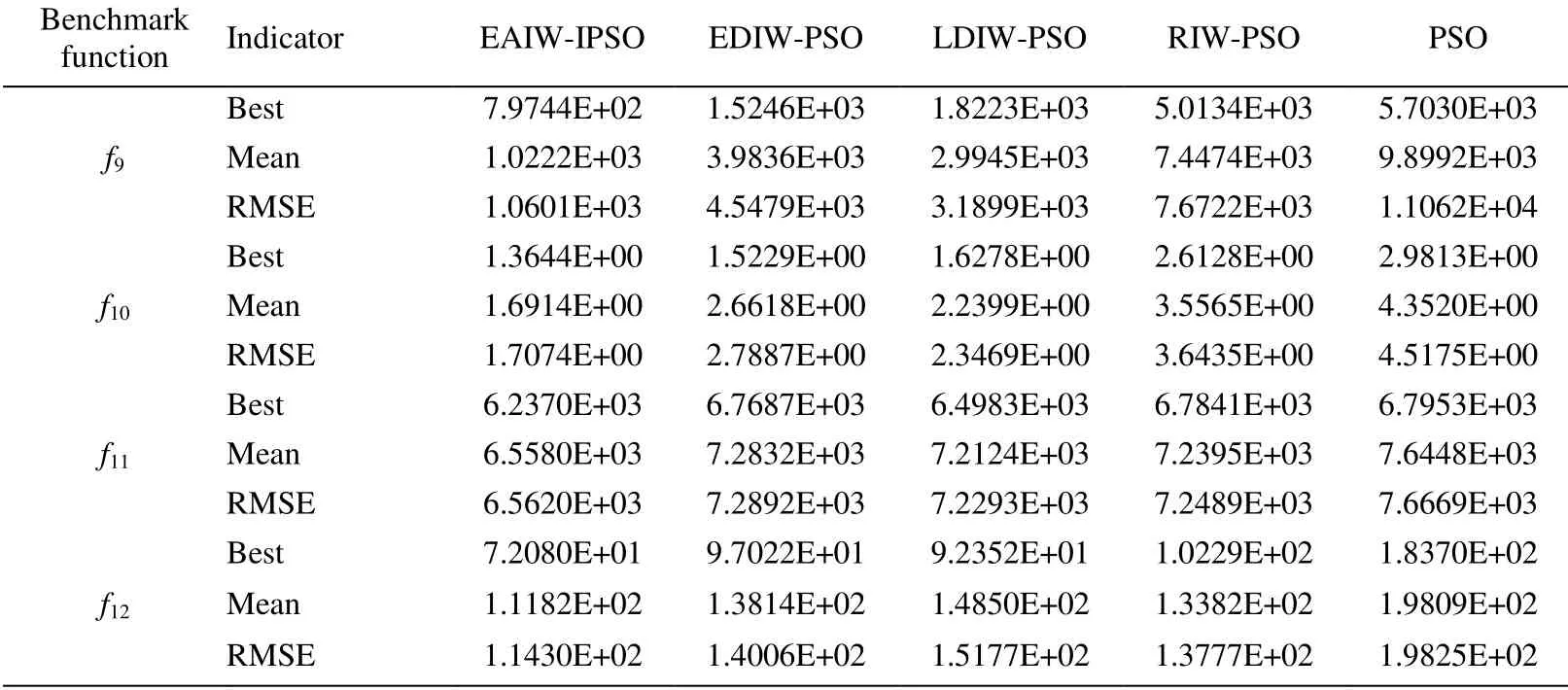
Benchmark function Indicator EAIW-IPSO EDIW-PSO LDIW-PSO RIW-PSO PSO f9 Best 7.9744E+02 1.5246E+03 1.8223E+03 5.0134E+03 5.7030E+03 Mean 1.0222E+03 3.9836E+03 2.9945E+03 7.4474E+03 9.8992E+03 RMSE 1.0601E+03 4.5479E+03 3.1899E+03 7.6722E+03 1.1062E+04 f10 Best 1.3644E+00 1.5229E+00 1.6278E+00 2.6128E+00 2.9813E+00 Mean 1.6914E+00 2.6618E+00 2.2399E+00 3.5565E+00 4.3520E+00 RMSE 1.7074E+00 2.7887E+00 2.3469E+00 3.6435E+00 4.5175E+00 f11 Best 6.2370E+03 6.7687E+03 6.4983E+03 6.7841E+03 6.7953E+03 Mean 6.5580E+03 7.2832E+03 7.2124E+03 7.2395E+03 7.6448E+03 RMSE 6.5620E+03 7.2892E+03 7.2293E+03 7.2489E+03 7.6669E+03 f12 Best 7.2080E+01 9.7022E+01 9.2352E+01 1.0229E+02 1.8370E+02 Mean 1.1182E+02 1.3814E+02 1.4850E+02 1.3382E+02 1.9809E+02 RMSE 1.1430E+02 1.4006E+02 1.5177E+02 1.3777E+02 1.9825E+02

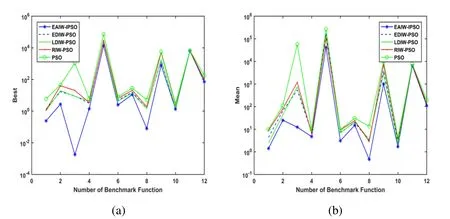
Figure 1:Simulation results (a) Best,(b) Mean

4.1 Unimodal function

The optimization performance of the five algorithms in unimodal function can be analyzed according to the simulation results off1,f2,f3,f7,f8,f9.As shown in Tab.2,the best and mean values of PSO are all the biggest in five algorithms.The best and mean values of LDIW-PSO,EDIW-PSO,and RIW-PSO are smaller than PSO respectively,but these algorithms cannot solve these unimodal functions all with good accuracy.EAIWIPSO obtains the best solutions among these algorithms.In addition,it also can be seen from Fig.1,the lines of best and mean corresponding to EAIW-IPSO are all the lowest,which shows that EAIW-IPSO obtains more accurate optimization values inf1,f2,f3,f7,f8,f9.Meanwhile,RMSE values verify the stability of EAIW-IPSO.Therefore,EAIW-IPSO can obtain a more stable and accurate solution compared with other four algorithms in unimodal functions.The optimization processes off1,f2,f3,f7,f8,f9are shown in Fig.2.

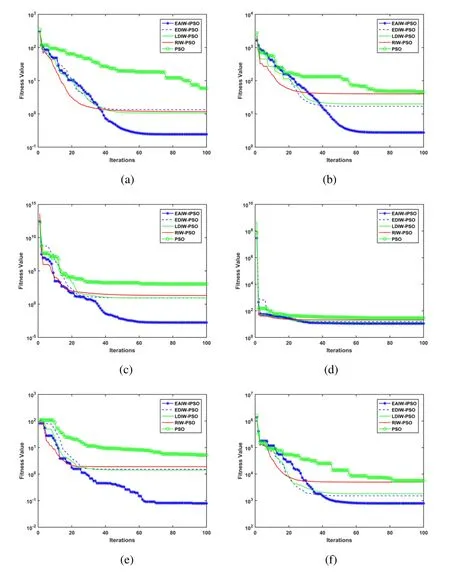
Figure 2:Unimodal functions (a) f1,(b) f2,(c) f3,(d) f7,(e) f8,(f) f9

In Fig.2,the graphical results show the changing curve of the fitness value with the iterations of different algorithms forf1,f2,f3,f7,f8,f9.As shown in Fig.2,LDIW-PSO,EDIW-PSO,and RIW-PSO have a faster convergence rate,but their global search values at the early stage are worse than the value of EAIW-IPSO.Compared with other algorithms,EAIW-IPSO can quickly converge to a more accurate value,and then converge to a better solution with the local search in the late iterations.Therefore,the convergence characteristics show that EAIW-IPSO has a stronger search capability and can obtain more accurate global optimal value for unimodal functions.

4.2 Multimodal function

The functions off4,f5,f6,f10,f11,f12are multimodal with some local optima.It can be seen from Tab.2 that the optimization values obtained from LDIW-PSO,EDIW-PSO,and RIW-PSO are close,which shows that these three algorithms have the relatively close level in accuracy for multimodal functions.According to the positions corresponding to multimodal functions in lines of best and mean in Fig.1,EAIW-IPSO does not show particularly good accuracy inf11.But the optimization values of EAIW-IPSO are much better in other multimodal functions.The stability of EAIW-IPSO is also better than that of other algorithms.Therefore,EAIW-IPSO still has high accuracy in multimodal functions.The iteration processes off4,f5,f6,f10,f11,f12are shown in Fig.3.

The graphical results show the changing curve of the fitness value with the iterations of different algorithms forf4,f5,f6,f10,f11,f12.As can be seen,EAIW-IPSO can converge to a more accurate value quickly at the early stage too.The search ability is still strong to obtain a better global optimal value in the late iterations,which shows that EAIW-IPSO has better performance to overcome the problem of falling into the local optima.

According to the performance analysis of five algorithms in unimodal and multimodal functions,EAIW-IPSO has better accuracy and convergence characteristics.EAIW-IPSO integrates the advantage of maintaining the particle diversity through self-regulation mechanisms in immune algorithm.Therefore,the iteration process allows for a wider range of search,reduces the influence of local optimal particle position on other particles and has better ability to gain global optimal value.Moreover,EAIW-IPSO has better convergence characteristic of other improved PSO by adjusting inertia weight in exponential form.The PSO that uses the exponential form to adjust the inertia weight can quickly converge to the position of the global optimal value in the early iterations,which can improve the iterative efficiency of the algorithm.

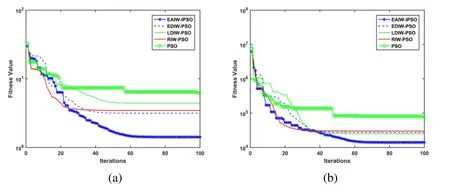
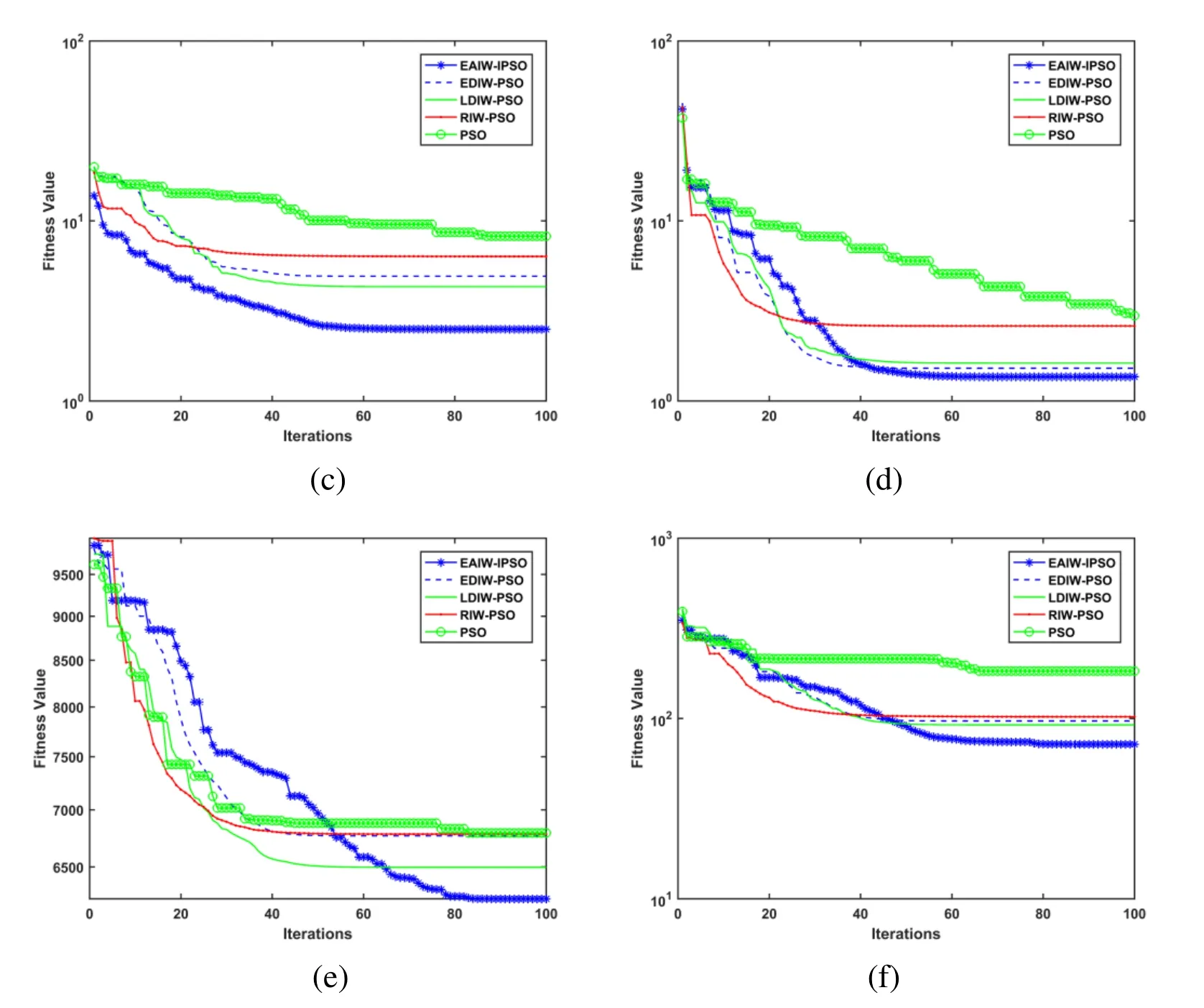
Figure 3:Multimodal functions (a) f4,(b) f5,(c) f6,(d) f10,(e) f11,(f) f12

In summary,the optimization values obtained from EAIW-IPSO are more accurate and stable compared with other four algorithms,regardless of the unimodal or multimodal optimization problems.EAIW-IPSO has better overall performance to search the global optimal value.

5 Shield tunneling parameter optimization based on EAIW-IPSO

Before using EAIW-IPSO to optimize the shield tunneling parameters,it is necessary to construct the relationship model between the tunneling parameters and the ground settlement.To better predict the nonlinear relationship between the tunneling parameters and ground settlement in realistic projects,the article also considers the geometric and formation condition parameters.BP neural network optimized by genetic algorithm (GABP) is applied to construct the nonlinear relationship prediction model between selected engineering parameters and ground settlement.Based on realistic data,the neural network prediction model is trained.The final weights and thresholds of the trained neural network could be obtained.The neural network model to predict the relationship between selected engineering parameters and ground settlement can be constructed as follows:

wherewijis obtained weight between input layer and hidden layer;hjis obtained threshold of hidden layer;wj’ is obtained weight between hidden layer and output layer;his obtained threshold in output layer;Lis number of nodes in hidden layer;kiis theith selected engineering parameter;qis the number of engineering parameters;f(x) is activation function.Then,EAIW-IPSO is adopted to optimize the tunneling parameters under specific geometric and formation conditions based on predictive model.

The following values need to be set:the maximum number of iterationsH,acceleration constantsc1andc2,minimum and maximum values of inertia weightωmin,ωmax,and particle group sizeM.According to the selected engineering parameters,the particle space dimension isq.The selected engineering parameters need to be initialized as the position of particleXi＝ (xi1,xi2,…,xiq) ＝(k1i,k2i,…,kqi) (i＝1,2,…,M).In addition,the late change values of the selected engineering parameters need to be initialized as the particle velocityVi＝ (vi1,vi2,…,viq) (i＝1,2,…,M).The important thing to note is that the geometric and formation condition parameter values should be constant during the optimization process.

Each particle fitness value is calculated based on the obtained predictive model.The fitness value of particleI(I＝1,2,…,M) is:

The initialized position for each particle is taken as the corresponding personal best positionPi＝(pi1,pi2,…,piq) ＝(xi1,xi2,…,xiq) (i＝1,2,…,M).The position ofgth particle with maximum fitness value are considered as global best positionPg＝(pg1,pg2,…,pgq) ＝(xg1,xg2,…,xgq).Particle velocity and position are updated by Eqs.(1) and (2).Meanwhile,Eq.(8) is adopted to calculate inertia weight.Then,the updated particle fitness values are calculated again.The personal best position of each particle and global best position are updated.

OtherMparticles are initialized and corresponding fitness value is calculated too.The personal best position of each initialized particle is set.And then,all particle fitness values in updated and initialized groups are sorted.TheMparticles with relatively large fitness value are selected as the next iteration group.Meanwhile,the personal best position of particle and global best position are updated.Cycling iteration process until the number of iterations is over.

6 Case study for shield tunneling parameter optimization

6.1 Case 1

Shield tunneling parameter optimization of Changsha metro line 1 is selected as the study case.The tunneling parameters that affect the ground settlement considered in this case are:synchronous grouting amount,shield thrust,cutter head torque,the ratio of tunneling speed and cutter speedR(the cutter speed is usually 1.5 rad/min),and earth pressure.As the same time,geometric condition parameter is:the ratio of buried depthHand diameter excavationD.Formation condition parameters are:groundwater level,cohesion,internal friction angle,earthwork heavy,and side-pressure coefficient.Since the main objective of the study is to find the best tunneling parameter values to minimize the ground settlement,the 34 groups of samples [Mou (2013)] with small ground settlement values are applied to train and test predictive model of neural network (the number of training samples is 30 and other 4 groups of samples are used to test predictive performance).Tab.3 shows all sample data.The samples are normalized in [-1,1] [Tran and Hoang (2016)].The training performance of predictive model is shown in Fig.4.Tab.4 shows the test results.

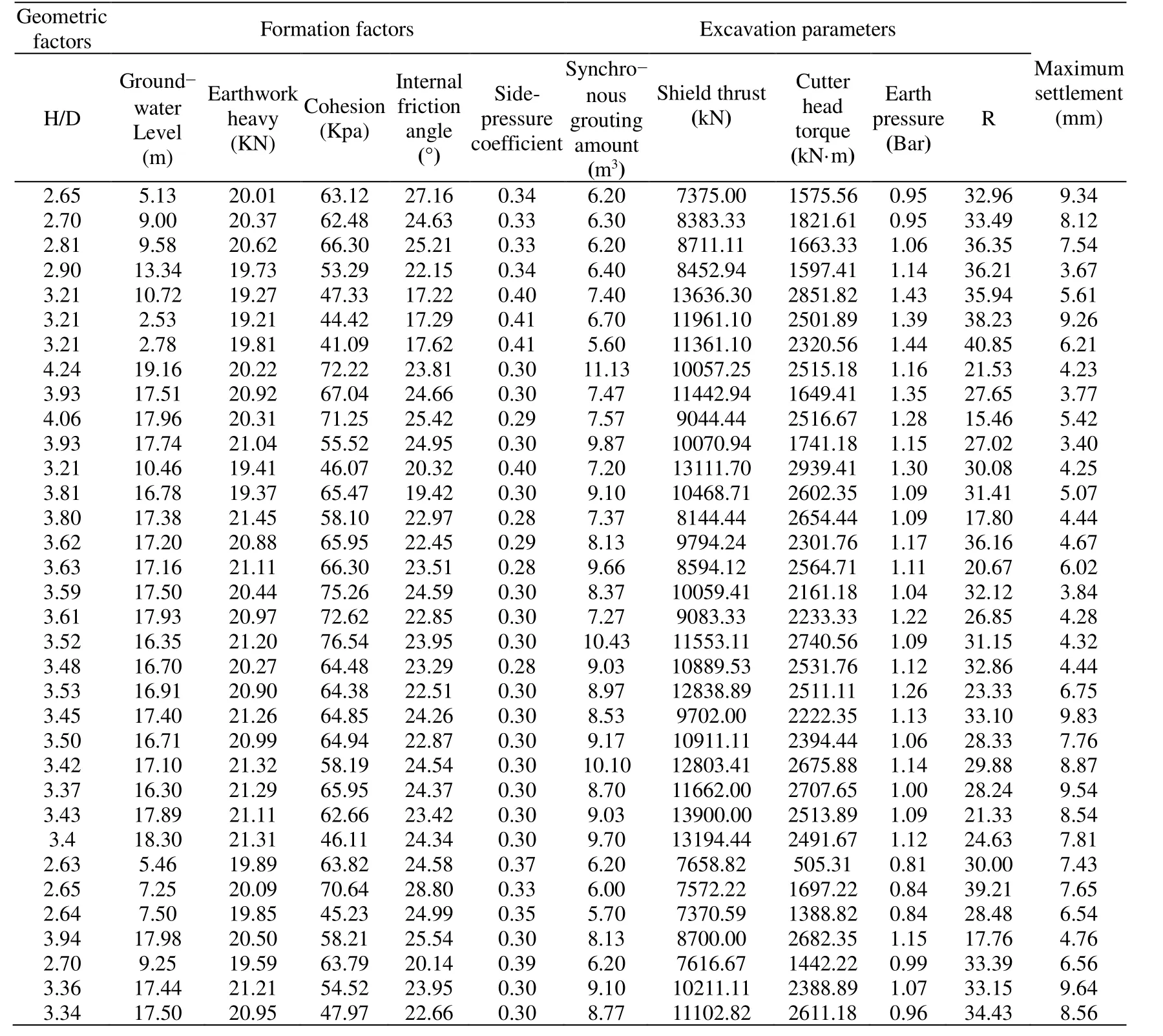
Table 3:Sample data in case 1

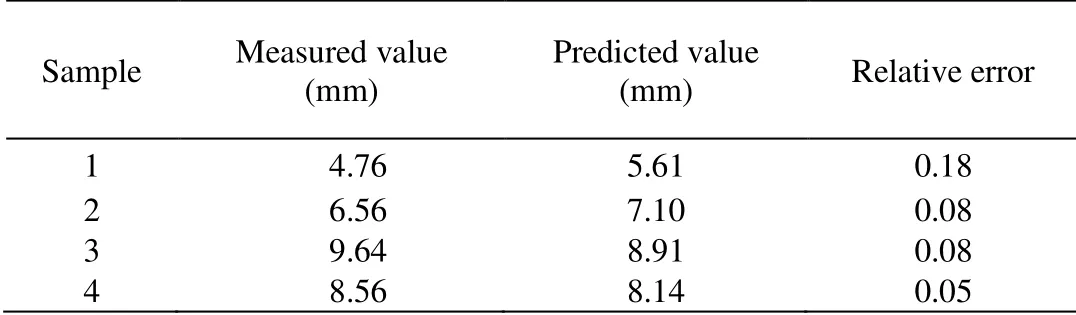
Table 4:Test results for 4 groups of test samples in case 1

It can be seen,the relative errors are all controlled within 0.15,except first test sample.The mean of relative errors is 0.10.As for the realistic engineering application,the test results are better.Based on the obtained predictive model,PSO,LDIW-PSO,RIW-PSO,EDIW-PSO,and EAIW-IPSO are respectively conducted to optimize the tunneling parameters in tunnel section that geometric and formation condition parameter values are shown in Tab.5.The obtained ground settlement values are shown in Tab.6.

Figure 4:Training performance of the predictive model in case 1

Table 5:Geometric and formation condition parameter values in case 1

The results in Tab.6 show that the ground settlement values based on EAIW-IPSO is the smallest,which also illustrate the better performance of EAIW-IPSO compared with other improved PSO algorithms.Because there are many other influencing factors at the construction site and the error of predictive model,the realistic and optimized ground settlement values will be different when using the optimized tunneling parameter values for construction.Meanwhile,the existence of other influencing factors and the error of predictive model make the optimized tunneling parameter values different from the optimal values at the construction site.Hence,the final adopted tunneling parameter values in realistic engineering need to be further adjusted according to the optimized values.Tab.7 shows the optimized tunneling parameter values based on EAIW-IPSO and adjusted tunneling parameter values.

Table 6:Optimization results of 5 algorithms in case 1

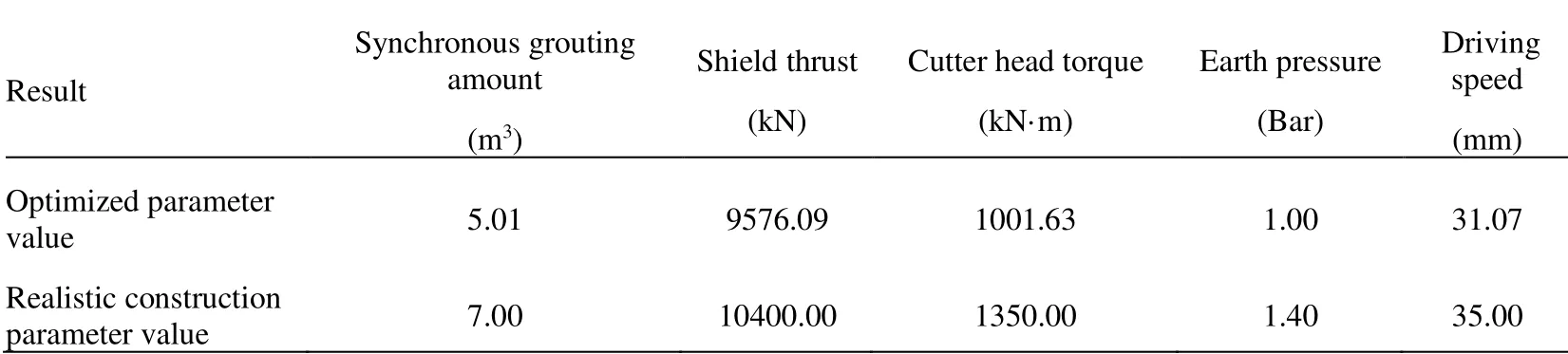
Table 7:The optimized and adjusted tunneling parameter values in case 1

As can be seen from Tab.7,the obtained parameter values based on EAIW-IPSO are close to the final adopted tunneling parameter values,which illustrate that the tunneling parameter values obtained from EAIW-IPSO can provide better references for selection of realistic tunneling parameter values.Hence,EAIW-IPSO can avoid blindness in selecting parameter values in engineering.

6.2 Case 2

Changsha-Zhuzhou-Xiangtan Intercity Railway is selected as the second case study.The tunneling parameters considered in this case are:synchronous grouting amount,shield thrust,cutter head torque,the ratio of tunneling speed and cutter speedR,earth pressure,and slag amount.Meanwhile,geometric condition parameter is:the ratio of buried depthHand diameter excavationD.Formation condition parameters are:groundwater level and earthwork heavy.The sample data are shown in Tab.8.

Table 8:Sample data in case 2

Geometric factors Formation factors Excavation parameters Maximum settlement (mm) H/D Groundwater Level (m) Earthwork heavy (KN) Cutter head torque (kN·m) Shield thrust (kN) Earth pressure (Bar) Slag amount (m3) Synchronous grouting amount (m3) R 2.79 19.26 22.60 7760 23076 1.56 191.00 13.17 10.92 13.72 4.26 32.21 21.44 8461 28585 1.85 194.29 18.39 16.31 4.38 3.49 23.61 22.16 8022 25696 1.54 191.44 13.17 10.26 13.61 3.41 22.77 22.07 8292 22471 1.31 193.00 13.17 11.99 9.35 3.37 21.49 22.38 5694 23942 1.39 191.78 13.17 12.30 7.28 3.26 21.37 22.63 7508 26043 1.45 191.33 18.62 12.61 2.93 3.15 21.53 22.64 8343 25687 1.64 192.56 18.42 12.20 14.52 3.21 20.96 22.07 7186 25332 1.45 192.25 18.40 13.20 10.24 3.22 21.36 21.90 7957 25876 1.55 191.78 18.48 13.40 7.00 3.33 22.31 22.71 9009 29399 1.54 192.25 18.54 12.48 10.66 3.39 22.49 22.89 8576 28542 1.74 192.13 18.46 13.77 8.90 3.46 27.69 21.88 7436 28279 1.53 192.43 18.50 12.34 12.33 3.95 29.3 21.88 9169 27617 1.58 192.38 18.38 13.67 7.17 4.03 30.43 23.26 5752 30341 1.87 194.13 21.92 14.86 7.43 4.07 30.33 23.42 6787 28612 2.01 191.13 18.35 16.08 5.63 4.11 29.61 22.98 6419 31046 2.11 194.25 18.41 15.88 7.80 4.15 29.83 22.50 7779 32384 2.32 193.00 18.50 16.75 5.94 4.19 31.00 22.03 8261 29853 2.17 194.75 18.70 16.10 6.12 4.23 31.83 21.69 7576 30325 1.84 192.43 18.67 15.97 8.17 3.55 26.08 22.00 8707 35224 2.08 192.00 18.50 6.95 15.10 4.22 29.58 21.15 9481 42297 2.84 190.88 18.69 3.11 9.87 3.43 21.28 22.04 8005 26086 1.28 191.33 13.17 11.94 0.35 2.48 13.41 20.20 6601 32493 1.64 191.67 13.46 4.00 17.05 2.57 15.25 20.63 6743 27191 1.74 192.33 13.18 7.17 18.61 3.19 23.09 22.48 9016 26899 1.49 191.44 13.17 9.94 15.75 3.25 22.63 21.71 8268 25388 1.67 191.88 18.54 14.05 16.72 3.55 26.08 22.00 8707 35224 2.08 192.00 18.5 6.95 15.10 4.67 31.89 20.96 7667 26703 1.87 192.14 18.38 15.74 4.44 4.71 31.12 20.65 7073 28116 1.89 192.14 18.56 13.75 5.95 4.68 30.35 20.76 7619 36277 2.01 191.86 18.66 13.45 11.44 3.14 21.66 22.43 7530 25918 1.61 192.5 18.30 12.74 10.59 3.99 29.89 22.55 5691 24215 1.58 194.25 18.47 14.91 7.49 3.17 21.48 22.22 7675 25997 1.44 192.57 18.45 12.73 10.19 3.28 22.97 21.99 7351 27787 1.75 191.71 18.50 13.27 15.35 2.74 18.18 21.41 4312 20659 1.16 192.33 13.18 9.54 4.99

Based on sample data,the predictive model in this case is trained.The training performance of predictive model is shown in Fig.5.Tab.9 shows the test results.

As can be seen in Tab.9,the maximum relative error is controlled within 0.15.The mean of relative errors is 0.09.Therefore,the test results are also better for the realistic engineering application.Based on the obtained predictive model,five algorithms are respectively applied to optimize the tunneling parameters in tunnel section that geometric and formation condition parameter values are shown in Tab.10.

Table 9:Test results for 4 groups of test samples in case 2

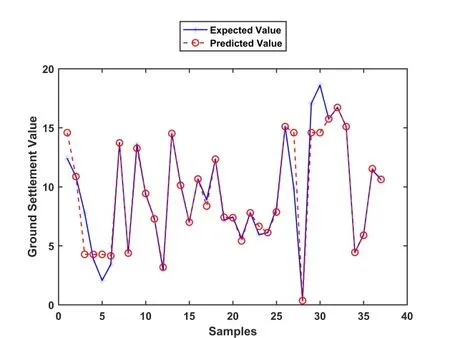
Figure 5:Training performance of the predictive model in case 2

Table 10:Geometric and formation condition parameter values in case 2

The obtained ground settlement values are shown in Tab.11.The results also prove the better performance of EAIW-IPSO.As can be seen in Tab.11,the ground settlement value after optimized is close to 0,which is an ideal value.In realistic engineering,the existence of many influencing factors will lead to the ground settlement.Hence,the optimized tunneling parameter values should be used to test its realistic ground settlement value first.And then,the final adopted tunneling parameter values in realistic engineering are further adjusted according to the optimized values.Tab.12 shows the optimized tunneling parameter values based on EAIW-IPSO and adjusted tunneling parameter values in this case.

Tab.12 also illustrates that the obtained parameter values based on EAIW-IPSO can provide better references for selection of realistic tunneling parameter values.Therefore,tunneling parameters are optimized based on EAIW-IPSO first in realistic projects,and then further adjusted according to the optimized values,which will improve the efficiency of the tunneling parameter value selection.

Table 11:Optimization results of 5 algorithms in case 2

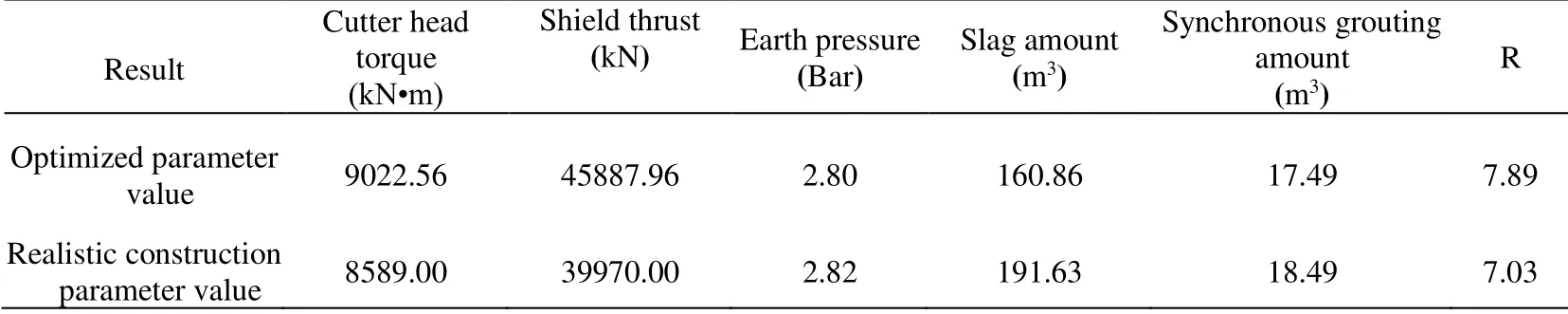
Table 12:The optimized and adjusted tunneling parameter values in case 2

7 Conclusions

The selection of shield tunneling parameter values has a very important influence on tunnel construction.To provide more accurate and reliable references for selection of shield tunneling parameter values based on PSO,the article proposes EAIW-IPSO.In proposed algorithm,the new adjustment equation for inertia weight is given,and selfregulation mechanism of the immune system is combined with the PSO.EAIW-IPSO has been tested against with PSO,LDIW-PSO,RIW-PSO,EDIW-PSO based on 6 unimodal functions and 6 multimodal functions.Simulation results indicate that EAIW-IPSO can converge to a more accurate value at the early stage quickly,and local search ability is still strong in the late iterations.In addition,the proposed algorithm has better performance to overcome the problem of falling into the local optima.

The optimization method of shield tunneling parameters is constructed based on the proposed EAIW-IPSO.GA-BP neural network is applied to construct the predictive model between the selected engineering parameters and ground settlement first.EAIWIPSO is used to optimize tunneling parameters under specific geometric and formation condition based on predictive model.To evaluate the performance of the proposed algorithm in selecting the shield tunneling parameter values,two realistic cases are studied.The case results verify the feasibility and accuracy of EAIW-IPSO.Therefore,EAIW-IPSO can improve the efficiency for the selection of tunneling parameter values in realistic engineering.

Acknowledgments:The authors are grateful for the support provided by the Co-funding of National Natural Science Foundation of China and Shenhua Group Corporation Ltd (Grant No.U1261212) and the Program of Major Achievements Transformation and Industrialization of Beijing Education Commission (Grant No.ZDZH20141141301).

Conflicts of Interest:The authors have no conflicts of interest to declare.

References

Bierwirth,C.;Mattfeld,D.C.(2014):Production scheduling and rescheduling with genetic algorithms.Evolutionary Computation,vol.7,no.1,pp.1-17.

Bouayad,D.;Emeriault,F.;Maza,M.(2015):Assessment of ground surface displacements induced by an earth pressure balance shield tunneling using partial least squares regression.Environmental Earth Sciences,vol.273,no.11,pp.7603-7616.

Cao,X.;Shao,C.;An,Y.(2015):Earth pressure prediction and optimal control intelligent strategy for shield chamber.Journal of China Coal Society,vol.40,no.12,pp.2979-2986.

Chatterjee,A.;Siarry,P.(2006):Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization.Computers ＆Operations Research,vol.33,no.3,pp.859-871.

Chen,Y.;Li,L.;Xiao,J.;Yang,Y.;Liang,J.et al.(2018):Particle swarm optimizer with crossover operation.Engineering Applications of Artificial Intelligence,vol.70,no.2018,pp.159-169.

Chen,Z.J.;Cao,H.Y.;Ye,K.;Zhu,H.P.;Li,S.F.(2013):Improved particle swarm optimization-based form-finding method for suspension bridge installation analysis.Journal of Computing in Civil Engineering,vol.29,no.3,04014047.

Ding,B.J.;Wu,X.G.;Zhang,L.M.;Zhong,J.B.;Liu,Y.(2015):Optimization of shield tunneling parameters based on dynamic Bayesian networks.Chinese Journal of Rock Mechanics and Engineering,vol.34,no.s1,pp.3215-3222.

Feng,J.M.;Liu,S.Y.(2016):Particle swarm optimization algorithm based on inertia weight exponentially decreasing for solving absolute value equations.Journal of Jilin University(Science Edition),vol.54,no.6,pp.1265-1269.

Goel,L.;Gupta,D.;Panchal,V.K.(2012):Hybrid bio-inspired techniques for land cover feature extraction:a remote sensing perspective.Applied Soft Computing Journal,vol.12,no.2,pp.832-849.

Han,J.H.;Li,Z.R.;Wei,Z.C.(2006):Adaptive particle swarm optimization algorithm and simulation.Journal of System Simulation,vol.54,no.6,pp.2969-2971.

Islam,B.;Baharudin,Z.;Nallagownden,P.(2017):Development of chaotically improved meta-heuristics and modified BP neural network-based model for electrical energy demand prediction in smart grid.Neural Computing ＆Applications,vol.28,no.s1,pp.877-891.

Khan,S.;Kamran,M.;Rehman,O.U.;Liu,L.;Yang,S.(2017):A modified PSO algorithm with dynamic parameters for solving complex engineering design problem.International Journal of Computer Mathematics,vol.2017,no.3,pp.1-30.

Kiran,M.H.;Hakli,S.;Gunduz,M.;Uguz,H.(2015):Artificial bee colony algorithm with variable search strategy for continuous optimization.Information Sciences,vol.300,no.2015,pp.140-157.

Kulturel-Konak,S.;Konak,A.(2015):A large-scale hybrid simulated annealing algorithm for cyclic facility layout problems.Engineering Optimization,vol.47,no.7,pp.963-978.

Kuo,R.J.;Yang,C.Y.(2011):Simulation optimization using particle swarm optimization algorithm with application to assembly line design.Applied Soft Computing Journal,vol.11,no.1,pp.605-613.

Li,J.;Fu,K.;Guo,J.B.;Zhang,Z.Q.;Xu,M.X.(2017):Establishment and optimization of a driving speed model for shield tunneling in mixed ground.Modern Tunnelling Technology,vol.54,no.3,pp.142-147.

Liu,H.;Cai,Z.;Wang,Y.(2010):Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization.Applied Soft Computing Journal,vol.10,no.2,pp.629-640.

Miao,A.;Shi,X.;Zhang,J.;Wang,E.;Peng,S.(2009):A modified particle swarm optimizer with dynamical inertia weight.Advances in Intelligent ＆Soft Computing,vol.62,pp.767-776.

Moeinossadat,S.R.;Ahangari,K.;Shahriar,K.(2017):Control of ground settlements caused by EPBS tunneling using an intelligent predictive model.Indian Geotechnical Journal,vol.2017,no.5,pp.1-10.

Mou,Y.T.(2013):Prediction and Control of Ground Surface Settlement Due to EPB Shield Tunneling Using Nonlinear Method(Ph.D.Thesis).Central South University,Changsha.

Nie,S.;Wang,Y.;Xiao,S.;Liu,Z.(2017):An adaptive chaos particle swarm optimization for tuning parameters of PID controller.Optimal Control Applications ＆Methods,vol.38,no.2,pp.1091-1102.

Pluhacek,M.;Senkerik,R.;Davendra,D.;Oplatkova,Z.K.;Zelinka,I.(2013):On the behavior and performance of chaos driven PSO algorithm with inertia weight.Computers and Mathematics with Applications,vol.66,no.2,pp.122-134.

Preisig,G.;Dematteis,A.;Torri,R.;Monin,N.;Perrochet,P.(2014):Modelling discharge rates and ground settlement induced by tunnel excavation.Rock Mechanics ＆Rock Engineering.vol.47,no.3,pp.869-884.

Razavialavi,S.R.;Abourizk,S.(2017):Site layout and construction plan optimization using an integrated genetic algorithm simulation framework.Journal of Computing in Civil Engineering,vol.31,no.4,04017011.

Sedghizadeh,S.;Beheshti,S.(2018):Particle swarm optimization based fuzzy gain scheduled subspace predictive control.Engineering Applications of Artificial Intelligence,vol.67,pp.331-344.

Seyedpoor,S.M.;Salajegheh,J.;Salajegheh,E.(2012):Shape optimal design of materially nonlinear arch dams including dam-water-foundation rock interaction using an improved PSO algorithm.Optimization ＆Engineering,vol.13,no.1,pp.79-100.

Shi,Y.;Eberhart,R.(1998):A modified particle swarm optimizer.Proceedings of the IEEE International Conference on Evolutionary Computation.

Taherkhani,M.;Safabakhsh,R.(2016):A novel stability-based adaptive inertia weight for particle swarm optimization.Applied Soft Computing,vol.38,pp.281-295.

Tran,T.H.;Hoang,N.D.(2016):Predicting colonization growth of algae on mortar surface with artificial neural network.Journal of Computing in Civil Engineering,vol.30,no.6,04016030.

Uma,S.M.;Gandhi,K.R.;Kirubakaran,E.(2012):A hybrid PSO with dynamic inertia weight and GA approach for discovering classification rule in data mining.International Journal of Computer Applications,vol.40,no.17,pp.32-37.

Yang,Y.;Tan,Z.S.;Peng,B.;Li,J.P.;Wang,G.(2017):Study on optimization boring parameters of earth pressure balance shield in water-soaked round gravel strata.China Civil Engineering Journal,vol.50,no.S1,pp.94-98.

Yazdani,D.;Sepasmoghaddam,A.;Dehban,A.;Horta,N.(2016):A novel approach for optimization in dynamic environments based on modified artificial fish swarm algorithm.International Journal of Computational Intelligence and Applications,vol.15,no.2,1650010.

Zhang,L.P.;Yu,H.J.;Hu,S.X.(2003):A new approach to improve particle swarm optimization.Lecture Notes in Computer Science,vol.2723,no.2,pp.134-139.

Zhou,C.;Ding,L.Y.;He,R.(2013):PSO-based Elman neural network model for predictive control of air chamber pressure in slurry shield tunneling under Yangtze River.Automation in Construction,vol.36,no.15,pp.208-217.