基于影响矩阵法及序列二次规划法的斜拉桥自动调索

郑 晖

（大连广播电视大学，辽宁 大连 116021）

0 引言

成桥合理状态是斜拉桥设计过程中需要确定的一个非常重要的结构受力问题，也是判断斜拉桥设计好坏的一个重要标准。现代斜拉桥结构类型多为高次超静定结构，索力的大小及其变化对成桥状态下的主梁、主塔等结构的受力影响很大。斜拉桥的拉索索力在恒载作用下可以调节，在斜拉桥结构布置已经确定的情况下，通过调整索力便可以找到一组索力使结构反映受力性能的指标达到最优。因而，斜拉桥的索力优化便成为合理成桥状态确定过程中的关键问题。

国内外学者对斜拉桥索力优化理论做了大量卓有成效的研究[1-7]，提出了许多的方法。于玲[1]等采用了基于复合约束的最小能量法，运用显示梯度的数学表达式进行求解。黄庆祥[2]采用大型通用有限元程序Midas/Civil，利用零位移法对某斜拉桥进行合理成桥状态分析。陈从春[3]等提出了基于拉索和预应力钢筋费用最小的索力优化方法，用大型有限元软件ANSYS和APDL语言实现了这一功能并进行了实桥验算。姜涛等[4]提出采用基于应力可行域法的斜拉桥合理成桥状态确定方法，以主梁恒载的应力可行域来控制斜拉桥成桥状态下主梁的受力状态，可以简单直观地判断出主梁的受力是否满足要求。阴文蔚[5]以全桥主梁所配预应力筋总量最少为目标函数，以恒活载共同作用下的塔梁索的应力作为约束条件，并采用约束变尺度法进行求解的应力优化法。

上述研究所提出的方法均未能全面考虑主梁桥塔和斜拉索在恒载作用下的变形及受力状态，且按单一的计算方法进行计算，计算过程比较繁琐，且都有局限性。鉴于此本文以影响矩阵理论为基础通过有限元软件对桥梁结构进行静力分析得到符合线性叠加理论的影响矩阵建立斜拉桥调索分析的优化数学模型，然后利用序列二次规划算法探索一种高效自动地索力优化的方案。最后将此方法运用于某斜拉桥有限元分析中经计算验证了该调索方法的有效性。

1 影响矩阵法的基本原理

斜拉桥结构的索力优化需要能考虑各种因素的影响，又能兼顾多种目标函数，基于此想法，同济大学肖汝诚[8]将广义影响矩阵的概念引入斜拉桥的索力优化中，提出了影响矩阵法。一般在有限元分析的基础上，基于建立好的有限元模型，以单位荷载的施调向量作用于模型上，获得结构状态（受调向量{A})和在索力(施调向量{X}）作用下的影响矩阵{B}，并以结构状态（结构线性、内力及支座反力等）表达式构建目标函数和约束条件的表达式，进行优化求解。

2 斜拉桥成桥索力优化模型的建立

斜拉桥索力优化的目的是使斜拉桥成桥状态合理，包括受力状态合理和线性状态合理。前者是指主梁、桥塔、斜拉索及桥墩等的受力状态下斜拉桥的力学性能能满足承载能力极限和正常使用极限的要求，且各项指标分布均匀；后者是要求保证主梁的成桥线型合理。此外，考虑经济原因的要求，还需在上述两者成立的情况下总造价接近最小。

一般不等式约束优化问题可表示为：

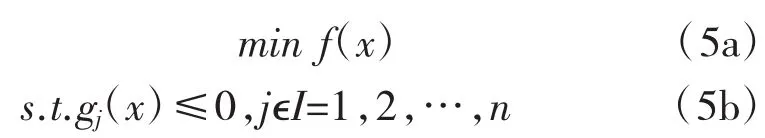
式中：f（x）为目标函数；x为设计变量；I为下标合集；gj（x）为约束函数；j为对约束函数的编号。

（1）目标函数选取：由于合理成桥状态量中，受力状态起关键作用，故目标函数选为主梁应变能和桥塔应变能之和。这项指标达到最小不仅可以考虑主梁和桥塔的弯矩，还可以全面表结构的位移和内力状态，使优化后得到的整个结构内力分布均匀并且达到最小值。通过有限元离散模型来建立目标函数如下：

式中：n为结构单元总数；X为拟调向量，本文选取索力为拟调向量；CL、CR分别表示索力对左右端弯矩的影响矩阵；Li、Ei、Ii分别表示i号单元的杆件长度、弹模、截面惯性矩；MLi、MRi分别表示调索后单元的左右端弯矩；ML0、MR0分别表示调索前单元的左右端弯矩。

（2）约束条件的选取：首先考虑斜拉桥中最重要的斜拉索其强度和疲劳的问题，对索力最大最小限值进行规定，且考虑实际工程意义，拉索的初始张拉力及正常使用过程中的索力都应为正值。其次，斜拉桥各结构构件的计算变形情况能较直接地反应斜拉桥的设计的合理性，因此对桥塔的塔顶进行横向位移约束，桥塔可以向岸侧留有一定的预偏值，主梁与斜拉索相交的位置应进行竖向位移约束。

式中：gj（x）为约束函数；j为对约束函数的编号。

3 基于序列二次规划算法的自动调索和技术路线

求解约束优化问题的算法中序列二次规划法是最有效的算法中的一种，自从Wilson首次提出此方法以来，国内外学者对其进行了广泛和深入的研究。本文拟采用基于可行方向法结合序列二次规划法的强次可行SQP法[9]进行优化求解，该算法保证有限次迭代计算后，迭代点进入可行域。通过构造了一个Armijio曲线搜索和两个由含相同逆矩阵构造的新的显示修正方向，减少了算法的迭代计算量，其算法原理如下：

对于第k个迭代点xkєRn，作如下记号和定义。

（1）可以通过求解公式（13）的二次规划子问题，来求解不等式约束优化问题（5），最终得到主搜索方向。

式中：BkєRnxn是问题（5）的拉格朗日函数在xk处的Hessen阵的近似。

（2）由于问题（13）总有可行解d=0,是其最优化解，但其不一定是一个可行方向，本算法中利用广义投影技术求得新的改进显示修正方向dk,并给出新的高阶显示修正方向d~k，具体计算公式详见文献[9]。

（3）设计变量的迭代公式为

式中:步长λk通过构建的一个新型Armijio曲线搜索得到。

（4）当（，φk）=（0,0）时，xk是问题（5）的最优解。

如上所述，斜拉桥设计中斜拉桥的索力优化是其关键问题，也是进行全桥内力分析的必要前期工作。利用强次可行SQP法建立数学规划模型来进行斜拉桥索力自动优化求解，可大幅度减少手算的工作量和盲目性，实现高效的全局最优求解。且通过MIDAS的建模功能与EXCEL的交互处理，可方便的实现算法的自动优化求解[10]，技术路线及具体的流程见图1。

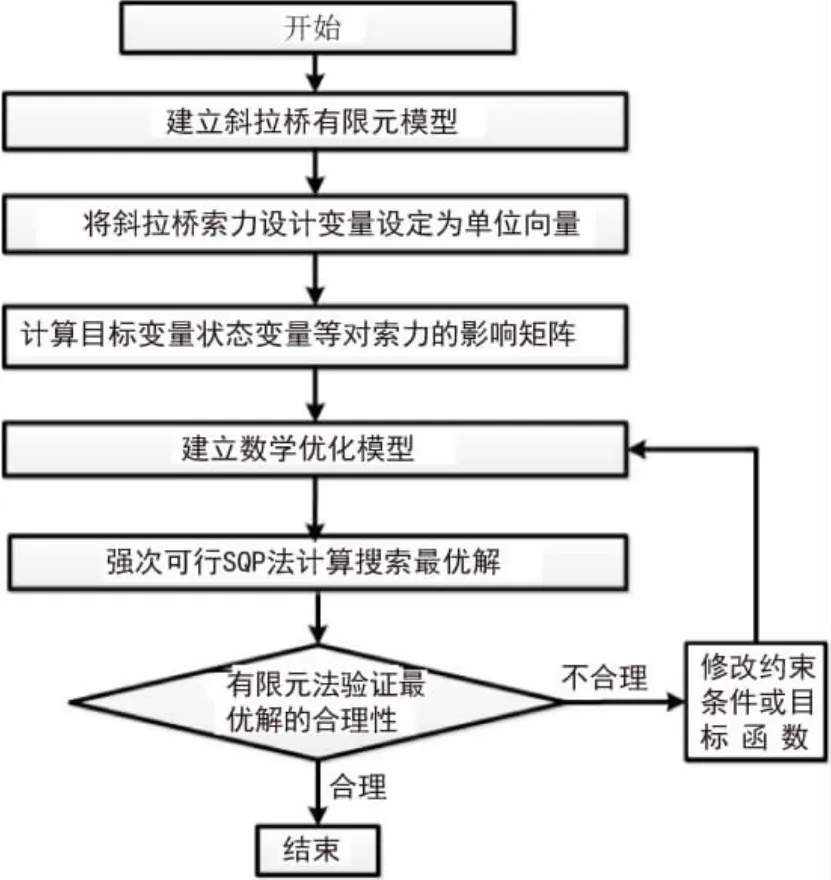
图1 计算流程图

4 工程算例

4.1 工程概况

以某双塔单索面三跨混凝土斜拉桥为研究对象，桥梁全长265 m，桥跨布置为70 m+125 m+70 m。斜拉索采用扇形布置，共24根索。采用板式边主梁的主梁截面形式，主梁截面宽度35 m，端部高度1 m，桥塔采用变截面空心箱形截面，材料均选用混凝土，具体特性见表1。

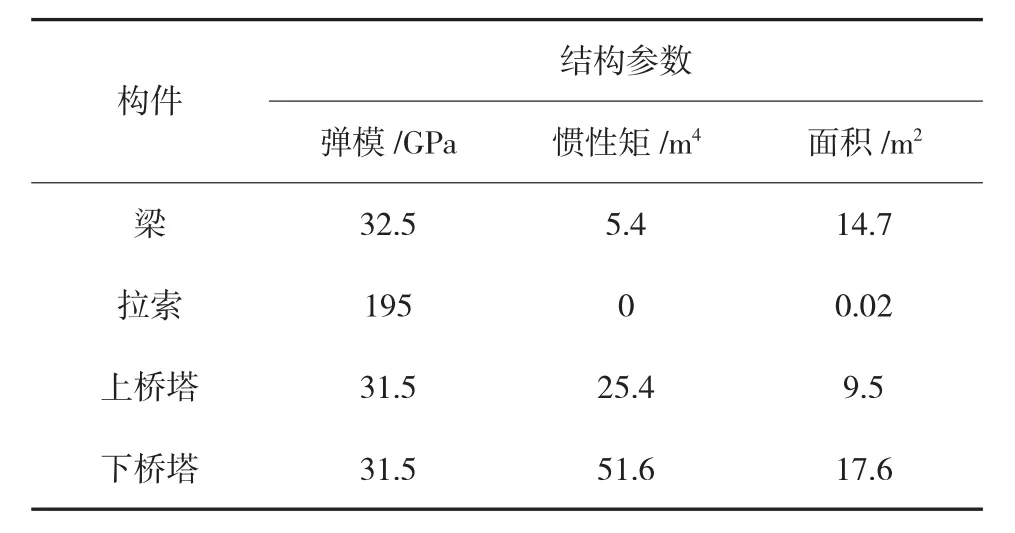
表1 构件材料特性、几何特性表

4.2 计算模型

选用MIDAS/CIVIL建立斜拉桥有限元模型，全桥采用鱼骨模型。共有69个节点，66个梁单元，24个桁架单元。边界条件采用固定边界，斜拉桥布置见图2，拉索从左到右依次编号为T6～T1，T7～T12，T12～T7，T1～T6。建模过程将主梁单元长度划分为一致，可以减少后续工作的计算量。

图2 斜拉桥立面布置

优化目标函数选取成桥主梁和桥塔的弯曲应变能之和，约束条件为索力范围采取规范要求的材料上下极限，主梁与斜拉索交点的竖向允许位移为10 mm，桥塔塔顶变位合理,设定顺桥向允许位移为10 mm。

4.3 结果分析

由于结构对称，仅取一半结构进行分析，经过优化计算得到主梁与桥塔的最小弯曲应变能之和最小时的成桥索力，优化前后索力对比见图3。

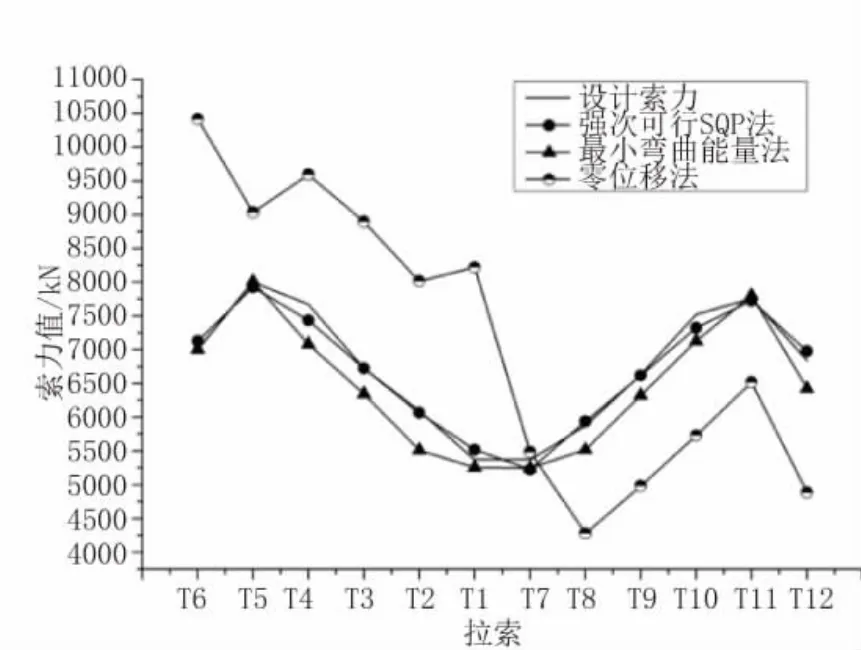
图3 优化前后索力对比

由图3可以看出强次可行SQP法与最小弯曲能法计算出的索力与设计索力分布较为吻合，零位移法计算得到的索力，整体分布不均匀，且同设计索力相差较大。其中强次可行SQP法计算得到的索力最为合理，从短索至长索索力逐步增大，最大索力为边跨第5号索，值为7 926 kN，最小值发生于中跨第7号索，索力5 225 kN，所得索力与设计索力一致且偏差较小，基本差值在5%以内。

最优成桥状态主梁弯矩见图4。由图4可以看出三种算法整体主梁弯矩分布都较均匀，零位移法由于仅考虑拉索和主梁交点处位移为零，故在靠近主塔部位主梁弯矩有较大突变。最小弯曲能量法是无约束的优化方法，仅考虑全桥弯曲能量最小，相较于强次可行SQP法计算得到的弯矩，整体偏大，后者主梁所受弯矩整体分布均匀且较小，拉索范围内主梁弯矩值均在5 000 kN·m内，此种受力状态可以充分的保证主梁的承载能力和跨越能力。最大弯矩处于拉索范围外，未经过拉索调节，工程中一般通过在主梁端部添加辅助墩来减小弯矩突变。

图4 优化后主梁弯矩

桥梁的主塔作为受压构件，索力优化后，其受力接近于轴压状态，减少其因局部弯矩过大而造成的破坏，桥塔弯矩如图5所示。最小弯曲能量法和零位移法由于仅考虑主梁的目标优化，故计算得到的主塔塔根弯矩偏大，受力不均匀，最大塔根弯矩分别达1 500 kN·m和3 600 kN·m。强次可行SQP法计算得到主塔弯矩较小，主塔受力状态接近轴压状态，最大塔根弯矩为-479.56 kN·m，相较前两种算法大大减小。

最终成桥状态主梁竖向位移见图6。由图6可知，由于零位移法其优化目标便是主梁节点位移为零，故其竖向位移分布接近于零轴。强次可行SQP法和最小弯曲能量法计算得到的主梁位移图对比，两者主梁均有向下的挠度，前者最大挠度为5.5 mm，后者最大值为9.6 mm，均小于约束条件中设定的10 mm限值。但是整体变形情况，前者比后者小且均匀。

图5 桥塔轴力图

图6 主梁竖向位移

5 结语

本文以精确性、高效性为原则，便于工程实用性为目的，基于响应矩阵原理结合序列二次规划法求解斜拉桥的索力优化问题，结果表明优化过程稳定、高效、无需人工干预便可获得合理的拉索拉力，索力分布均匀，基本随着长度增长。弯曲应变能作为目标函数并考虑多种不同的约束工况，更全面的考虑了整体结构对拉索索力的影响，优化结果主梁线性平顺，主梁内力均匀且符合规范要求，主塔充分发挥受压能力。本文方法简单、有效，可较容易实现程序化，可以为同类型的斜拉桥索力优化提供一种新的求解方案。