大果紫檀表面润湿渗透方程的构建与计算比较

秦志永，莫柳婷，卢禹彤，冯小琼，廖木荣，牟继平

（广西大学 资源环境与材料学院，广西 南宁 530004）

接触角技术是研究固体表界面润湿性能最成熟的方法之一，通过简单地测量形成于液体、气体和固体的交叉几何角，直接就实现了对固体表界面润湿性能的计算与评估[1]。就木材而言，表界面润湿渗透特性与其表面吸附、涂饰、染色、耐老化以及表面胶合等性能密切相关，是木材表界面特性中最重要的参数之一[2]。

红木纹理美丽，稳定性好，属珍贵木材，制作的家具名贵高雅，色泽迷人，牢固耐用，颇受人们青睐，其表面加工处理也越来越受关注[3]，因此研究红木的表面润湿渗透特性，对红木表面涂饰及表面保护具有重要意义。在对木材表面润湿特性的研究中，研究者们采用了不同时间节点的接触角以及润湿率为0时的恒定润湿角等静态接触角来描述木材表面的润湿性[4-5]；研究者们也尝试了构建各种线性[4]或非线性润湿动态方程[6-7]，计算获得整个过程的润湿速率，研究了液体在木材等生物质材料表面的润湿过程。

目前，对红木的研究多局限于视觉特性、环境学特性、化学特性等领域[8-10]，针对大果紫檀以及其他红木的表面润湿渗透性的研究鲜见报道。本文以大果紫檀为例，分别选取其径切面顺纹、横纹方向，弦切面顺纹、横纹方向为研究对象，采用线性方程、S-G方程及并构建新的动态润湿方程计算水在其表面的润湿特性，比较不同润湿方程对表面润湿渗透特性的计算差异，为红木表面涂饰及保护提供理论指导依据，也可为其他生物质材料的润湿渗透性研究提供参考。

1 材料与方法

1.1 试验材料

大果紫檀产自缅甸，气干密度为0.86 g/cm3，试件尺寸为100.0 mm×50.0 mm×15.0 mm。将试件置于温度为25±2℃、湿度为57±2%RH环境下均衡处理15 d以调节其含水率，取径切面与弦切面的顺纹、横纹为测试对象。木材的含水率、表面粗糙度、老化特性等因素都会影响接触角，测试过程中，要保证试件表面特性、处理条件、测试环境一致性。

试验试剂为蒸馏水（实验室自制），表面张力为72.8 N/m。

试验设备为体视显微镜（德国卡尔·蔡司公司SteREO Discovery.V20）；接触角测定仪（德国DSA 100E KRÜSS）。

1.2 试验方法

1.2.1 宏观构造图像

将试件置于载物台上，选择20×放大倍数，调整镜头高低和焦距、入射光源等使得CCD成像系统获取最清晰的试样图像，拍摄大果紫檀径切面和弦切面图像，测试条件为温度20±2℃、湿度57±2%。

1.2.2 接触角测定

采用接触角测定仪测量蒸馏水在大果紫檀不同表面的接触角。将蒸馏水抽入注射器后滴在试件表面，液滴大小为5 μL。录制液滴开始到60 s的全过程，记录各时段的接触角，前10 s每1 s记录一次，10～60 s每10 s记录一次。测试3组试件，每组试件的弦切面横纹、弦切面顺纹、径切面横纹、径切面顺纹各取3个点（图1），每个切面纹理共9个点，取平均值。测试环境温度20±2℃、湿度57±2%。用Origin 8.5（美国OriginLab公司）软件进行数据处理。

图1 不同切面方向接触角图Fig.1 Diagrams of contact angle in different tangential directions

1.2.3 润湿渗透方程

1）线性方程。将水在木材表面的润湿行为分成铺展和渗透两个阶段：

铺展阶段（0～5 s），方程表示为：

式中：a1表示铺展阶段初始接触角，b1表示铺展速率。

渗透阶段（10～60 s），其方程表示为：

式中：a2表示渗透阶段初始接触角，b2表示渗透系数。

整个阶段（0～60 s），润湿方程表示为：

式中：a0表示整个阶段初始接触角，b0表示润湿速率。

2）S-G方程。Shi和Gardner以相对接触角减少速率为基础，提出一种润湿方程（S-G 方程）[6]，研究了酚醛树脂和异氰酸酯在不同木材早晚材表面润湿性，该方程常用于评估木材等生物质材料的动态润湿过程[11-15]，如公式（4）所示：

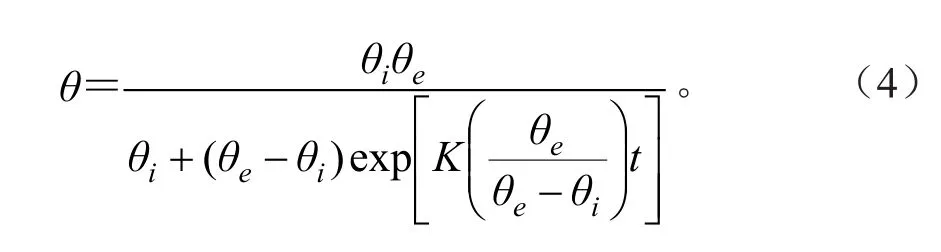
式中：K为渗透系数，表示试液在木材表面渗透和扩展快慢速率，K值越大，液滴的渗透和扩散速率越快，θ为接触角，时间为t，θi初始接触角，θe为平衡接触角。

3）润湿方程的构建。结合S-G等润湿方程，本研究成员提出一个较为简单的动态润湿性能表征计算公式，见公式（5）所示：

式中：θ为接触角，K为渗透系数，时间为t，A表示与初始接触角和平衡接触角相关的限制条件，当时间t为0时，A+B是初始接触角，当t为无穷大时，B为平衡接触角。

2 结果与分析

2.1 大果紫檀不同切面宏观构造分析

图2为大果紫檀径切面和弦切面的宏观构造图像。由图2可知，大果紫檀径切面结构纹理较致密，木射线细胞中含深色沉积物，会导致蒸馏水不易渗透入木材中；弦切面较粗糙，具有较明显的孔洞和疏松的导管沟槽，木材中的沉积物和结构差异均会对木材表面的润湿渗透性造成影响。

图2 大果紫檀宏观构造图像Fig.2 Macrostructure of P.macrocarpus

2.2 线性方程计算大果紫檀的润湿特性

图3为线性方程拟合所得大果紫檀不同切面纹理的接触角随时间的变化。由图3和表1可得，整个润湿阶段（即0～60 s），大果紫檀径切面顺、横纹及弦切面顺、横纹的润湿渗透系数分别为0.79，0.31，0.70和0.52，表明其径切面顺纹的润湿渗透性能最好。分段角度讨论，铺展阶段的曲线斜率均远大于渗透阶段，表明木材的铺展速率比渗透速率大的多，由于木材为一种多孔性材料，由于毛细管作用，水在其表面并迅速扩散，液滴下的木材会吸水膨胀, 使得木材表面结构发生变化，另外木材表面快速吸水导致液滴部位的木材含水率增加，木材表面亲水性的羟基逐渐增加，铺展过程较快；在10～60 s渗透阶段，水开始渗透其表面，当逐渐饱和时，吸水变缓，渗透速率下降，最后逐渐达到相对平衡状态。在铺展阶段（0～5 s），水在木材弦切面上的铺展速率大于径切面，顺纹大于横纹。水在木材表面渗透阶段（10～60 s）及整个润湿阶段（0～60 s），润湿规律一致，顺纹的润湿速率大于横纹，径切面顺纹大于弦切面顺纹，而弦切面横纹大于径切面横纹。就整个润湿阶段而言，由于润湿曲线可知，变化规律并非是线性的，因此拟合所得R2分别为0.86，0.87，0.83和0.84，均小于0.90，拟合系数相对较低。

2.3 S-G方程表征大果紫檀的润湿特性

图4为S-G方程拟合所得液滴在木材表面的接触角随时间变化的拟合曲线。在计算过程中，所采用初始接触角为0 s的接触角（液滴接触角木材表面相对稳定的第一个角度），60 s时的接触角为平衡接触角。由图4可得，木材径切面顺、横纹，弦切面顺、横纹的渗透系数分别为0.039, 0.015,0.049和0.027，弦切面的渗透系数较径切面高，表明弦切面的润湿渗透性能较好，是由于大果紫檀径切面含大量纹孔结构和木射线，纹孔孔口被纹孔膜堵塞，纹孔膜阻碍蒸馏水在径切面的渗透，减小径切面中的有效渗透路径，径切面中的射线细胞大多是封闭细胞，在一定程度上阻碍蒸馏水渗透。顺纹的渗透系数较横纹的高，同时径切面、弦切面顺纹方向平衡接触角分别为61.95°及52.52°，径切面、弦切面横纹方向平衡接触角分别为95.42°及80.71°顺纹方向平衡接触角小于横纹方向平衡接触角，表明顺纹的润湿渗透性能较好，在解剖结构上，导管和轴向薄壁组织在木材中均为纵向排列有利于液体顺着纤维渗透和扩散，而横向纤维的液体渗透会受到细胞壁的阻隔，此外木射线在弦切面叠生、多列排列，有利于水在弦切面顺纹方向上的润湿、渗透（图2）。采用S-G方程进行拟合，R2分别为0.99，0.95，0.98和0.97，均大于0.95，表明S-G方程拟合度较高，拟合效果较线性方程好，同时也得出与线性方程不一致的润湿规律。

图3 线性方程计算所得接触角随时间变化规律Fig.3 Variation of contact angle calculated by linear equation with time

表1 不同切面纹理的线性方程Table 1 Linear equations of different surface textures

2.4 新构建润湿方程表征大果紫檀的润湿特性

图5为新构建的润湿方程拟合所得大果紫檀不同切面接触角随时间变化的拟合曲线。由图5可看出，大果紫檀径切面顺纹、横纹及弦切面顺纹、横纹的渗透系数分别为0.06, 0.061、0.079和0.074（表2），表明其弦切面的润湿速率大于径切面，顺纹的润湿速率大于横纹，这均与S-G方程所得结论完全一致。拟合度R2分别为0.99、0.97、0.98和0.99，拟合度比线性方程和S-G方程略高，能准确计算水在木材表面的润湿渗透速率。

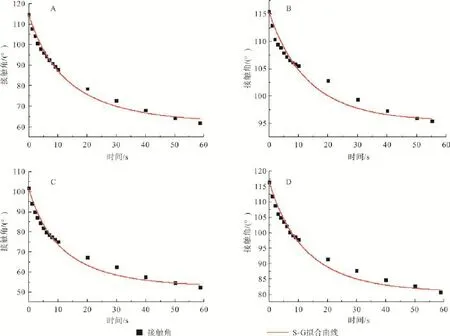
图4 S-G方程计算所得接触角随时间变化规律Fig.4 Variation of contact angle calculated by S-G equation with time

3 结论与讨论

线性方程描述了液滴在木材表面接触角随着时间变化的两个阶段：铺展阶段接触角随时间变化速率几乎恒定，为线性变化；渗透阶段接触角随时间变化相比于铺展阶段较慢，直到水几乎全部吸收达到恒定，也为线性变化。在以往相关研究中，Santoni等采用0～5 s和100～150 s两段研究了水在不同木材表面润湿渗透行为[4]，曹金珍等也采用0～10 s阶段的润湿行为，研究了水在未处理材和水基防腐处理材表面的接触角的变化趋势[16]。通过将铺展阶段、渗透阶段及整个润湿阶段进行线性拟合，可以较好的分析水在木材表面的铺展和渗透行为，但是两个阶段时间范围很难被界定，人为因素影响较大，该方程的准确性需要进一步解释和完善。

采用S-G方程中的润湿系数K表征大果紫檀表面动态润湿性，拟合度较高，拟合效果较线性方程好，在已有的研究报道中，S-G方程常用于评估木材等生物质材料的动态润湿过程[11,13-15]，笔者也曾利用该方程研究了砂光和老化处理木材表面的润湿特性[12]，但由于木材是一种多孔性生物质材料，其初始接触角和平衡接触角很难确定，且计算过程比较复杂。

就新构建的方程而言，蒸馏水在大果紫檀表面理论上的初始接触角和平衡接触角可由该方程确定，当时间为0时得到初始接触角，当时间趋于无穷大时得到平衡接触角。与S-G方程计算过程所使用的初始接触角相比，理论所得初始接触角要小，原因是，最初液滴在木材表面并未处于平衡状态，即认为液滴在木材表面接触角产生的第一个角度就是初始接触角，是人为界定，往往该角很难被准确捕捉，造成误差较大，通过新构建的方程获得理论平衡接触角，且比与S-G方程计算过程所使用的平衡接触角要大，这主要由于新构建方程根据润湿曲线假定润湿行为的最终阶段为平衡阶段，接触角不再发生任何变化，实际上水在木材表面的接触角会随着时间的延续而不断降低，只能获得理论上的平衡接触角。新构建润湿方程在不确定初始接触角和平衡前提下，可用于评估动态润湿性，通过该方程还可确定理论初始接触角和平衡接触角，且在本研究中拟合度最高。

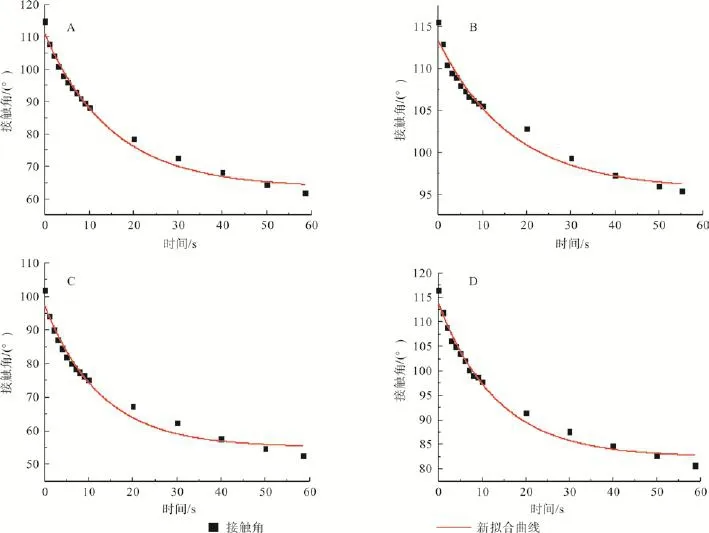
图5 新构建的润湿方程计算所得接触角随时间变化规律Fig.5 Variation of contact angle calculated by newly constructed wetting equation with time

表2 新构建润湿方程获得不同切面纹理的初始和平衡接触角及K值Table 2 Initial and equilibrium contact angles and K values of different surface textures

在以往研究所采用的动态润湿方程中，都不可避免采用了初始接触角或平衡接触角，由于木材表面结构复杂，同时受到测试仪器精密程度和人为因素的影响，初始接触角很难被准确确定；此外，由于木材的多孔性、各项异性以及表面固有的亲水基团等因素，使得液体在其表面总会出现接触角滞后现象，在假定没有蒸发现象发生时，接触角会随着时间地延续而不断变小，真正的平衡接触角很难获得。与现有的几种方程相比，新构建的润湿方程不仅可确定润湿渗透速率，且不需人为确定初始接触角和平衡接触角，已经证实该方程在研究胶粘剂在杨木表面的润湿渗透特性有较好的适用性[12]。本研究也可为其他生物质材料的润湿渗透性研究提供参考，但该方程在木材等生物质材料表面的适用性需要进一步解释和验证。

综上所述，线性方程所得径切面顺纹渗透系数最大，S-G方程所得弦切面的润湿速率大于径切面，顺纹的润湿速率大于横纹，新构建润湿方程所得规律与S-G方程一致；3种润湿方程均可计算大果紫檀表面润湿渗透系数；线性方程能揭示润湿和渗透过程，但人为因素影响较大；S-G方程能描述整个润湿过程且拟合度较高，但计算过程较为复杂，同时需要已知初始接触角和平衡接触；新构建的润湿方程计算简便，拟合度更高且能够获得润湿过程中初始接触角及平衡接触角，适合表征液体在木材表面的润湿渗透特性。