混合润滑下弧齿锥齿轮啮合路径对传动及接触特性的影响*

汪巨基，蒲 伟，王家序,2，曹 伟，任 思

1.四川大学 空天科学与工程学院, 成都 610065；2.重庆大学 机械传动国家重点实验室, 重庆 400044.

0 引 言

弧齿锥齿轮广泛应用在航空、船舶及汽车等领域，用于传递交错轴间的运动及动力，其动态接触特性是影响传动平稳性、振动、噪声等的重要因素[1].受齿面粗糙度的影响，弧齿锥齿轮大多工作在粗糙峰接触与润滑油膜共存的混合润滑状态，因此深入研究混合润滑状态下弧齿锥齿轮接触特性具有重要意义.

早期侧重于无润滑条件下的动态接触特性研究，HANDSCHUH等[2]实验研究了弧齿锥齿轮动态接触下的齿根弯曲应力，得到齿根弯曲应力的变化规律，并与准静态有限元分析结果进行对比.LI[3]在考虑加工和安装误差的情况下，利用有限元法计算出齿面接触力和齿根弯曲应力.SIMON[4]研究了机床调整参数和刀具几何参数对于弧齿锥齿接触压力和承载传动误差的影响.唐进元等[5]建立了加载接触分析模型，重点分析齿面接触强度及应力沿齿面的分布状况，为弧齿锥齿轮动态啮合方面的研究提供了理论依据及分析方法.侯祥颖等[6]建立了弧齿锥齿轮高精度有限元模型，研究接触应力和接触印痕的变化.苏宇龙[7]研究了安装位置对齿面接触印痕的影响，得到三种安装误差的合理调整会达到优化接触的效果，但调整值较小，未能涵盖弧齿锥齿轮从大端到小端的接触.

随着摩擦学的研究和发展，摩擦对动态特性的影响逐渐受到关注，开始了考虑润滑状态的弧齿锥齿轮接触特性研究.关于弧齿锥齿轮摩擦系数的计算，大多数研究基于多参数拟合的经验公式，如BENEDICT等[8]和XU等[9]均推导出摩擦系数经验公式，经验公式能够简化摩擦系数计算过程，但考虑的参数有限，适用范围也存在局限，无法反映真实接触情况下的摩擦系数.祝政委[10]运用动力学原理，考虑到摩擦系数对运动特性和齿面接触力的影响，结论指出摩擦系数差异对啮合面接触力的影响不大.刘光磊等[11]用数值方法研究动态响应下摩擦系数对齿面啮合轨迹的影响，指出摩擦系数影响齿轮位移，对齿面啮合轨迹影响不大.

鉴于现有研究未综合考虑真实摩擦环境及接触区位置对于弧齿锥齿轮接触特性的影响，本文旨在采用混合润滑模型研究一对弧齿锥齿在不同啮合路径下的摩擦系数变化情况，同时与传统经验公式计算结果对比.在此基础上，运用有限元软件研究不同啮合路径下动态传动误差和齿面摩擦力的变化，对弧齿锥齿轮轮齿表面摩擦学及啮合路径调整研究具有重要意义.

1 弧齿锥齿轮模型建立

1.1 几何模型

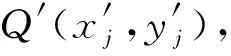
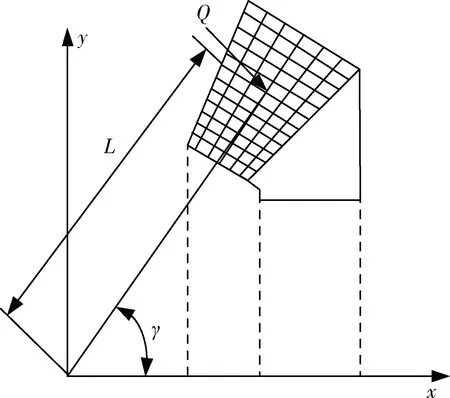
图1 齿面网格划分Fig.1 Mesh of tooth surface

1.2 啮合路径调整计算

理论上，弧齿锥齿大小齿轮的共轭点在大轮坐标系下应相互接触，理想接触区位于中间偏小端，但在实际安装过程中可能存在大小轮齿面在设计点处没有接触，需将小轮相对于大轮移动ΔRd，实际移动中将分别沿大小齿轮轴线方向和垂直两轴线的方向进行矢量移动，表示为

(1)

通过3个方向的微调整量实现共轭点的接触.调整量由式(2)计算得到，不同啮合位置示意图如图2所示.

(2)

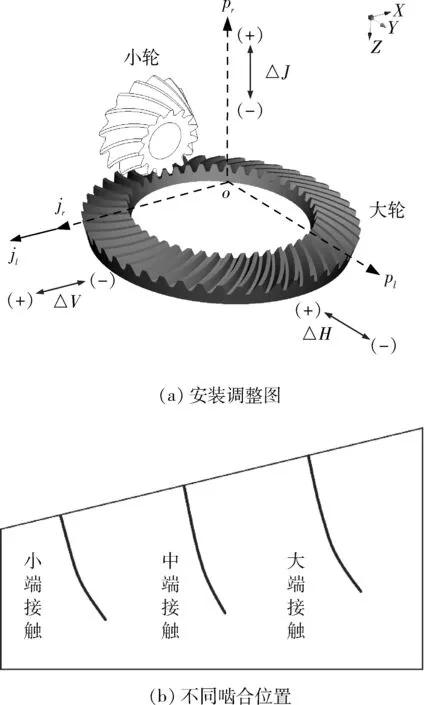
图2 啮合路径调整示意图Fig.2 Meshing path adjustment diagram

1.3 传动误差计算

传动误差能综合反映动态性能、重合度、齿面接触特性等信息，其幅值大小可反映接触路径上的制造及安装误差.弧齿锥齿轮的传动误差由式(3)计算：

(3)

1.4 齿面摩擦系数计算

弧齿锥齿轮混合接触润滑可简化为椭圆接触模型，根据文献[13]建立的点接触润滑Reynolds方程：

(4)

式中,θe为卷吸速度和接触椭圆短轴间夹角，p为椭圆区域内的压力分布，h为油膜厚度，η为润滑油粘度.将原压力粘度、压力密度、载荷平衡方程经过归一化改写后的方程如式(5)～(7)所示.

压力-粘度方程为

(5)

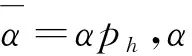
压力-密度方程为

(6)

载荷平衡方程为

(7)

对于模型中的摩擦力计算，采用Bair和Winer[14]建立的粘弹性非牛顿流体模型计算剪切应力的公式为

(8)

式中剪切模量G∞和剪切应力τL由Dyson经验公式[15]计算：

(9)

式中T为接触表面温度.

混合润滑模型的准确性已进行了验证[13]，本文主要将此混合润滑模型与传统经验公式计算结果进行对比，选择两个考虑参数较为完整的经验公式作为对照.

BENEDICT等[8]通过大量实验拟合出考虑多参数的摩擦系数计算公式

(10)

式中,W′为载荷，v为绝对速度，Vs为相对滑动速度，Vr为卷吸速度.

XU[9]将弧齿锥齿轮点接触简化为线接触，通过大量线接触混合润滑模型计算，利用多元线性回归拟合出摩擦系数计算公式：

(11)

其中

f(SR,Ph,η,S)=b1+b4|SR|Phlog10(η)+

b5e-|SR|Phlog(η)+b9eS(12)

式中,SR为滑滚比，Vr为卷吸速度，Ph为最大赫兹压力，S为粗糙度，R为曲率半径，η为润滑油粘度.润滑油相关系数b1-b9参见文献[9].

2 算例参数

本论文以某典型航空弧齿锥齿轮为分析对象，其具体的轮坯参数及机床加工参数如表1和2所示.

在实际过程中通过改变小轮的ΔV和ΔH值来调整不同的啮合位置.通过TCA计算得到不同啮合路径下的ΔV和ΔH值，如表3所示.

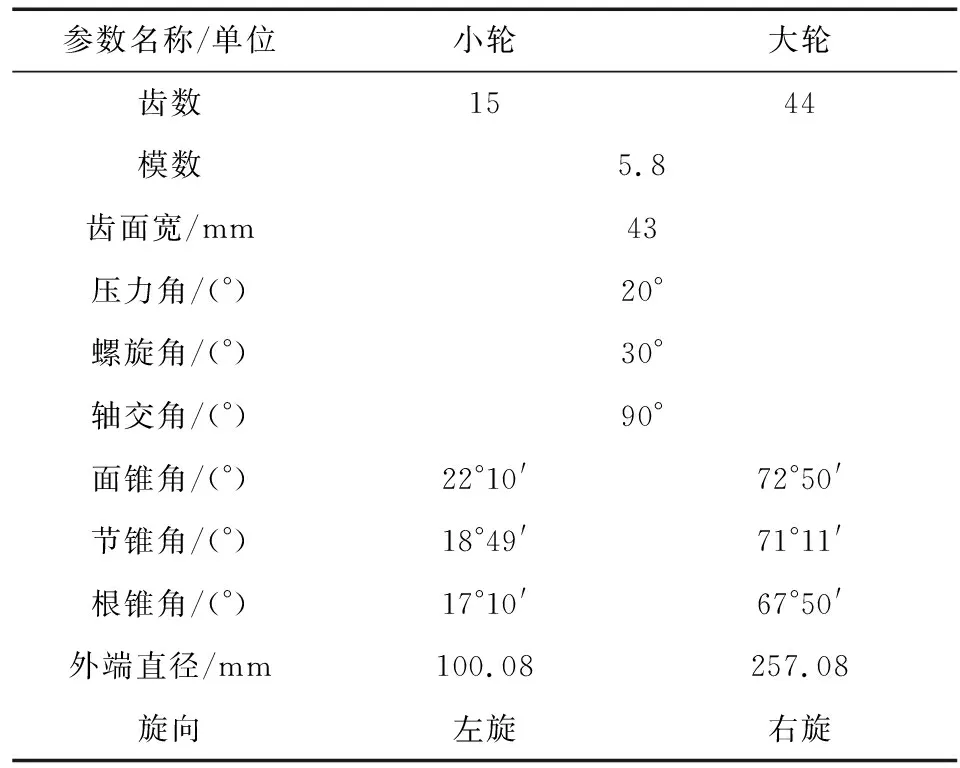
表1 轮坯参数Tab.1 Tooth blank

表2 机床加工参数Tab.2 Machine tool processing parameters

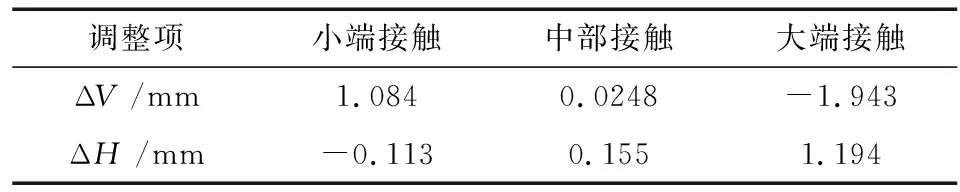
表3 不同啮合路径下的ΔV和ΔH值Tab.3 The values of ΔV and ΔH in different mesh paths

本文运用有限元法对弧齿锥齿轮全齿模型进行分析.将建立的模型导入Ansa软件中划分整齿网格，划分后模型共有476818个节点，368960个单元.导入ABAQUS中进行显示动态分析，设定大小轮材料相同，弹性模量为210 GPa，泊松比为0.3.运动分析中需要考虑质量、转动惯量和阻尼对齿轮模型的影响，材料密度为7.8×10-9t/mm3，阻尼选择Rayleigh阻尼.定义接触属性为面面接触，参考点选为各齿轮的质心，与齿轮内圈采用刚体耦合约束，对小轮添加恒定转速，对大轮施加阻力矩.

3 结果与讨论

3.1 摩擦系数求解对比

图3为不同啮合路径下3种摩擦系数求解方法得到的摩擦系数随大轮单齿啮合过程中的变化，工况设定大轮转速为1 000 r/min，转矩为250 N·m.

对比图3在不同啮合位置下的摩擦系数，可以看出BENEDICT等[8]的经验公式计算结果与混合润滑模型计算结果趋势相同，在大轮单齿啮合过程中摩擦系数先增大后减小，关于接触中点对称，在接触中点位置达到峰值，但BENEDICT等的公式计算结果摩擦系数偏小，且在中部接触的节锥母线附近增加迅速,这与文献[16]得到的摩擦系数变化趋势相对平滑的结论不一致.XU等[9]的经验公式计算结果在单齿啮合的啮入啮出阶段与混合润滑模型结果接近，在接触中点位置附近减小，公式中认为在接触中点附近相对滑动速度接近于零，这与弧齿锥齿轮在节锥母线附近依然存在滑动的实际不符.对比三者结果说明在节锥母线附近经验公式的摩擦系数求解误差较大.

研究不同啮合路径对弧齿锥齿轮传动误差和接触力的影响需考虑混合润滑状态下的摩擦特性.由图3可知，轮齿啮合过程中，摩擦系数波动变化较小，为了提高求解效率，假定摩擦系数为常数(平均摩擦系数).

图3 不同啮合位置摩擦系数对比Fig.3 Comparison of friction coefficient indifferent mesh paths

3.2 不同啮合路径下传动误差对比

图4所示为小端接触时考虑摩擦和不考虑摩擦情况下的传动误差图，两种情况下传动误差的变化趋势相同，但在考虑摩擦的情况下小端接触传动误差更小，说明润滑状态能够减小传动误差，使传动更平稳.

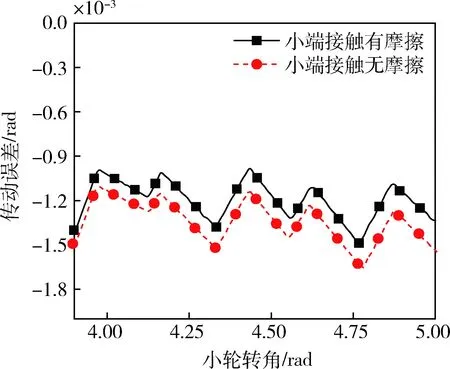
图4 小端接触时传动误差Fig.4 Transmission errors in the heel contact

图5所示为混合润滑状态下弧齿锥齿轮不同啮合路径下的传动误差，可以看出在不同啮合路径下，传动误差变化趋势基本相同.中部接触时传动误差最小，小端接触时传动误差最大，说明在混合润滑状态下中部接触时传动最平稳，小端接触时振动最大.因此为保证传动精度，实际安装过程中应尽量选择在中部接触，避免在小端接触.

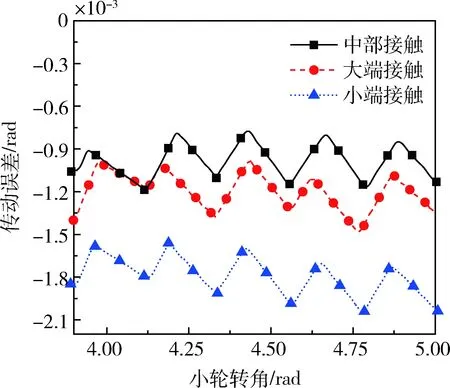
图5 不同啮合路径下传动误差Fig.5 Transmission errors in different mesh paths

3.3 不同啮合路径下接触力对比

图6所示为不同啮合路径下接触力云图对比，在不同啮合路径下接触力范围大小不同.与中部接触时接触力范围相比，大端接触时接触椭圆沿齿长方向较短，沿齿高方向较宽，小端接触时接触椭圆沿齿长方向较长，齿高方向较窄.比较不同啮合路径下的最大接触力，结果显示在大端接触时最大，中部接触和小端接触时的最大接触力相近，说明大端接触时需承受更大的齿面压力.

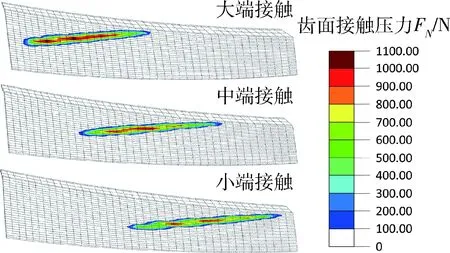
图6 不同啮合路径下接触力云图Fig.6 Contact force cloud picture underdifferent mesh paths

3.4 不同啮合路径下摩擦力对比

摩擦力影响齿轮接触过程中的磨损、温升等情况，摩擦力过大会导致齿轮接触性能变差.研究不同啮合路径对摩擦力的影响，对比不同啮合路径下齿面摩擦力的变化，如图7所示.可以看出不同啮合路径下摩擦力变化趋势相同，在啮入阶段先增大到峰值后开始减小，到接触中点位置附近发生转折，接触中点位置后摩擦力继续增大到最大值.不同啮合路径下的摩擦力最大值差距较小，而相比于大端接触和小端接触，中部接触时接触中点摩擦力很小，说明在中部接触的接触中点附近润滑状况较好，摩擦损失更少.

图7 不同啮合路径下摩擦力Fig.7 Friction forces under different mesh paths

为分析图7中显示的摩擦力变化趋势，对比小端接触时单齿啮合过程中总摩擦力与各个方向摩擦力的变化，如图8所示.图8中摩擦力合力输出为标量，三个方向分力为矢量，由图可以看出摩擦力合力在啮入啮出阶段主要受大轮坐标系下Z轴方向摩擦分力的影响，大轮坐标系下X方向和Y方向的摩擦分力对合力的影响较小.在节点附近由于相对滑动方向出现变向，Z轴方向摩擦分力减小且产生变向，影响摩擦力合力减小且出现转折.

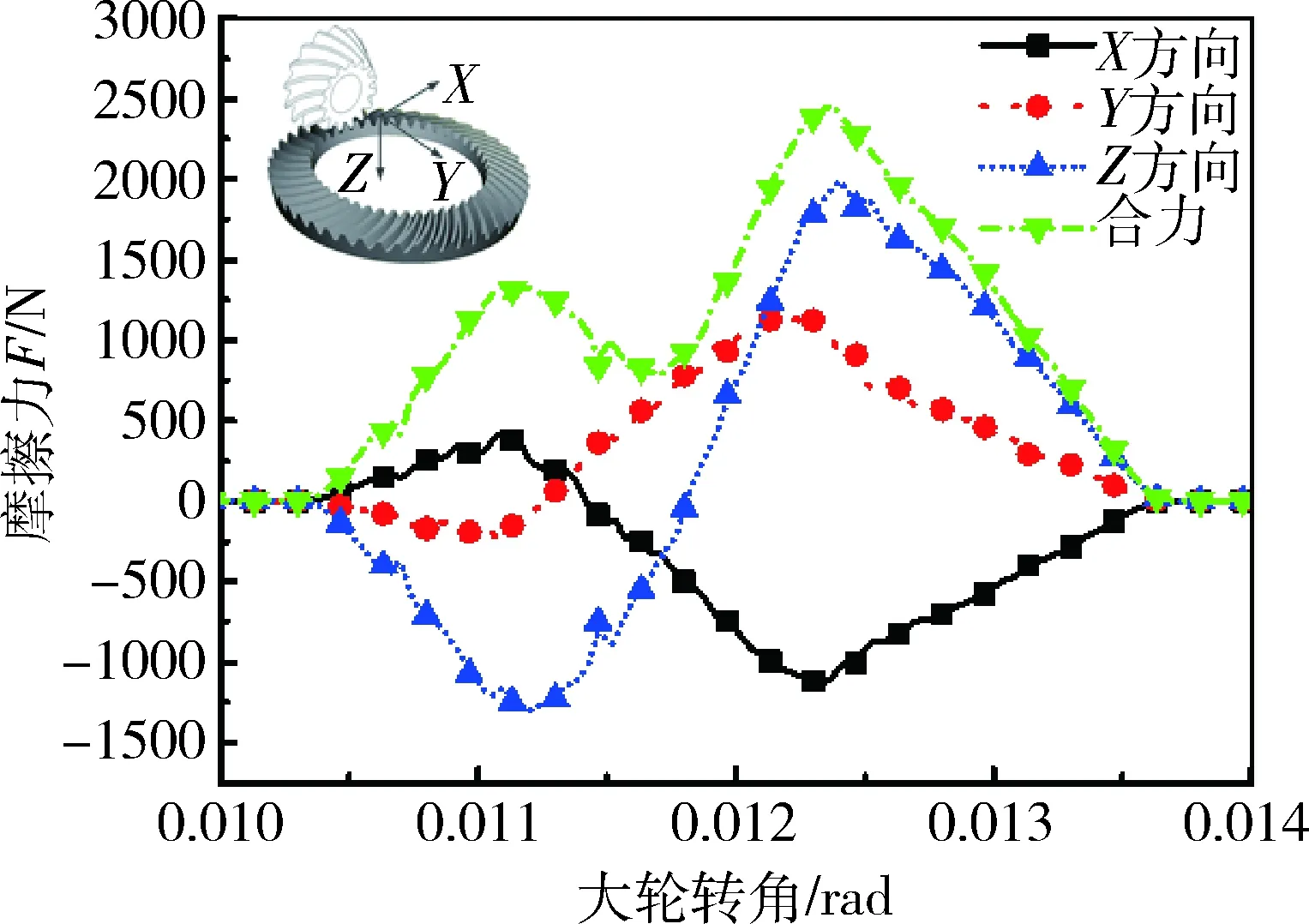
图8 各个方向摩擦力与总摩擦力变化Fig.8 Changes of friction in all directionsand total friction

4 结 论

1) 混合润滑模型求解摩擦系数呈现先增大后减小的趋势，摩擦系数经验公式计算结果在节锥母线附近误差较大，混合润滑模型求解结果更加可靠.

2) 研究混合润滑状态下不同啮合路径对齿轮动态传动误差的影响，结果显示大、小两端接触时传动误差偏大，中部接触时传动误差最小，传动更平稳.

3) 对比混合润滑状态不同啮合位置接触力及摩擦力变化，中部接触时接触中点附近润滑状况较好，摩擦损失少，接触性能更好，这对弧齿锥齿轮实际装配中啮合路径选择有一定的指导意义.