基于MPC的大型客车转向-制动集成控制研究＊

胡剑 刘鹏 李刚炎

（武汉理工大学，武汉 430070）

主题词：大型客车 转向-制动 集成控制 MPC

1 前言

大型客车因具有体积大、质量重、重心高、轮距相对较小等特点，在行驶过程中极易发生重大交通事故[1]。一些学者针对此问题进行了相关研究，如，文献[2]提出了基于行驶稳定性评价的主动前轮转向（Active Front Steering,AFS）和差动制动（Differential Braking Control,DBC）协调控制策略，并根据前轮转向角的大小来分配AFS和DBC的控制权重；文献[3]和文献[4]提出了基于横摆角速度和质心侧偏角的AFS和DBC协调控制策略，并采用模糊分配法对AFS和DBC的权重进行调节；文献[5]对AFS和DBC之间的耦合进行了分析，并利用线性2自由度车辆模型和PID控制器对其进行解耦和控制。这些研究大多是建立在单独的主动前轮转向系统和差动制动系统之上进行协调或解耦控制，并未实现完全的集成控制，不仅不能充分发挥AFS和DBC的各自功能，还可能导致整车性能降低，因此合理协调这些主动安全技术成为大型客车稳定性控制的关键。

基于此，本文建立了大型客车三自由度简化模型，确定了大型客车稳定性控制参数及其参考值，设计了大型客车转向-制动集成控制结构，并基于模型预测控制（Model Predictive Control,MPC）的集成控制策略，通过差动制动产生的附加横摆力矩以及主动前轮转向产生的附加前轮转角共同来控制大型客车的行驶稳定性。分别在双移线工况和正弦输入工况下，利用MATLAB/Simulink对大型客车转向-制动集成控制方法进行了仿真验证。

2 大型客车转向-制动集成控制结构

大型客车稳定性控制的关键之一是控制指标的选取。由于大型客车具有重心高、易侧翻的特点，所以将横摆角速度ωr[6]、侧倾角φ和质心侧偏角β共同作为大型客车稳定性控制指标。

采用分层模块化控制结构来实现大型客车转向-制动的集成控制，将其分为观测层、集成控制层和控制分配层3个层次，如图1所示。观测层通过接收车辆纵向速度Vx和前轮转角δ，利用参考模型得出参考横摆角速度、参考侧倾角和参考质心侧偏角，并与实际状态参数值进行比较，计算出横摆角速度偏差Δω、侧倾角偏差Δφ和质心侧偏角偏差Δβ；集成控制层利用模型预测控制算法，根据3个控制变量的偏差计算出附加前轮转角Δδ和附加横摆力矩ΔM。其中，附加前轮转角直接作用于被控车辆的主动前轮转向系统，附加的横摆力矩通过控制分配层转化为四轮制动力Fij作用于被控车辆的制动系统。利用这种分层模块化集成控制结构可有效消除差动制动系统和主动前轮转向系统之间的耦合。

图1 大型客车转向-制动集成控制结构

3 大型客车动力学模型

针对大型客车建立了含有横摆运动、侧向运动和侧倾运动的大型客车非线性三自由度模型，如图2所示。

图2 大型客车动力学模型

对大型客车进行受力分析，可得绕Z轴旋转、绕X轴旋转和沿Y轴方向运动的动力学方程：

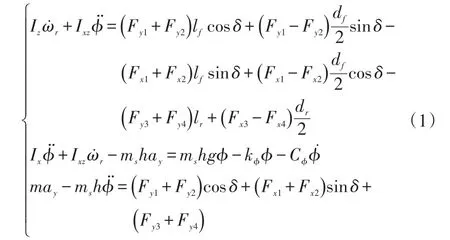
式中，ms为簧载质量；m为整车质量；Iz为绕Z轴旋转的转动惯量；Ix为绕X轴旋转的转动惯量；Ixz为绕XOZ平面旋转的转动惯量；ωr为横摆角速度；ay为侧向加速度；h为簧载质心到侧倾中心的高度；Fyi为各车轮所受侧向力；Fxi为各车轮所受的纵向力；φ为簧载车身侧倾角；lf为前轴距质心距离；lr为后轴距质心距离；df为前轴宽度；dr为后轴宽度；kφ为侧倾角刚度；Cφ为悬架阻尼。

轮胎的纵向力Fx和侧向力Fy利用“魔术公式”轮胎模型[7]（Magic Formula Tire Model）进行计算：

式中，a为轮胎侧偏角；μ为路面附着系数；Fz为轮胎垂向力；s为轮胎滑移率；Bx、Cx、Dx、By、Cy、Dy为常数。

前轮轮胎侧偏角ai和后轮胎侧偏角aj计算式为：

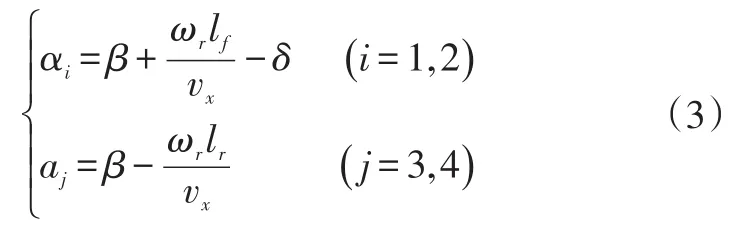
前轮轮胎垂向载荷Fzi和后轮轮胎垂向载荷Fzj计算式为：

式中，hg为侧倾中心高度；l为前轴距后轴距离；Kφf为前轴侧倾角刚度；Kφr为后轴侧倾角刚度。

“魔术公式”轮胎模型所表示的是单一方向轮胎力计算模型，由于“摩擦椭圆”[8]的限制，轮胎所受的纵向力和侧向力相互影响，可根据文献[7]所推荐方法对联合工况轮胎力进行修正。

4 大型客车转向-制动集成控制器设计

大型客车转向-制动集成控制器设计主要包括参考模型的确定、MPC控制器的设计和附加横摆力矩分配控制器的设计。

4.1 参考模型建立

以常用的线性2自由度大型客车动力学模型作为参考模型，为集成控制器提供质心侧偏角的参考值和横摆角速度的参考值，如图3所示。式中，β2为2自由度下的大型客车质心侧偏角；ωr2为2自由度下的大型客车横摆角速度；kr为后轮侧偏刚度；kf为前轮侧偏刚度。

图3 参考模型

式中，K为稳定性因子，可由轮胎侧偏刚度和车辆轴距求得。

受限于路面附着系数，最大质心侧偏角βmax和最大横摆角速度ωmax计算式为：

当参考模型计算的参考值超过实际工况最大限制值时，应由最大质心侧偏角βmax和最大横摆角速度ωmax作为实际参考值，即ωref=min(ωref2,ωmax)，βref=min(βref2,βmax)。为防止大型客车的侧翻，将车辆侧倾角的参考值φref取为0。

4.2MPC控制器设计

MPC是一种在工业中被广泛应用的先进控制方法，它利用预测模型，根据被控系统的过程状态信息进行判断，从而实现滚动优化和反馈矫正，具有鲁棒性强、在线实时性好等优点[9]。

为方便建立大型客车转向-制动集成控制中MPC控制器的预测模型，采用局部线性化的思想将复杂的非线性轮胎模型线性化，即：

式中，Fyf为前轮轮胎侧向力，Fyr为后轮轮胎侧向力，af为前轮轮胎侧偏角，ar为后轮轮胎侧偏角。

根据式（1）和式（8），加入附加前轮转角和附加横摆力矩的大型客车动力学模型状态空间表达式为：

将其写成预测模型的形式：

式中，O=为控制变量的系数矩阵；u(k)=为控制变量；d(δ)=Nδ为固定项；B=为状态变量到输出变量的系数矩阵；Y(k)为输出变量。

将上述预测模型离散化，并变换成增量的表达形式。根据变换后的预测模型，可得控制输出量的预测序列，用矩阵形式表达为：

式中，Yp为输出量的预测序列，ΔU为控制量增量，F为输出量的预测序列的系数矩阵，K为控制量增量的系数矩阵。

为保证控制效果，MPC控制器性能指标设计为：

式中，Q为目标跟踪误差的权重；R为控制量变化大小的权重。

另外，在控制过程中系统控制量和状态量需要满足下述约束：

4.3 附加横摆力矩分配控制器设计

通过模型预测算法得到附加横摆力矩后，需要对大型客车的各车轮施加不同的制动力。目前比较成熟的附加横摆力矩分配算法有广义逆法、直接分配法、链式递增法及数学规划法等。本文选取单轮制动直接分配法，其具有结构与算法简单、实时性强、易于实现且成本较低等优点。

对车轮进行受力分析，得到单轮制动所产生的横摆力矩为：

大型客车的转弯特性可分为中性转向、转向过度和转向不足[10]。当横摆角速度的实际值大于参考值时属于转向过度，此时对大型客车外前轮进行制动以产生与大型客车转向相反的附加横摆力矩，抑制其过度转向；当横摆角速度的实际值小于参考值时属于转向不足，此时对大型客车内后轮进行制动以产生与大型客车转向相同的附加横摆力矩，抑制其转向不足。附加的横摆力矩分配策略如表1所示。

表1 附加横摆力矩分配策略

5 仿真验证

为验证所设计的模型和集成控制器的可行性和有效性，采用MATLAB/Simulink搭建大型客车动力学模型和集成控制器模型，分别在双移线工况和正弦输入工况下进行了仿真研究，仿真验证模型如图4所示。

图4 大型客车转向-制动集成控制Simulink仿真模型

经过反复调试，所设计的MPC集成控制器参数如下：

a. 采样周期为0.01 s，控制时域为3，预测时域为15。

b. 权重矩阵Q：Q11=100，Q22=500，Q33=120，当i≠j时，Qij=0；

c. 权重矩阵R：R11=2，R22=0.01，当i≠j时，Rij=0。

d.约束条件如下：

附加横摆力矩边界约束：-500～500 N∙m；

附加横摆力矩增量约束：-40～40 N∙m；

附加前轮转角边界约束：-0.1～0.1 rad；

附加前轮转角增量约束：-0.03～0.03 rad；

侧倾角约束：-0.12～0.12 rad；

质心侧偏角约束：-0.09～0.09 rad；

横摆角速度约束：-0.35～0.35 rad/s。

5.1 双移线工况仿真

双移线转向输入是模拟驾驶员急速超车的工况，是车辆操纵稳定性和行驶稳定性测试的常用工况之一。根据标准ISO 3888-1-1999《乘用车-急剧换道用车道第1部分：两车道变换》有关规定，设置双移线工况下的转向盘转角如图5所示，设置大型客车的初始速度Vx=72 km/h，路面附着系数μ=0.85，仿真结果如图6所示。

图5 双移线工况下的转向盘转角

图6 双移线工况下集成控制仿真结果

5.2 正弦输入工况仿真

正弦输入工况下的转向盘转角如图7所示。设置大型客车的初始速度Vx=72 km/h，路面附着系数μ=0.85，仿真结果如图8所示。

图7 正弦输入工况下的转向盘转角

图8 正弦输入工况下集成控制仿真结果

通过对所设计的大型客车转向-制动集成控制仿真分析可知，与没有集成控制的大型客车相比，本文所设计的模型预测控制器能有效跟踪控制指标的参考值，保证了车辆的行驶稳定性。

6 结束语

本文提出了一种基于模型预测控制（MPC）的大型客车转向-制动集成控制算法，并分别在双移线工况和正弦输入工况下进行了仿真验证，结果表明，与没有集成控制的大型客车相比，基于模型预测策略所设计的大型客车转向-制动集成控制器能同时控制车辆横摆角速度、侧倾角和质心侧偏角，可有效跟踪控制指标的参考值，保证了大型客车的行驶稳定性。