基于视觉和车辆动力学的库位跟踪算法研究＊

余卓平 许明煜 张培志 熊璐 黄禹尧

（同济大学，上海 201804）

主题词：自主泊车 车辆动力学 定位 库位跟踪 扩展卡尔曼滤波

1 前言

自动泊车系统的应用可以提高交通效率和安全性，具有广阔的市场前景[1]。在国内市场，自动泊车系统搭载范围逐渐从高档轿车延伸到中档轿车中。

定位与库位跟踪作为自动泊车环境感知技术的一部分，是后续规划和控制的基础。目前智能驾驶技术常用的环境感知传感器有差分GPS接收器、惯性导航系统、相机和激光雷达等，选择虽然很多，但每种传感器对于自动泊车来说优、缺点都十分明显。差分GPS接收器成本高昂，且在室内或有建筑物遮挡的区域信号缺失严重；高精度惯导设备同样成本高昂，且难以避免长时间运行时的数据漂移现象；相机获取的数据丰富，但易受环境光线等因素影响，且图像处理算法对计算资源要求较高；激光雷达的优点是精度高、测量范围广，缺点是成本高昂、数据信息不够丰富，且目前没有成熟的车载级产品。基于以上传感器的特点，相机成为目前自动泊车技术最主流的传感器[2]。

环视鱼眼相机由于其成本低廉、视野范围广等优点被广泛使用。在自动泊车中，环视相机主要被用于检测库位线及获得库位的相对位置。受光线等因素影响，现有库位检测算法鲁棒性较差，不能在整个泊车过程中持续跟踪库位[3]；又由于鱼眼相机在视野边缘存在较大畸变，库位检测的结果往往有较大误差[4]。

在自动泊车中，车辆定位主要依靠航位推算。航位推算信号来源为车辆底盘控制数据，包括轮速传感器数据和转向盘转角。普通航位推算算法基于阿克曼转角模型推导。虽然自动泊车过程速度较低，但仍然存在一定的质心侧偏角，只适用于准静态工况的阿克曼转角模型不能满足泊车定位精度的需求。由于车辆底盘数据噪声的存在，航位推算的累积误差也会使泊车过程后期出现定位漂移。

针对上述问题，本文设计了一种融合车辆底盘数据和环视相机数据的库位跟踪算法，可以在泊车过程中实时估计车辆位姿并跟踪库位角点，为后续再规划提供更精确的环境信息。

2 库位跟踪算法

2.1 算法基本架构

库位跟踪的本质是状态估计问题。将车辆位姿和库位角点坐标视为服从某种概率分布的随机变量，在常见情况下，假设状态变量和噪声项均服从高斯分布，于是问题可以描述成：在已知车辆底盘运动数据和环视观测数据时，如何确定状态变量的概率分布。由于泊车环境对实时性要求较高，且环境中库位角点数量有限，将路标坐标也加入状态变量，采用紧耦合的高斯滤波方法来融合两种数据。又由于运动过程和观测过程为非线性，使用扩展卡尔曼滤波（Extended Kalman Filter，EKF）进行库位跟踪[5]，算法流程如图1所示。

2.2 车辆动力学模型

为了对车辆的动力学特性进行分析，并以此为基础设计相应的航位推算算法，需要建立正确、有效的车辆动力学模型。二自由度单轨模型以质心侧偏角和横摆角速度作为系统的状态变量，如图2所示。建模时需作如下简化：假设整车质量集中于质心处；轮胎与地面的附着力通过前、后车轮直接传递；忽略悬架的作用；认为汽车平行于地面运动，即汽车垂向位移、俯仰角和侧倾角均为零。由牛顿第二定律可以得到等效动力学方程：

式中，β、ψ分别为质心侧偏角和横摆角；Ff、Fr分别为前、后轴侧向力；lf、lr分别为质心到前、后轴的距离；δ为前轮转角；J为车辆质心处绕z轴的转动惯量；v为质心处的速度。

采用线性模型描述轮胎侧偏角与侧向力的关系：

式中，Fy、α分别为轮胎的侧向力和侧偏角；k为轮胎侧偏刚度。

前、后轮侧偏角分别为：

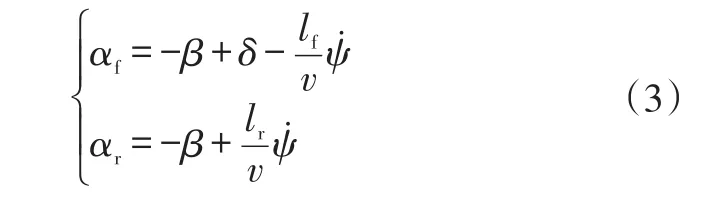
结合式（1）～式（3），可以得到以前轮转角和质心速度为输入、以质心侧偏角速度和横摆角加速度为状态变量的方程组：

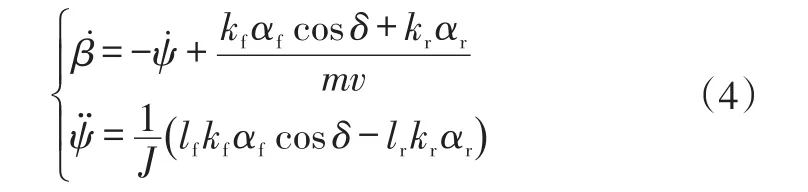
式中，kf为前轮轮胎侧偏刚度；kr为后轮轮胎侧偏刚度。

本文以车辆二自由度模型为基础进行质心侧偏角和横摆角速度估计算法的设计。采用线性轮胎模型的车辆质心侧偏角估计方法在极限工况时误差较大[6]，但自主泊车一般在低速小激励工况下进行，考虑到即便在低速工况下，质心侧偏角仍然存在，而基于阿克曼转角的纯几何模型完全不考虑质心侧偏角的影响，因此轮胎刚度为线性的二自由度车辆模型可以满足航位推算精度要求[7]。

2.3 环视库位检测及图像拼接

系统从车载的4个鱼眼相机中实时获取图像并对其进行拼接。通过机器学习算法，可以从获得的鸟瞰视图中检测到相应的库位点，经过相似变换计算获得库位点相对于车辆的二维平面坐标，并实时地发送给决策系统，如图3所示。

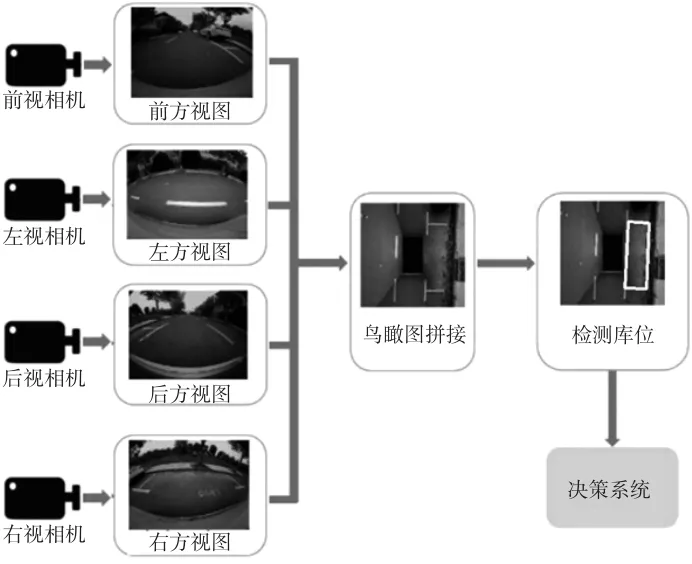
图3 基于环视视觉的泊车库位检测系统整体流程

环视系统鸟瞰图由前、后、左、右4个环视图像分别进行坐标变换后拼接而成。4个相机的视角均为180°，因此可以围成除车身内部外的无盲区视野范围。由于经历了多次坐标变换，如图4所示，可建立反向查找表以提高算法执行的效率。针对鸟瞰图中的每个像素点，通过一个相似矩阵计算其对应的车身固结坐标系中的位置坐标，再通过一组仿射变换矩阵计算对应世界坐标系中的点对应到去畸变图像中的坐标，最终通过畸变多项式模型计算其所对应的原始图像像素的位置，取得该像素的颜色。

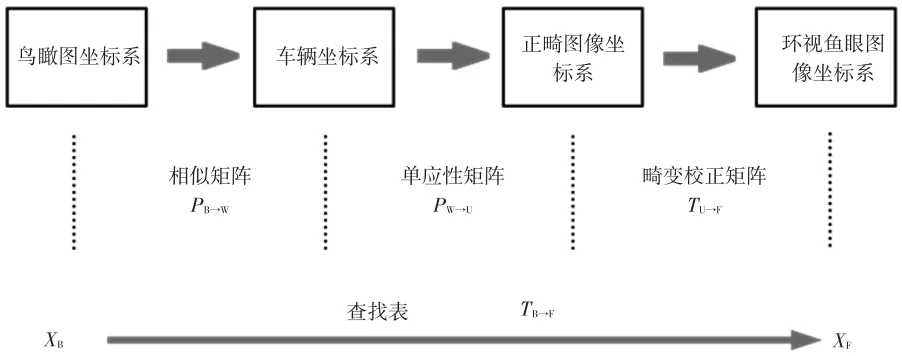
图4 从鸟瞰图到鱼眼图像的坐标变换

从鸟瞰图到车辆坐标系的变换为相似变换，其参数可以由鸟瞰图的像素范围及其对应的地面视野物理尺寸事先算得；在虚拟场景中，可以使用无畸变的相机从鸟瞰视角拍摄一个场景作为成像拼接的参考，则可以非常容易地计算得到比例系数。

从车辆坐标系到单个鱼眼镜头去畸变后的图像的变换，需采用单应矩阵，手工选择4组对应点即可完成相应变换。需要注意的是，此处所指的车辆坐标系原点在车辆质心处，为车身固结坐标系，在标定时车辆静止，仅在此时可认为与大地坐标系相重合。

从去畸变后的图像到相机所成原始图像之间则依靠多项式桶形畸变模型联系在一起。上述步骤均可以查找表的形式保存下来，以便拼接时实时使用。

2.4 基于扩展卡尔曼滤波的数据融合

扩展卡尔曼滤波算法采用的世界坐标系和基本状态变量定义如图5所示，定义世界坐标系原点为泊车初始时刻车辆质心位置。

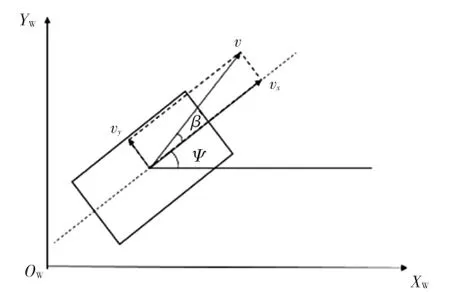
图5 EKF算法的坐标系和状态量定义

2.4.1 运动方程

根据车身位姿估计和库位跟踪的目标，构建状态变量的运动方程：

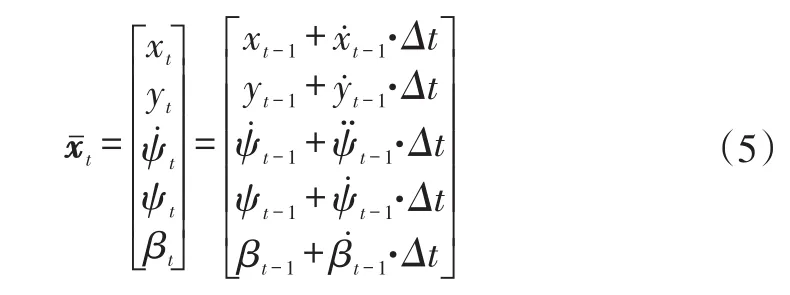
式中，为根据运动方程预测得到的t时刻状态先验值；xt和yt为t时刻世界坐标系下车辆位移。

根据运动学旋转关系，有：

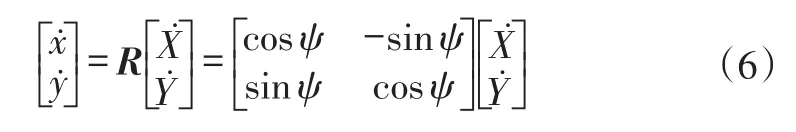
式中，X、Y为车辆坐标系下的位移；R为二维平面车辆坐标系相对于世界坐标系的旋转矩阵。

根据质心侧偏角的定义，有：

根据式（3）和式（4），可以将横摆角加速度表达为：

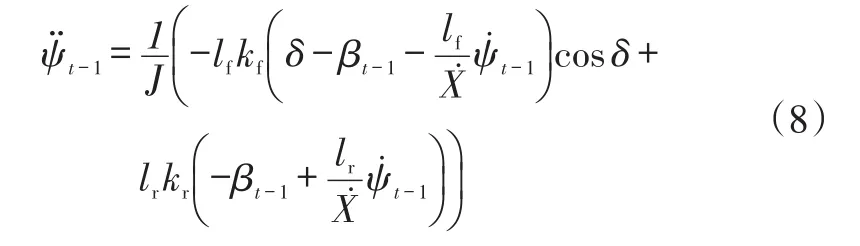
同理，根据式（3）和式（4），质心侧偏角速度可以表示为：

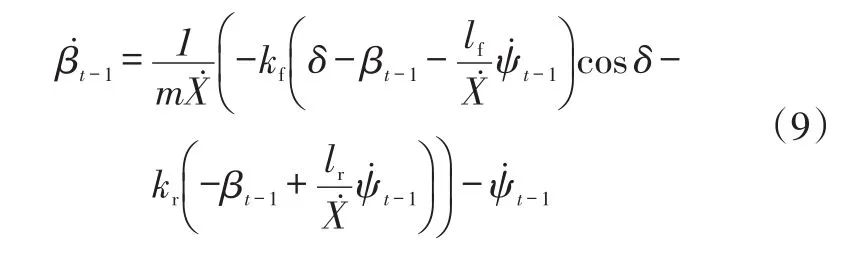
2.4.2 观测方程

库位角点检测结果为车辆坐标系下库位角点的坐标，直接用作观测变量会导致将状态变量映射到观测变量的观测方程形式复杂，同时提高后续求导步骤的难度，需要增加额外的计算资源。因此，预先将通过图像处理算法计算得到的观测数据进行数学处理（库位角点与车辆坐标系的几何关系见图6），得到库位角点相对于车辆的距离和方向：

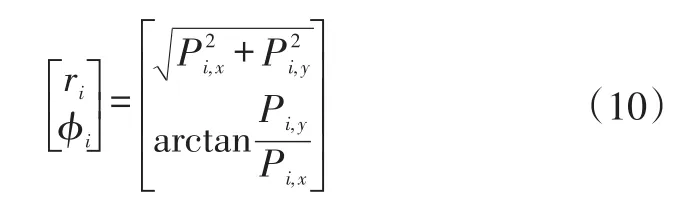
式中，Pi,x、Pi,y分别为第i个库位角点在车辆坐标系下的x、y坐标；φi为第i个库位角点与车辆坐标系x轴的夹角。

图6 库位观测示意

选取库位角点相对车辆的距离和方向为观测变量，根据图6所示的几何关系，可以确定观测方程的形式：

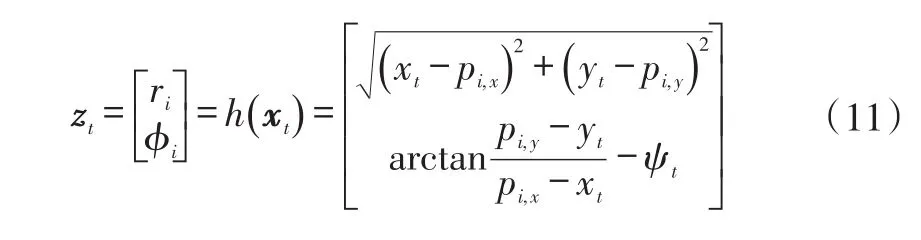
式中，zt、xt分别为t时刻观测变量和状态变量；pi,x、pi,y为对应时刻检测到的库位角点在世界坐标系下的坐标。

2.4.3 预测过程协方差矩阵传播

由于运动方程是关于(t-1)时刻状态变量xt-1的非线性函数，要知道从(t-1)时刻到t时刻系统状态协方差矩阵的传播，首先需求得运动函数关于xt-1的Jacobian矩阵：

式中，Ft为t时刻的运动Jacobian矩阵；f为运动过程函数。

Jacobian矩阵中各偏导具体表达式为：

得到Jacobian矩阵表达式后，(t-1)时刻到t时刻运动过程的协方差矩阵可以由下式更新：

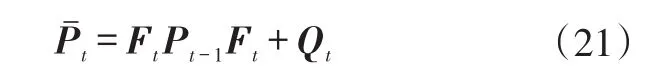
式中，为状态协方差先验值；Pt-1为(t-1)时刻状态协方差矩阵；Qt为运动噪声协方差。

2.4.4 观测更新

考虑到观测方程也是关于车辆状态变量xt的非线性函数，进行观测更新时同样需要计算观测函数关于xt的Jacobian矩阵，将新观测到的库位角点世界坐标系坐标作为优化变量增广到状态变量中：

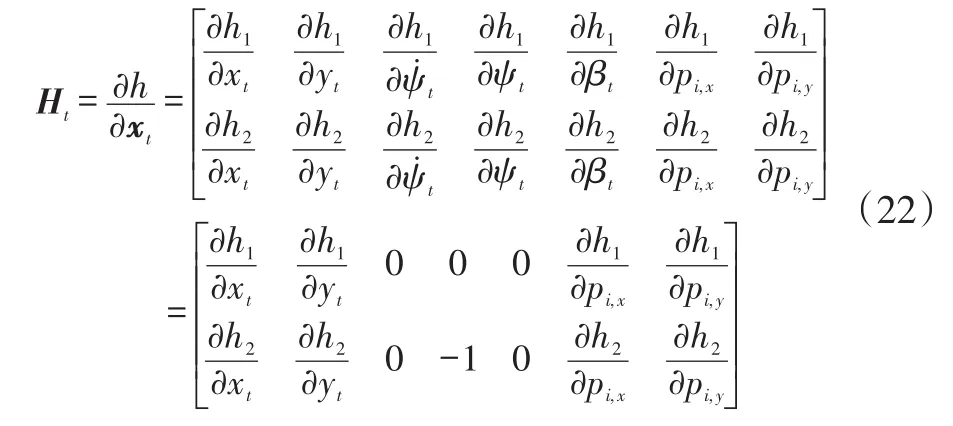
式中，Ht为t时刻的观测Jacobian矩阵；h为观测函数。

Jacobian矩阵中各偏导具体表达式为：

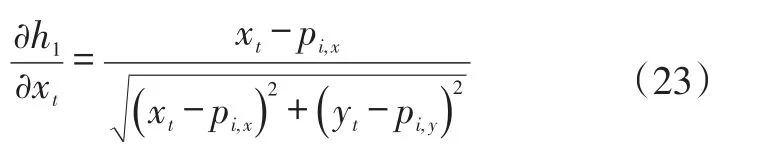
至此，可以计算卡尔曼增益：

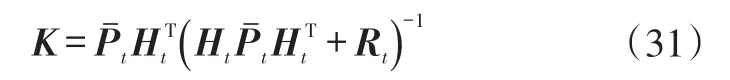
式中，Rt为观测噪声协方差。

获得卡尔曼增益后，可以更新状态变量的后验估计：

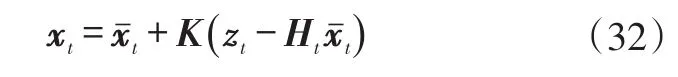
式中，zt为t时刻观测变量。

同时更新状态变量后验协方差：

2.4.5 数据关联

考虑到每帧环视图像视野内的库位角点数量不多，使用欧式距离即可满足数据关联的要求。如果环视图像视野内检测到1个库位角点，则将该库位角点与已有路标信息进行匹配，匹配方法为：若与系统状态中已有路标的欧式距离不小于某一阈值，则认为该库位点是新路标，此时对系统的状态进行增广；若小于某一阈值，则利用EKF算法进行更新。

3 仿真与试验

3.1 仿真验证

本文仿真环境基于MATLAB和PreScan搭建，泊车场景如图7所示。

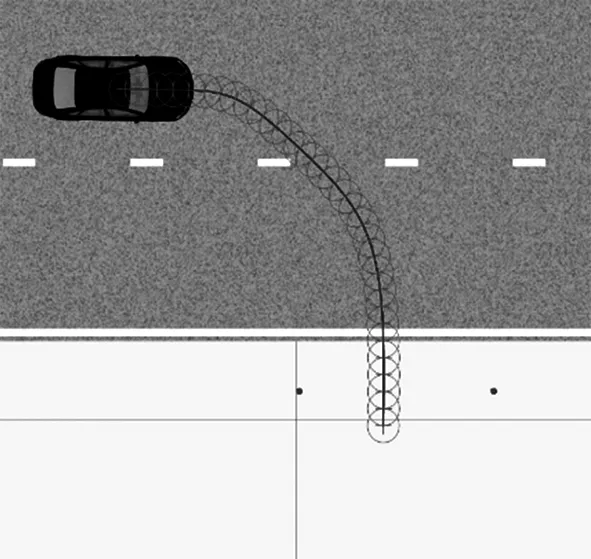
图7 仿真场景

场景设置了2个库位角点，由车载传感器可以获得角点相对于车辆的距离和角度，仿真中加入高斯噪声以模拟在光照等因素的影响下环视相机检测获得的库位角点坐标[8]。车辆按照预先设定的路径进入车位，记录运动过程中库位位置、纯航位推算轨迹、融合轨迹和真实轨迹。航位推算轨迹与真实轨迹对比结果如图8所示，融合轨迹与真实轨迹对比结果如图9所示。

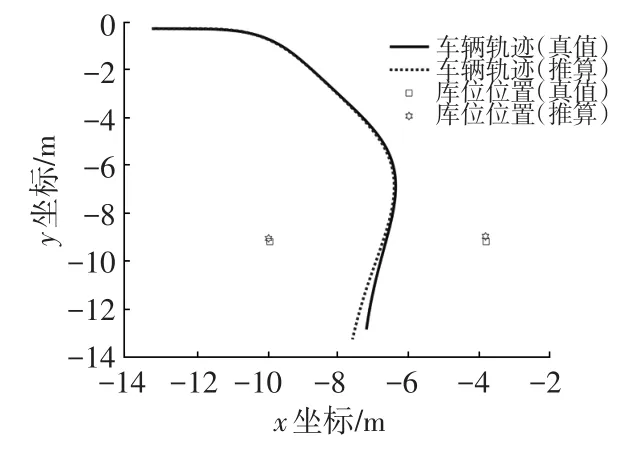
图8 纯航位推算定位仿真结果

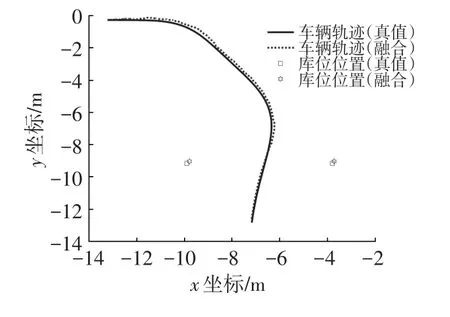
图9 融合库位检测结果的组合定位仿真结果

由仿真结果可知，整个泊车过程行驶总距离12.5 m，纯航位推算定位累积误差约为0.4 m，且误差有逐渐增大的趋势，而融合库位检测后的结果最大误差在0.3 m以下，且累积误差逐渐收敛趋于零。

3.2 实车试验

实车试验平台为荣威E50电动车，车上装有工控机、环视相机和差分GPS接收器。试验过程中采集的数据有车辆轮速、转向盘转角、环视相机图像和差分GPS定位数据，由于差分GPS定位精度在10 cm以内，认为其数据为真值。试验平台和泊车过程分别如图10、图11所示。

图10 实车试验平台

图11 泊车过程

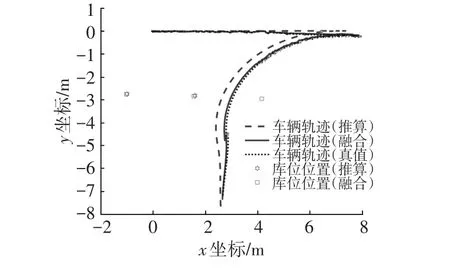
图12 一次泊车入库试验结果

图13 二次泊车入库试验结果

试验中分别采用一次泊入和二次泊入的方式完成泊车，记录的结果分别如图12、图13所示。由实车试验结果可知，纯航位推算结果在泊车过程中最大误差约为0.6 m，而融合库位检测后的结果最大误差约为0.2 m，且整个过程的趋势与车辆轨迹真值更加接近，说明本文提出的算法能准确估计泊车过程中的车辆位姿，有效降低航位推算累积误差。

4 结束语

本文基于车辆动力学模型，利用扩展卡尔曼滤波融合航位推算和库位检测结果设计了一种泊车定位及库位跟踪算法。仿真和实车试验结果表明，该方法可以有效降低航位推算累积误差，实时估计车辆位姿，并在整个泊车过程中持续跟踪库位角点，为自动泊车后续过程提供更准确的环境信息。

另外，本文在状态估计中采用了扩展卡尔曼滤波方法，而无迹卡尔曼滤波、粒子滤波、非线性优化等常用的状态估计方法[9]在实时性、优化效率、估计精度等指标上的效果值得进一步研究。