圆锥曲线核心考点测试卷A 参考答案

一、选择题

1.B 2.C 3.A 4.B 5.D 6.A

7.B 8.B 9.C 10.A 11.A 12.C

二、填空题

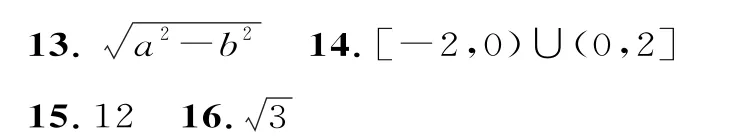
三、解答题

17.如图1所示,以A为坐标原点,A B所在直线为x轴,建立平面直角坐标系。

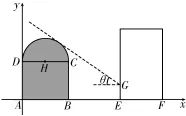
图1

(1)因为A B=18,A D=6,所以半圆的圆心为H(9,6),半径r=9。设太阳光线所在直线方程为,即3x+4y-,解得b=24或故太阳光线所在直线方程为得E G=1.5＜2.5。所以此时能保证上述采光要求。

(2)设A D=hm,A B=2rm,则半圆的圆心为H(r,h),半径为r。

欲使活动中心内部空间尽可能大,则影长E G恰为2.5m,则此时点G为(30,2.5)。

设过点G的上述太阳光线为l1,则l1所在直线方程为4y-100=0。由直线l1与半圆H相切,得

而点H(r,h)在直线l1的下方,则3r+4h-100＜0,即,从而

所以当A B=2 0m且A D=5m时,可使得活动中心的截面面积最大。

18.(1)以C为原点,L所在的直线为x轴建立直角坐标系,如图2所示,则B(-69)。

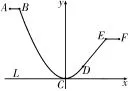
图2

设抛物线的方程为y=a x2,将点B(-6,9)代入y=a x2,得,故抛物线方程为

故D点的坐标是(2,1)。

(2)设所求圆的圆心为H。过D与L垂直的直线方程是l1:y=-x+3,B D的中点坐标是(-2,5),kBD=-1,故B D的中垂线方程是y=x+7。

由于H是B D的中点,所以H(-2,5)。因为B(-6,9)∈l1,所以B D是直径。

因为圆心H到L的距离为d=55＜42=r,故圆弧与地平线L相交。

19.(1)抛物线C2的焦点坐标为(0,,所以椭圆的一个顶点为,即b=所以

(2)由题意,直线l与椭圆必相交。

②斜率存在时,设方程为y=k(x-1)(k≠0),M(x1,y1),N(x2,y2)。将直线方程代入椭圆方程,消去y得(3+4k2)x2-8k2x+4k2-12=0,所以故直线l的方程为y=

设H(a,-1),所以D(a,0)。

(2)直线E T与抛物线相切,理由如下:

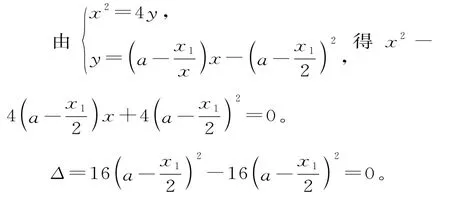
所以直线E T与抛物线相切。

又c=1,所以a2=b2+c2=5,所以椭圆C的方程为

设A(x1,y1),B(x2,y2),则x1+x2=O到直线A B的距离

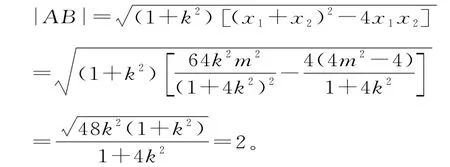
所以4k4-4k2+1=0,解得所以直线A B的方程