基于实时识别焦虑情绪的音乐重构

沙文青，郭滨，王宏旭，白雪梅，张晨洁

（长春理工大学 电子信息工程学院，长春 130022）

近年来，随着社会的发展，人们的生活节奏越来越快，许多人都会产生负面情绪，焦虑就是较典型的负面状态之一，长期处于焦虑状态会对自身的健康产生严重的影响。音乐疗法作为缓解负面情绪的有效工具，被人们广泛接受。但是传统的音乐疗法存在以下几个问题：一是对患者的情绪定位不明确；二是不同的人对同一首音乐会有不同的感受，音乐治疗师很难准确把握每一个人的情感反馈；三是由于乐曲多而杂，在有限的时间里，治疗师很难简化乐曲的同时提高改善效果。研究人员尝试使用生物反馈技术，如脑电图（EEG）来衡量音乐治疗的效果，因为它能敏感地、客观地反映人们的情绪。

Vangu Kitoko等人发现高压受试者的β水平活动增加[6]；Leiden University等人发现SW/FW（慢波/快波）与焦虑呈负相关[8]；Bos利用傅里叶变换得到脑电信号在不同频段的能量比可以作为表征情绪的特征[10]。卢英俊、戴丽丽等人发现通过分析α频段的脑电功率和重心功率表明在中国古典音乐、中国摇滚音乐、中国流行音乐和班得瑞音乐的音乐干预下，中国古典音乐最能缓解悲伤情绪，中国摇滚乐缓解效果最差[1]；付丹等人选择了120名患有轻度焦虑症的大一新生为研究对象，随机分为音乐治疗组合和音乐治疗结合生物反馈组，八周治疗后发现音乐治疗结合生物反馈组更能缓解焦虑情绪[2]；Syed Syahril等人研究发现可以使用α峰值频率来量化个体所经历的快乐程度[4]。

本研究设计实验获得焦虑情绪的脑电信号，通过分析beta与alpha的单位时间内的功率比的波动变化来量化焦虑情绪，探究实时区分焦虑状态和平静状态的条件进行焦虑情绪的识别。

1 情绪识别理论分析及实验方法

1.1 情绪识别理论分析

EEG信号是一种随机性很强的非平稳微弱信号，极易受到各种噪声的干扰，比如工频干扰、眼电等，为了让提取的特征更加准确，在特征提取之前要对脑电信号进行预处理，即去噪。希尔伯特-黄变换（HHT）中的经验模态分解（EMD）方法可以根据信号的实际情况，自适应地分解信号。Fast ICA能够较快的收敛于最佳分解状态，所以可以将两种方法相结合，引入到脑电信号的去伪迹的研究中。数据预处理之后，可以得到比较纯净的脑电信号。

根据频率范围，脑电波被分为如下：β波（13～35Hz）、α波（8～13Hz）、θ波（4～8Hz）和δ波（0.16～4Hz），脑电信号在不同频带上表现出的不同特征可以用来判断一个人的精神状态特征。α波与人们的放松有关，高阿尔法活动与低脑活动有关。β波是一种高频脑波，主要与心理警戒状态相关，即测量β/α波可以反映人们的情绪，当比值降低时，人们处于消极负面的情绪状态，当比值升高时，人们处于较活跃的状态。

设计切比雪夫滤波器提取脑电信号的四种节律，即利用kaiserord函数获取滤波器参数，然后在N+1阶kaiser窗口下使用fir带通滤波器进行滤波，得到脑电信号的四种节律。

1.2 焦虑情绪诱导实验设计

本文采取情景设计诱导情绪的实验方法，具体是选择10名被试者，年龄均为19-24周岁，其中5名为男性，5名女性。被试者身体健康，视力正常，无神经性疾病历史，并在实验前一周未服用过任何药物。设计一个英语课堂，被试者需佩戴便携式3IT_EHV1脑电帽坐在一间教室里，老师在上课期间会对被试者提出不同的问题。由被试者回答，并且老师根据回答内容给出评分，被试者通常会因此出现焦虑的情绪，最终分数最低的人需要表演一个节目，这是为了增强被试者回答问题前的焦虑感。课堂结束之后，会对十位被试人员询问上课过程中情绪的变化，尤其是在老师提出问题之后，被试者心理状态的变化。脑电信号由便携式脑电帽来采集，该设备是由8通道OpenBCI_V3脑电板以及配套的GUI数据分析软件组成。如图1所示，深色点和灰色点都为脑电采集点，深色为本设备选择的采集点。

图1 OpenBCI 8通道（①、②、③、④、⑤、⑥、⑦、⑧通道分别为Fp1、Fp2、C3、C4、P7、P8、O1、O2）

1.3 结果分析

有关研究表明大脑右额叶脑区与情绪状态之间的相互作用比较明显，因此选择Fp2通道的脑电信号进行去躁和脑电节律提取，滤波结果示例如图2所示。提取节律之后，根据公式计算alpha波和beta波单位时间内的功率，并计算两者之间的功率比，观察功率比的波动变化。

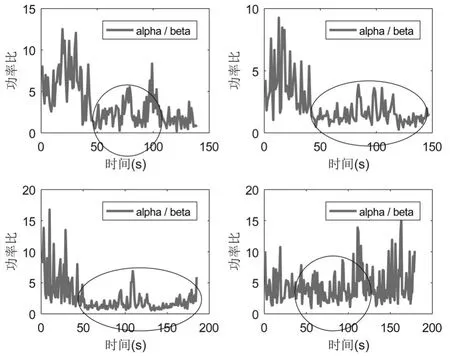
图2 其中四位被试者的alpha波和beta波功率比

对脑电信号进行分析之后，发现被试人员在老师提出问题之后的alpha波与beta波的功率比均出现不同程度的降低，如图3所示（椭圆部分比值降低），从对被试者后续调查可知，被试者表示在老师提出问题之后均出现了不同程度的焦虑情绪，由此看出，焦虑情绪会使alpha波与beta波的功率比降低，即alpha波与beta波的单位时间功率比的变化可以作为实时判决焦虑状态的依据。分析被试者脑电的alpha和beta功率比，探究识别焦虑情绪的阈值范围如表1所示。

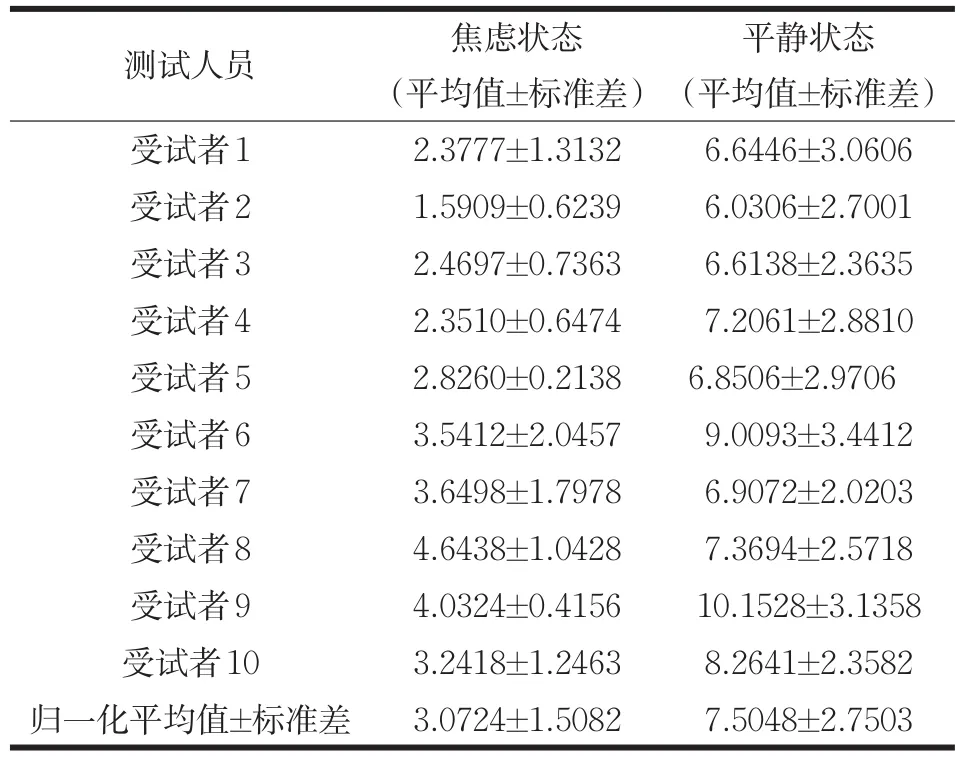
表1 平静状态和焦虑状态alpha和beta功率之比

根据表1中所示每个状态获得的归一化平均值确定分辨平静和焦虑状态功率比的阈值范围。如表2所示。

表2 阈值范围

2 音乐库的构建与音乐重构

上一章节得出识别焦虑状态和平静状态下的alpha波和beta波功率比的阈值范围。本章节设计实验对焦虑情绪进行改善，然后基于脑电波变化反馈提取对被试者有效的音乐片段，然后根据音乐作曲的基本理论知识和相关算法对音乐片段进行重新组合，创作新的音乐。

2.1 音乐分类原理

2.1.1 音乐特征提取

虽然音乐信号是一种长时非平稳时变信号，但在很短的时间内可以看作是平稳的、时不变的信号，所以在音乐信号进行处理前必须进行分帧[13]，即对音乐信号进行加窗处理。由于要对音乐片段进行实时分类，所以分类算法的计算不能很复杂，特征向量不能过多，所以选用相对容易的时域特征进行特征向量的选择。帧能量谱排列的紧密程度可以区分出音乐的节奏快慢，帧能量谱可以区分出音乐节奏的强弱[12]。所以本文采用帧能量（FE）和帧能量比（FER）两个特征向量来进行实时的音乐分类。

（1）帧能量

帧能量特征反应了音乐信号所含能量随时间变化的进程，而音乐信号的能量随时间的变化程度比较明显。离散后的音乐信号x(n)的第i帧能量FE(i)定义为：

式中，winlen是一帧的长度

（2）帧能量比

帧能量比表示相邻两帧之间的帧能量的比值，同时也是重要的短时时域特征，它能够反映音乐信号能量的起伏变化。FER(i)的计算公式为：

其中，FEi和FEi+1均不能为零。

2.1.2 音乐分类

BP（Back Propagation）神经网络是典型的多层网络，由神经元构成。它分为输入层、隐藏层和输出层。由于神经网络训练要求数量精炼，所以使用帧能量和帧能量比为实验特征进行训练。训练BP神经网络时则使用MATLAB自带神经网络工具箱中的BP网络的构建函数newff、训练算法则使用了学习率可变的动量BP算法（traingdx）、学习函数使用learngdm。

2.2 音乐重构原理

算法作曲（Algorithmic Composition）或称自动作曲（Automated Composition）是为了按照一定的规则将多个音乐片段组成一个有机整体的一系列的规则集合[23]。算法作曲并不一定需要利用计算机来创作，有关研究发现，莫扎特曾经运用过随机组合的方式来进行音乐模块创作“Musical Dice Game”，并取得了比较好的效果。因此本文首先对所保存的音乐片段按照风格进行分类，其次在每个类别中，利用马尔可夫链学习音乐片段，构建以音符为状态空间的马尔可夫模型，来组合音乐片段，创造新的音乐。

马尔可夫链是一个非确定性状态机，系统处于某种特定状态的概率仅取决于其以前的状态以及这些状态之间转换的概率。

音乐在时间上的变化通过音符体现，这主要表现在音符的音高和时值的变化，可以把这种变化看作是旋律随时间的运动，从一个音符状态运动到另一个音符状态，即可以通过状态转换表来描述。实验表明，通过计算和利用音符转换的概率，可以创建听起来像给定样式的音乐片段。更确切地说，给定一组音乐素材（通常是乐谱或MIDI文件）可以计算连续音符之间的转换概率。通过使用这些概率分布生成音符，产生新的音乐。本文通过学习音乐片段，生成状态转换表，得出组合音乐片段的最佳顺序。

音符具有两种基本属性：音高和时值，音符状态的变化包括音符音高状态的变化和音符时值状态的变化。在五线谱中，音符是一个黑色椭圆形的记号，它写在哪一条线（或间）上，就表示应该发出那一条线（或间）的音高。为了表示音符发音时间的长短即时值，音符有几种不同的形状，常见的有五种：全音符、二分音符、四分音符、八分音符、十六分音符。

隐马尔可夫模型是一种时域上的统计模型，在HMM中，每一个状态代表一个可观察的事件，观察到的事件是状态的随机函数，因此该模型是一双重随机过程，其中状态转移过程是不可观测（隐蔽）的（马尔可夫链）。一个隐马尔可夫模型（HMM）是由五元组来描述的，即λ=（N,M,A,B,π），其中：

X={x1,…xN}：隐含状态，N为模型状态个数。

Y={y1,…yN}：观察符号集合，M为每个状态对应的可能观测符号数。

A={aij},aij=P(qt=Sj|qt-1=Si)：状态转移概率矩阵。

B={bj(k)},bj(k)=P(Ot=vk|qt=Sj),1≤j≤N,1≤k≤M：给定状态下，观察值概率分布矩阵。

π={πi},πi=P(q1=Si),πi≥0：初始状态概率分布。

在一个HMM模型里，可以描述一个未知的隐含状态在已知的观察状态下的状态转移过程。也就是在模型的各参数已知的情况下，给定观察序列O=o1,o2,…,ot，计算与序列O相对应的最佳状态序列Q=q1,q2,…qt，也就是HMM中的解码问题。所求的Q应当在某个准则下是“最优”的，因此也称Q为最优路径，解码问题即是确定最优路径的问题。

维特比算法（Viterbi algorithm）是一种动态规划算法，经常被应用于隐马尔科夫模型的解码问题中，它可以简单地描述为一种通过网格找到最可能路径的算法，在本文中指给定一个观察序列和HMM模型参数，有效选择“最优”状态序列，以“最好地解释”观察序列。

设状态空间为X，初始状态xi的概率为πi，状态转移概率矩阵为A，观察值概率分布矩阵为B，观察得到的输出为o1,o2,…,ot，则产生观察结果的最有可能的状态序列q1,q2,…,qt可由公式（3）和公式（4）递推得到：

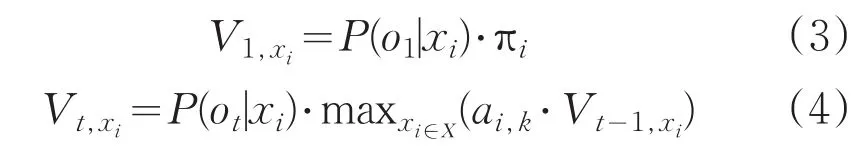
式中，前t个最终状态为xi的观测结果最有可能对应的状态序列的概率。通过保存向后指针记下在公式（4）中的状态可以获得维特比路径。另外设计一个函数Ptr(xi,t)，进行路径回溯。由此可得到式（5）：

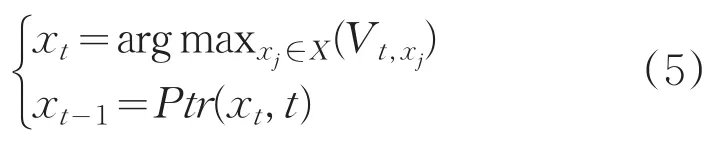
根据Viterbi算法，可以利用系统已知的观察状态，推断出最有可能的隐含状态，即下一个最可能的音符状态。

综上所述，已经可以确定HMM的隐含状态包含待学习音乐中的单个音符。根据本文定义，定义音符为隐含状态，音符发音时间的长短（时值）为观察状态。那么观察值概率分布矩阵就是统计一个音符在待学习音乐中所有可能的时值，以及它们出现的频率。

分别需要确定状态转移概率矩阵、观察值概率分布矩阵以及初始概率矩阵这3个参数。在确定了模型的隐含状态之后，可以统计出所有音符状态在待学习音乐片段中出现的次数。统计一个状态（音符）后所有的可能状态以及这些状态出现的频率作为状态之间的转移概率矩阵。如式（6）：

其中，1≤j≤n，n为当前状态Si所有可能的下一个状态的个数，N(Sk|Si)是当前状态Si的下一个状态Sk出现的次数，若某些状态后面没有出现过另一个状态则视作两者之间转移概率为零。例如图3，在“CDEDCDEFG”中，状态“C”并不会跳转到状态“E”。那么由状态“C”到状态“E”的转移概率记为零。

图3 CDEDCDEFG的音符转移概率。

观察值概率分布矩阵，是从某个隐含状态到某个观察状态的概率。定义音符为隐含状态，音符所对应的时值为观察状态。那么观察值概率分布矩阵就是统计一个音符在待学习的音乐片段中所有可能的时值，以及它们出现的频率。计算公式与状态转移概率矩阵相似，如式（7）：

其中，1≤k≤n，n为当前状态qi所有可能对应时值的个数，N(oi|qi）是当前状态qi对应时值为oi出现的次数。

初始状态矩阵分布决定模型的初始状态。本文分别统计每个待学习音乐片段中所有音符出现的次数。则某一音符的初始概率为式（8）：

其中，1≤i≤n，n为模型状态空间大小，N(qi)为状态qi在学习样本中出现的次数。某一状态的初始概率与其在样本集中出现的频率成正比，反映出这一状态在此样本集中的表现规律。

应用隐马尔科夫链学习每种音乐类别下的音乐片段，根据音乐片段中相邻音符的联系，确定初始概率矩阵、状态转移矩阵和观察值概率分布矩阵。

本文乐曲编码采用MIDI实数编码，编码范围为0-127，编码与音符一一对应，在程序中，采用midilinfo函数计算单个音符的开始时间和结束时间，并将两者之差记为该音符的时值，通过实验结果可知，古典音乐的音符编码范围在30到90之间，如图4谱例所示，谱例为一个音乐片段里的音符构成情况。一段音乐最终会被编码成一个矩阵。例如式（9）

其中，矩阵第一行为音高，第二行为时值。

图4 “Tear”片段的音符编码图4 音乐片段的音符编码

2.3 设计实验流程

实验选择30名面临毕业考试的大学生，其情绪因为考试压力而处于很焦虑的状态，因为不能确定哪种音乐对被试者影响比较大，所以选择了一些古典音乐、摇滚音乐、R&B音乐三种不同风格的纯音乐来影响受试者的情绪，分析脑电信号的变化。

首先让受试者聆听不同的音乐，同时记录受试者的EEG信号，利用Fast Ica和HHT算法开始去除眼电等伪迹的工作，并且进行特征提取，对情绪状态进行识别。如果某个时间段的情绪状态变好表明与此时对应的音乐片段起作用了，建立三个音乐子库，随之将此音乐片段截取下来进行分类，保存到各自对应的音乐子库。

2.4 结果分析

脑电处理结果示例：某位受试者聆听《D小调幻想曲》alpha与beta波单位时间功率比变化如图5所示。

图5 聆听《D小调幻想曲》的脑电变化

从上图可以看出，椭圆部分功率比变大，即alpha波功率增大，beta波功率减小，表示受试者情绪逐渐放松，则将与此时间段相对应的音乐片段截取并保存下来，N个由此而来的音乐片段组成了一个音乐库。

实验训练过程选择60首音乐进行训练，训练过程如图6所示。

图6 BP训练过程

然后每种风格各选200首音乐（共600首）进行测试。实验结果如表3所示。

表3 BP神经网络分类准确率

从表3可以看出，三种风格的正确率均在80%以上。

3 作曲实例

图7给出了基于HMM，将古典音乐库中的一些音乐片段连接起来的一个实例，共有439秒。由于音乐的五线谱占用篇幅较多，本文则用midi编码的方式呈现组合的音乐。

图7 音乐重组

4 结论

针对传统音乐治疗方法存在的问题，本文通过设计实验获得能够实时识别焦虑情绪的特征向量的阈值范围，实现对焦虑情绪的精准识别，精准把握每位人员的情绪变化，接着在对焦虑人员进行音乐治疗的过程中，基于脑电的实时反馈，获得对被试者有用的音乐片段，分析音乐特征，对所保存的音乐片段进行分类，在每个独立音乐类（古典音乐、摇滚、R&B）中，通过计算音乐片段里的各音符之间的转换概率，找到连接音乐片段的最佳顺序，组合成新的音乐。基于焦虑脑电反馈的音乐重组，不仅增加了音乐治疗的曲目，而且和原始音乐相比，重组的音乐对患者来说更有针对性，有利于对焦虑患者情绪的改善，可以达更好的效果，为音乐治疗领域的发展提供了新的途径。