半参数方法在缺失数据中的研究及应用

樊思敏，施三支，翟芳慧

（长春理工大学 理学院，长春 1300222）

在现实应用中，由于人为、机械等因素，数据缺失比较普遍。数据缺失造成的部分信息丢失，在不同程度上影响统计推断，导致得出结果存在一定的失真。数据缺失的处理研究引起了更多的关注。从缺失数据的缺失值排列方式来看，数据缺失可分为单调缺失和非单调缺失。从缺失数据的缺失影响因素来看，分为随机缺失（MAR）、非随机缺失（NMAR）和完全随机缺失（MCAR），缺失机制概念及三种缺失机制由 Rubin（1976）[1]提出。非随机依赖完全观测变量时，也可称为不可忽略机制（NI）。在不可忽视机制的基础上，由Samiran Sinha等（2014）[2]提出了NI-机制。本文主要讨论随机缺失下的非单调缺失情况。

缺失数据加大了数据分析和挖掘的困难程度，提高了分析结果的偏差。最简单的方式是删除带有缺失项的样本，即完全数据分析（CC）。样本量缺失项较少时，CC带来的偏差较少，当缺失项较多时，由于一部分的数据信息缺失，CC方法的偏差很大。为纠正由缺失数据导致的结论偏倚，缺失数据处理方法相继被提出。Horvitz和Thompson（1952）[3]最先提出了逆概率加权方法。Rubin和Laird（1977）[4]提出了用于处理缺失数据的EM算法。Zhao（1994）[5]提出了一类在MAR机制下的逆概率加权方法。Chen等（1999）[6]提出了一种用EM算法的全似然方法。Robins（2000）[7]提出了一种基于逆概率加权的改进方法，即逆概率删失加权法（IPCW）。Ibrahim，Chen（2004）[8]在不同缺失机制情况下，把半参数方法应用到多缺失协变量上。Samiran Sinha、Wang S.J和K.Saha（2014）[2]将半参数方法与NI-机制结合，应用到多变量缺失中。Jiwei Zhao和Jun Shao（2015）[9]基于不可忽视（NI）机制下提出了一种半参数似然方法。

本文对完全数据进行随机缺失，在随机缺失的背景下，使用了Samiran Sinha、Wang S.J和K.Saha（2014）[2]相似的半参数方法处理来达到估计Logistic模型中参数的目的，并与单一均值插补、多重插补和EM算法进行了比较分析。

1 半参数方法

记Y为因变量，X为带有缺失数据的自变量，Z为完全数据自变量，设定缺失自变量为2维的情况，样本量为h，数据类型为离散型。示性函数为I，当数据可观测时，示性函数为1，不可观测为0。

设Xij(i=1,2,…,h;j=1,2)表示为第i行第j列的观测值，Xi(-j)则表示为此观测值缺失。本文关注数据缺失的随机缺失，即缺失的数据与完全数据相关，假设缺失机制的选择概率为π，有：

设回归模型为g(Y|θ,Z,X)，θ为模型的参数。则似然函数为：

对上述似然函数取对数，对参数求导，得到得分函数如下：

其中，S=∂log(g(Y|θ,Z,X))/∂θ，ki,m(P)=g(Yi|θ,Zi,Xi)*P*f(Xir|Xi(-m),Zi)。

m的取值为1，2，12。P为相应的缺失选择概率，f(Xim|Xi(-m),Zi)为缺失项Xi(-m)的条件分布。由于缺失变量的条件分布未知，根据Chatterjee.N、Chen.Y.-H.和 Breslow.N.E（2003）[10]的理论可知：

当Ii1=Ii2=1，Ii=1。将得到的估计值代入得分函数，产生新的得分函数。对得分函数求导，得出目标参数θ。

与文献中不同的是，Samiran Sinha、Wang S.J和 K.Saha（2014）[2]在似然方程中与NI-机制结合，文中的应用数据模拟时进行随机缺失，故而在MAR的背景下，将似然函数方程（2）中缺失机制的选择概率设置为与MAR相对应的选择概率。

2 模拟与实证分析

文中采用的数据为太平洋车险数据[11]，数据量为50，数据量均为布尔型数值。因变量为车险理赔情况，自变量分别为调研者的性别、视力情况、抽烟史、是否有驾驶教育和相关年龄。由汪静波（2015）[11]变量与因变量的相关性可知，理赔与视力情况、抽烟史有关。设视力情况为X1，抽烟史为X2，由于半参数方法的需要，自变量的数量偏少，且MAR机制与完全数据相关，本文中再添加辅助变量Z=X1*X2作为完全观测数据。对两个自变量及辅助变量作共线性诊断，k的值为18.31，在100之内，可认为三者之间共线性小。

表1 自变量与因变量之间单因素logistic显著性

三个自变量与因变量的单因素Logistic分析结果如上，均呈现出显著性。

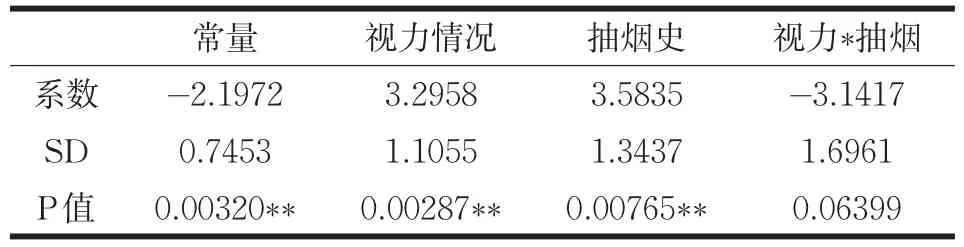
表2 Logistic回归分析

表2为因变量与自变量之间的回归分析结果，视力情况和抽烟史极为显著，视力*抽烟对方程的显著性不如视力情况和抽烟史。因此可得出实际应用数据的回归方程为：

设自变量X1、X2带有缺失项，Z为可完全观测数据，设置的缺失率分别为10%、20%、30%、40%，数据缺失模拟结果如表3所示。

表3为在不同缺失率的情况下不同缺失数据处理方法的结果。从表中可以看出，当缺失率为10%时，综合偏差和标准差来看，后三种方法相比均值方法效果稍微好些，当缺失率升至20%时，EM和半参数方法较均值插补和MI方法估计偏差更少。MI方法与均值插补相差不大。随着缺失率的进一步增大，这四种方法明显受到缺失率的影响，估计精度变差。而半参数方法较其他三种方法估计效果更好。

3 结论

在实际问题中，由于信息缺失，缺失的数据给研究者带来不少困扰。本文在离散变量背景下对完整的车险数据采用了Logistic回归，对自变量模拟了四种缺失率，在不同缺失率的情况下运用四种缺失数据处理方法来处理缺失数据以得到模型参数估计。从分析结果表中可知，缺失率越小，几种方法的估计精度越高。缺失率增加时，插补类方法明显差于模型法，而半参数方法受到的影响较其他几种方法小，有较好的鲁棒性。

插补类方法依赖数据之间的关系，对数据插补时有一定的偏倚，EM方法和半参数方法未直接对数据填补，利用似然函数处理缺失部分，对数据缺失处理有更大优势，而半参数方法自身结合参数和非参数优点，合理利用缺失部分信息，参数估计准确度和鲁棒性均高于EM算法，但半参数方法也受限于缺失机制，实现过程中受到初始参数的影响，这两者在将来都是值得探讨和改进的地方。

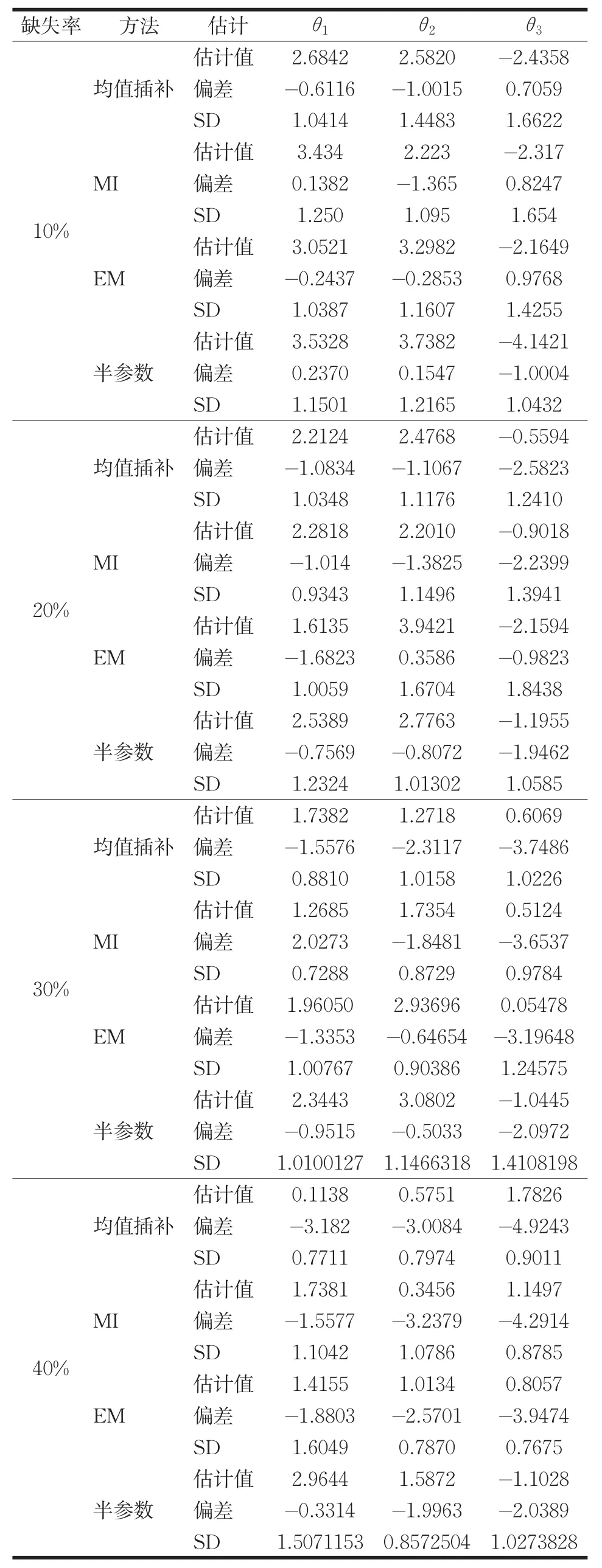
表3 不同缺失率模拟结果