六自由度机械臂运动学分析与轨迹优化

李珺茹，齐立群，韩文波

（长春理工大学 光电工程学院，长春 130022）

随着时代的进步，机器人技术的应用越来越普及，已逐渐渗透到军事、航天、医疗、日常生活等各个领域。机械臂作为机器人的重要执行机构，它的使用不但减少了劳动力降低了劳动成本，而且提高了产品的生产质量和效率，是未来发展的必然趋势。因此，对机械臂关键技术的研究具有重要的现实意义。运动学分析和轨迹规划是机械臂控制的两个重要因素。其中，机械臂的逆运动学问题是其轨迹规划与控制的基础，求解是否快速准确将直接影响到后续轨迹规划与控制的精度，而有效的轨迹规划能够确保运动轨迹在满足约束条件的前提下平滑准确[1]。基于上述内容，从实时性出发，采用PIEPER逆运动学解法，缩短了程序的运行时间。应用插补算法完成运动轨迹规划，并在笛卡尔空间中直观的得到末端执行器的路径曲线，通过优化算法减小轨迹偏移误差，结合MATLAB验证算法的合理性，为机械臂控制系统的实际应用提供了理论依据。

1 机械臂D-H模型建立

机械臂由一系列的关节和连杆按任意的顺序连接而成，这些关节可能是平移的或旋转的，连杆可能是任意长度的。所以，在对机械臂进行运动学分析时，必须先对机械臂进行建模。为了确定D-H参数模型，首先对机械臂的每个关节指定一个本地参考坐标系。

1.1 坐标系与参数的确立

如图1所示，zi轴与Ai+1关节轴重合，xi轴与公法线li重合，方向沿li由Ai+1轴线指向Ai+2轴线，yi轴按右手定则判定方向建立关节坐标系。

图1 连杆坐标系

定义连杆参数如下：θi为xi-1轴到xi绕轴zi旋转角度；di为xi-1轴到xi沿轴zi轴平移距离；li为zi-1到zi沿xi平移距离；αi为zi-1到zi绕xi旋转角度。相邻两坐标系之间的变化矩阵为

1.2 机械臂D-H参数模型

用D-H法来对机械臂建模分析，在每个关节建立坐标系，通过齐次变换描述坐标系之间的位姿变化[2]。本文采用的六自由度机械臂D-H参数如表1所示。

表1 六自由度机械臂D-H参数

1.3 六自由度机械臂正运动学分析

机械臂正运动学是指已知各关节的参数，求末端执行器相对于基坐标系的位姿[3]。由式（1）可得机械臂末端坐标系相对于基坐标系的变换矩阵。正运动学公式表示为：

式中，si代表 sinθi；ci代表 cosθi

变换矩阵T中，法线向量，指向向量，接近向量。如果直接给出有九个变量，比较麻烦，所以可通过RPY（滚动角、俯仰角和偏航角）给出。其中绕轴旋转φa为滚动角，绕轴旋转φo为俯仰角，绕轴旋转φn为偏航角。通过绕，，轴的三个旋转顺序即可把机械臂末端调整到相应的姿态。

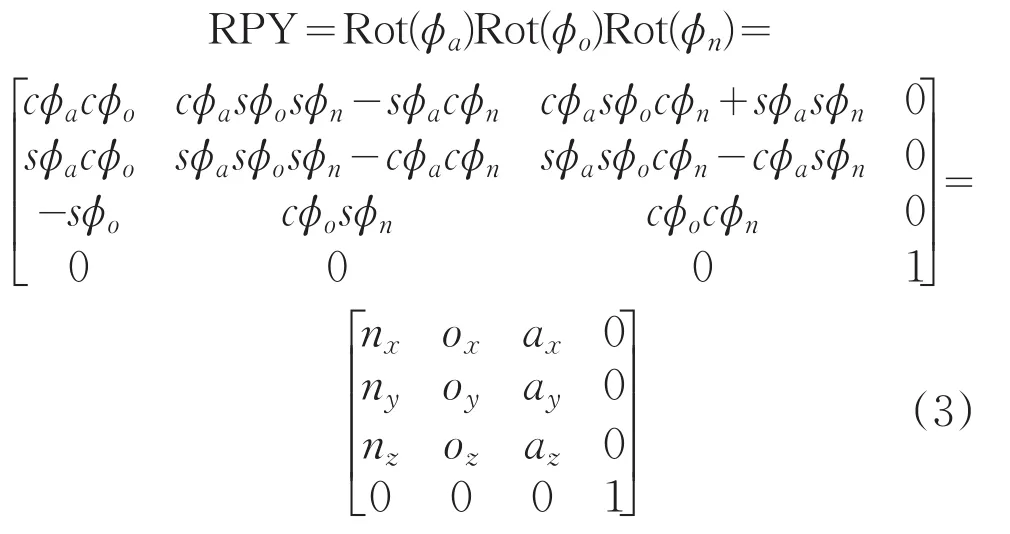
其中：

1.4 机械臂仿真模型搭建

对机械臂运动学的仿真研究，首先要建立机械臂的仿真模型。利用MATLAB Robotics Toolbox工具箱中的link（）函数和seriallink（）函数来搭建机械臂的仿真对象[4]。设定初始六个关节角分别为0，pi/2，-pi/2，-pi/2，0，pi/2；根据表1的D-H参数得如图2所示仿真模型。

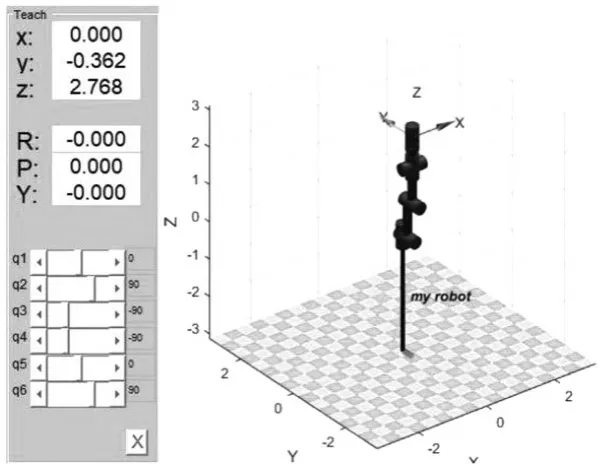
图2 机械臂仿真模型

2 逆运动学求解

逆运动学求解是根据给定的机械臂末端姿态和位置，求得六关节轴转动角度。根据模型图，可以将末端位置和姿态反解到后三个关节轴的交点，从而满足了Pieper准则[5]。将机械臂逆运动学的求解分为两部分，第一部分根据三轴相交点位置求解前三个关节角；第二部分通过已经求出的前三个关节角和给定的机械臂末端姿态求出后三个关节角。

2.1 前三个关节角的求解

根据已知末端执行器位姿反解出后三轴交点处的位置信息，表示为：

已知：

对于i=4，由式（1）的第四列有：

对于i=1,2,3由式（1）得：

将0A11A2带入（7）得：

式中，

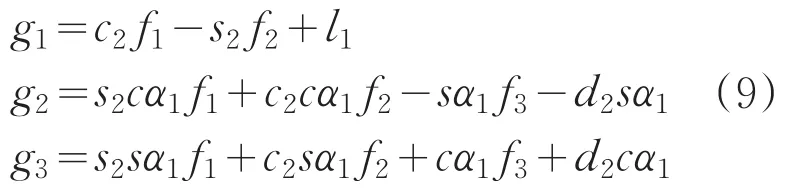
将（9）平方得：

令：

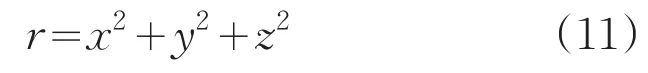
得：

将D-H参数带入（12）能够解出θ3：

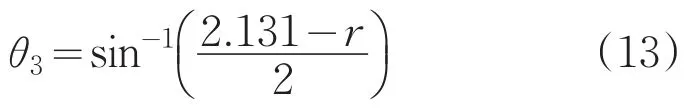
将θ3值带入（13），解出θ2：

将θ2,θ3带入（14），解出θ1：

2.2 后三个关节角的求解

后三个关节角的求解选择欧拉角变换的方法[6]。末端姿态矩阵与其他旋转矩阵有如下关系：

在求出θ1,θ2,θ3后，当θ4=θ5=θ6=0 时，可以由连杆坐标系6相对于基坐标系方位计算出0R6θ4=θ5=θ6=0 ，即

4R6ZYZ为Z-Y-Z欧拉角变换矩阵，其表达式为：

由这个矩阵可求得后三个关节角θ4=θ5=θ6。若可得到：

若θ5=0或θ5=180°，上式解将会退化，在这种情况下，仅能求出θ4,θ6的和或差。在这种情况下，一般取θ4=0，结果如下：

或

2.3 仿真验证

给定一个初始位姿(x,y,z,R,P,Y)，应用上一节的理论可以得到各个位姿所对应的六个关节角(θ1,θ2,θ3,θ4,θ5,θ6)；将这些关节角与输入到机械臂正运动学方程中与给定位姿比较，即可验证逆运动解的正确性。给定位姿（-1.165，-0.362，0.518，45，-60，0）。

表2 逆运动学验证

3 笛卡尔空间轨迹规划

机械臂末端执行器在直角坐标的位姿对时间函数进行的规划称作笛卡尔空间轨迹规划[7]。规划流程如图3所示，其中常用的插补算法有直线插补和圆弧插补。

图3 笛卡尔空间轨迹规划

3.1 空间直线插补轨迹规划

直线插补是机械臂的姿态变化按照给定的步长从初始姿态均匀向目标点姿态变化的过程。已知起点A(x0,y0,z0)，目标点B(x1,y1,z1)，插补次数N，则

对于该直线上的任意点有

已知空间中两点A(0,2,1)、B(3,12,9)，通过直线插补算法得到如图4所示轨迹曲线，证实了算法的可行性。

图4 直线插补

3.2 空间圆弧插补轨迹规划

已知不共线的三点A,B,C。它们确定了一个空间圆弧，用平面圆弧替换掉空间圆弧，从而将三维空间转化到二维平面空间，最后将规划好的坐标点转回到三维空间中去，即完成机械臂空间圆弧插补。

具体步骤如下：在基础坐标系中A=(x0,y0,z0)、B=(x1,y1,z1)、C=(x2,y2,z2)三点确定的空间圆弧，按右手定则建立局部坐标系O1X1Y1Z1。设圆心相对与基础坐标系的坐标为O=(a,b,c)，借助辅助点Q,P，如图5，可以得到

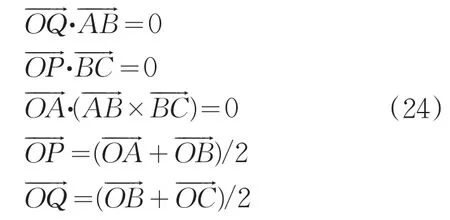
图5 二维平面坐标图

通过三元一次方程组，可得到圆心坐标O=(a,b,c)，圆弧半径，设点A到C对应的圆心角大小为φ，由图5得：

设插补次数为N，计算出每个插补点的坐标：

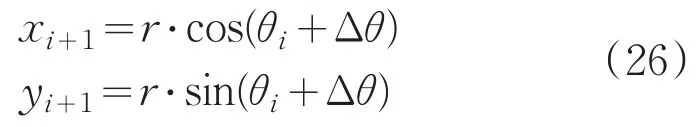
其中Δθ=φ/(N+1)。

在局部坐标系中求出了各个插值点坐标后，需要将这些点转换到全局坐标系中。令P表示由局部坐标系向全局坐标系的变换矩阵。P由O=(a,b,c)和X1，Y1，Z1矢量在全局坐标系中的方向余弦构成：

将X1，Y1，Z1化为单位向量，，即P可以表示为：

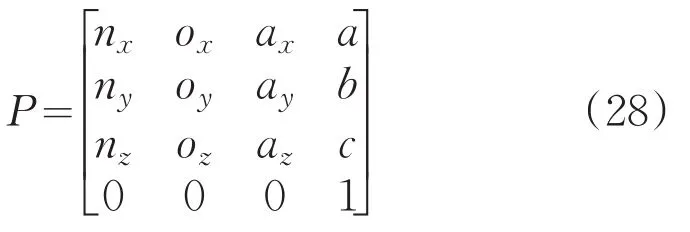
最后将局部坐标变换到全局坐标中：

已知不共线的三点A(3,12,9)、B(15,22,23)、C(25,26,25)分别为空间中不共线的三点，通过圆弧插补算法得到如图6所示轨迹，证明了机械臂圆弧插补算法是可行的。

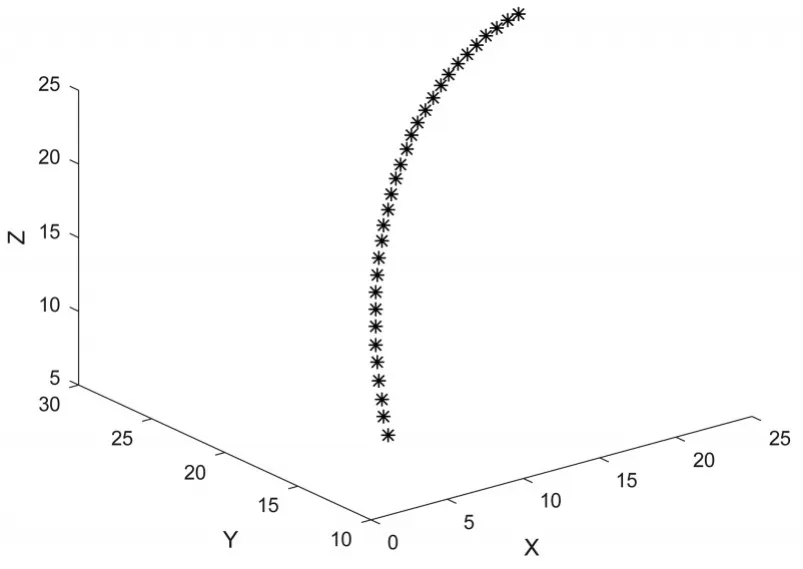
图6 空间圆弧插补

3.3 轨迹优化

如图7所示，在机械臂轨迹规划中，选用直线插补往往不能满足路径要求，通过对上一小节的分析，已知选取路径上任意不共线的三点即可完成空间圆弧轨迹拟合，选取的插值点不同，得到的轨迹拟合曲线也不同。插值点选取的优劣将直接影响到拟合轨迹的精度。为了得到误差值较小的拟合轨迹曲线，本文在位置控制方式中基于连续轨迹控制提出一种优化算法，通过选取不同插值点组合生成的轨迹曲线和预期轨迹曲线在空间中面积最小值的方法，得到最优插值点组合，完成机械臂轨迹曲线的优化。

图7 预期轨迹和算法拟合轨迹比较图

现给出如图7所示预期轨迹，应用优化算法按固定位置间隔分段选取插值点得到对应轨迹偏差。

如表3所示，通过比对各个插值点组的误差值，可以得到在插值中间点为（10.72，14.21，6.11）时误差最小，选择该点完成轨迹拟合，即可实现机械臂轨迹曲线的优化。

表3 插值点拟合轨迹误差

3.4 优化算法应用分析

六自由度机械臂轨迹优化算法为机械臂运动系统在空间的路径优化提供编程依据，在应用中，可根据本文提出的优化方案，将所有路径点按固定位置间隔分段，固定起点和终点，对选取的不同中间路径点分别进行曲线拟合，计算出轨迹偏差，通过比较各个拟合曲线误差值得到误差最小的插值点组合，完成该分段的轨迹优化。本文将该算法在机械臂运动控制软件编程环境LabVIEW下实现，实现流程图见图8.

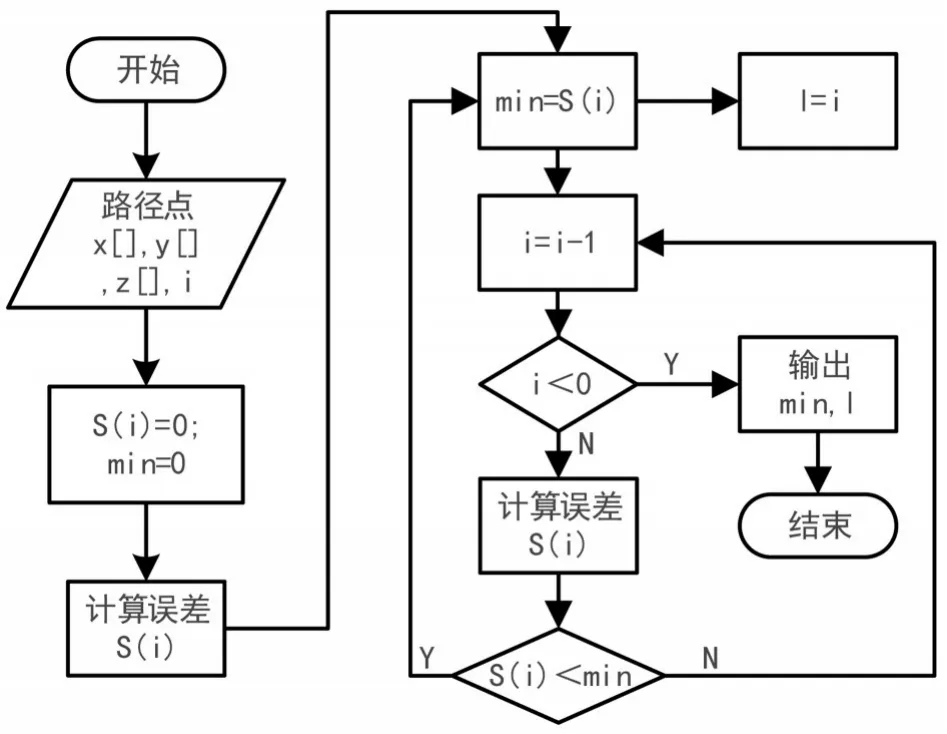
图8 轨迹优化算法流程图

如图9所示，在LabVIEW中输入预期路径点和分段插值点数后，可得最小误差值和对应的插值点组合，实现轨迹曲线的优化。

图9 笛卡尔空间轨迹优化

4 结论

针对一类具有典型结构的六自由度机械臂，在已知机械臂结构参数的基础上，选用D-H法建立机械臂的运动模型，采用PIEPER准则对逆运动学问题进行求解；通过对空间直线插补算法和空间圆弧插补算法的分析，使机械臂能够按照预先设定连续路径进行作业；针对空间曲线中轨迹偏移量较大的问题提出了一种优化方法，在LabVIEW中的Math-Script节点中导入该算法，直观的得到最优插值点组合，实现了轨迹优化，对机械臂在工业领域中的实际应用具有一定的指导意义。