机床工作台精度测试的球杆仪空间PPSPS机构方法

李晓鹏，王 智，王德伦

(大连理工大学 机械工程学院，辽宁 大连 116024)

0 引言

球杆仪是机床精度试验的推荐设备[1-2]。一个典型的应用是用球杆仪来评价两正交移动副的联动圆周运动，从中辨识出机床机械系统及其驱动系统的一些重要的精度指标[3-5]，如比例不匹配、不垂直度、反向越冲和反向间隙。由于球杆仪安装方便，可以进行高效的多轴同步圆周运动精度测试，球杆仪被广泛应用于机床和工业机器人的几何误差检测和辨识[6-8]。

球杆仪的测量数据中包含移动副的误差、驱动系统误差以及球杆仪的安装误差。现有的文献中通常假设球杆仪做平面运动，采用最小二乘圆拟合来消除安装误差，进而辨识出机床的几何误差[9-10]。本文提出一种基于PPSPS空间五杆机构的球杆仪测量机床两轴工作台的精度模型，不需要作平面假设，可以同时辨识出球杆仪安装位置误差、机床移动副的几何误差和运动误差，为机床移动副的精度检测提供了理论依据。

1 机床两轴工作台精度的球杆仪测量

1.1 球杆仪结构原理

球杆仪可看成一个SPS机构，由两个精密球(SA、SB)和一个高精度伸缩式线性传感器(PAB)组成。以机床移动副PX轴和PY轴工作台的圆测试为例，球杆仪上SB连接工作台，SA连接主轴，在测试过程中SA保持固定，使球杆仪SB绕SA做圆周运动，球杆仪记录下SA和SB之间的距离，如图1。在现有的方法中将球杆仪测量长度与标定长度的偏差表示为敏感方向上的运动副误差[6-7]。

图1 球杆仪安装示意图

1.2 球杆仪误差辨识

当存在安装误差时，球杆仪测量数据会出现正弦特性。Zargarbashi S H H等[9]建立了球杆仪平面测试的安装误差的数学模型，并提出了一种迭代最小二乘法来消除安装偏心。球杆仪的运动被假设为平面运动，球杆仪的安装误差被等价于圆心的偏差(u，v)，如图2所示。

图2 球杆仪的安装偏心

从消除安装偏心的测量数据中可以辨识出比例不匹配、垂直度、反向越冲和反向间隙等误差项。在现有的文献中，通常将球杆仪的测量值与球杆仪校准长度r之差Δr，向两个正交坐标轴方向投影，得到单个轴的误差分量：

Δr=(xΔX+yΔY)r

(1)

ΔX为PX的误差分量，ΔY为PY的误差分量。 建立几何误差模型(如多项式模型)，通过最小二乘法等方法进行数据拟合，解得误差函数的系数[4]。

(a)垂直度 (b)比例不匹配

(c)反向越冲 (d)反向间隙 图3 球杆仪检测的误差项

垂直度误差是指在机床测试部位PX轴和PY轴相互间不为90°，见图3a。设PX和PY不垂直度对PY轴误差分量系数δY，则PX和PY不垂直度α为:

(2)

比例不匹配误差是指在测试过程中被测量轴PX和PY间的行程差，见图3b。设PX轴的比例系数为a, PY轴的比例系数为b，则PX和PY的比例不匹配误差[11]E为：

E=2r(a-b)

(3)

反向越冲是机器轴在换向处非平稳反向运动而可能短时的粘性停顿产生的一个尖峰，见图3c；反向间隙主要由传动部件如丝杠、螺母等出现制造安装误差或磨损产生，见图3d。假定在某换向处，换向前圆图谱半径为rb，换向后圆图谱半径为rg，换向峰值处半径为rp，则反向间隙Δb和反向越冲Δp[12]为:

Δb=rg-rb
Δp=rp-rg

(4)

2 机床工作台精度测量的PPSPS机构

2.1 空间PPSPS机构

由图1，球杆仪的SPS运动链和两个待测移动副PX和PY可以组成空间五杆机构PPSPS，见图4a。PPSPS机构共有9个参数，其中有6个结构参数l0, l1, l2, α12, θ1, θ2，两个输入参数dY和dX和一个输出参数dAB。其中，dAB是球杆仪计算长度，对应球杆仪测量值；dY是移动副PY的位移，dX是移动副PX的位移；l0和θ1是定球心SA的位置和方向，l2和θ2是动球心SB的位置和方向，这4个参数由球杆仪安装后确定；l1是PY轴和PX轴的公垂线长度，α12是PY轴和PX轴之间的夹角，理想情况下α12=90°，这两个参数由机床本身的精度确定。

为了描述各参数之间的关系，过定球心SA建立固定坐标系{Of;i0,j0,k0}，移动副PX上建立运动坐标系{X;i2,j2,k2}。移动副PY运动轴线为k1，移动副PX运动轴线为k2，如图4a所示 。

(a)机构参数

(b)矢量图 图4 PPSPS机构参数与矢量图

矢量图见图4b，PPSPS的位移方程可由下式表示：

ROA+RAB=ROY+RYC+RCX+RXB

(5)

其中，RAB是定球心SA到动球心SB的矢量，其值为球杆仪的长度；ROY和RCX分别是PY和PX的位移矢量；ROA是过SA的矢量，且垂直于ROY，RXB是过SB的矢量，且垂直于RCX；RYC是PY和PX公垂线的矢量。将标量带入式(5)中，可得dAB的表达式：

(6)

其中，

V= -l0dXsθ1sα12+l2dYsθ2sα12+dXdYcα12

理想情况下，球杆仪的理论值dAB可由式(6)得到。然而由于两个移动副的误差运动，球杆仪的测量数据既包括式(6)中计算得到的理论值dAB，也包括移动副的运动误差。

2.2 PPSPS机构的运动学模型

(7)

其中，

(8)

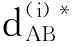
2.3 基于PPSPS机构的机床误差辨识

前文第1节中辨识出的机床误差也可以通过PPSPS机构拟合的方法得到。PPSPS机构的等效安装偏心δX和δY见图5，可以由PPSPS的结构参数得到δX=-l0sinθ1sinα12)，δY=l2sinθ2sinα12。

图5 球杆仪的等效安装偏心

两轴的垂直度误差也可以由结构参数得到：α12-π/2。

给定PX、PY轴的比例系数a、b，令输入参数dX=a×dX、dY=b×dY，带入式(8)中2次优化，优化变量为a、b，其他参数不变。两轴的比例不匹配为2r(a-b)，其中r为机床圆测试半径。比例不匹配的计算公式与1.2节中相同。

将PPSPS机构拟合得到的运动误差分别向PX、PY轴投影：

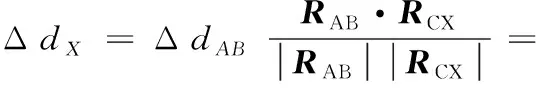
(9)

3 算例

3.1 球杆仪精确安装

如图6为球杆仪测量PX和PY联动的一组测量数据。

图6 球杆仪测量数据

用球杆仪测量移动副误差的球杆仪测量值，应用数学工具对模型(8)进行优化求解，解得最优解，见表1。

表1 机构拟合参数

用机构拟合得到的运动误差图与用最小二乘圆拟合得到的残余误差图一致，因此可以认为两种方法在球杆仪精确安装时是等效的。

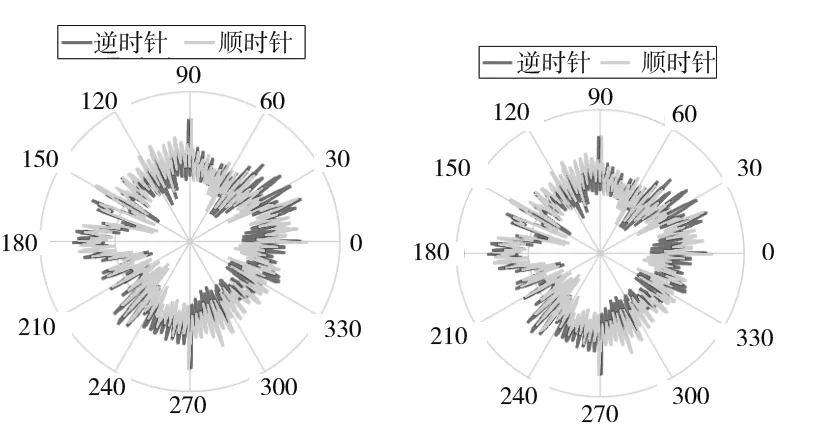
(a)PPSPS机构 (b)最小二乘法 图7 球杆仪测量数据拟合的残余误差

3.2 球杆仪任意位置安装

为了比较两种方法算得的圆测法的误差项，改变机床圆测试半径，分别用PPSPS机构法和最小二乘法对球杆仪测量数据分析，在不同安装模式下的测量结果如图8所示。

(a) 不垂直度 (b) 比例不匹配

(c) PX轴反向间隙 (d) PY轴反向间隙

(e) PX轴反向越冲 (f) PY轴反向越冲 图8 球杆仪测量数据的数据分析结果对比

由于采用机构学方法进行数据分析时，是将残余误差向两个空间矢量投影ROY和RCX投影(PY和PX的位移矢量)，而最小二乘法向平面两个坐标轴投影，因此误差项的计算结果略有不同。

从图8中可以看出，当改变机床圆测试半径时，由PPSPS机构法分析得到的误差项的值更稳定，而采用最小二乘法得到的结果波动较大。这说明PPSPS机构法的数据分析结果与球杆仪的安装位置无关，而采用最小二乘法的数据分析结果与安装位置有关。

4 结论

从球杆仪测试机床两轴工作台精度的实验结果可知，在球杆仪精确安装时，PPSPS机构法与最小二乘法是等效的；PPSPS机构法的数据分析结果与球杆仪的安装位置无关，而最小二乘法的数据分析结果受安装位置的影响较大。

PPSPS机构法不作平面假设，测试时不必将球杆仪平行于工作台平面安装，降低了球杆仪的使用条件；可以同时辨识出球杆仪的安装误差、两个机床移动副之间的方向偏差和运动误差，提高了球杆仪的精度测试的效率；基于PPSPS机构模型的数据分析方法，可以进一步辨识圆测试标准中规定的误差项，且误差项对应明确的几何意义。