范畴语法层级系统及其在自然语言计算中的优劣分析
姚从军,李奕丹
(湘潭大学 碧泉书院,湖南 湘潭 411105)
在范畴语法(简称CG)中,一个句法范畴的内部结构决定了在什么样的句法环境下,这个范畴的符号才能出现。在基本范畴语法(简称BCG)中,可以归结到如下结论:
如果范畴A/B可以从前件X推演出来,那么范畴A可以从前件X及在X右边与X毗连的范畴B推演出来;
如果范畴BA可以从前件X推演出来,那么范畴A可以从前件X及在X左边与X毗连的范畴B推演出来。
这两条是应用公理的冗长表述,对应于图1中的规则“/E”和“E”,它们给出了指派斜线范畴的必要条件。不过,条件不充分。如果把条件变成双向条件,得到了使用斜线范畴的充分必要条件,就产生了1958年版本的兰贝克演算(也叫原始兰贝克演算)[1]。在这个系统中,斜线范畴的行为受下面的规则支配:
如果范畴A/B可以从前件X推演出来,当且仅当范畴A可以从前件X及在X右边与X毗连的范畴B推演出来;
如果范畴BA可以从前件X推演出来,当且仅当范畴A可以从前件X及在X左边与X毗连的范畴B推演出来。
可使用后承规则图示精确地表达上述双向条件:
图1斜线算子的消去和引入规则
一个后承的前件不能为空,这是一个必需的附加条件。图1左栏的规则表述了上述双向条件的从左到右方向,它们等价于BCG的应用公理图示。如果把同一公理作为这里给出的规则的前提,就得到了公理表述。相反,也可以借助切割规则(即Cut)从应用公理推出图1的规则表述。这两个规则消除了斜线的一次出现,因此被称作斜线消除规则,分别简写为“/E”和“E”。
图1右栏的规则表述了上述双向条件的从右到左方向。它们是假设推理的实例:为了从某个前件X推出A/B,暂时在前件X的右外围增加一个范畴为B的假设,并设法推出后件A,然后解除假设,并得出A/B;为了从某个前件X推出AB,暂时在前件X的左外围增加一个范畴为B的假设,并设法推出后件A,然后解除假设,并得出AB。这些规则在推演中引入一个新斜线,因此,它们被称为斜线引入规则,分别简写为“/I”和“I”。
除了两个斜线之外,原始兰贝克演算还引入第三个范畴联结词“·”(称为积算子)。直观上说,一个表达式的范畴为A·B当且仅当它由一个范畴为A的成分和跟随其后的一个范畴为B的成分组成。因此,像“John introduced Bill to Sue and Harry to Sally”中的论元聚点“Bill to Sue”和“Harry to Sally”的范畴都为np·pp。换言之,积算子“·”可视为与后承前件中的逗号相对应的符号,该算子也由消去规则和引入规则来刻画。
图2积算子的消去和引入规则
消去和引入规则的使用及假设推理方法,使人联想到经典逻辑和直觉主义逻辑的自然演绎系统。范畴斜线类似于有方向的蕴涵,斜线算子消去规则(即应用规则)与蕴涵消去规则(即分离规则)相对应,而积算子与合取相关。这个相似性不是偶然的,兰贝克演算就是一个(非常简洁的)逻辑演算。接下来分析如何从经典命题逻辑一步步得到原始兰贝克演算,从而将此联系清晰地展示出来。
一、经典命题逻辑
(一)未进入层级的经典命题逻辑
考虑一个标准的经典命题演算的自然演绎系统,即图3所示的系统。把析取当作一个被定义的联结词,省略关于析取的规则。

图3后承格式的经典命题逻辑的自然演绎系统一
自然演绎系统(此后称为ND)一般由三部分组成。第一,像任意的演绎系统一样,它们包括同一公理和Cut规则。第二,可选择的结构规则,这些规则仅仅重新排列前件中的公式,不改变公式的内部结构。在上述系统中,只有一个这样的规则,即单调性规则(用M表示)。这个规则说,在一个有效的推演中,并非前件中的每个公式都会被使用,有的前件公式也许是多余的,必要时可以忽略。第三,逻辑规则,即针对每个逻辑联结词而言的引入规则和消去规则。在经典逻辑的ND系统中,前件被隐含地假定为公式集,集合中公式的顺序无关紧要,同一公式在前件中可以多次被使用。
(二)进入层级的经典命题逻辑
如果增加两个结构规则:交换规则(P)、缩并规则(C),就可以把经典逻辑置入结构层级之中。这两个规则表明:在这个演算中,可以交换公式的顺序,允许多次使用同一公式。

图4后承格式的经典命题逻辑的自然演绎系统二
有了这些结构规则的存在,我们可以为合取和蕴涵给出不同但是等价的结构规则(蕴涵的引入规则没变)。
图5 ∧和→的择换规则
可以证明,使用单调性规则和交换规则,可以从∧E′推出∧E(1)和∧E(2);使用缩并规则和切割规则,也可以从∧E(1)和∧E(2)推出∧E′。也可以证明,使用缩并规则和交换规则,可从∧I′可推出∧I;使用单调性规则和交换规则,可从∧I可推出∧I′。同样地,使用交换规则、缩并规则和单调性规则,蕴涵消去规则的两个版本也是可以相互推演的。
经典命题逻辑的特征公理是:((A→B)→A)→A。这一公理在接下来描述的所有逻辑中都不成立。
二、直觉主义逻辑及其子结构逻辑
(一)直觉主义逻辑
忽略进入层级的经典命题逻辑的关于否定的逻辑规则,我们就得到(正蕴涵的)直觉主义逻辑系统,这个逻辑比经典命题逻辑的肯定片段要弱。直觉主义逻辑仍然允许所有的结构规则,不过,作为这个演算基础的演绎概念不同于经典逻辑:经典逻辑关心柏拉图意义上的命题真值,演绎基本上是保持真值的;直觉主义逻辑关心证明,它是一个构造性逻辑,一个演绎是有效的当且仅当从前件的证明中能够构造后件的证明。因此,直觉主义的演绎概念类似于计算概念,并且可以把前件看作计算资源,它是资源自觉的(有资源意识的)逻辑。
图6后承格式的直觉主义逻辑的自然演绎系统
经典命题逻辑的特征公理在直觉主义逻辑中是不成立的,直觉主义逻辑的特征公理是:A →(B→A) 。然而,直觉主义逻辑的特征公理是经典命题逻辑的定理。
(二)相干逻辑
删掉单调性结构规则,就在面向自然语言计算处理的逻辑方向上又前进了一步。没有单调性规则,我们要求在一个计算中消耗掉所有的资源,即有效推演不允许前件含有多余的公式,这种方式得到的逻辑是一个相干逻辑版本。
在没有单调性规则的情况下,在经典逻辑和直觉主义逻辑中定义合取的两种方式不再等价。换句话说,直觉主义合取分裂成两个相干逻辑合取词。为避免混淆,我们使用不同的符号表示两个相干合取:∩、·。“∩”仍然读作合取,但是“·”读作积,图7给出相关的逻辑规则。

图7两类合取规则
图8后承格式的相干逻辑的自然演绎系统
在相干逻辑中,下面仍然成立:
A∩B⟹A·B
但是,
A·B⟹A∩B
是不可推演的。
经典命题逻辑的特征公理和直觉主义逻辑的特征公理在相干逻辑中是不成立的,相干逻辑的特征公理是:(A→A→B)→A→B。然而,相干逻辑的这一特征公理是经典命题逻辑和直觉主义逻辑的定理。
(三)线性逻辑
在相干逻辑中,一个推演必须消耗所有前件公式,但是可以任意多次地使用一个已知公式。一个更加资源自觉的推演假定,前件公式在推演过程中用一次即被耗费了,不可再用;因此,提供给推演的一个已知命题的实例的数量是至关重要的。这等于删掉了缩并结构规则,所得到的系统是线性逻辑(直觉主义逻辑的加法-乘法片段)。
图9后承格式的线性逻辑的自然演绎系统
在线性逻辑中,积和合取在逻辑上是彼此独立的,现在A∩B⟹A·B也不成立。
经典命题逻辑的特征公理、直觉主义逻辑的特征公理和相干逻辑的特征公理在线性逻辑中不成立,线性逻辑的特征公理是:(A→B→C)→B→A→C。然而,线性逻辑的这一特征公理是经典命题逻辑、直觉主义逻辑和相干逻辑的定理。
(四)兰贝克演算
在线性逻辑中,唯一被保留的结构规则是交换规则。如果我们删掉这个规则,蕴涵也分裂成两个变体(类似于上面结构层级中合取的进一步分裂)。
图10两类蕴涵规则
若有交换规则,则两个版本等价。如果不使用交换规则,就得到含两种蕴涵的逻辑。
图11后承格式的兰贝克演算的自然演绎系统一
如果略掉合取“∩”的规则,增加一个条件,即“后承的左边非空”,就得到原始的兰贝克演算。
图12后承格式的兰贝克演算的自然演绎系统二
值得注意的是,上面的说法不精确,延续兰贝克的记法,第一类蕴涵写作“/”,第二类蕴涵写作“”,所得到的逻辑才是兰贝克演算的版本。上述各特征公理在兰贝克演算中均不成立。
三、句法演算层级系统在自然语言计算处理中的优劣分析
到目前为止,我们这里所考虑的逻辑演算形成了一个强度递增的系统层级,兰贝克演算是这些系统中最弱的系统,经典逻辑是最强的系统。在直觉主义逻辑和兰贝克演算之间,各演算的区别由结构规则的去留决定,这就形成了针对结构规则模式而言的 “结构层级”,以及针对所有演算而言的“子结构逻辑”。这个层级概述见表1。
现在,我们拥有了可以使用的各种资源自觉的逻辑。接下来,我们也许想知道什么样的演绎概念与自然语言的句法组合相适应。单调性结构规则允许使用多余的前件公式,但是,自然语言不能容忍多余的语料,重复的语料也有一个清晰的句法功能,不是真正多余的。因此,一个合适的语法逻辑不会使用单调性结构规则。经典逻辑和直觉主义逻辑,因为包含单调性结构规则而与自然语言中的资源管理方式不太融洽。

表1 结构层级
带有缩并规则的逻辑允许资源的重复使用,不受限制的缩并规则对自然语言来说也太强,这等于随便删除相同成分(可能仅限于邻近的成分,取决于是否使用交换规则)。如果英语语法允许这样的运算,我们可能从(1)a的合语法性错误地得出(1)b也是合语法的。
(1)a.Anybody who laughed laughed about John.
b.Anybody who laughed about John.
由此看来,相干逻辑由于包含不受限制的缩并规则而与自然语言中的资源管理方式不太融洽。但是,照应现象表明,自然语言重复使用同一个资源是常有的事,如下所示:
(2)a.张三i喜欢自己i。
b.李四i知道张三j喜欢自己i /j。
在句法或语义计算中,(2)a中的“张三”要使用两次,因为“张三”是此句中“自己”的先行词;(2)b中的“李四”和“张三”之一要使用两次,根据此句中“自己”所选的先行词而定。自然语言中使用代词等索引词的表达式占全部表达式的70%以上,完全舍弃缩并规则显然不明智,引入一个受限制的缩并规则才是一个理智的选择。贾格尔引入受限的缩并规则,满海霞引入受限的强缩并规则,分别构造了含受限缩并规则的兰贝克演算LLC[2]和含受限强缩并规则的兰贝克演算LLCW′[3],允许后承前件中的资源重复使用,使用这样的系统可以方便地对自然语言中的照应结构进行计算。
带有交换规则的逻辑允许自由交换前件中的资源使用顺序,不受限制的交换规则对自然语言来说同样太强,因为这等于可以任意交换语料的使用顺序。虽然各种语言的词序自由度不同,但是没有任何语言在交换下封闭。如果汉语语法允许这样的运算,我们可能从(3)a的合语法性错误地得出(3)b也是合语法的。
(3)a.文强在夜晚离开程程。
b.文强离开在夜晚程程。
因此,不受限制的交换也不是语法资源系统的特征,线性逻辑由于包含不受限制的交换规则而与自然语言中的资源管理方式也不太融洽。但是各种自然语言的确具有不同程度的交换性,比如下面的两对语句都是合语法的汉语句,并且每对语句的一方均可视为根据交换规则从对方推演而产生的:
(4)a.张三吃了饭。
b.张三吃饭了。
(5)a.昨天小王回家了。
b.小王昨天回家了。
这样的现象在自然语言中大量存在,因此,完全舍弃交换规则也不可取,因为这样的系统无法计算自然语言中广泛存在的交换性。类似于缩并规则,使用受限的交换规则才是明智之举。比如,可以引入一个交换模态词△,设想用下面的规则替换交换规则:

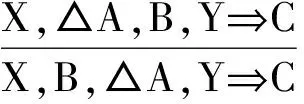
图13可选的交换规则替换版本
受限的交换规则∆P允许形如∆X的公式自由交换,左规则L允许在后承前件的公式前面自由增加一个∆-标记,右规则R允许在后承后件的公式前面自由增加一个∆-标记。
相对而言,原始的兰贝克演算是较符合语法一般目的的逻辑,因为它较好地体现了我们在自然语言中发现的一般的资源管理方式,故它是人们计算自然语言常用的系统。但是,对于自然语言来说,原始的兰贝克演算也有乏力之处,因为它完全舍弃了缩并规则和交换规则,无法处理自然语言中的确存在的语言资源重复使用现象和交换现象。另外,包括原始兰贝克演算在内的这些范畴语法层级系统都缺乏结合性的结构规则,如下所示:
图14结合规则
上述原始的兰贝克演算缺乏结合性结构规则,因此无法处理自然语言中存在的大量结合性结构,如例(6)所示。
(6)a.爸爸同意而妈妈反对我的建议。
b.张三喝啤酒很快而白酒很慢。
c.妈妈给了儿子一个苹果和女儿一根黄瓜。
上面都是合语法的语句。(6)a句需要运用结合规则,使主语“爸爸”和及物动词谓语“同意”进行组合运算,主语“妈妈”和及物动词谓语“反对”进行组合运算,得出的两个结果进行合并运算,所得结果与宾语“我的建议”进行运算,即可得到一个语句范畴s作为结论后承的后件;(6)b句需要运用结合规则,使宾语“啤酒”和状语“很快”进行组合运算,宾语“白酒”和状语“很慢”进行组合运算;(6)c句需要运用结合规则,使宾语“儿子”和 “一个苹果”进行组合运算,宾语“女儿”和 “一根黄瓜”进行组合运算。由于缺失结合规则、受限的交换规则和单调性规则,原始的兰贝克演算在自然语言的计算处理上也是不太令人满意。
原始的兰贝克演算是非结合和非交换的系统,常常简写为NL。在NL基础上加上规则A就形成了结合性的兰贝克演算L;在NL基础上加上规则P就形成了交换性的兰贝克演算NLP;在NL基础上加上规则A和P就形成了结合且交换的兰贝克演算LP。这就形成了兰贝克演算的子结构逻辑层级。就结合性的兰贝克演算而言,因其不受限制地使用结合规则,可以推出许多不合语法的英汉表达式,如下所示:
(7)a*[[The players]np[ [angrily] (s p)/(s p) [[ that came from Spain] np p [left] s p] s p] s p]s
b*[[[[爱程程]s p[[而他最终离开程程]ss]s p[的](np/np)s p] np/np[那个男人]np]np。
(7)a能够顺利推出的原因在于结合规则可使“that came from Spain”和“left”进行组合运算,(7)b能够顺利推出的原因在于结合规则可使“爱程程”和“而他最终离开程程”进行组合运算。因此,为了更好地对自然语言进行计算处理,必须对结合规则进行限制。
四、基于兰贝克演算对自然语言进行计算处理的困境与出路
如前所述,为刻画自然语言中语料资源重复使用的情况,贾格尔、满海霞分别在原始的兰贝克演算(即无交换规则和结合规则的兰贝克演算,简称NL)中增加了受限的缩并规则和强缩并规则,从而构造了含受限缩并规则的兰贝克演算系统LLC和含受限强缩并规则的兰贝克演算系统LLCW′。但是,这两个兰贝克演算系统都没有交换规则和结合规则,故无法描述自然语言具有的交换性和结合性。
如上所述,由对结合性和交换性结构规则的取舍不同产生了四个兰贝克演算系统,每个系统处于某一个子结构层面上,故每个系统只具有某个描述语料的模式,各有不同的计算分析特长,如NL系统长于对某些约束现象的计算分析,而L系统则适合处理非成分并列组合现象。然而,任何语言的结构都是丰富多彩的,任何一个系统都无法胜任对某一语言内的所有现象进行全面系统的计算分析,这就需要具有多个语言描述模式的复合系统。黑普(Hepple)[4]、姚从军等[5]合并任意多个子结构逻辑,限制结构规则,增加了包含规则,使各子结构层面相互连接,从而构造了各种混合范畴类型逻辑系统。为了保持对语料的敏感,混合范畴类型逻辑系统使用低层次子结构逻辑构造词库,而系统中的高层次子结构逻辑可以用来灵活地分析各种语言现象,这些良好的性质很适合用来对提取、话题句和非成分并列组合等现象进行计算处理。但是,这样的混合系统没有缩并规则,因而无法处理自然语言中大量存在的同一个语料在同一个句法生成树中多次使用的现象。
上面两种对自然语言进行计算处理的方式都是基于兰贝克演算的,各有一定的优势,但都有一定的不足之处。基于第一种处理方式的不足之处,可以设想在LLC和LLCW′中增加受限的交换规则和受限的结合规则。这种方式的难点在于如何给交换规则和结合规则施加限制,以及如何使用这些规则,一个想法是:给交换性或结合性的语料相对应的范畴加上模态词,在结构规则上显示只有具有某一模态词的范畴及其语料方可运用相应的结构规则,并且在词库中对相应的词条编码模态信息。基于第二种处理方式的不足之处,可以设想在各种混合范畴逻辑系统中,增加照应算子、照应范畴以及与照应相关的规则,特别是受限的缩并规则或者强缩并规则,为此,一种直接的想法是:把LLC或LLCW′与混合范畴逻辑系统嫁接在一起,或者融合在一起,构造“带受限缩并规则的混合范畴类型逻辑”或“带受限强缩并规则的混合范畴类型逻辑”。将这种直接的想法变成现实是笔者正在尝试做的工作。

