基于Canny算子加权引导滤波的Retinex医学图像增强算法∗

陈韵竹 郭剑辉

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

医学图像处理在计算机辅助诊断和治疗中起到越来越重要的作用。医学图像增强是检查图像以识别病灶并判断其意义的重要步骤。与磁共振MRI系统和CT扫描技术相比，X射线成像系统简单容易，耗时短、价格低廉。然而，其在成像过程中容易受到噪声等不良因素影响，导致医学图像普遍存在对比度、动态范围窄、强度分布不对称、边缘不清晰等问题。为解决以上问题，将图像增强技术并入医学图像处理可以提高图像的对比度，亮度和视觉质量。

目前，运用于医学图像的增强算法有很多种，如直方图均衡及其改进算法［1～3］、基于模糊集的图像增强技术［4］、Retinex及其改进算法［5～7］等。其中，Retinex算法应用最为广泛。Natarajan等［1］提出一种经自适应直方图均衡处理后的脑部图像再融合的增强算法。Sundaram等［3］提出了直方图修正乳腺X线照片图像的局部对比度增强。Sheeba Jenife等［4］提出了一种结合模糊逻辑和限制对比度直方图均衡的增强算法（FC-CLAHE）。Daniel J.Jobson等［5］首次提出多尺度Retinex增强算法，将可以提供动态范围压缩（使用较小尺度值）或色调补偿（使用较大尺度值）的单尺度Retinex进行加权结合，再通过色彩恢复算法，以实现图像的高动态范围压缩、色彩一致性、亮度保持等特性，但图像细节边缘处容易出现“光晕”。本文提出一种基于Canny算子加权引导滤波的Retinex算法，利用Canny边缘算子计算权重并用加权引导滤波代替高斯滤波估计光照分量，从而实现增强图像亮度、对比度的同时突出边缘细节，消除“光晕”伪影，提高图像清晰度和视觉质量，便于辅助医生诊断病理。

2 Retinex理论和引导滤波

2.1 Retinex理论

Land等［7］最早提出了Retinex模型，该模型的理论基础是依据人眼对色彩和光照的敏感程度。世界上所有物体展现的颜色都是以红绿蓝这三种颜色为基色，分配不同比例而来。而红绿蓝又取决于物体对不同波长的反射能力。如图1所示。Retinex理论［16～17］将摄像机中得到的像素值分为光照分量（亮度图像）和环境中物体的反射光分量（反射图像），其原理以表示为

其中，x、y为像素索引，I(x,y)为输入图像；S(x,y)表示环境亮度，即光照分量；R(x,y)为物体的反射分量。

图1 Retinex算法原理

Jobson等［8］在单尺度Retinex算法基础上提出多尺度Retienx算法，算法表达式为

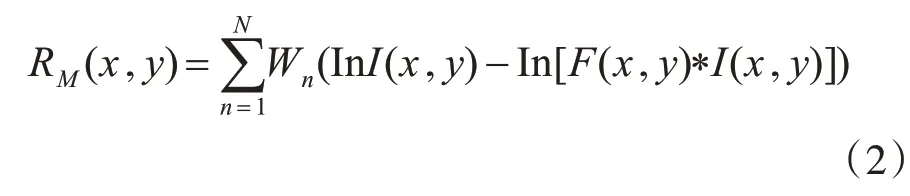
其中，I(x,y)为输出图像，即反射分量；F(x,y)为环境函数；*为卷积运算。Wn为加权系数（一般取1/3），n=(1,2,…,N)，N为尺度个数，ln为自然对数。环境函数可根据对光照估计的需求来进行选取，在使用高斯滤波之前主要是以下两种函数作为环境函数：Land［7］提出使用平方反比作为环境函数；Moore［9］等提出使用指数函数作为环境函数。在多尺度Retinex算法中使用高斯卷积函数作为环境函数对光照进行估计，其表达式为

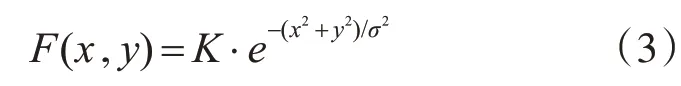
K为归一化因子，使得

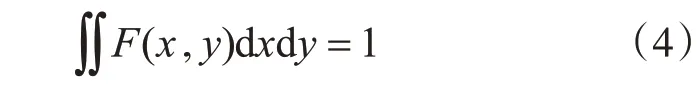
其中，σ为高斯函数的标准差，σ的大小决定了环境函数的滤波效果。σ取较大值，卷积后图像的平滑程度越高，但弱化了图像细节。σ越小，图像中细节越丰富，动态范围压缩能力较弱。所以，该算法选取三个尺度对图像进行滤波处理，一般为σ1＜50，50＜σ2＜100，σ3＞100［5］。

2.2 引导滤波

引导滤波器是于2009年提出的一种局部线性图像滤波器，对图像进行平滑滤波的同时还保持了边缘细节［10］。假设引导图像为Ii，输入图像为pi，输出图像为qi，其滤波线性转换模型为

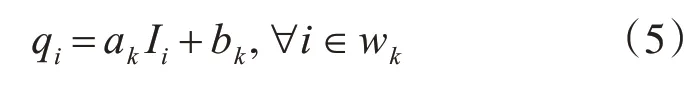
其中，i、k为像素索引，wk是以像素点k为中心、r为半径的方形邻域，（ak，bk）为窗口内的线性系数，定义为常量。

对式（5）两边求梯度，得

由式（6）可知，当引导图像Ii具有边缘信息时，输出图像qi也具有相似的边缘梯度。引导图像的平滑程度取决于ak的值。为了确定线性系数，要使输出图像qi和滤波器输入pi之间的差值最小［20］。求解滤波结果相当于最小化窗口wk内的代价函数。代价函数为

其中，pi为待滤波图像，ε为正则化因子，用来调节系数ak，ak防止过大。

3 基于Canny算子加权引导滤波的Retinex算法

传统Retinex算法中边缘容易出现“光晕”伪影现象，导致图像边缘模糊，不易确切诊断医学图像中的病灶区。所以，Retinex中的环境函数需要一种具有边缘感知的滤波器，而基于Canny算子加权引导滤波在平滑图像估计光照的同时保留了图像原有的边缘信息。本文提出了一种基于Canny算子加权引导滤波的Retienx算法。首先使用基于Canny算子的加权引导滤波代替传统多尺度Retinex算法中的高斯滤波进行光照估计，再转换到log域中计算出反射分量，最后经过量化处理得到输出图像。其算法表达式为

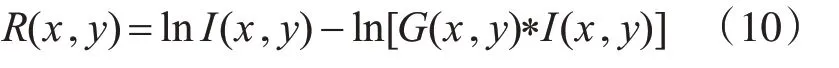
其中，R(x,y)为输出图像，即反射分量；I(x,y)为输入图像；G(x,y)为基于Canny算子的加权引导滤波，作为环境函数对光照进行估计；*为卷积运算。算法流程图如图2所示。

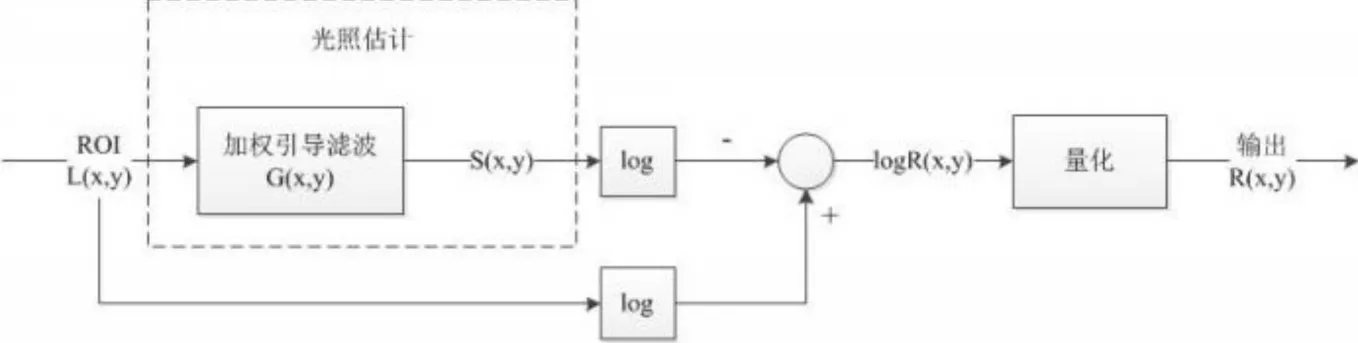
图2 基于Canny算子加权引导滤波的Retinex算法流程图

3.1 光照估计

Li等［11］首次提出加权引导滤波的概念，通过使用3×3窗口内的局部方差计算边缘权重，但并不是所有方差较大的区域都对应边缘区域，而且不能准确检测边缘处。本文选择使用基于Canny算子的边缘权重代替文献［11］中的局部方差。

Canny算子边缘权重定义为

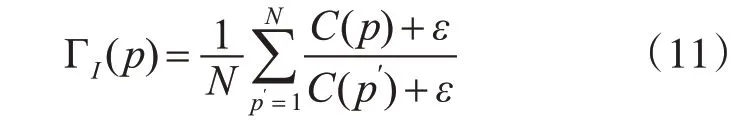
其中，ε为常量，一般定义为(0.001×L)2，L是输入图像的动态范围；I为引导图像；C(p)为p对应Canny算子的边缘值；N为像素总数。根据式（11）的边缘权重，其代价函数为

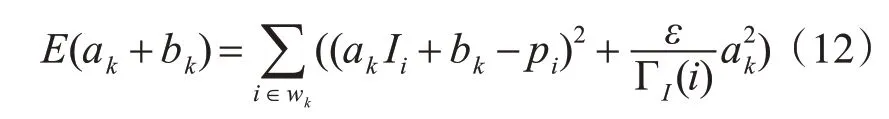
对式（12）进行最小二乘法，得

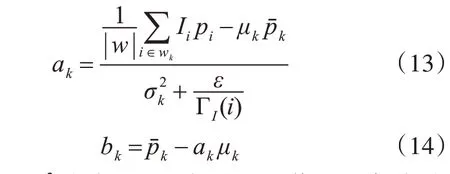
其中，μk和σ2k为窗口wk内引导图像I的灰度均值和方差， ||w为窗口内像素总数，pˉk为输入图像p在窗口wk内的灰度均值，ΓI(i)为图像边缘权重。

3.2 量化处理

由式（15）可知，R(x,y)是对数域上的输出，需量化到［0，255］的设备显示范围。对图像直接进行线性量化，公式如下其中，Rmax(x,y)和Rmin(x,y)分别为R(x,y)的最大值和最小值。上述方法简单易实现，但数据分布广且不均匀，难以满足医学图像的增强需求。本文使用GIMP处理程序中的量化方法［18～19］，具体如下：

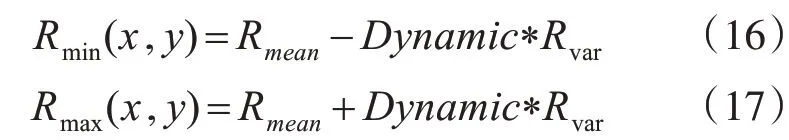
其中，Rmean和Rvar分别为R(x,y)中像素的均值和均方差；Dynamic为动态范围值；对每一像素进行线性量化

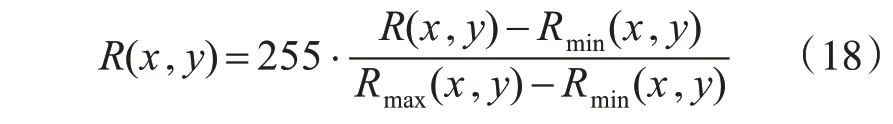
一般来说Dynamic取值在［2，3］。Retinex算法的关键在于对光照的估计方法，这一步骤直接影响到输出图像的清晰度、对比度以及增强效果［14］。

4 实验结果与分析

4.1 边缘权重对比

本文先后使用Canny算子、Sobel算子、Roberts算子对图像进行边缘权重的计算，结果如图3所示，Canny算子对原始图像边缘拟合效果最好。

图4（a）为胸部X射线图像，图4（b）和图4（c）是分别经过方差边缘检测［11］和Canny算子边缘检测后的边缘权重图。从图中明显可以看出，由Canny算子加权表示的图像边缘清晰、亮度均匀。因为Canny值在边缘细节处加权值比平滑区域处的大，所以图像边缘处权重ΓI(i)大于1，ak随之变大；平滑区域处权重小于1，从而ak变小。ε值和滤波窗口半径r的选取影响引导滤波的作用效果。

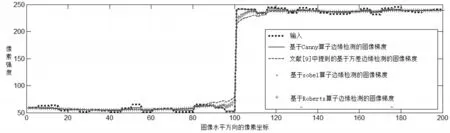
图3 不同边缘算子梯度图

图4 边缘权重

4.2 增强效果对比

图5、图6和图7将本文提出的算法与CLAHE方法、基于暗原色去雾算法［10］、多尺度Retinex算法［5］、基于引导滤波的Retinex算法［15］进行对比试验，结果表明本文提出的算法能够简单有效地提高图像对比度。

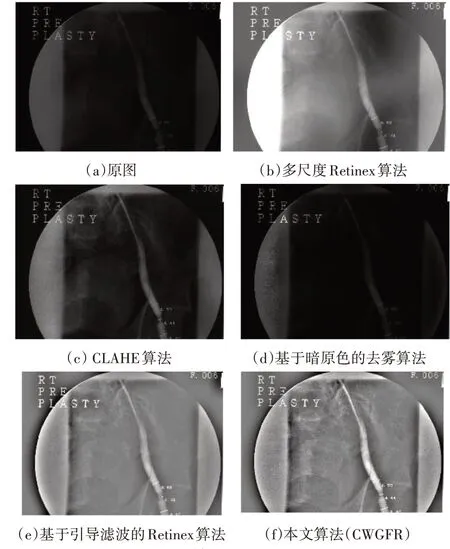
图5 血管增强效果对比图

多尺度Retinex算法在计算光照时［5］以一个单一像素为中心，只是根据邻域像素离中心像素的距离计算权重来估算当前像素的照度，而没有考虑像素亮度本身，计算结果将不准确。另外，本算法是在基于引导滤波的Retinex算法［15］的方法的基础上引入了Canny算子，实现具有边缘感知特性的引导滤波，解决由于方差边缘权重导致的边缘亮度不均匀，边界过度不自然等问题。从图5可以明显看出，利用本文算法增强后的血管图像边缘清晰，亮度均匀，增强效果明显。基于暗原色的去雾算法针对低对比度的医学图像，增强效果不佳。图6经过本文算法增强后，肺部若出现结节、钙化点等异常情况更加易于诊断和治疗。CLAHE算法处理医学图像存在亮度过饱和现象，可能会引入噪声。

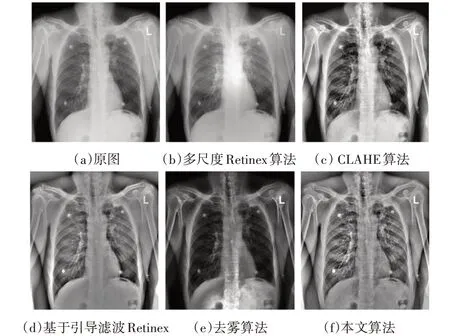
图6 胸部增强效果对比图

4.3 算法效率分析

针对算法运行效率，本文分别与上述四种算法进行比较。引导滤波中使用了盒式滤波，其时间复杂度与窗口大小无关的，即使采用大窗口处理图像，时间复杂度也保持不变，效率更高。

实验采用NASA数据库图像，Matlab 8.3.0（R2014a）实现，计算机处理器为双核2.30 GHz、内存为4GB。表1为各个算法处理图像所用时间的对比结果。

表1 运行时间对比结果（单位：s）

4.4 图像质量评价

对增强后图像的质量可以通过主观和客观评价方法同时进行评估。针对医学图像，增强的效果和部位根据不同检测区域的需要具有不同的侧重点。对于胸片和乳腺图片等，可能需要突出钙化点、肿瘤、炎症等特征；对于骨骼X射线图像，需要的清晰的骨骼边缘以检测骨骼异常、骨刺、骨质增生等问题。

表2 PSNR对比结果

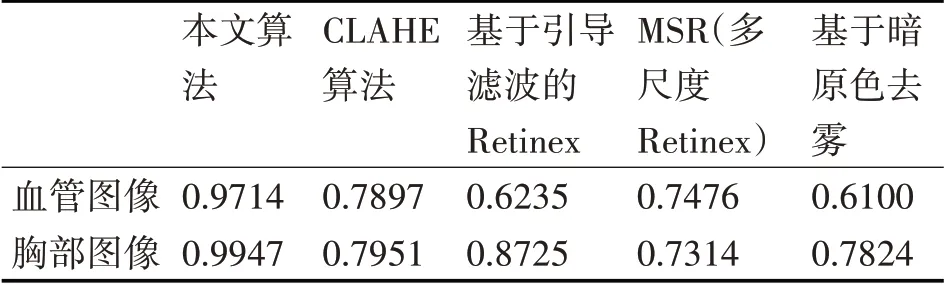
表3 SSIM对比结果

本文选用两种客观质量评估方法，分别为峰值信噪比（PSNR）和结构相似度（SSIM）［16］，对五种算法增强后的图像进行对比。结合表1、表2和图10的对比结果，本文提出算法时间复杂度为O（n），经过图像质量评估指标对比，性能较好，适用性更强。

5 结语

本文提出一种新的基于Canny算子加权引导滤波的Retinex图像增强算法，首先利用引导滤波代替多尺度Retinex算法中常用的高斯滤波对照度进行估计，然后再传统引导滤波的基础上引入Canny算子进行边缘权重的计算。

实验结果表明，本文提出的方法不仅能快捷有效地增强医学图像对比度，还能保持原图像所具备的边缘特性，有效消除“光晕”现象，对辅助医生诊断病理有很大帮助，在计算效率、增强质量方面有明显优势。