考虑时滞影响的绞吸挖泥船产量预测∗

陈秀静 倪福生 魏长赟 杨金宝

（1.疏浚技术教育部工程研究中心 常州 213022）（2.河海大学机电工程学院 常州 213022）

1 引言

疏浚是水利水运工程的重要项目之一。现代疏浚作业主要依靠挖泥船进行，其中绞吸挖泥船具有生产效率高、适用范围广等优点，所以被广泛运用在疏浚作业中［1］。疏浚施工过程中，绞吸挖泥船的产量直接决定了工程效益，因此，预测绞吸挖泥船产量具有重要的意义。预测绞吸挖泥船产量有助于提高施工效率，可以有效地仿真疏浚过程，同时有利于最优选择疏浚作业参数，实现挖泥船的优化控制。然而，影响挖泥船产量的因素较多且相互关联。这不仅涉及到施工现场的土质、风向、潮位以及船体硬件等客观因素，还包括施工工艺、船员心情等一些主观的因素。因此，绞吸挖泥船产量的预测问题非常复杂。而神经网络具有较强的非线性和良好的泛化能力，可以很好地处理复杂的非线性问题，将神经网络的方法运用到研究挖泥船疏浚作业过程，具有较强的优势。张硕［2］等运用数据驱动建模技术建立耙吸挖泥船疏浚作业产量模型，将神经网络算法与遗传算法结合，应用于产量优化问题；闭治跃［3］等建立基于RBF神经网络的泥浆浓度软测量模型，为疏浚工程提供一种简单可靠、成本低廉的泥浆浓度在线连续测量的新方法。本文选取了影响绞吸挖泥船产量的四个主要因素（绞刀电机电流、流速、吸入真空、横移速度），以泥浆浓度作为输出因素，重点考虑了泥浆浓度与所要研究的因素之间的时间滞后问题，建立了带有时滞的BP神经网络模型，对绞吸挖泥船产量进行预测。

2 BP神经网络模型

BP（Back-Propagation）神经网络是一种多层前馈神经网络，3层BP网络的拓扑关系如图1所示，此网络包含输入层节点，输出层节点和一层隐含层节点。上下层之间实现全连接，而同层神经元之间无连接［4］。

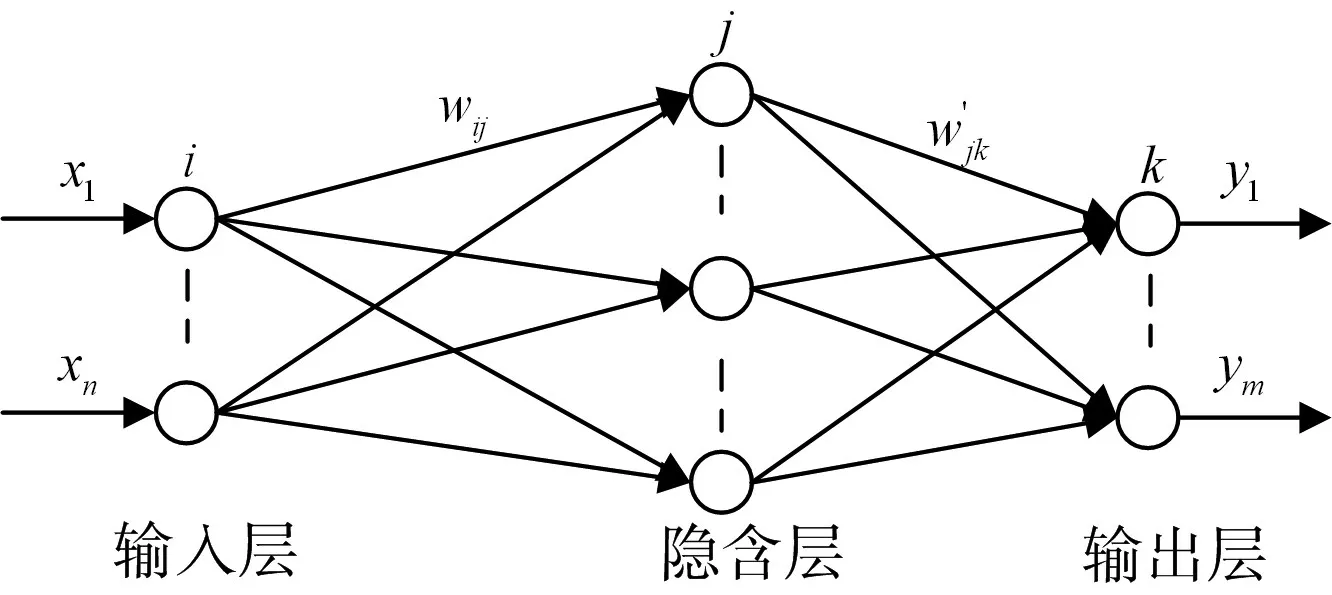
图1 3层BP神经网络结构

BP神经网络的基本原理是采用梯度下降法不断调整权值和阈值，使得网络的实际输出值和期望输出值的均方误差最小［5］。BP算法是输入学习样本后，神经元的激活值从输入层经隐含层向输出层传播，计算实际输出，而网络训练误差从输出到输入，并进行隐含层和输出层权值、阈值的修正［6］。标准的BP算法存在收敛速度慢、易陷入“局部极小值”等缺点［7～8］。因此，这里采用改进的LM学习算法改善网络的性能。

3 产量模型的建立

3.1 产量模型变量的选择

绞吸挖泥船的产量公式为

产量=流量Q*泥浆浓度Cw*工作时间t。其中，流量Q=管道流速v*管道横截面积A，在挖泥船正常施工过程中，管道横截面积和挖泥时间是固定的，管道中的流速变化比较小，可以说基本保持在一定的数量级不变，所以可以用泥浆浓度曲线近似替代产量曲线来研究绞吸挖泥船产量［9］。

图2 绞吸挖泥船结构

绞吸挖泥船的结构如图2所示，其疏浚过程由土壤切削、泥浆输送、船体横移、台车步进四个子过程协调作业完成。

绞吸挖泥船的挖掘作业是通过绞刀的连续旋转运动完成的。绞刀安装在桥架末端，由一台水下电机驱动。这一过程中，绞刀的性能直接反映了绞吸挖泥船的切削能力，从而影响绞吸挖泥船产量，而绞刀是由电机驱动的。因此，本文通过分析施工现场采集的数据，选取绞刀电机电流这一参数反映土壤切削过程对挖泥船产量的影响。

挖泥船完成一点的切削后，通过横移系统的作用，使船体以定位桩为中心呈扇形移动。由于挖泥船的产量是由绞刀切削的泥砂质量决定的，即泥浆的浓度主要对象是泥砂质量。而绞刀切下的泥砂体积量的公式为

式中，V为泥砂体积量；b为切削宽度；d为切削深度；Vc为横移速度。

则单位时间内绞刀切削泥沙质量就为

但是在实际施工过程中，被绞刀切削下来的泥土并没有全部被绞刀头后部的吸入口吸入输泥管，被漏掉的那些泥土会慢慢沉淀回河底，可以用漏泥率k（0≤k≤1）表征，能顺利由吸泥口进入输泥管的泥土质量Mc：

式中

被成功吸入的泥水混合物，经吸泥管进入泥泵；在泥泵内充分混合形成泥浆；泥浆排出泥泵后具有一定的压力和流速，经排泥管线输送到排泥场。泥浆在输送过程中，还存在一定的沿程损失。沿程损失计算公式为

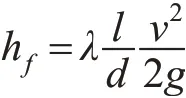
式中，l为输送管道的长度；d为输送管道的管径；v为管道截面的平均流速；g为重力加速度；λ为沿程阻力系数，也称达西系数。一般由实验确定。

完成此处定位桩控制范围内的挖泥后，通过换桩系统使挖泥船整体前移，进入下一个挖泥作业，即为台车步进过程。

在疏浚作业中，水下真空表安装在绞刀上部，对管路中泥浆浓度的变化非常敏感，一旦绞刀切削到土壤，吸泥口吸泥之后，泥浆开始在管路中输送，真空表示数将发生突变。因此，真空度数实时反映挖泥船的产量率。

综合上述分析，本文选取绞刀电机电流、横移速度、真空度和管路流速这四个参数作为神经网络模型的输入因素，选取泥浆浓度作为输出因素。

该神经网络模型的输入因素与输出因素之间并不是实时一一对应的，它们之间的对应关系较为复杂。实际疏浚过程中，系统采集疏浚参数时基本都靠仪器仪表来进行的，测量流速的流量计、测量真空度的真空度表等仪器并不是和测量泥浆浓度的浓度计安装在相同位置，也就是说这些仪器之间存在位置差，这就会出现时滞问题。可能会出现绞刀开始切削土壤，绞刀电机已经开始工作，而此时泥浆输送系统还没有将泥浆输送到浓度计安装位置的情况。故应当考虑去除时间滞后，才能更好地进行建模。由于影响滞后问题的因素有很多，通过认真分析挖泥船施工参数，本文选取真空度作为主要因素，重点考虑真空度与泥浆浓度的滞后问题，选取合适的解决时滞的方法，建立绞吸挖泥船预测模型。

3.2 产量模型的建立

通过上述分析，可以得出真空度与泥浆浓度有很大的关系，直接反映了绞吸挖泥船产量的大小，故本文首先建立真空度与泥浆浓度的预测模型。选取某绞吸挖泥船现场采集的实测数据，通过编写的数据筛选程序，筛选出有用数据，用BP神经网络建模。由于选取的各输入数据具有不同的物理意义和不同的量纲，数据间差异较大，为了使网络具有良好的泛化能力，应用Matlab自带的归一化函数premnmx进行数据归一化，使所用数据在-1～1之间。神经网络结构为1-5-1，即输入层有一个神经元，隐含层有5个神经元，输出层有1个神经元。隐含层神经元的传递函数为tansig函数，输出层神经元的传递函数采用purelin函数，期望误差设定为0.01，学习率设为0.1，训练次数为5000，采用LM-BP算法，训练函数为trainlm，通过Matlab调用神经网络工具箱进行建模，以真空度作为输入，泥浆浓度作为输出，建立预测模型。预测曲线如图3所示。

与泥浆浓度这一参数相关的绞刀电机电流、流速、吸入真空、横移速度这些参数就并不是一一对应的了，可能这一时刻采集的输入参数对应的是后面某一时刻的泥浆浓度参数。这种现象反映在预测曲线上就是：单一输入因素（绞刀电机电流、流速、吸入真空、横移速度）预测泥浆浓度时，预测曲线与实际曲线就会存在时滞问题，因而预测曲线与实际曲线只是走向大致相同，两曲线的拟合度存在较大差异，如图3所示。从图3可以看出，以真空度作为输入因素预测出来的泥浆浓度值与实际泥浆浓度值的曲线走向大致相似，这说明真空度可以很好地反映泥浆浓度的变化趋势。同时，从图中也可以看出，预测值与实际值之间存在明显的时间延迟和滞后问题。原因有：从绞刀头到浓度计安装位置有一定的管线长度，如图2所示为L1+L2+L3+L4的长度，所以当绞刀开始切削土层时，管道中的泥浆还未到达产量计安装位置处，这需要一个时间的过程，引起了延迟上升现象；同样的，当绞刀停止切削时，管道内还存在残留泥浆要经过产量计安装位置处，产量计还在计算产量，引起了滞后下降现象；同时，产量的计算不是线性的，产量和时间呈指数关系，这也会引起延迟和滞后现象。由于存在这种时滞问题，导致这些输入因素并不是对应此时的泥浆浓度，而是对应后面某一时刻的泥浆浓度值，所以在预测绞吸挖泥船产量时，可能会得到错误的预测曲线。正因如此，在预测绞吸挖泥船产量时，这种时滞问题必须得到解决，才能更加准确地得出预测结果。

图3 真空度预测图

以真空度与泥浆浓度预测模型为例，考虑时滞问题，加入时间延迟和滞后模型，其他参数不变，得到的预测曲线如图4所示。

图4 去除时滞后的预测曲线

由图4可知，加入时滞模型以后，预测曲线与实际曲线之间基本不存在时间的延迟和滞后问题，这说明本文所用的去除滞后的方法是可行的，可以用于解决实际挖泥船产量计算过程中的时滞问题。由于去除了时滞，该BP神经网络模型较好地实现了对绞吸挖泥船产量的预测，预测值与实际值的吻合度较高，相关性较大。但是，由图4可以看出，预测曲线与实际曲线还存在一定程度的差异，这是因为影响绞吸挖泥船产量的因素有很多，而只以真空度这一主要因素对其进行预测，所以存在一定的差别。故本文运用绞刀电机电流、横移速度、真空度、管路流速这四种对绞吸挖泥船产量有较大影响的参数作为输入因素，通过滞后模型去除时间滞后问题，建立预测模型，对绞吸挖泥船产量进行预测。该模型隐含层神经元数目为10个，其他参数不变，预测曲线如图5所示。

图5 多因素的预测曲线

由图5可以看出，以绞刀电机电流、横移速度、真空度、管路流速四因素作为输入变量的绞吸挖泥船泥浆浓度预测曲线与实际曲线吻合度更高，基本可以实现对泥浆浓度的预测。由于泥浆浓度变化可以在一定程度上反映挖泥船产量的变化，故也可以间接实现对绞吸挖泥船产量较为准确的预测。

4 结语

本文提出了带有时滞的BP神经网络预测模型，重点考虑了真空度与泥浆浓度的时间延迟和滞后问题，以绞刀电机电流、流速、真空度和横移速度作为神经网络模型的输入因素，以泥浆浓度作为输出因素，对挖泥船产量进行预测。预测结果表明，该模型可以有效地预测绞吸挖泥船产量，具有一定的预测精度，可以用于绞吸挖泥船的仿真模拟，也可用于实际绞吸挖泥船产量的预测评估。