基于Gray-Markov的贵州省物流量预测

纪兆南 （贵州大学 管理学院，贵州 贵阳 550025）

0 引言

物流量是指某地区在一定时期内发生的货物流通量的总称，它是反映一个地区经济发展水平和增长速度的重要参考指标，对于地区的物流规划与决策起着非常重要的作用。通过文献研究发现，在研究物流量问题时，大多以货物运输量代替[1]。目前国内有很多对地区货运量或者物流需求量进行预测的文章，基本的预测方法有回归分析法、时间序列法、指数平滑法等[1]，这些方法模型都是通过对原始数据进行拟合分析后进行数据预测，它们共同的特点是对拟合精度的错误认识以及并没有考虑事物本身复杂的多样性。而灰色预测方法具有所需信息量少、能将无序序列转换成有序序列的特点，能够大大提高预测的精度；马尔科夫链模型适用于随机波动较大的问题的预测[2]。将两种预测模型结合起来，先用GM 1,（）1模型进行预测，再利用马尔科夫链对预测结果进行修正，大大提高预测的精准度，以达到科学预测分析的目的。

1 灰色—马尔科夫模型构建

1.1 灰色GM 1,（）1模型构建

灰色GM 1,（）1模型是灰色系统理论中最为常用的一种预测方法，其原理是通过对原始数据进行累加后生成一个更具有明显规律的新序列[3]，再对生成序列进行重新建模。用生成模型得到的数据进行逆处理得到还原模型，再用还原模型进行预测。灰色预测GM 1,（）1建模的具体步骤如下：

设原始数据序列X（0 ）有n个观测值对原始数据进行一次累加生成序列对其进行一阶微分可得到其中为待识别的灰色参数，按照最小二乘法可求得

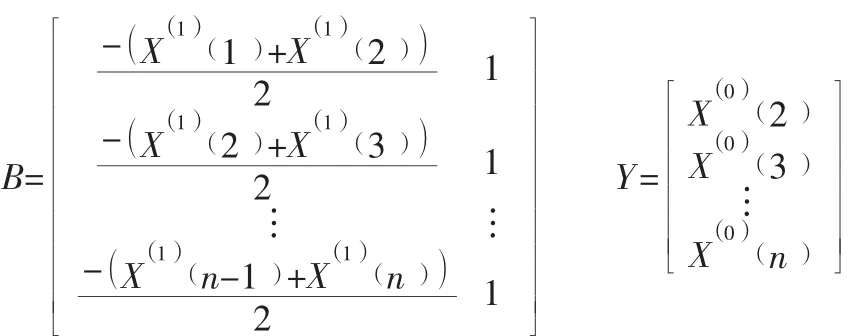
将得到的a,u值代入式子得到最后对其进行累减得到X（）0的预测模型为

1.2 马尔科夫链模型

灰色GM（ 1,1）模型由于原始数据的不稳定性，很难将预测区间限制在很小的范围内，精度要求远远达不到要求[7]。而马尔科夫链模型就很好地解决了这个问题，将灰色GM（ 1,1）预测的值用马尔科夫链进行改进，可以大大提高精度。

马尔科夫是根据现有的状态及状态转移的规律，预测未来可能出现的状态，可通过式子x（k+1）=x（k）*p得到。其中x（k）为t=k时间的状态向量，p为一步转移矩阵，x（k+1）为t=k+1时间的状态向量。

1.3 灰色马尔科夫模型构建

1.4 灰色预测值的修正

通过马尔科夫状态转移概率矩阵，预测灰色预测值的相对误差状态区间为取得相对误差状态区间的中值作为灰色预测值的修正值y[9]，计算公式为当灰色预测值比实际高估时，上面公式中分母加减号取正值；当低估时，应取符号；当较为准确时，不用修正。

2 贵州物流量预测实证分析

物流量是指一个地区通过不同的运输方式（包括公路、水路、铁路等方式）所产生的运输量。物流量作为物流需求的重要指标之一，在物流规划、物流资源分配以及物流产业布局等方面起着重要的作用。贵州省由于地形、资源的条件限制，省内92%货运都是通过公路货运完成的，物流量的不断上涨，表明了贵州省的经济发展对物流需求量日益增加。通过对贵州省物流量的统计发现，近10年来省内货物运输量一直呈现持续上涨的趋势。因此，探索未来贵州省的物流量规模，可以为运输市场的良性健康发展提供方向，为贵州省进行大物流格局的规划和决策提供依据。

2.1 GM（ 1,1）模型构建与预测

以贵州省2006～2015年的货运量数据作为原始数据，如表1所示：

表1 2006～2015年贵州省货运量数据 单位：万吨

贵州省货运量原始数列为：

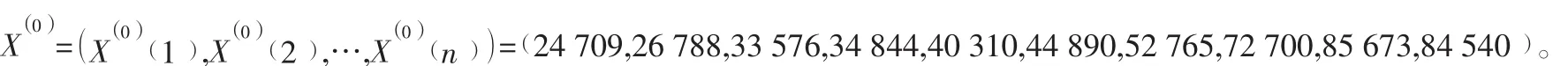
利用线性回归得以得到a,u两个值，a=-0.15444,u=20 477.57,u/a=-132 592。

根据上式可以得到2006～2015年度的预测值，进而可以得到残差和相对误差如表2所示：

从表2可以看到，GM 1,（）1的预测结果基本可以接受，平均误差为5.841%，最大年度误差为9.61%。

2.2 马尔科夫转移矩阵

根据马尔科夫链分析方法经验和实际情况，按照货运量的增幅和灰色预测结果比较，可以划分为5个状态[10]。

E1：呈现极度高估状态，即评估差额与实际货运量的比例在（-∞，-10%）之间。观察表2，2006～2015年并没有这种状态；

表2 2006～2015年GM 1,（）1预测结果 单位：万吨

E2：呈现高估状态，即评估差额与实际货运量的比例在（-10%，-5%）之间，观察表2，2006～2015年中，有3年（2011、2012、2015） 呈现这种状态；

E3：评估较为准确，即评估差额与实际货运量的比例在（-5%，5%）之间，观察表2，2006～2015年中，有4年（2006、2007、2009、2010） 呈现这种状态；

E4：呈现低估状态，即评估差额与实际货运量的比例在（5%，10%）之间，观察表2，2006～2015年中，有3年（2008、2013、2014） 呈现这种状态；

E5：呈现极度低估状态，即评估差额与实际货运量的比例在（10%，+∞）之间，观察表2，2006～2015年中，并没有出现这种状态。

从以上分类中可以得到2006～2015年的状态转移矩阵，如表3所示：

表3 2006～2015年贵州省货运量灰色预测结果马尔科夫状态转移

根据表3，可得到转移矩阵为：

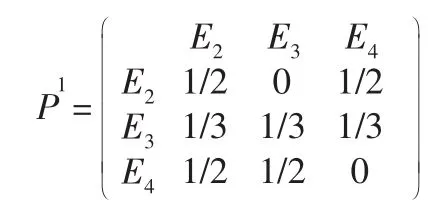
根据马尔科夫的无后效性特点，选取2015年为初始状态，初始向量X0=（0,1,0）,，则2016～2020年的状态向量如表4所示：

表4 2015～2020年贵州省货运量灰色预测结果马尔科夫状态向量

2015年状态向量：X1=（0,1,0 ），2016年状态向量：X1=X0×P=（0.33,0.33,0.33 ），2017年状态向量：X2=X1×P=（0.44,0.28,0.28 ），2018年状态向量：X3=X2×P=（0.45,0.23,0.32 ），2019年状态向量：X4=X3×P=（0.46,0.24,0.30 ），2020年状态向量：X5=X4×P=（0.46,0.23,0.31）。

2.3 GM（ 1,1）预测结果的马尔科夫链改进

根据上面的式子可以得到修正后的灰色预测值，再用它计算出来的精度与灰色GM（ 1,1）模型得到的精度进行比较，确保预测的准确度。对比数据见表5：

通过表5可以得到通过马尔科夫GM（ 1,1）修正过的相对平均误差值为1.654%，比灰色GM（ 1,1）模型的平均误差降低了4.187%，精准度提高了71.7%，数据更为科学准确。通过图1可以清楚看到两种模型与实际值的偏离程度：

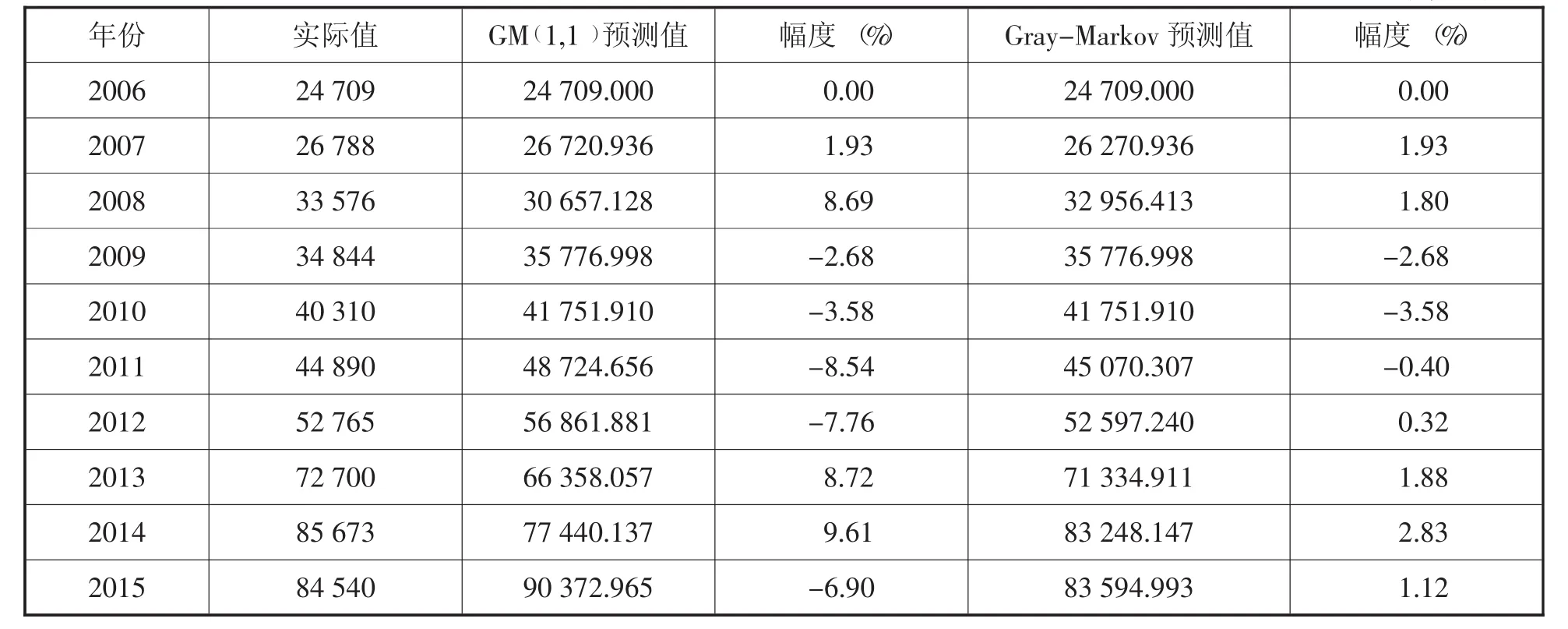
表5 灰色GM（ 1,1）模型与灰色马尔科夫链GM（ 1,1）模型预测结果 单位：万吨

图1 两种预测模型结果对比

2.4 未来5年贵州省货运量预测

观察表6，贵州省的物流量在未来5年中呈现上升趋势，最大的可能概率分布为50%，46%，47%；其次为33%，30%，31%，而且都为低估状态，也就是说未来5年贵州省的实际物流需求量要大于马尔科夫预测值。

3 结论

文中分别应用灰色GM（ 1,1）模型和灰色马尔科夫链GM（ 1,1）模型对贵州省近10年的物流量数据进行建模预测，通过两种方法预测的结果与实际货运量比较，经由马尔科夫修正的灰色GM（ 1,1）模型所得到的数据与实际数据的偏离程度更小，精准度越高。相比于灰色GM（ 1,1）只预测出物流量，灰色马尔科夫链GM（ 1,1）不但可以给出比较准确的预测值，而且还可以求出预测年份的物流量区间以及与之相对应的产生概率。

从预测的数据看，未来5年内贵州省的物流量呈现稳步增长的态势，这表明贵州省的经济发展对于物流的需求量持续上涨，因此政府应该大力布局物流产业，为物流的发展提供政策扶持、资金支持等红利，从而为其他产业的发展提供良好的外部支撑，推动贵州省经济良好健康发展。

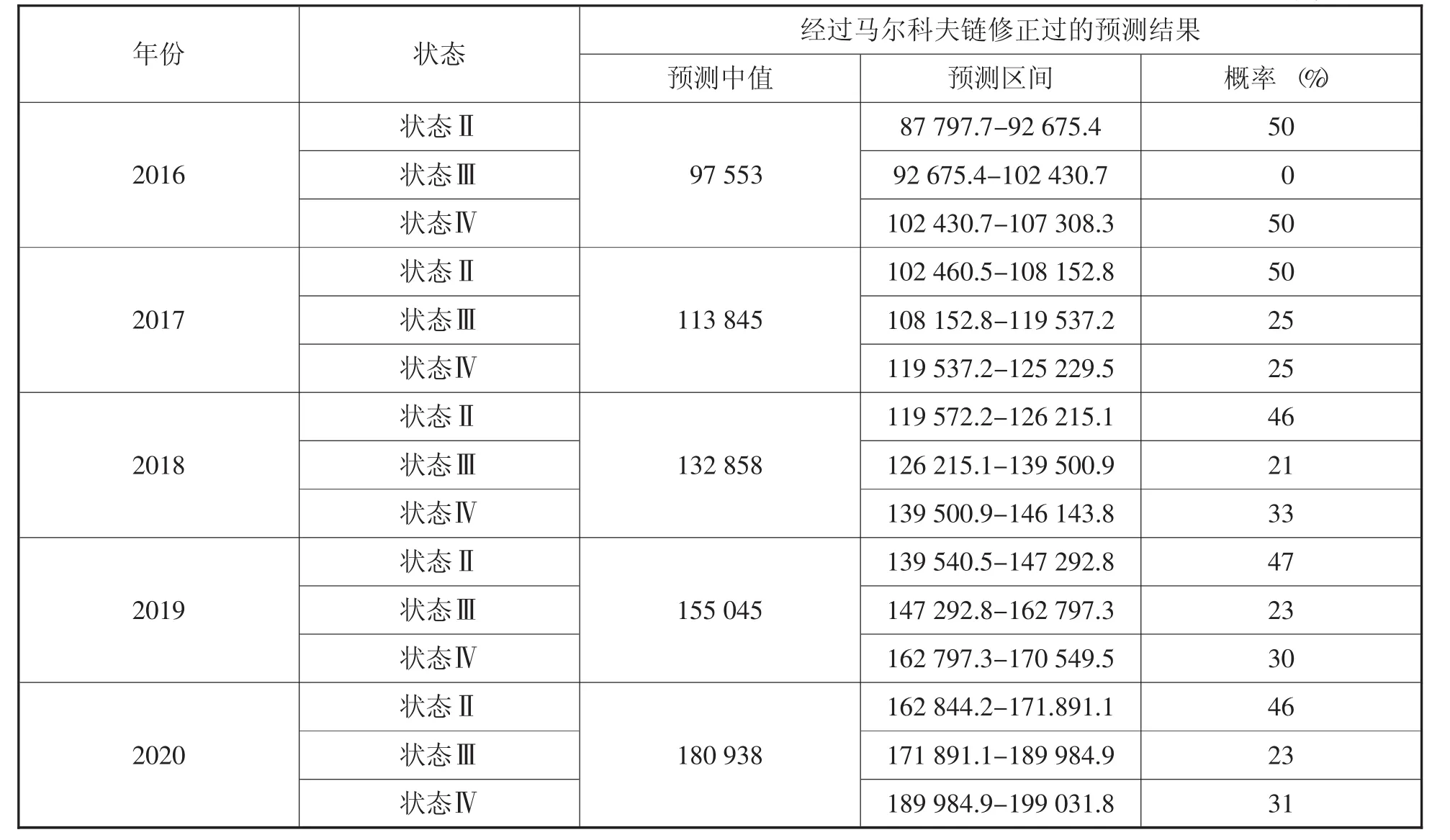
表6 贵州省2016～2020年物流量预测值 单位：万吨