电商物流配送中心选址布局问题研究

王根基，李 莉 （新疆农业大学 交通与物流工程学院，新疆 乌鲁木齐 830052）

0 引言

配送中心选址在整个物流体系中发挥着重要作用，属于物流战略层关注的问题。配送中心的合理选址能够有效降低成本，节约资源，协调生产和消费两个过程，实现物流系统的高效均衡发展，从而提高企业的经济效益[1]。物流配送中心选址问题是物流配送研究的核心问题，关于这方面的研究，常可以看到有学者以运输费率发送率计算运输费用，这与实践并不相吻合[2]。本文考虑了从分段运输关系造成的分段运输成本，以及车辆每日固定成本是总固定成本中重要组成部分的关系，从成本最小化的目标出发构建混合整数非线性规划数学模型，可以更接近实际生活中所遇到的问题，并通过遗传算法求解实际问题。

1 物流配送中心选址模型的建立

1.1 条件假设

为了便于建立配送中心选址模型，假设系统满足如下一些条件：（1）一个需求点仅由一个配送中心供应；（2）配送中心容量可以满足配送需求点的需求量；（3）各需求点的需求量已知；（4）各需求点需求的货物一次运输完成，所有点间运输能力一样；（5）物流中心到每个配送中心的货物分别有一辆车提供运输。

1.2 建立模型

建设区域物流中心J为区域内K个配送中心分配货物，K个配送中心需要满足区域内L个需求点的配送需求。通过基于总成本最小的目标函数来建立模型，总成本包括J点到K点的运输费用，K点到L点的运输费用，建设配送中心的固定成本，以及配送中心周转货物的变动成本。

基于上述假设，建立基于成本最小的配送中心选址模型如下：

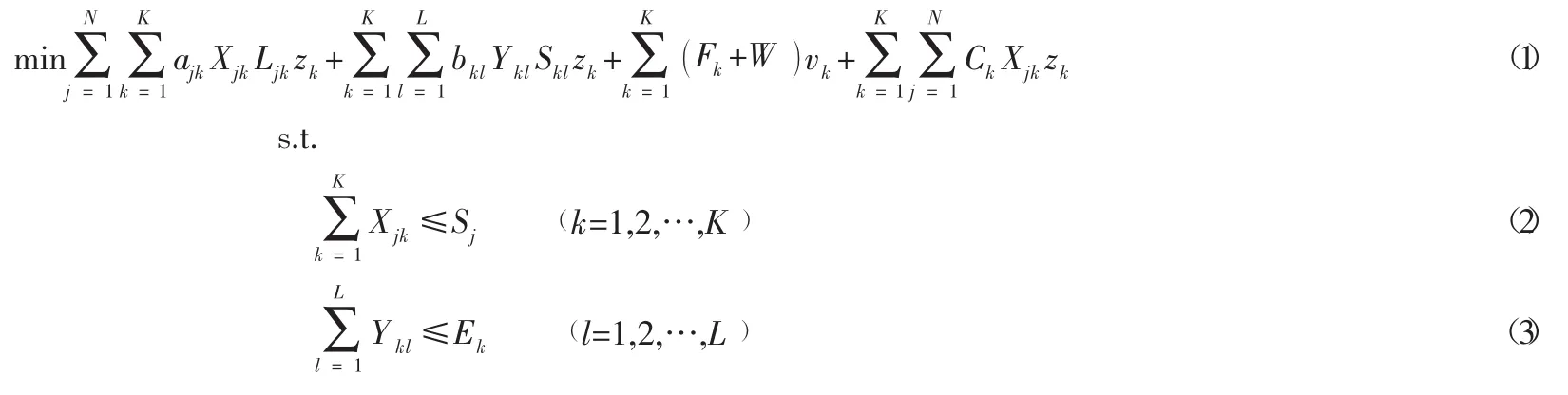
式中：j为物流中心，J为区域物流中心集合，k为配送中心，K为备选配送中心集合，l为需求点，L为需求点集合，Sj为物流中心最大处理能力，Fk为配送中心k的固定成本，W为车辆每日固定成本，Ck为配送中心k周转货物的变动成本，Ek为配送中心k的最大处理能力，ajk为物流中心j到配送中心k的运输费率，bkl为配送中心k到需求点l的运输费率，Xjk为物流中心j到配送中心k的运输量，Ykl为配送中心k到需求点l的运输量，Ljk为物流中心j到配送中心k的距离，Sjk为配送中心k到需求点l的距离，zk,vk为0-1变量。

约束条件说明：式（1）表示目标函数；式（2）表示从区域物流中心发往配送中心的总运量不得超过区域物流中心的最大处理能力；式（3）表示各需求点的总需求量不得超过为其提供配送服务的配送中心的最大处理能力；式（4）表示配送中心的进出货量相等；式（5）表示配送中心总数为4；式（6）zk表示若配送中心k为需求点提供服务则为1，否则为0；vk表示当配送中心k被选中时为1，否则为0。

2 遗传算法

遗传算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象，从任一初始种群出发，通过随机选择、交叉和变异操作，产生一群更适应环境的个体，使群体进化到搜索空间中越来越好的区域，这样一代一代地不断繁衍进化，最后收敛到一群最适应环境的个体，求得问题的最优解[3]。

遗传算法的一般求解过程如下：

（1）编码。将解空间中的解数据从数据形式的表现型到二进制形式基因型的映射成为编码。

（2）生成初始种群。从解空间中随机产生N个初始串结构数据，每一个初始串数据称为一个个体，N个个体构成一个初始种群P（0 ），一般取20～100。

（3）适应度检测评估。适应度函数是用来评价种群中各个个体好坏的标准，是算法演化的驱动力，也是进行自然选择的唯一依据。本文的目标函数是总成本最小，适应度函数为目标函数的倒数。

（4）遗传操作。遗传算法包括三个基本操作：选择、交叉、变异。群体经过选择、交叉、变异运算后得到下一代群体。本文选择运算使用轮盘选择算子，交叉运算使用单电交叉算子，变异运算使用基本位变异算子。

（5）终止条件判断。当运算达到预先设定的代数或测得种群中最优个体性能满足问题约束条件时可终止运算，否则重复步骤（2）、（3）、（4） 直到达到终止条件。

3 实例应用分析

本文以苏宁在乌鲁木齐主城区的城市配送网络为实例。苏宁在乌鲁木齐拥有1个物流中心，承担新疆地区线上订单分拨和线下商品的存储、分拣、调拨等作业。主城区有9家门店作为备选配送中心，从中选取4家门店作为配送中心，承担周边一定范围内中转配送服务。本文将主城区主要街道作为需求点共计43个，便于采用百度地图坐标拾取器采集需求点数据，各需求点的配送需求量来自实地调研数据，并将临近小规模需求点货量进行合并。配送中心备选点数据如表1所示：

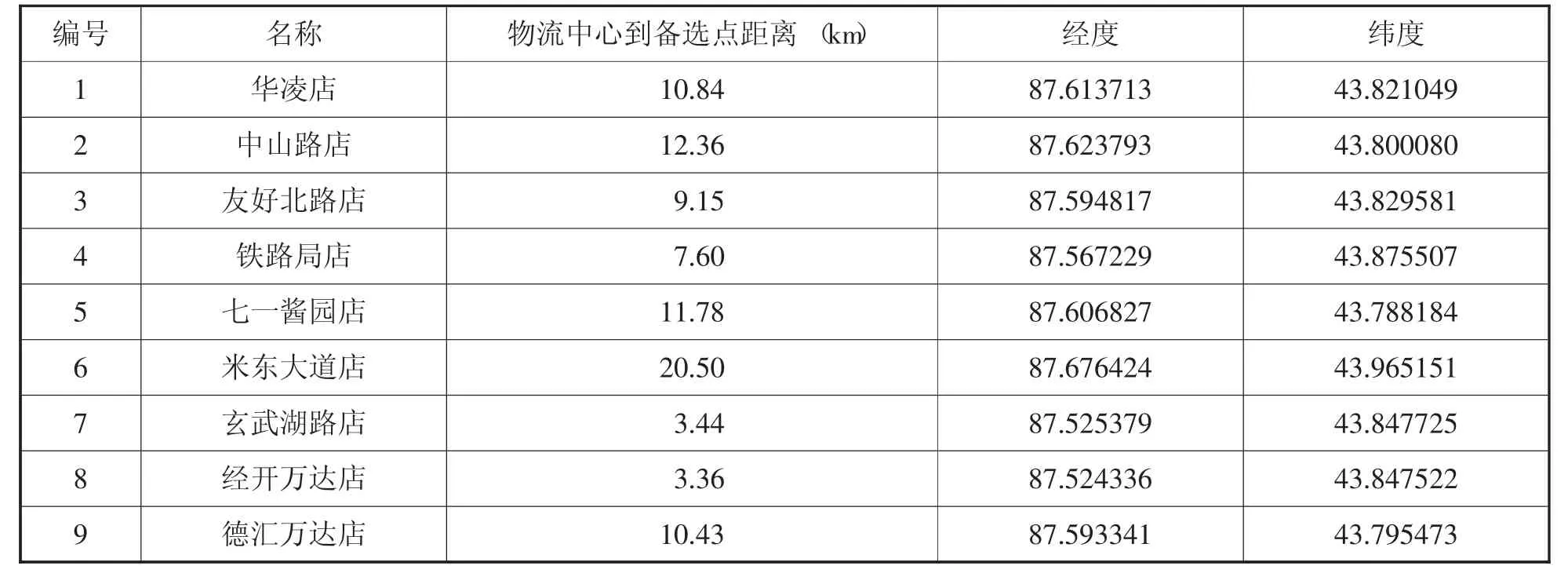
表1 配送中心备选点数据

根据在苏宁实地调研得知，以4.6米箱货车型为例，车辆每日折旧费67元/天，保险16.7元/天，司机工资150/天，得到每日车辆固定成本233元/天，总共配有4辆车，每日车辆总固定成本为932元。配送中心面积为50～70平方米，租赁费用由于地区租金差异为3.5～5元/天·平方米，配送中心每日最大处理能力为800个包裹，配送中心每天的固定费用为1 000元/天，从物流中心到配送中心的费用为0.4元/公里·件，从配送中心到需求点的配送费用为0.8元/件·公里，配送中心可变费用为2元/件（包括中转费用，快递员提成费用等）。

在MATLAB2016a上运行设计的程序，进行计算实验，算法采用以下参数可以得到较好的性能，其中初始种群大小（NIND）为200，遗传代数 （MAXGEN）为500，交叉概率（Pc）为0.8，变异概率 （Pm）为0.1，代沟 （GGAP）为0.9。程序运行20次后得到的结果如图1、表2所示。

如图1所示，运行20次程序产生的4种不同结果中，第二种和第三种方案的成本相接近且远低于第一种和第四种方案，所以再根据程序运行结果时产生的总成本进行比较。

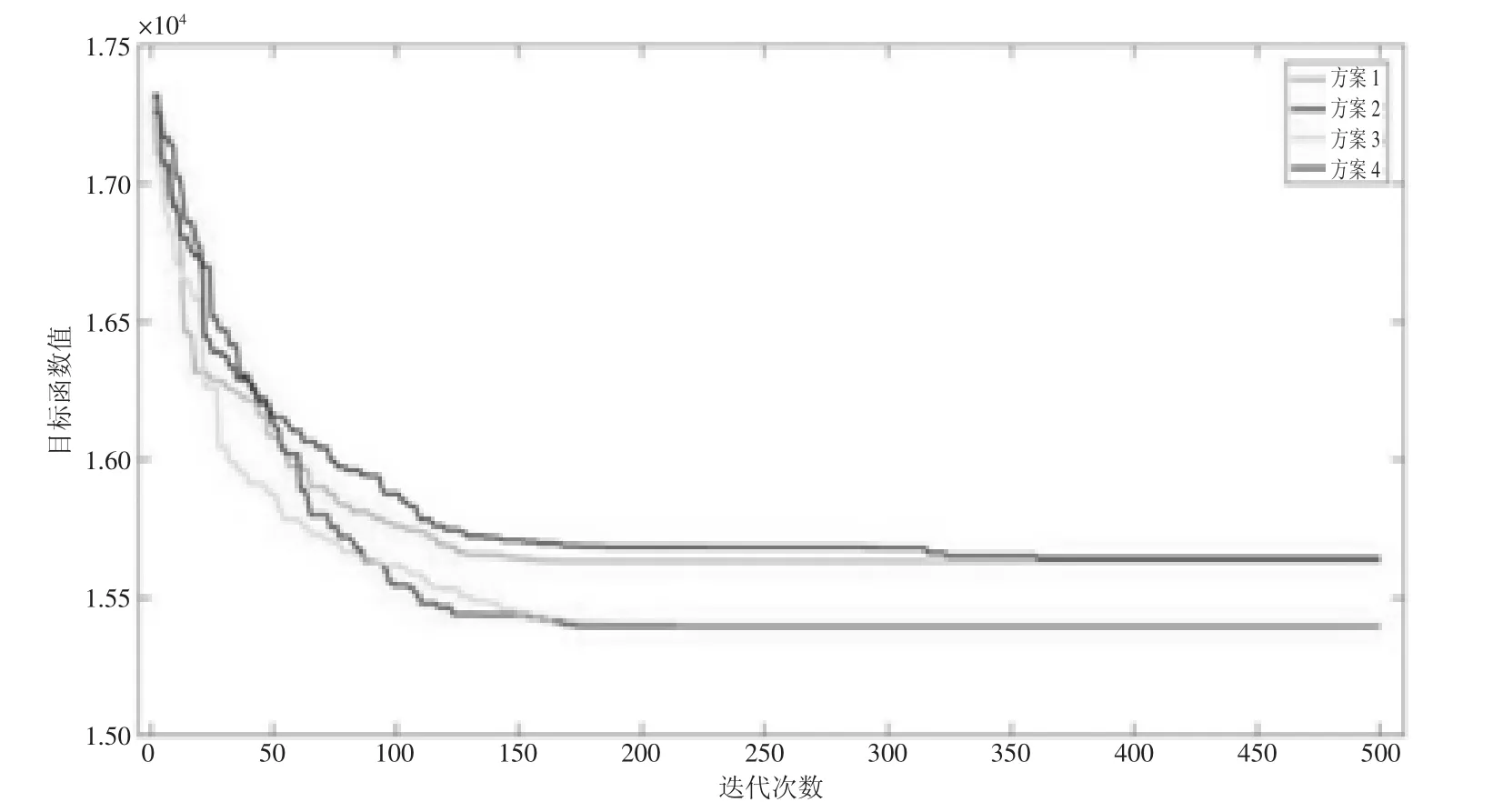
图1 目标函数与遗传代数的关系

如表2所示，表2中列出了4种方案的配送中心开放情况以及对应的物流总成本，其中第二种方案当选择点7、3、9、4为配送中心时的物流总成本为15 395元，比第三种方案的总成本略低，为4种方案的最低成本，所以选择第二种配送方案为最佳方案。

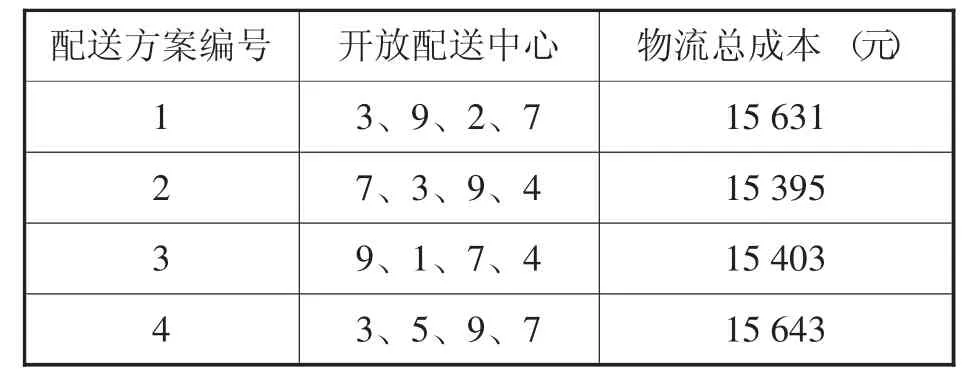
表2 配送方案

用MATLAB2016a对模型进行求解的同时，可得到其对应的需求点分配方案。如表3所示，第二种方案的需求点分配情况，运行结果为：选中备选点3、4、7、9，其中需求点分配方案为：配送中心 3 为 11、12、17、18、19、23、25、32、36、37、38、40、41 需求点提供配送服务，配送中心4为26、27、30、31、33、34、39、42、43需求点提供配送服务，配送中心7为21、24、28、29、35需求点提供配送服务，配送中心9为1、2、3、4、5、6、7、8、9、10、13、14、15、16、20、22需求点提供配送服务。

表3 最佳需求点配送方案

4 结论

通过对苏宁在乌鲁木齐市主城区的配送网络为例，对模型算法进行了实例分析，结果表明本文构造的基于成本最优的目的提出了考虑不同层级设施的运输关系以及车辆固定成本问题的配送中心选址模型和算法可以快速确定电商物流配送中心的位置和最小成本，以及需求点分配方案。但是，由于本文算例只有一个物流中心，所以今后的研究中可以通过多物流中心的算例进行验证和优化。此外，也可在算法方面加以优化改进，期望可以得到更加完善的模型算法。