例谈关于解斜三角形的试题类型
杨宜龙
(河北省石家庄西山学校 050000)
下面本文对该知识点在高考中的考查进行分类解析,供同学们参考:
一、已知三角形的三个独立条件(不含已知三个角的情况),求解三角形
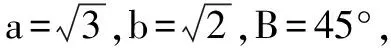
分析已知三角形的两边和其一边的对角这种类型题目,是同学们在学习过程中感到最困难的一种习题,这种习题可以利用正弦定理和余弦定理进行解决.


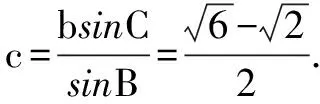
点评用正弦定理解题,往往通过大边对大角这一性质判断解的个数;而用余弦定理解题,往往通过根的正负或Δ来判断解的个数.
二、判断三角形的形状
例2 在△ABC中,已知(a2+b2)sin(A-B)=(a2-b2)sinC,判断三角形的形状.
分析判断三角形的形状通常是根据正弦定理或余弦定理将已知条件变换成只含边或角的式子,再通过边或角的关系判断出三角形的形状.
解将原式转化为
(a2+b2)(sinAcosB-cosAsinB)
=(a2-b2)(sinAcosB+cosAsinB),
即a2sinBcosA=b2sinAcosB.
由正弦定理得acosA=bcosB,
∴a2(b2+c2-a2)=b2(a2+c2-b2),整理得
(a4-b4)-(a2c2-b2c2)=0,
(a2-c2)(a2+b2-c2)=0.
∴a=b或a2+b2=c2.
∴△ABC是等腰三角形或直角三角形.
三、三角形中恒等式的化简与证明



点评证明三角形中的边角等式的主要依据是正弦定理、余弦定理以及三角式的恒等变形,运用正弦定理、余弦定理实现边与角之间的相互转换.
四、三角形中的求值问题
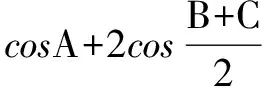
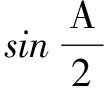

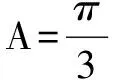
点评本题考查诱导公式、二倍角公式的应用,利用特殊三角函数值求角,二次函数求最值用到了配方法.
五、利用斜三角形解决实际应用问题
近几年来的高考应用性问题不难看出,试题从实际出发提供公平的背景,设计新颖,这就要求我们关注生活、科技发展等各个方面,不断追求新知,学会将实际问题抽象为数学问题,需要提高我们运用数学知识解决实际问题的能力.

例5 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待救援.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1°)?

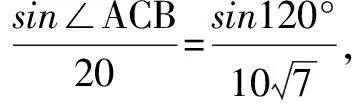
∵∠ACB<90°,∴∠ACB≈41°.
所以,乙船应朝北偏东71°方向前往B处救援.
点评本题考查了解三角形中的正弦、余弦定理,函数值与角的互化及运算能力.考查学生对数学知识的应用及数形结合的能力,该题型是高考常考题型,在解此类题目时不要忘记方位角的定义.

