基于四方博弈模型的PPP项目风险分担研究

孟枫平，刘淑雯

（安徽农业大学经济管理学院，安徽合肥，230036）

PPP（Public—Private—Partnership）模式，是指政府引进社会资本共同建造基础设施，双方以共享利益、共担风险为合作基础，通过签署合同来明确双方的权利和义务，使项目参与方达到比己方单独行动更为有利的结果。2014年颁布的《政府和社会资本合作模式操作指南（试行）》表明PPP项目的中国化模式已初步形成，也预示着PPP项目在我国进入了快速发展阶段。根据全国PPP综合信息平台项目库发布的数据显示，截至2017年末，全国PPP项目共14424个，总投资额高达18万亿元。由于PPP项目具有周期长、投资大、风险高的特点，涉及政府部门、私人投资者、项目公司、金融机构等多个参与方，因此，在各参与方之间合理分配风险是项目成功的一个关键步骤。

一、文献综述

目前，国内外对PPP风险的研究角度比较多元。国外的学者对PPP风险的研究较为成熟。Li B等运用统计分析法，根据英国PPP项目的数据确定了风险分担［1］；NG&Loosemore根据澳大利亚的项目数据，分析政府与私人部门之间的风险分担方案［2］。相比较而言，国内的PPP项目研究总体还处于探索阶段。周鑫构建了政府部门和私人部门双方讨价还价模型，使用贴现率来确定风险分担的比例［3］；林媛等采用模糊逻辑方法对PPP项目进行了风险分配［4］；叶秀东利用多目标规划方法找到最佳风险分担方案，构建项目风险评价指标体系，运用层次分析法与综合评价法确定项目的风险水平［5］；李林根据参与方地位是否对称的情况构建了政府部门与私人企业的讨价还价博弈模型［6］；李妍运用不完全信息条件下讨价还价博弈理论，根据PPP项目中参与方轮流出价的不同次序，构建了不同出价顺序的风险分担模型，且得出了政府与社会资本需要承担的风险比例［7］。

国内外学者研究风险分担的方法主要分为五类：一是主观性较强的调查问卷方法；二是通过项目数据构建数学模型的方法，有限适用；三是层次分析法，由于PPP项目风险分担的指标因素过多，所以采用该方法会造成数据统计量大且各个因素之间的权重难以确定；四是案例分析法，针对典型案例进行分析，但对其他的PPP风险分担只能起到借鉴作用，不具有普适性；五是博弈论方法，通过考虑参与者的预测行为与实际行为，研究各参与者的优化策略，是定性与定量的结合，又可进一步分为静态博弈与动态博弈，其中动态博弈更能够反映PPP项目参与方在整个谈判过程中对风险分配的讨价还价过程，并且由于PPP项目中各参与方的地位是不对称的，策略的选择有先后之分，而次序的不同又会导致不同的结果。基于此，本文选择运用动态博弈模型研究PPP项目的风险分担，又由于现有的研究仅考虑了政府部门和私人部门两个参与方，并未考虑PPP项目参与方构成的多样性，本文拟建立政府部门、投资人、承包商、银行四方的讨价还价博弈模型，计算各自需要承担的风险比例。

二、博弈过程

PPP项目参与方包括政府部门、投资人、承包商、银行、监理单位担保方及最终使用者，但其中政府部门、投资人、承包商、银行才是PPP项目中的重要参与者（见图1）。四个参与方对PPP项目各类风险进行合理分配是关系项目成功的重要因素。在PPP项目的四个参与者讨价还价过程中，为了实现己方利益最大化，往往会暂时地选择自发性的联合，此类行为称之为联盟。由于联盟后对另一方的威慑力大大增强，可以使联盟分担更少的风险，得到的风险最后在联盟内部进行分配。

在现实中，政府部门相比较其他三方属于强势地位，所以由纯投资商、承包商与银行合作成立“联盟1”，与政府部门谈判，进行风险分担，按照讨价还价模型轮流出价，最终达到均衡，然后将“联盟1”的风险在投资人、承包商、银行三方之间进行分配，最终合理分配四方各自需要承担的风险比例。

根据参与者掌握的信息程度，可以将博弈划分为完全信息博弈与不完全信息博弈，前者是指参与者充分掌握对方的博弈信息，后者则意味着彼此不能掌握对方的全部博弈信息。

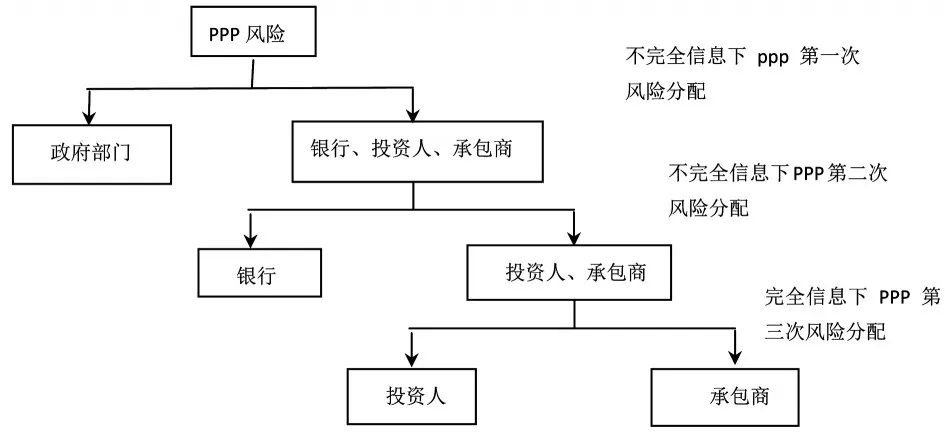
图1 PPP项目风险分担的四方博弈模型

三、不完全信息条件下风险的第一次分配

采用讨价还价博弈模型，纯投资方、承包商、银行相对于政府部门处于弱势地位，所以投资人、承包商、银行为了获得己方利益最大化，会合作组成“联盟1”与政府部门讨价还价。

（一）基本假设

假设1 政府与“联盟1”均是个体理性人，以个体自身利益最大化为根本目标且双方希望最终谈判成功。

假设2 政府与联盟1间的信息是不对称的。

假设3 风险是相互独立的，彼此之间没有关联且初始值都为1。

（二）模型参数的设定

1.谈判损耗系数β

在政府与“联盟1”进行讨价还价谈判的过程中，最重要的就是谈判损耗系数β（β＞1）。谈判损耗系数β指的是在谈判过程中双方都需要承担并且必然会发生的谈判成本，主要包括时间成本、信息获取成本等交易成本。根据实际PPP项目谈判中的情况，政府部门在PPP项目中占主导地位，所以博弈中政府需要承担的成本低于“联盟1”的谈判成本。

2.政府部门强势的概率

在博弈过程中，政府将以概率为p1的可能性强迫对方接受己方的风险量；以概率p2的可能性不威慑“联盟1”承担更多风险。（p1+p2=1）

3.风险转移值

政府以概率为p1的可能性强迫“联盟1”接受己方的风险量为∂，且风险转移值肯定小于政府自身承受的风险比例ki，故0≤∂≤ki＜1。

（三）模型的建立

在讨价还价博弈过程中占据优势地位的一方优先出价，所以由政府先出价，“联盟1”根据对方提出的分配方案进行选择，接受就结束谈判，拒绝则继续下一轮谈判。

1.第一轮谈判

政府提出己方可承担风险k1，则“联盟1”需要分担风险为1-k1。

（1）政府以概率为p1的可能性强迫对方接受属于自己的风险量∂的情况下，政府需要承担的风险G'1和“联盟1”应承担的风险U'1分别为：

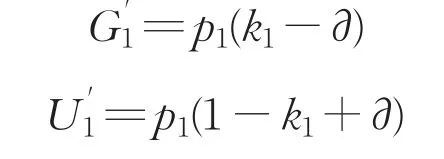
（2）政府以1-p1的概率不强迫“联盟1”接受属于自己风险量时，政府需要承担的风险G''1和“联盟1”应承担的风险U''1分别为

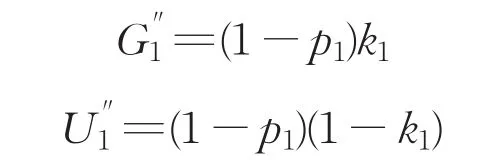
则第一轮政府部门和“联盟1”承担的风险G1、U1分别为：

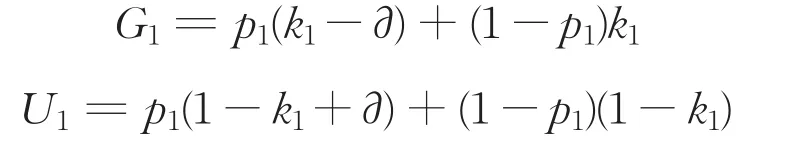
若“联盟1”拒绝承担该风险比例，则谈判自动进入第二轮。

2.第二轮谈判

第二轮谈判由“联盟1”提出方案，政府承担风险比例k2，则“联盟1”承担风险比例为1-k2，政府的谈判成本（β1），“联盟1”谈判损耗系数（β2）。同理，政府部门会以概率为p1的可能性强迫对方接受属于自己的风险量∂。

综上可得出：

政府承担风险：

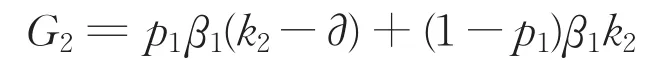
“联盟1”承担风险：

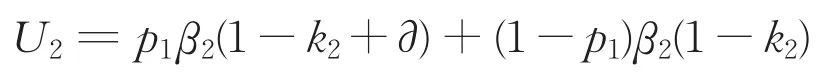
如果政府不同意“联盟1”提出的分配比例，则结束第二轮谈判，进入第三轮谈判。

3.第三轮谈判

第三轮谈判由政府部门先出价，提出承担风险比例k3，则“联盟1”承担风险比例为1-k3，政府部门的谈判成本（β1），“联盟1”谈判损耗系数（β2）。

同理可得：

政府承担风险：

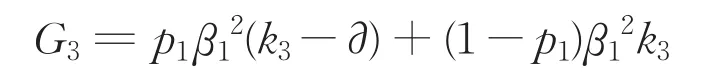
“联盟1”承担风险：

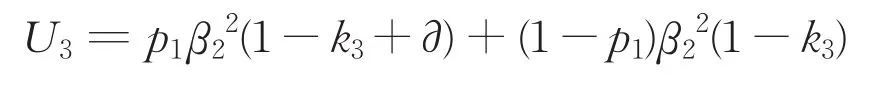
若政府与联盟1都无法接受对方提出的分配方案，则博弈谈判在理论上会无限循环下去，直到双方达成共识。

（四）模型的求解

该模型为非完全信息条件下的讨价还价博弈模型，结合海尼萨转换理论可知

本模型应设立一个逆推基点来求解，设立的基点在任何回合结果都相同，k1=k3。本文选择有限期中的第三轮谈判作为逆推基点。

若第二轮“联盟1”提出的方案使得政府承担的风险G2大于第三轮的风险G3，则政府会拒绝第二轮的谈判结果，那么就需要进入第三轮谈判。但是每进行一次谈判，“联盟1”都会承担谈判损耗，且联盟的谈判损耗（β2）大于政府部门谈判损耗系数（β1），所以“联盟1”为了避免增加自己的谈判损耗，会在第二轮提出的分配方案里使得自己承担的风险期望值最小且政府部门在第二轮的风险G2不大于第三轮的风险G3，即

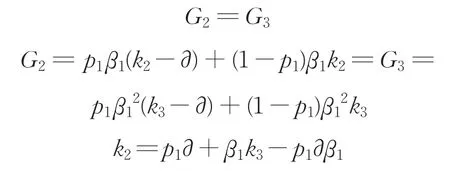
那么“联盟1”的第二轮与第三轮承担的风险期望值分别是：

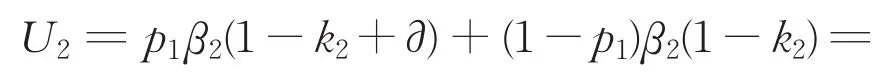
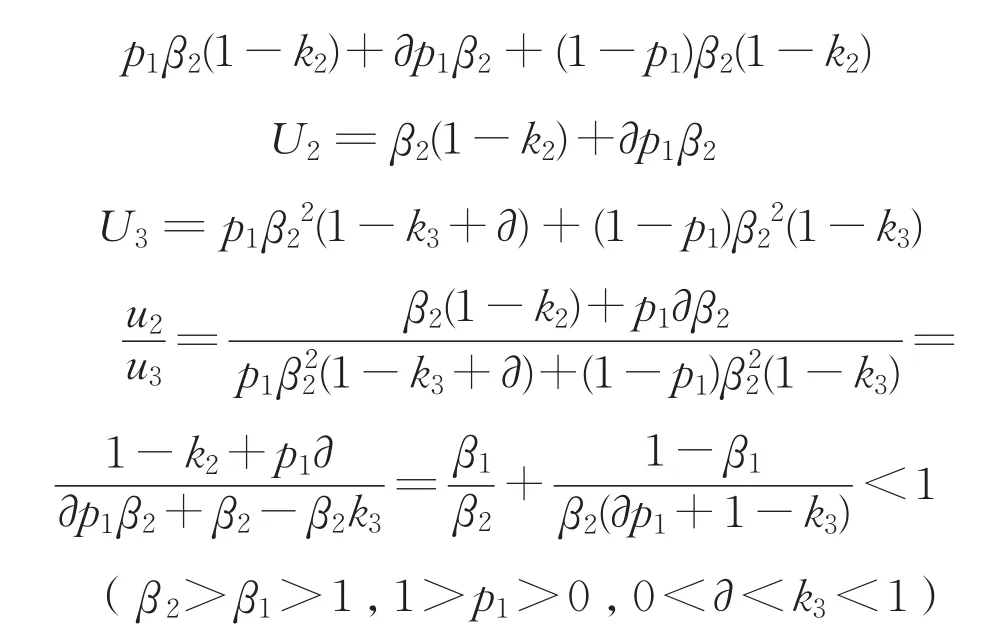
根据上式得知U2＜U3，也就是“联盟1”在第二轮的风险比例U2比第三轮的风险比例U3还要小，所以“联盟1”与政府部门都不会考虑将谈判持续至第三轮。

接下来再考虑政府部门与“联盟1”博弈的第一轮。如果政府部门在第一轮提出的风险分配比例使得“联盟1”在第一轮承担的U1大于第二轮承担的U2，则“联盟1”在第一轮就会拒绝政府部门的分配方案，谈判就进入第二轮。因为每进行一次谈判，政府部门都会增加谈判损耗，政府部门也不希望谈判继续第二轮，因此政府部门在第一轮提议的风险分配方案应是：在自己第一轮承担风险G1最小的基础上，让“联盟1”第一轮承担的U1不大于其在第二轮承担的U2，则政府部门在第一轮的最优策略是：

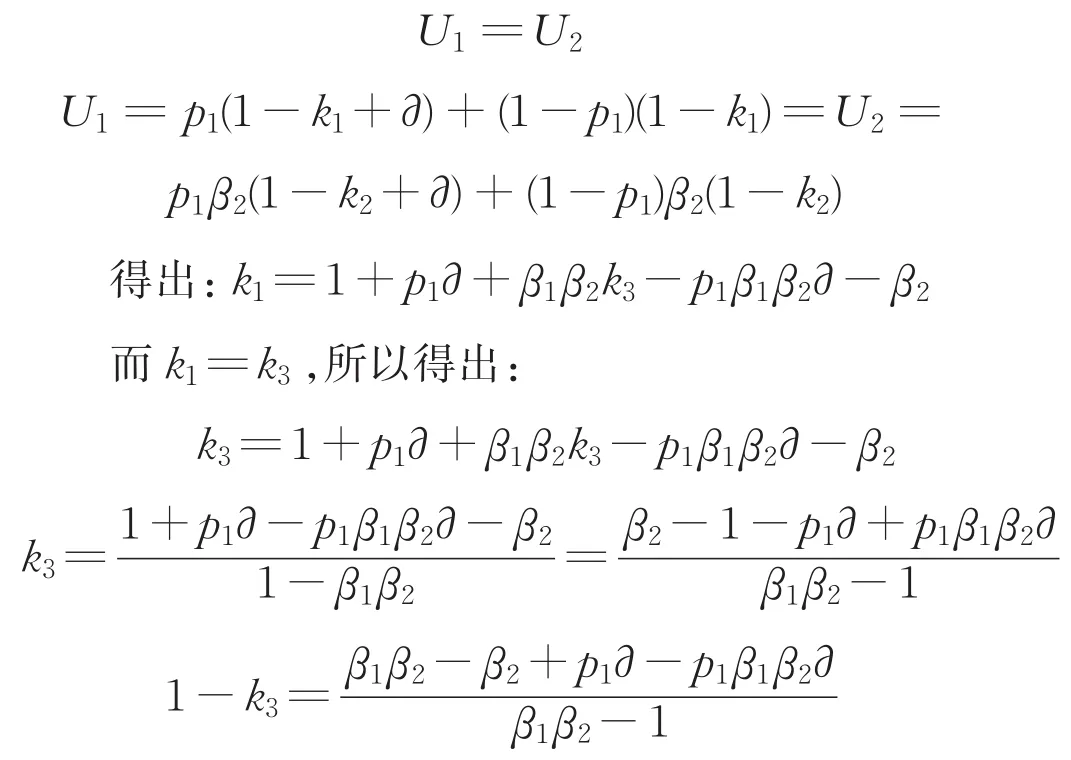
则得出政府部门与“联盟1”承担风险的均衡比例为：

政府部门：

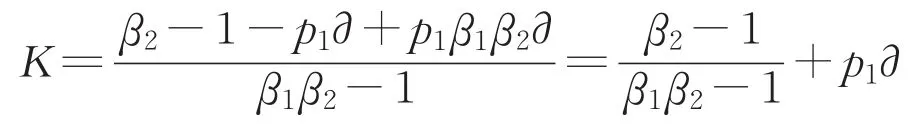
“联盟1”：

政府和“联盟1”承担的名义风险比例分别为K、1-K。其中p1∂为政府利用优势地位强势转移给“联盟1”的风险份额。实际上，政府承担的风险份额为K-p1∂，“联盟1”承担的风险份额为1-K+p1∂。

四、不完全信息条件下风险的第二次分配

由于银行相对比投资人与承包商在PPP项目中具有优势地位，所以由投资人、承包商组建成“联盟2”，与银行讨价还价，建立讨价还价博弈模型，得出合理的风险分担比例。

（一）基本假设

假设1 银行与“联盟2”均是个体理性人，即双方的决策和行为是以个体自身利益最大化为根本目标的，并且双方希望最终谈判成功。

假设2 银行与“联盟2”彼此不能完全了解对方的风险情况。

假设3 风险是相互独立的，彼此之间无关联。

（二）模型参数的设定

1.谈判损耗系数β

在实际PPP项目谈判中，银行在“联盟2”中占主导地位，所以每进行一次博弈银行需要承担的谈判成本都会低于“联盟1”的谈判成本，即银行谈判损耗系数（β1'）小于“联盟2”谈判损耗系数（β2'）

2.银行部门强势的概率

银行将以概率为q1的可能性利用其强势地位迫使对方接受属于自己的风险量。

3.风险转移值

银行的风险转移值取 ∂'，且0≤ ∂'≤ηi＜γ＜1。

（三）模型的构建

该模型由占据优势地位的银行先出价，“联盟2”观察银行的行为后再选择，

接受就结束谈判，拒绝则继续下一轮谈判。对于某种风险i，银行、投资人与承包商共同承担的风险比例为γ，0＜γ＜1且γ=1-K+P1∂（第一次风险分配时“联盟1”应承担的风险比例），银行承担的风险比例为ηi，则“联盟2”承担的风险为γ-ηi，双方就ηi讨价还价。

1.第一轮谈判

银行先出价，提出己方风险η1，则“联盟2”风险量为γ-η1

（1）银行以概率为q1的可能性强迫对方接受属于自己的风险量∂'的情况下，银行需要承担的风险B'1和“联盟2”应承担的风险S'1分别为：

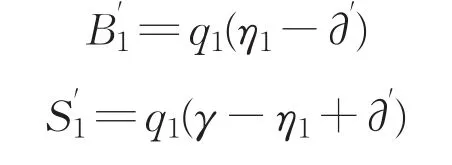
（2）银行以1-q1的概率不强迫“联盟2”接受属于自己风险量时，银行需要承担的风险B''1和“联盟2”应承担的风险S''1分别为

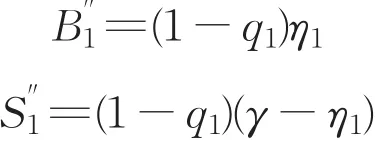
则第一轮银行和“联盟2”承担的风险B1、S1分别为：

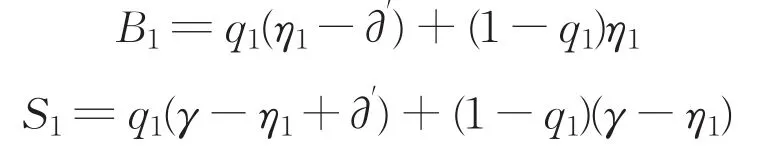
如果“联盟2”拒绝银行在该轮谈判提出的风险分配方案，则继续第二轮谈判。

2.第二轮谈判

“联盟2”拒绝银行的第一轮提出的风险分担比例，则第二轮由“联盟2”出价，提出银行承担风险比例η2，则“联盟2”承担风险比例为γ-η2，银行的谈判成本（β1'），“联盟2”谈判损耗系数（β2'）。则同理可得出第二轮中，银行和“联盟2”承担的风险B'2、S'2分别为：

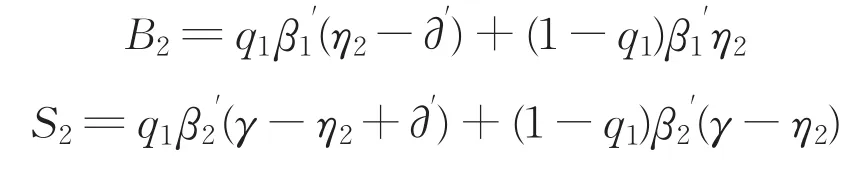
如果银行拒绝“联盟2”提出的风险分配方案，则第二轮谈判结束，进入第三轮谈判。

3.第三轮谈判

第三轮由银行先出价，提出承担风险比例η3，则“联盟2”承担风险比例为γ-η3，银行的谈判成本（β1'），“联盟2”谈判损耗系数（β2'）。同理可得最后银行应承担的风险B3与“联盟2”以承担的风险S3分别为：

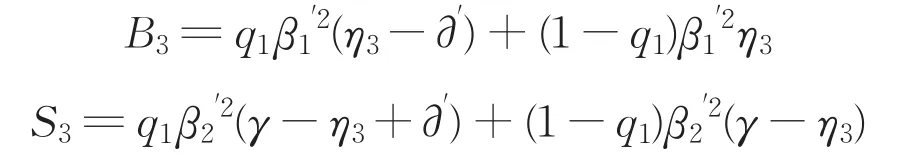
由此可知，如果银行与“联盟2”在每一轮谈判中都无法达到共识，则谈判无限循环，直至谈判双方都同意最终的分配方案。

（四）模型的求解

该模型与上个模型一样都为非完全信息条件下无限回合的讨价还价博弈模型，结合海尼萨转换理论可知，可以设立一个逆推基点来求解，设立的基点在任何回合，结果都相同，即η1=η3。本模型选择有限期中的第三轮作为逆推基点。

如果第二轮“联盟2”提出的分配比例使得银行承担的风险期望B2大于第三轮的B3，则银行会拒绝第二轮的谈判结果，那么就继续第三轮博弈谈判。由于每进行一次谈判，“联盟2”都会承担谈判损耗，并且“联盟2”的谈判损耗（β2'）大于银行谈判损耗系数（β1'），所以“联盟2”为了避免谈判回合的增加而导致谈判损耗的增加，会在第二轮提出的风险分担比例中，使得自己承担的风险期望值最小且银行在第二轮的风险期望B2不大于第三轮的B3，即

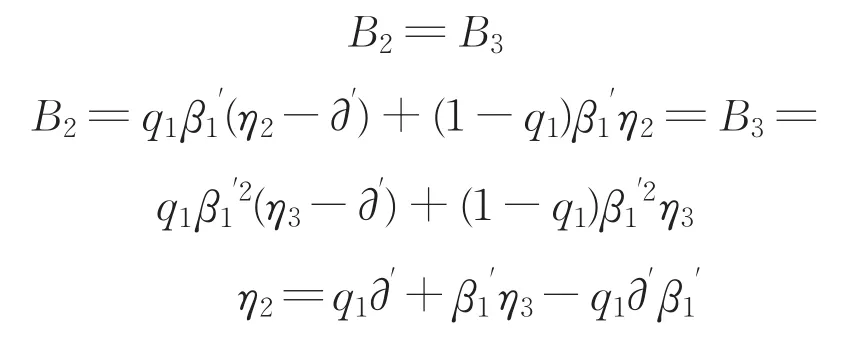
那么“联盟1”的第二轮与第三轮承担的风险期望值分别是：

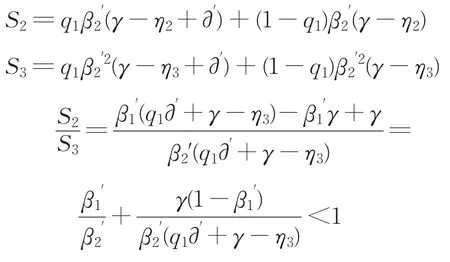
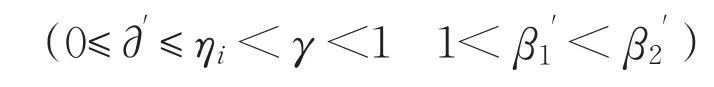
根据上式得知S2＜S3，所以“联盟2”与银行都不会考虑将谈判持续至第三轮。

再考虑银行与“联盟2”谈判的第一轮。如果银行在第一轮谈判中提出的分配方案使得“联盟2”在第一轮的风险期望值S1大于第二轮的风险期望值S2，则“联盟2”在第一轮就会拒绝银行的分配方案，谈判就持续至第二轮，由于谈判有损耗，所以银行也不希望谈判继续第二轮。因此银行在第一轮提议的风险分配方案应是：在自己第一轮承担风险期望值B1最小的基础上，让“联盟2”第一轮承担的风险期望值S1不大于其在第二轮承担的风险期望值S2，则银行在第一轮的最优策略是：

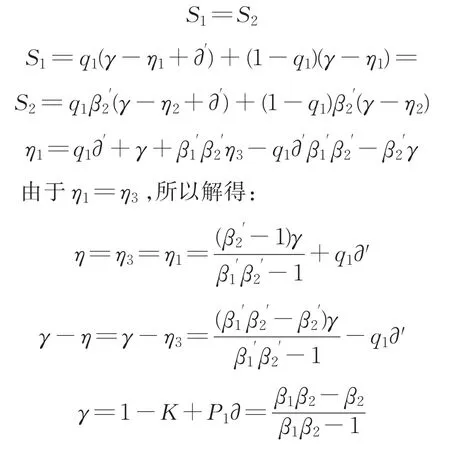
所以银行与“联盟2”承担的风险比例为：

银行：

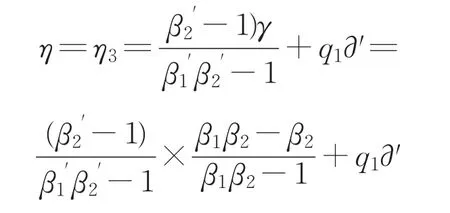
“联盟2”：

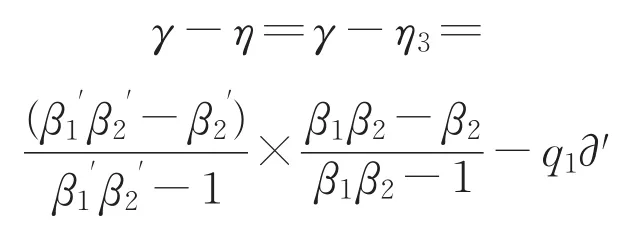
则可得出，银行和“联盟2”针对某一特定的风险承担的名义风险比例分别为η、γ-η。其中q1∂'为银行利用优势地位强势转移给“联盟2”的风险份额。实际上，银行承担的风险份额为ηq1∂'，“联盟2”承担的风险份额为γ-η+q1∂'。

五、完全信息条件下风险的第三次分配

根据“联盟2”应当承担的风险份额，本文将进行风险在“联盟2”内部的风险分配。由于投资人与承包商都属于企业，对PPP项目的环境了解情况与了解渠道都相同，信息是对称的，所以投资人与承包商之间风险分配是基于完全信息条件下的讨价还价模型。

（一）基本假设

假设1 投资人与承包商均以自身利益最大化为根本目标，且双方希望最终谈判成功。

假设2 投资人与承包商对对方的信息都是完全掌握的。

假设3 风险是相互独立的。

假设4 对于某种风险i，投资人与承包商共同承担的风险比例为δ，0＜δ＜1且δ=γ-η+P1∂'（第二次风险分配时“联盟2”应承担的风险比例），投资人承担的风险比例为λi，则承包商承担的风险为δ-λi，双方就λi讨价还价。

（二）模型的构建

该模型由于投资人占据主动地位，所以投资人先出价，提出承担风险比例λ1，则承包商承担风险比例为δ-λ1。投资人利用自己的优势地位强迫对方接受属于自己的风险量∂''的情况下，投资人需要承担的风险I1和承包商应承担的风险C1分别为：

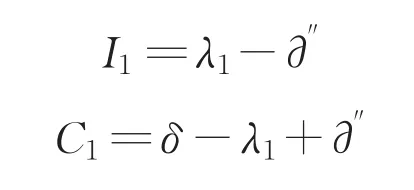
承包商接受投资人在该轮的分配意见，谈判就直接结束，反之进入下一轮。

同理可得出，第二轮投资人与承包商承担的风险为：

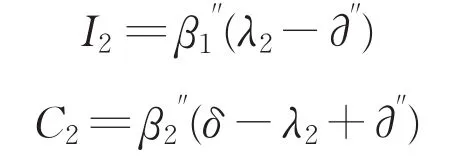
第三轮投资人与承包商承担的风险为：

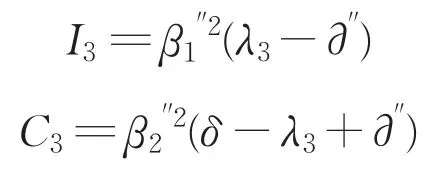
（三）模型的求解

该模型为完全信息条件下无限回合的讨价还价博弈模型。本模型选择有限期中的第三轮为逆推基点。如果第二轮承包商提出的方案使得投资人承担的风险I2大于第三轮的I3，则投资人会拒绝第二轮的谈判结果，那么就不得不进入第三轮博弈谈判。因为每进行一次谈判双方都会承担谈判损耗，并且实际操作中，承包商的谈判损耗（β2''）小于投资人谈判损耗系数（β1''）。所以承包商为了避免谈判次数增加而导致谈判损耗的增加，会在第二轮提出的风险分担比例中，使得自己承担的风险期望值最小且投资人在第二轮的风险期望I2不大于第三轮的风险期望I3，则投资人的最优策略为：

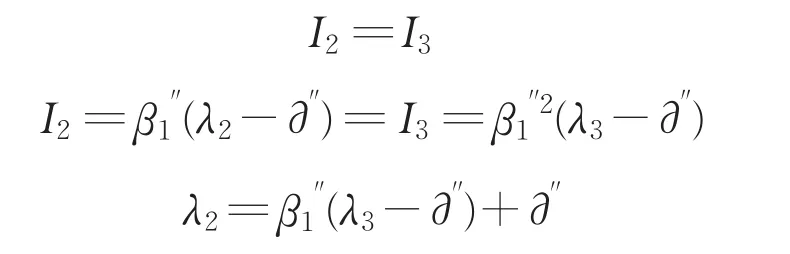
得出承包商在第二轮承担的风险为：

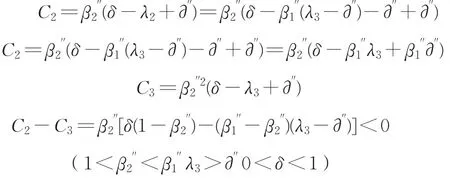
现在逆推到第一轮，如果投资人在第一轮提出的方案使得承包商在第一轮承担的风险C1大于第二轮的C2，则承包商在第一轮就会拒绝投资人的分配方案，谈判就进入第二轮，由于1＜β2''＜β1''，所以投资人也不希望谈判继续第二轮。因此投资人在第一轮提议的风险分配方案应是：在自己第一轮承担风险期望值I1最小的基础上，让承包商第一轮承担的风险C1不大于其在第二轮的C2，则投资人在第一轮的最优策略是：

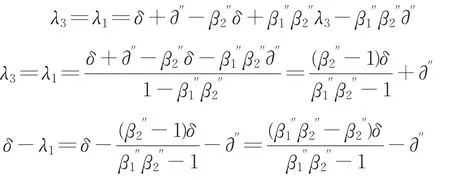
则可得出，投资人和承包商针对某一特定的风险承担的名义风险比例分别为：

其中∂''为投资人利用行业优势地位强势转移给承包商的风险份额。实际上，投资人和承包商针对某一特定的风险承担的名义风险比例分别为：

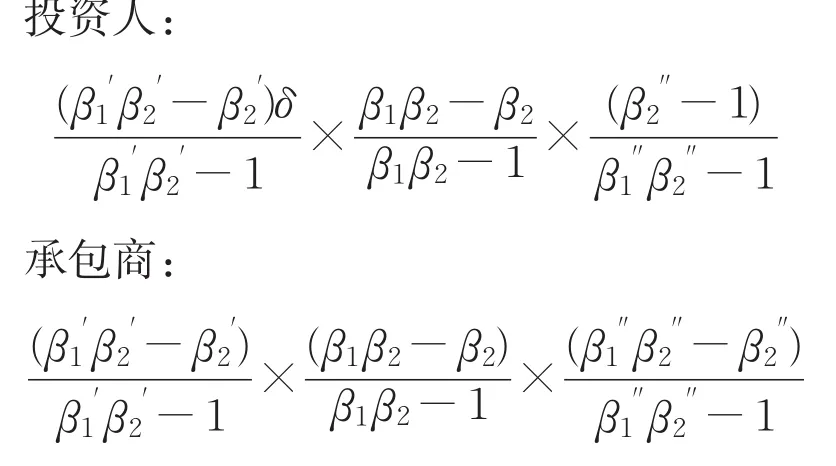
通过上述模型的建立、分析及求解，可知，政府、银行、投资人、承包商四者分配的风险比例与谈判损耗系数β（β＞1）相关。四个参与方实际分担的风险比例分别为：

六、结论及对策建议

（一）结论

本文的模型分析结果表明，PPP项目各方分配的风险比例与谈判损耗系数β有关。根据得出的实际分配的风险比例来看，只有当某方谈判损耗系数β变大，其他参与方的谈判损耗系数不变时，才可以减少该方实际分配的风险比例。而谈判损耗系数β增大有两种途径，一是花费时间跟人力、物力去准备充分的谈判资料，尽可能了解对方的信息与策略；二是谈判次数增多，叠加多次谈判成本。根据调查可知，第一种途径可以有效减少己方的风险比例，第二种途径并不能使得风险在四个参与方中进行最优化的分配，并且增加了不必要的成本。因此，模型分析结果提示，PPP项目中四个参与方若想降低己方的风险比例，可通过花费更多成本去了解对方的信息与谈判策略，并减少谈判次数。

（二）对策建议

在我国，政府部门长期处于强势地位，社会资本处于弱势地位。在PPP项目中，只有合理分配项目风险，保障社会资本的权益，才能提高社会资本进入PPP领域的积极性。因此，本文着重就减少社会资本风险比例提出建议。一是建议社会资本与弱势参与方结成同盟。社会资本投资人在第一轮风险分配的过程中应该与银行、承包商结成“联盟1”，威慑政府部门以此来减少己方需要承担的风险；在“联盟1”内部分配风险时，社会资本投资人应与承包商结成“联盟2”，对抗银行以此来减少己方的风险比例。二是建议社会资本充分准备谈判信息。主要是尽可能了解对方的信息与策略，减少信息不对称情况，从而有效减少己方所承担的PPP项目风险比例。