剖析立体几何中的经典题型

■河南省沈丘县第一高级中学 董晓霞

立体几何中的证明线面平行、线线垂直、线面垂直,以及几何体的外接球问题是经典题型,也是高考的热点,本文总结了一些方法思路,希望对同学们的学习能有所帮助。

一、证明线面平行

证明方法：(1)利用线面平行的判定定理证线面平行：a⊄α,b⊂α,a∥b⇒a∥α。

(2)利用面面平行的性质定理证线面平行：α∥β,a⊂α⇒a∥β。

(3)利用空间向量进行证明。

例1 如图1,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点。求证：GF∥平面ADE。

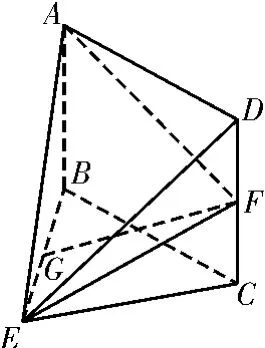
图1

证法一：如图2,取AE的中点H,连接HG,HD。又G是BE的中点,所以GH∥AB,且。因为F是CD的中点,所以。由四边形ABCD是矩形得AB∥CD,AB=CD,所以GH∥DF,且GH=DF。从而四边形HGFD是平行四边形,所以GF∥DH。又DH⊂平面ADE,GF⊄平面ADE,所以GF∥平面ADE。

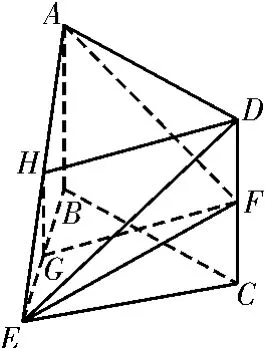
图2

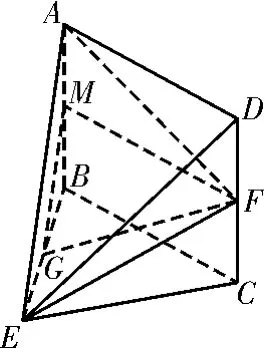
图3

证法二：如图3,取AB的中点M,连接MG,MF。又G是BE的中点,可知GM∥AE。又AE⊂平面ADE,GM⊄平面ADE,所以GM∥平面ADE。在矩形ABCD中,由M、F分别是AB、CD的中点,得MF∥AD。又因为AD⊂平面ADE,MF⊄平面ADE,所以MF∥平面ADE。又因为GM∩MF=M,GM⊂平面GMF,MF⊂平面GMF,所以平面GMF∥平面ADE。因为GF⊂平面GMF,所以GF∥平面ADE。

点评：直线和平面平行首先是利用其判定定理,或者利用面面平行的性质来证,注意线线平行、线面平行、面面平行的转化;有中点时寻找中位线,利用三角形的中位线平行于底边、平行四边形的对边平行等有关性质。

例2 如图4,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,M和N分别为B1C和D1D的中点。求证：MN∥平面ABCD。

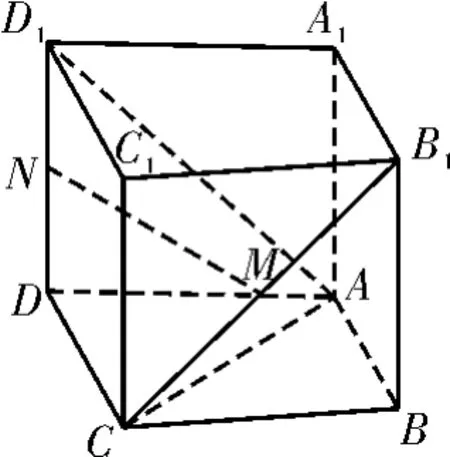
图4

解析：如图5,以A为原点建立空间直角坐标系,依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,-2,0)。

因为M,N分别为B1C和D1D的中点,所以1)。

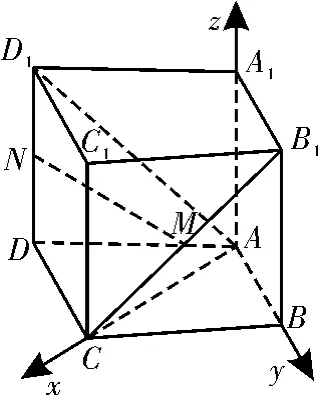
图5

依题意可得n=(0,0,1)为平面的一个法向量,因为,所以又因为直线MN⊄平面ABCD,所以MN∥平面ABCD。

点评：当直线的方向向量与平面的法向量垂直时,直线和平面平行,但要注意指出直线不在平面内。

二、证线线垂直、线面垂直

证明方法：(1)证线线垂直：①用勾股定理;②转化为证线面垂直。

(2)证线面垂直：①用线面垂直的判定定理：a⊂α,b⊂α,a∩b=P,l⊥a,l⊥b⇒l⊥α;②用面面垂直的性质定理：α⊥β,α∩β=b,a⊂α,a⊥b⇒a⊥β。

(3)证面面垂直：①用面面垂直的判定定理：l⊥α,l⊂β⇒α⊥β;②用定义法,证两平面所成二面角的平面角为直角。证明时注意线线垂直、线面垂直、面面垂直的转化。

例3 如图6,在四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD= ∠CBD,AB=BD。证明：平面ACD⊥平面ABC。

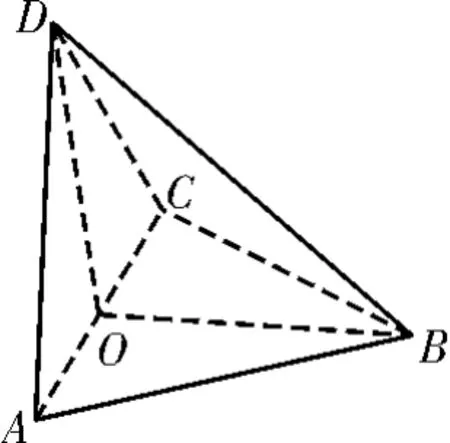
图6

解析：由题设可得△ABD≌△CBD,从而AD=DC。因为△ACD是直角三角形,所以∠ADC=90°,取AC的中点O,连接BO,DO,则DO⊥AC,DO=OC。因为△ABC是正三角形,所以BO⊥AC,所以∠DOB为二面角D-AC-B的平面角。在△AOB中,BO2+AO2=AB2,又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2。所以∠DOB=90°,所以平面ACD⊥平面ABC。

点评：本题证线线垂直时利用勾股定理,证面面垂直时通过证两平面的二面角为直二面角,利用了定义法证明。

三、求空间角

空间角主要有：异面直线所成的角、直线与平面所成的角、两平面所成的角。

(1)求异面直线所成的角,一是几何法,通常作平行线找出异面直线所成的角,在三角形中解出该角,注意异面直线所成的角的取值范围是,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角;二是坐标法,需求出它们的方向向量a,b的夹角,则

(2)求直线与平面所成的角,一是寻求过直线上一点作平面的垂线,再作出直线与平面所成的角;二是转化为直线的方向向量和平面的法向量的夹角,可先求出平面α的法向量n与直线l的方向向量a的夹角,则sinθ=|cos〈n,a〉|。

(3)求二面角α-l-β的大小θ,一是转化为两平面法向量的夹角,先求出两平面的法向量n1,n2所成的角,则θ=〈n1,n2〉或π-〈n1,n2〉;二是用几何法,作出二面角的平面角,在三角形中求平面角的大小。

(4)利用法向量求解空间角在于四个关键步骤：

第一步,建立适当的空间直角坐标系;

第二步,准确求解相关点的坐标;

第三步,求出平面的法向量;

第四步,求夹角。

例4 如图7,在三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是____。

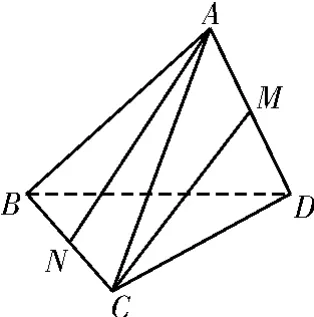
图7

解析：如图8,连接DN,取DN的中点P,连接PM,PC,则可知∠PMC(或其补角)即为异面直线AN,CM所成的角。易得所以即异面直线AN与CM所成的角的余弦值为

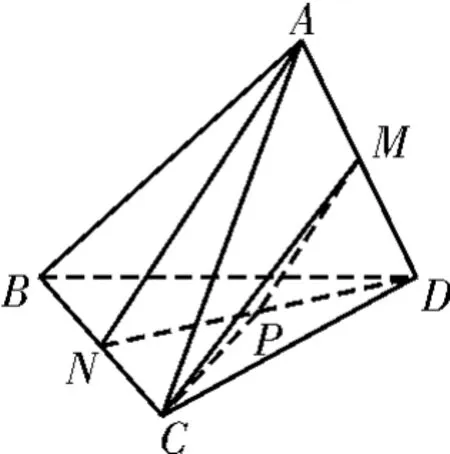
图8

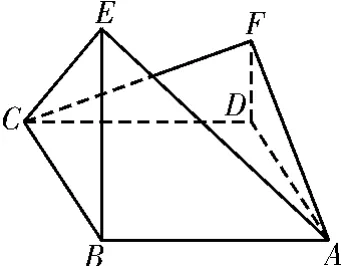
图9

例5 如图9,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC。

(1)证明：平面AEC⊥平面AFC;

(2)求直线AE与直线CF所成角的余弦值。

解析：(1)连接BD,设BD∩AC=G,连接EG,FG,EF,如图10所示。

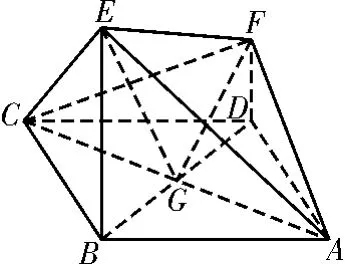
图10

在菱形ABCD中,不妨设GB=1,由∠ABC=120°,可得。由BE⊥平面ABCD,AB=BC,可知AE=EC。又因为AE⊥EC,所以

在 R t△EBG中,可得,故在R t△FDG中,可得

在直角梯形BDFE中,由,可得,所以,所以EG⊥FG。

因为AC∩FG=G,所以EG⊥平面AFC。因为EG⊂面AEC,所以平面AFC⊥平面AEC。

(2)如图11,以G为坐标原点,分别以的方向为x轴,y轴正方向为单位长度,建立空间直角坐标系G-x y z。由(1)可得所以

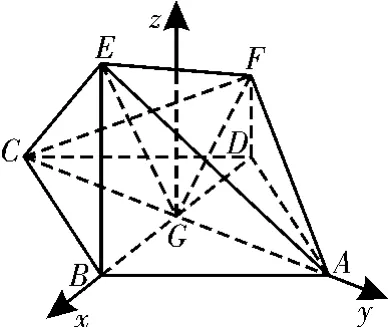
图11

例6 如图12所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,E为棱PC的中点。

(1)证明：BE⊥DC;

(2)求直线BE与平面PBD所成角的正弦值;

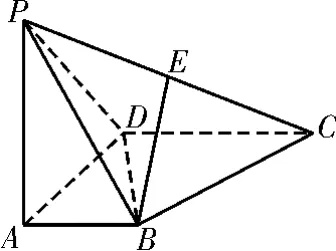
图12

(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值。

解法一：依题意,以点A为原点建立空间直角坐标系(如图13所示),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2)。由E为棱PC的中点,得E(1,1,1)。

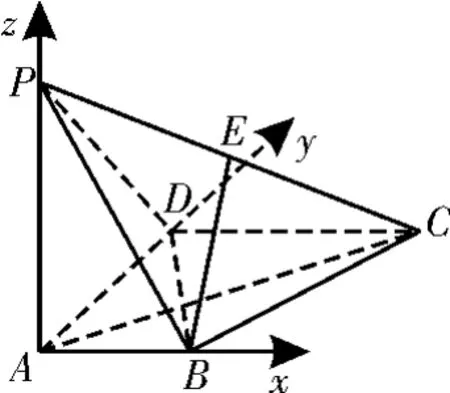
图13

不妨令y=1,可得n=(2,1,1)为平面PBD的一个法向量。于是有,所以直线BE与平面PBD所成角的正弦值为

设n1=(x,y,z)为平面FAB的法向量,则

不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量。

取平面ABP的法向量n2=(0,1,0),则

易知二面角F-AB-P是锐角,所以其余弦值为

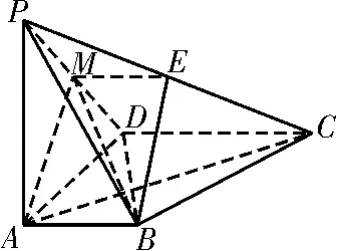
图14

解法二：(1)如图14所示,取PD中点M,连接EM,AM。由于E,M分别为PC,PD的中点,故EM∥DC,且EM=。由已知可得EM∥AB且EM=AB,故四边形ABEM为平行四边形,所以BE∥AM。因为PA⊥底面ABCD,故PA⊥CD,而CD⊥DA,从而CD⊥平面PAD。因为AM⊂平面PAD,所以CD⊥AM。又BE∥AM,所以BE⊥CD。

(2)连接BM,由(1)得CD⊥平面PAD,得CD⊥PD。而EM∥CD,故PD⊥EM。又因为AD=AP,M为PD的中点,所以PD⊥AM,可得PD⊥BE,所以PD⊥平面BEM,故平面BEM⊥平面PBD,所以直线BE在平面PBD内的射影为直线BM。而BE⊥EM,可得∠EBM为锐角,故∠EBM为直线BE与平面PBD所成的角。依题意有,而M为PD的中点,可得,进而。故在R t△BEM中,,因此,所以直线BE与平面PBD所成角的正弦值为

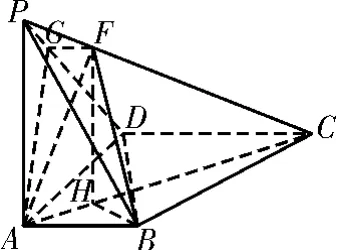
图15

(3)如图15所示,在△PAC中,过点F作FH∥PA交AC于点H。因为PA⊥底面ABCD,所以FH⊥底面ABCD,从而FH⊥AC。又BF⊥AC,得AC⊥平面FHB,因此AC⊥BH。在底面ABCD内,可得CH=3HA,从而CF=3FP。在平面PDC内,作FG∥DC交PD于点G,于是DG=3GP。由于DC∥AB,故GF∥AB,所以A,B,F,G四点共面。由AB⊥PA,AB⊥AD,得AB⊥平面PAD,故AB⊥AG,所以∠PAG为二面角F-AB-P的平面角。在△PAG中,PA=2,PG=再由余弦定理可得,所以二面角F-AB-P的余弦值为

点评：解决线线垂直、线面垂直及求二面角问题,要熟练利用有关垂直的判定定理和性质定理进行面面垂直、线面垂直、线线垂直之间的转化与证明,另外利用空间向量解题时,要建立适当的直角坐标系,准确写出空间点的坐标,利用法向量求二面角,利用数量积为零,解决线线、线面垂直问题。

跟踪练习：

1.如图16,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,O为EF的中点。求证：AO⊥BE。

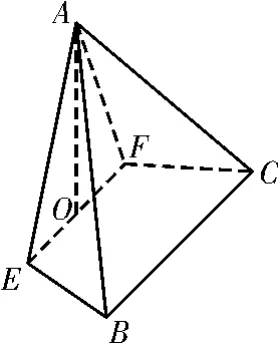
图16

证明：△AEF为等边三角形,O为EF的中点,所以AO⊥EF。因为平面AEF⊥平面EFCB,平面AEF∩平面EFCB=EF,AO⊂平面AEF,所以AO⊥平面EFCB。因为BE⊂平面EFCB,所以AO⊥BE。

2.如图17,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°。

(1)证明：平面PAB⊥平面PAD;

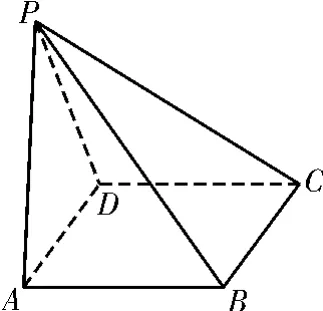
图17

(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值。

解析：(1)由已知∠BAP=∠CDP=90°,得BA⊥PA,CD⊥PD。由于AB∥CD,故AB⊥PD,从而AB⊥平面PAD。又AB⊂平面PAB,所以平面PAB⊥平面PAD。

(2)在平面PAD内作PF⊥AD,垂足为F,由(1)可知,AB⊥平面PAD,故AB⊥PF,可得PF⊥平面ABCD。

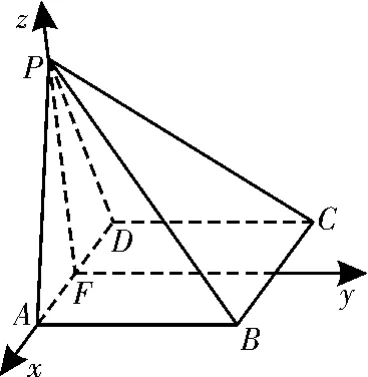
图18

以F为坐标原点,的方向为x轴正方向为单位长,建立如图18所示的空间直角坐标系F-x y z。

设n=(x,y,z)是平面PCB的法向量,则可取

设m=(x,y,z)是平面PAB的法向量,则可取m=(1,0,1)。

3.如图19,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,

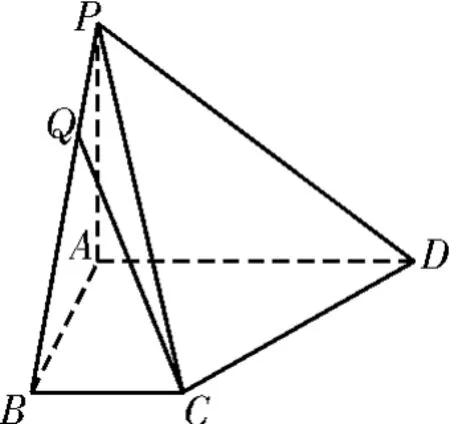
图19

(1)求平面PAB与平面PCD所成二面角的余弦值;

(2)点Q是线段BP上的动点,当直线CQ与DP所成角最小时,求线段BQ的长。

解析：以A为坐标原点,建立如图20所示的空间直角坐标系A-x y z,则Β(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2)。

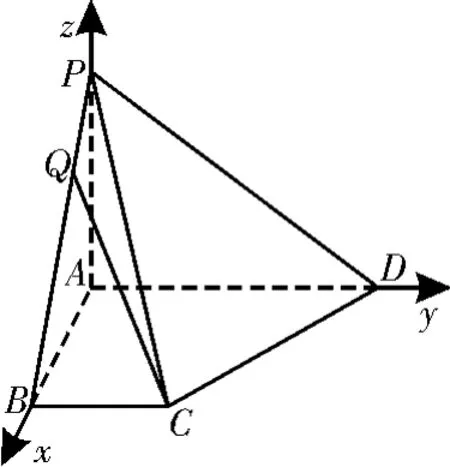
图20

(1)因为Α D⊥平面Ρ Α Β,所以是平面Ρ Α Β的一个法向量