作业的分层源于课堂教学的分层——由一道数学题引发的分层思考
江苏科技大学附属中学 丁 震
【摘 要】 通过课堂分层教学、布置分层作业,让每位学生都学有价值的数学,每个人都能获得必需的数学,不同的人在数学上得到不同的发展,是课标的总体要求之一。文章由一道数学题入手,从课堂分层教学出发了解了学生的学情,找到了分层的“点”,进而布置分层作业,为教师分层教学提供了有效的教学策略。
【关键词】 数学;作业;分层教学
在数学教学中,很多老师对课堂分层教学及分层作业表示认同,但又感觉难以操作,认同是都知道教学应该“因材施教”,难以操作是感觉不同层次的学生放在一起,教不同层次的内容难免会顾此失彼,最后分层也就不了了之。我觉得最大的问题在于这是对“分层”的理解不够,对课堂分层教学与分层作业的关系没有理清。
下面我就一道七年级的数学题谈谈我对分层的思考。
题目:已知a-2b=2,则4+2a-4b 的值是______________。
很多老师在处理这类题目时,总是直接让学生观察已知条件中含字母的项与所求式子中含字母的项之间有何联系,效果很不好。为什么?因为七年级的孩子的认知水平还停留在小学“数”的层面上,数是一个定值,字母可以取不同的数,是变化的,而含字母的代数式又会随着字母的变化而变化,所以大部分学生听得是一团雾水,作业中遇到同类型的题目无从入手,而老师却觉得学生太笨,感到无所适从。
怎么办?关键在引导,如何引导?关键在分层。
我在课堂教学中做了如下尝试。
解题思路:引导学生关注已知条件中含字母的项与所求式子中含字母的项之间有何联系。
一、基础层次
(分层的起点)
由具体到抽象,取特殊值列表观察。
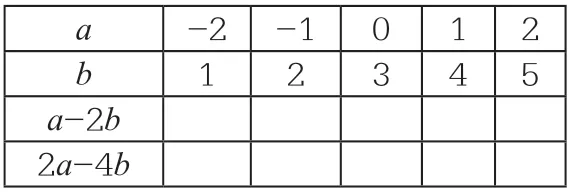
?
问:字母a、b 变化了,式子a-2b 与2a-4b 的值是否也在改变?它们的数量关系如何?
再任取a、b 的值试一试。
学生会发现:无论a、b 的值如何改变,2a-4b 的值总是a-2b的值的两倍。
作为一名数学教师,平时应加强对典型题目的研究和对学情的了解,其中研究契合学生学习的“切入点”尤为重要,因为这个“切入点”是教学的“起点”,往往就是分层的“起点”,起点低了,学生不愿学;起点高了,学生又不会学。很多教师分层教学不成功的源头往往就是没能抓好这个“起点”。这里我的处理是从学生熟悉的具体的“数”入手,而非“直接观察”,遵循教学的起点应该从学生的“最近发展区”切入,“引导”学生慢慢进入主题“观察字母”——“观察代数式”,学生易于接受。
二、能力提升
师:你能利用所学知识说一说理由吗?
(问题的分层)
甲:把结论用式子表达就是2a-4b=2(a-2b),这就是乘法分配律的逆运算。
乙:我发现2a 是a 的2 倍,-4b 是-2b 的2 倍,所以2a-4b 的值总是a-2b 的值的两倍。
师:那大家能说一说解这类题目的方法吗?
(方法的分层)
丙(基础层次):我用特殊值代入的方法,通过计算来找两个式子中含字母的项的联系。
丁(中等水平层次):我选乙同学的方法,直接观察两个式子中含字母的项的联系。
这一教学环节是本题的重点,教师的第一个设问“你能利用所学知识说一说理由吗”虽然是一个问题,但不同层次的学生有不同的理解,也就有不一样的理由,所以这其实就是问题的分层。教师的第二个设问“那大家能说一说解这类题目的方法吗?”其实一方面是引导学生归纳解法,另一方面也是让不同的学生选择适合自己的方法,这就是方法的分层。
三、能力拓展
回到题目:已知a-2b=2,则4+2a-4b 的值是___________ 。
师:你还有什么方法解决上面的问题?
(方法的进一步分层)
同学们陷入沉思。
师:前面的解法关键是找到已知条件中含字母的式子与所求式子中含字母的式子的数量关系,整体代入,从而消去了字母的解,那么我们可以利用已知条件,用一个字母的式子去表示另一个字母,再代入求解吗?
同学们开始热烈讨论。
师:太棒了,大家试一试!你上黑板来板书。
很快大家就得到答案。
师又问:除了用含b的式子表示a,能不能用含a的式子表示b呢?
同学们尝试之后一致认可。
师:哪种方法简单?为什么?
大家讨论后发现a 的系数较简单,所以用含b 的式子表示a 更好。
师:通过以上的学习,这类题目可以有三种方法,最后一种方法更具有一般性,是代入法的通法。
分层作业:
1.基础题:(要求根据你的理解写出解题过程,鼓励一题多解)已知代数式x+2y=3,则代数式2x+4y-5 值是______________。
2.能力题:(选做)
当x=2016 时,整式px3+qx+1 的值等于2,那么当x=-2016 时,整式px3+qx+1 的值为多少?
3.拓展题:(选做)
①当x=0 时,求a0的值;
②求a1+a2+a3+a4+a5的值。
正是有了课堂教学的分层,我设计了上面的分层作业,因为我通过课堂分层教学进一步了解了学生对这类题目的掌握情况,找到了分层的“点”,所以我分了三个层次的问题,学生也可以各取所需。
通过这道七年级的数学题教学,我认为作业的分层源于课堂教学的分层,课堂分层教学不仅仅是不同题目的分层,也可以是同一个题目的不同层次问题的分层、不同解法的分层。同一个题目的不同层次问题的分层蕴含着数学的重要思想方法——从具体到抽象,从特殊到一般,层层递进,同时也符合学生学习的认知规律;而不同解法的分层不仅有利于培养学生的发散思维,而且也让不同水平层次的学生各有收获。正是有了课堂教学的分层,才能让教师为学生提供作业更精准,学生在完成作业时能根据自己的理解选择适合自己的题目和适合自己的方法,从而达到真正意义上的分层。

