双时滞HollingⅡ型的四维捕食模型的Hopf分支

李志宏， 柴玉珍

(太原理工大学 数学学院， 山西 太原 030024)

0 引 言

时滞微分方程组在许多工业工程和自然科学领域具有重要的应用背景， 有关对时滞微分方程组的研究在近几年也取得了丰硕的成果.Yan X P等[1-2]研究了具有单时滞和双时滞的二维捕食模型正平衡点的稳定性和Hopf分支. Collera J A[3-4]等研究了双时滞的3种群捕食模型的Hopf分支. 随后考虑到影响种群持久与灭绝的重要因素， 许多学者又研究了带有功能性反应函数的捕食模型， Zhu H等[5]研究了双时滞HollingⅡ型的3种群食物链系统的Hopf分支. Li L C等[6]在考虑单时滞HollingⅡ型的两种群模型在平衡点处的稳定性及Hopf分支存在性的基础上， 使用无穷维系统的持久性理论证明了模型的持久性. Wen J J等[7-9]研究了具有单时滞的HollingⅣ型的3种群捕食模型和具有双时滞HollingⅡ型的3种群捕食模型的Hopf分支， 利用规范型理论和中心流行定理得出确定该系统Hopf分支方向和分支周期解稳定性的计算公式. 丁建华等[10]针对具有HollingⅣ型的二维捕食模型讨论了系统的有界性、 正平衡点处的稳定性， 并通过构建Lyapunov函数证明了正平衡点处的全局渐近稳定性. 鉴于前人的研究， 本文综合时滞和Holling型函数这两个因素， 研究如下四维捕食模型

(1)

式中：x1(t),x2(t),x3(t),x4(t)分别为一级、 二级、 三级食饵和捕食者这4个种群在t时刻的种群密度； 参数r1,r2,r3,r4分别为一级食饵的内禀增长率， 二级、 三级食饵的死亡率和捕食者的自然死亡率；a1为自身的竞争率；a2,a3,a5,a8分别为其捕获率；a4,a6,a7,a9分别为其消化率， 且都为正常数；m为半饱和度；τ1为追捕时间；τ2为成熟期. 下假设x2,x3,x4三种群有相同的追捕时间和成熟期， 且τ=τ1+τ2. 基于种群密度的实际意义， 系统(1)定义在

x2≥0,x3≥0,x4≥0}

1 正平衡点的存在性

鉴于系统(1)的生物意义， 只考虑其正平衡点.

定理1 若满足条件

H1)a>0，

H2)b>0，

或H3)a<0，d>0，d2+4a9a2a4ma>0，

其中

a=-r2a1a9+a4r1a9-a3r4a4-a5r4a1,

2a9a2a4(c+a7a5r4m),

2a9a2a4(c+a7a5r4m),

c=-r3a4a9m+a7r2a9m,

d=am-a9a2a4，

证明若系统(1)存在正平衡点， 则应有

成立， 从而可解的系统(1)满足条件H1),H2)有正平衡点E*； 满足条件H3),H4)有正平衡点E**.

2 正平衡点的稳定性及Hopf分支的存在性

下面考虑正平衡点E*，E**可类似讨论.

系统(1)在正平衡点E*处的Jacobian矩阵为

进而可以求得系统(1)在正平衡点E*处的特征方程为

λ4+p1λ3+p2λ2+p3λ2e-λτ1e-λτ2+p4λ+p5λe-λτ1e-λτ2+

p6λe-λτ2+p7λe-λτ1+p8e-λτ1e-λτ2=0,

(2)

下面根据时滞τ1,τ2分3种情形讨论.

情形1τ1=τ2=0.

当τ1=τ2=0时， 式(2)可化为

λ4+p1λ3+(p2+p3)λ2+

(p4+p5+p6+p7)λ+p8=0.

(3)

由Hurwitz判据[11]可知， 式(3)的根具有负实部需满足条件H5),H6),H7),H8). 其中：

此时有下面的结论.

定理2τ1=τ2=0， 且满足条件H5),H6),H7),H8)时， 系统(1)在正平衡点E*是渐近稳定的.

情形2τ1>0,τ2=0.

当τ1>0,τ2=0， 式(2)可化为

λ4+p1λ3+p2λ2+(p4+p6)λ+

(p3λ2+p5λ+p7λ+p8) e-λτ1=0.

(4)

令λ=iω是式(4)的一个纯虚根， 代入式(4)并分离实部和虚部， 则有

(5)

消去cosωτ1和sinωτ1可得

(6)

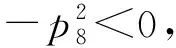
记式(6)的8个根为ωi(i=1,2,…,8)， 分别将其代入有

从而有

由Butler[12]引理可得， 系统(1)的正平衡点E*在τ1<τa时是渐近稳定的. 式(2)对τ1求导有

所以

式中：

综上分析， 若满足

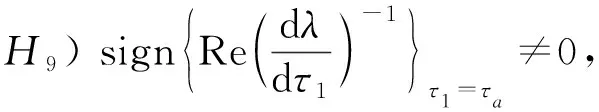
情形3τ1>0，τ2>0.

取τ1∈(0,τa)， 下面讨论时滞τ2.

令λ=iω是式(2)的一个纯虚根， 代入式(2)并分离实部和虚部， 则有

(7)

化简上式得

(8)

式中：

g4=2p7ω5-2p2p7ω3-2p6(p3ω2-p8)ω,

g5=-2p1p7ω4+2(p4p7-p5p6)ω2.

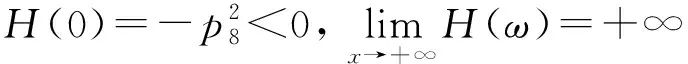
cosωiτi=

从而有

i=1,2,…,k=0,1,2,….

由Butler[12]引理可得， 系统(1)的正平衡点E*在τ2<τb时是渐近稳定的. 在式(2)对τ2求导有

所以

式中：

(2p3ωbsinωbτ1+p5cosωbτ1+p6)cosωbτb,

(2p3ωbsinωbτb+p7)sinωbτ1-(p5cosωbτ1+p6)sinωbτb,

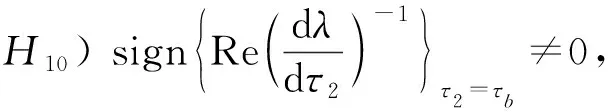
3 举例论证

例在式(1)中取a1=a3=a5=0.4,a2=a6=0.1,a4=r2=r3=r4=m=0.2,a7=a8=0.05,a9=0.3,r1=1.6， 则满足条件H1),H2)， 且正平衡点为E*(1.55,7.14,0.67,3.43). 经验证H5=0.555 1,H6=0.108 5,H7=0.001 3,H8=0.000 06， 所以当τ1=τ2=0时，E*是渐近稳定的(见图 1).

当τ1>0,τ2=0， 计算可取得τa=2.16，τ1∈[0,τa)时E*是渐近稳定的(见图 2).

当τ1>τa时，E*不稳定，τ1=τa时，E*在τa附近产生分支(见图 3).

当τ1>0，τ2>0， 取τ1=1.88∈[0,τa)， 计算可得ωb=0.186，τb=0.215，E*在τ2∈(0,τb)时是渐近稳定的(见图 4).

当τ2>τb时，E*不稳定，τ2=τb时，E*在τb附近产生分支(见图 5).

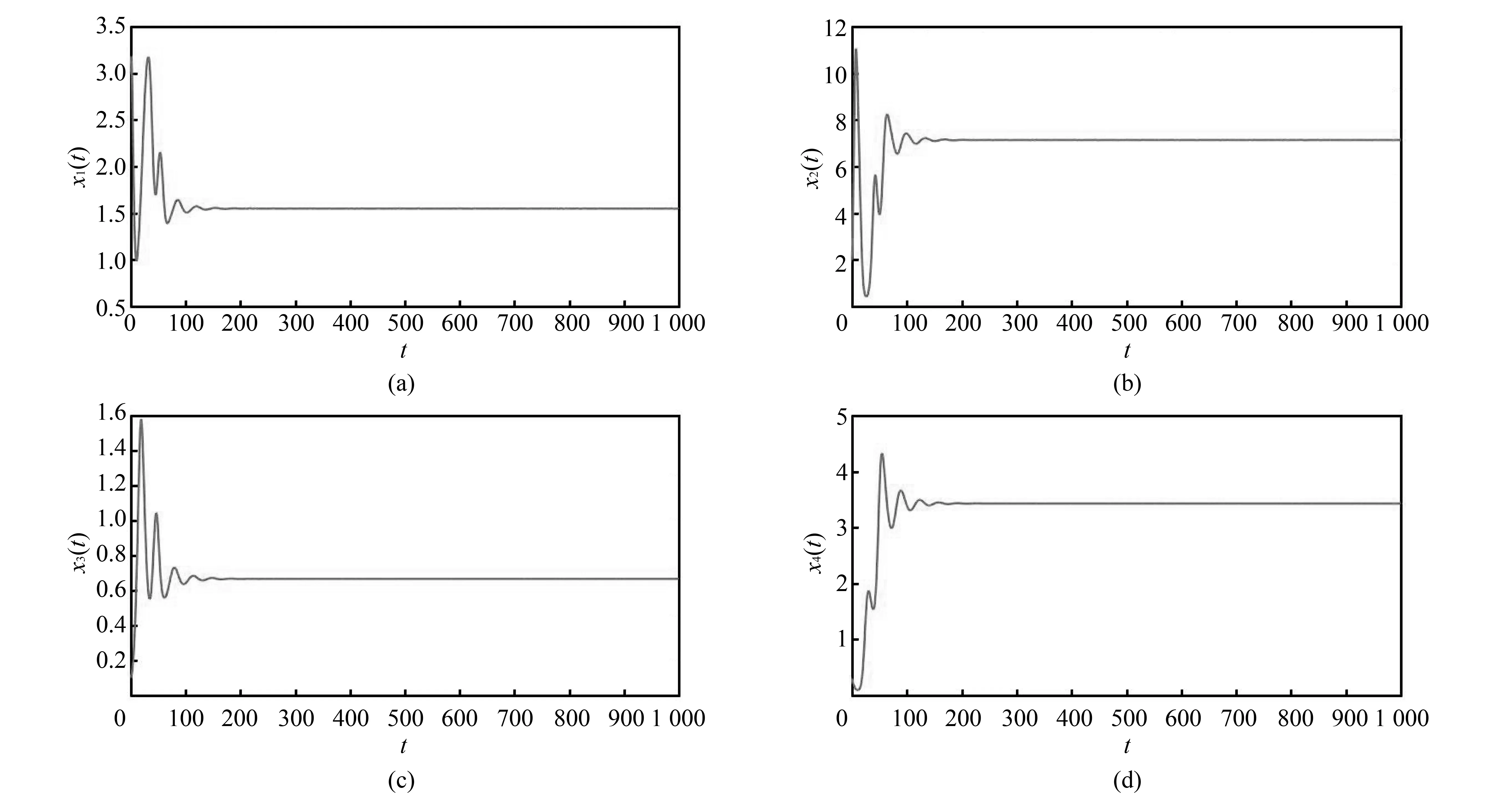
图 1 τ1=τ2=0, 正平衡点E*渐近稳定时分量变化图Fig.1 The behavior of components with asymptotical stability of positive equilibrium point E* as τ1=τ2=0

图 2 τ1=1.78<τa=2.16, τ2=0， 正平衡点E*渐近稳定时分量变化图Fig.2 The behavior of components with asymptotical stability of positive equilibrium point E* as τ1=1.78<τa=2.16, τ2=0

图 3 τ1=3.16>τa=2.16, τ2=0， 正平衡点E*不稳定时分量变化图Fig.3 The behavior of components with instability of positive equilibrium point E* as τ1=3.16>τa=2.16, τ2=0

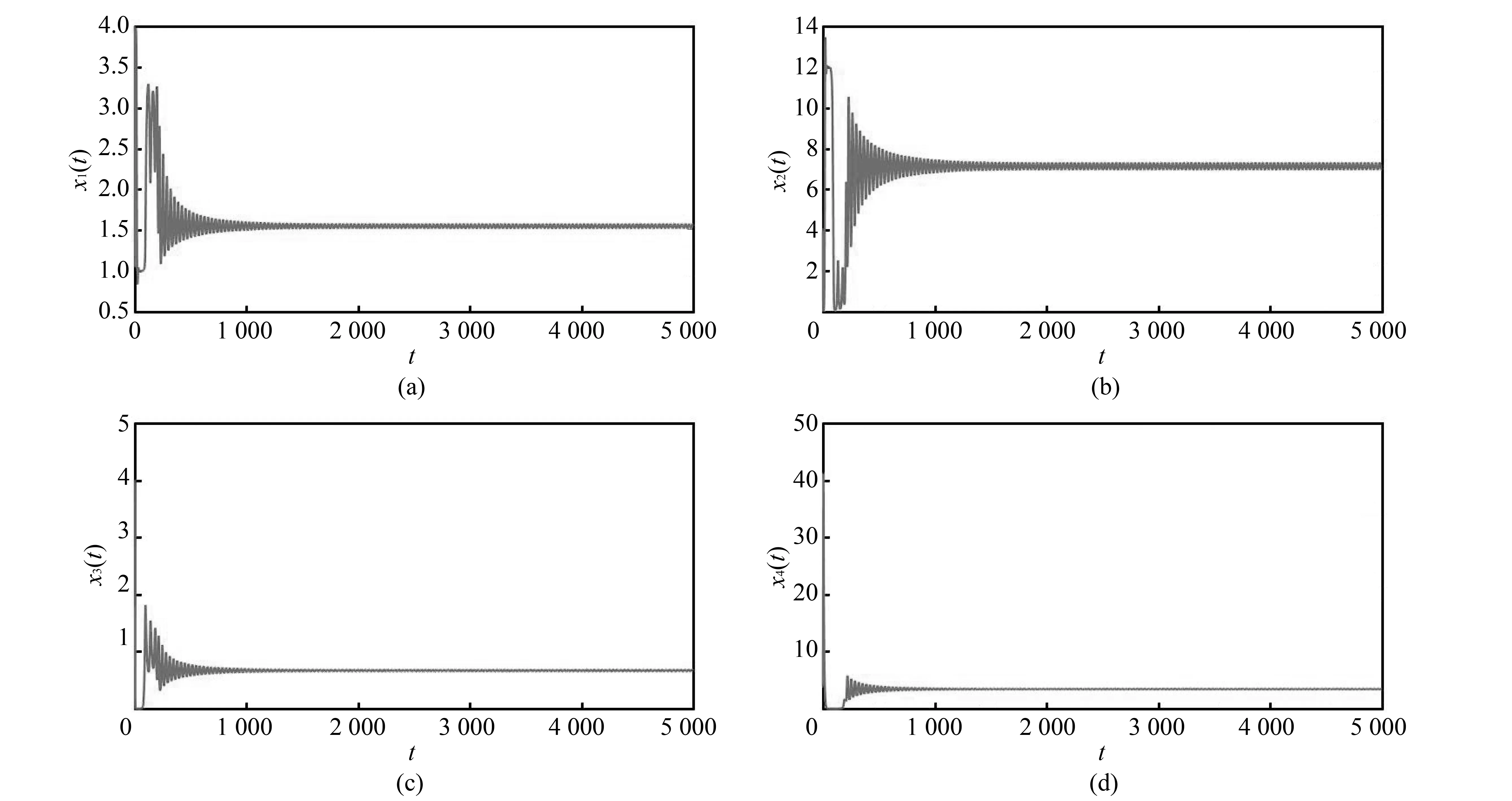
图 4 τ1=1.88, τ2=0.01<τb=0.215， 正平衡点E*渐近稳定时分量变化图Fig.4 The behavior of components with asymptotical stability of positive equilibrium point E* as τ1=1.88, τ2=0.01<τb=0.215

图 5 τ1=1.88, τ2=0.5>τb=0.215， 正平衡点E*不稳定时分量变化图Fig.5 The behavior of components with instability of positive equilibrium point E* as τ1=1.88, τ2=0.5>τb=0.215