钻井用浮箍结构冲蚀安全优化数值模拟研究
陈新海,豆惠萍,王乐顶,李立昌,李 毅,王 锐,杨 恺
(1.渤海钻探工程技术研究院,天津 300457;2.中国石油华北油田勘探开发研究院,河北 沧州 062552;3.渤海钻探井下技术服务分公司,天津 300283)
套管用浮箍、浮鞋是重要的固井附件之一,主要作用是防止水泥浆倒返,保证固井质量。固井作业时,通常至少要循环两个循环周以上,遇到井下复杂情况、工序衔接出现问题时,有时需要等待24 h以上。尽管可以通过降低排量、间断循环等方式规避井下风险,但因固井过程中浮箍、浮鞋等附件失效,造成影响固井质量的事故仍时有发生[1-3]。这类问题在重点井、储气库井中尤为突出,一方面是重点井现场决断机制不健全所致,另一方面也凸显出对套管用浮箍、浮鞋抗冲蚀能力的质疑。
为了重新认识套管用浮箍、浮鞋在钻井液循环过程中的冲蚀失效机理,本文对现场普遍使用的弹簧式浮箍和舌板式浮箍流场展开了有限元数值模拟研究。通过在大型ANSYS仿真软件中建立浮箍流场CFD模型,结合对钻井液性能中含砂粒径和含砂浓度的控制,定量模拟研究不同阀芯开度下含有固相颗粒的多相流对浮箍阀体的冲蚀速率,并建立冲蚀速率与固相颗粒含量、固相颗粒大小、阀芯开启度的关系曲线,总结其冲蚀机理,以为浮箍的结构优化提供理论依据,为现场作业提供指导,为进一步研发新产品夯实理论基础。
1 CFD建模
1. 1 紊流控制方程
在固井注水泥前的循环中,浮箍相对于套管串截面流道尺寸小,流场狭窄,既定排量下流速高,即此流动为两相紊流流动,连续相泥浆采用RNG的k-ε方程描述,其方程如下[4-8]:
(1)
(2)
式中:t为时间(s);ρ为泥浆密度(kg/m3);k为湍动能(m2/s2);x为位移(m);u为速度(m/s);Gk为由层流速度梯度产生的湍流动能[N/(m2·s)];ueff为有效黏度(Pa·s);Gb为由浮力产生的湍流动能[N/(m2·s)];αk为k方程Prandt1数(无因次);C1ε、C2ε、C3ε为经验参数(无因次);ε为单位质量的湍动能耗散率(m2/s3);αε为ε方程Prandt1数(无因次);Sk、Sε为自定义参数[N/(m2·s)];Rε为ε的函数(无因次);下标i、j、k表示x、y、z方向。
1.2 Finnie体积冲蚀磨损理论
在钻井液循环过程中,流体中的固相颗粒在高速率下连续不断地冲击浮箍浮鞋阀芯、阀体,发生能量转换,在冲击面上发生体积冲蚀,阀芯或阀体产生局部微破碎,剥离后造成浮箍浮鞋等固井附件的失效,影响固井质量。
在浮箍的冲蚀磨损机理研究中,固体颗粒(即砂粒)在浮箍密封面上的冲蚀,可通过下式计算得到N个岩屑颗粒在钻井液的携带下冲蚀浮箍的冲蚀速率[4-8]:
(3)
式中:ER为冲蚀速率[kg/(m2·s)];mpn为砂粒质量流量(kg/s);dpn为砂粒直径(mm);C(dpn)为砂粒直径函数;f(α)为冲蚀攻角的函数;N为砂粒数(无因次);vpn为砂粒相对速度(m/s);b(vpn)为砂粒相对速度函数(m/s);Af为浮箍密封面单位冲蚀面积(m2)。
由砂粒对浮箍的相对速度及冲蚀规律,可得到公式(3)中几个函数的表达式如下:
砂粒相对速度函数为
b(vpn)=1.73
(4)
砂粒直径函数为
C(dpn)=1 559B-0.59fs×10-7
(5)
对于弹簧式浮箍橡胶阀芯(见图1),冲蚀攻角的函数为
f(α)=0+7.592 4α+6.126 9α2-11.928α3+3.813 4α4
(6)
对于舌板式浮箍铝(见图2),冲蚀攻角的函数为
(7)
上式中:B为布氏硬度(N/mm2),材料表面强度越坚硬,B值越大;fs为砂粒的形状系数(无因次),fs越大,对浮箍的冲蚀力越大(其中,fs=0.20表示砂粒为球形;fs=0.53表示砂粒为半圆形;fs=1.00表示砂粒外形锋利),fs一般取值在0.50~0.70范围内,经验值fs=0.60比较符合浮箍冲蚀机理研究的实际情况;α为砂粒的冲蚀攻角(rad)。

图1 弹簧式浮箍橡胶阀芯冲蚀攻角与冲蚀攻角函数曲线[9]Fig.1 Curve of erosion attack angle of rubber valve core of the spring floating hoop[9]

图2 舌板式浮箍铝冲蚀攻角与冲蚀攻角函数曲线[10]Fig.2 Curve of erosion attack angle of the tongue floating hoop[10]
1. 3 固相颗粒受力模型
固相颗粒在浮箍流场内的运动中主要受到重力、浮力、压力梯度力、萨夫曼升力、附加质量力以及内壁的反力等的作用,其受力复杂,力学模型如下[4-5]:
重力为
W=Vpρpg
(8)
浮力为
FB=Vpρgg
(9)
压力梯度力为
(10)
萨夫曼升力为
(11)
附加质量力为
(12)
上式中:W为砂粒重力(N);Vp为砂粒体积(m3);ρp为砂粒密度(kg/m3) ;g为重力加速度(9.8 m/s2);ρg气体密度(kg/m3);∂p/∂l为压强梯度(N/m);vL为泥浆速度(m/s);vp为砂粒速度(m/s);d为流体速率张量(无因次);ap为砂粒加速度(m/s2);下标m、n、k、l为节点编号。
1. 4 浮箍阀件几何结构模型
本文以现场应用较多的弹簧式和舌板式两种浮箍为例进行分析研究。
如图3和图4所示规格的弹簧式浮箍几何模型结构尺寸为:D=6 cm,H=4 cm,D1=8.5 cm,D2=12.5 cm,h=4.1 cm,h1=h2=4.5 cm,h3=4.4 cm。
弹簧式浮箍的开启度对优选弹簧的弹性系数有决定性作用,为此本文分别对弹簧式浮箍不同开启高度(L=1 cm、2 cm、3 cm、4 cm、5 cm、6 cm、7 cm、8 cm)进行建模。

图3 弹簧式浮箍流道几何模型Fig.3 Geometric model of the flow channel of the spring floating hoop

图4 弹簧式浮箍阀芯蘑菇头Fig.4 Mushroom head of the valve core of the spring floating hoop
如图5、图6和图7所示规格的舌板式浮箍几何模型结构尺寸为:D=5 cm,D1=8 cm,D2=12 cm,T=0.4 cm,H=6 cm,H1=2 cm,H2=10 cm,d=7 cm,d1=7.2 cm。
舌板式浮箍的开启度对优选弹簧的弹性系数有决定性作用,为此本文分别对舌板式浮箍不同开启角度(A=10°、20°、30°、40°、50°、60°、70°、80°)进行建模。

图5 舌板式浮箍流道几何模型Fig.5 Geometric model of flow channel of tongue floating hoop

图6 舌板式浮箍密封橡胶圈Fig.6 Sealing rubber ring of the tongue floating hoop

图7 舌板式浮箍舌板Fig.7 Tongue plate of the tongue floating hoop
1. 5 边界条件
入口为速度入口,以D为216 mm井眼一般循环排量为32 L/s为例,弹簧式浮箍阀芯流场入口速度v为11.32 m/s,舌板式浮箍阀芯流场入口速度v为16.31 m/s;出口为压力出口,设定出口压降P为1 MPa。液体钻井液具有不可压缩性。
2 浮箍冲蚀机理研究
2. 1 冲蚀速率与砂粒直径的关系分析
2.1.1 弹簧式浮箍冲蚀速率与砂粒直径的关系
当弹簧式浮箍开启高度L为40 mm、含砂量为0.1%时,弹簧式浮箍阀芯蘑菇头上冲蚀速率与砂粒直径的关系曲线,见图8。

图8 弹簧式浮箍阀芯蘑菇头上冲蚀速率与砂粒直径的关系曲线Fig.8 Relationship curve of the mushroom head erosion rate of the valve core of the spring floating hoop with the sand size
由图8可见,总体上弹簧式浮箍冲蚀速率随着砂粒直径的增加而增加,但随着砂粒直径的增加,其冲蚀速率增加的幅度变缓,且变化幅度不大。
不同砂粒直径下弹簧式浮箍阀芯蘑菇头上冲蚀速率云图见图9,弹簧式浮箍流场速度矢量图见图10。
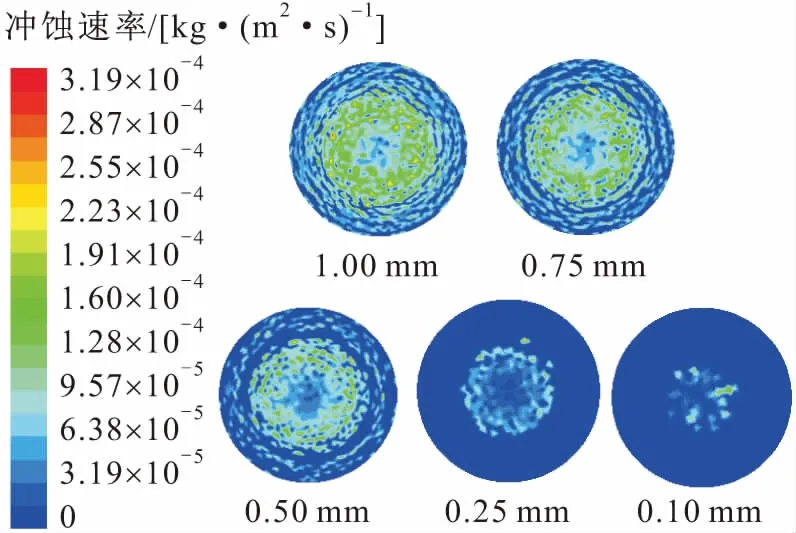
图9 不同砂粒直径下弹簧式浮箍阀芯蘑菇头上冲蚀速率云图Fig.9 Erosion rate cloud of the mushroom head of the valve core of the spring floating hoop under different grand sizes

图10 弹簧式浮箍流场速度矢量图Fig.10 Diagram of the velocity vector of the spring floating hoop flow field
由图9和图10可见,流体首先在弹簧式浮箍阀芯蘑菇头中心位置产生冲击,然后在蘑菇头表面流场发生改变(见图10);蘑菇头中心附近冲蚀最为严重,蘑菇头边缘冲蚀最小,且砂粒直径越大边缘附近冲蚀越大(见图9)。其主要原因是由于砂粒直径越大,惯性越大,受流场作用力的影响越小,流体方向改变也越慢;当砂粒直径为0.25 mm和0.10 mm时,除蘑菇头最顶部被冲蚀外,其余部分由于流场的作用,砂粒运动方向发生改变后,绕过蘑菇头流出浮箍;当砂粒直径相对较大时,砂粒运动方向改变慢,不容易绕过蘑菇头流出浮箍,从而在浮箍边缘区域产生冲蚀。
砂粒直径越小对浮箍的冲蚀速率越小,要保证发挥浮箍的功能,首先要强化固控设备使用,严格控制砂粒的直径。蘑菇头边缘附近是弹簧式浮箍阀芯最主要的密封面,流场模拟研究认为该类型浮箍在不利的现场环境中容易先发生阀芯密封件的失效损坏。
2.1.2 舌板式浮箍冲蚀速率与砂粒直径的关系
当舌板式浮箍舌板开启角度为40°、含砂量为0.3%时,浮箍舌板上冲蚀速率与砂粒直径的关系曲线,见图11。

图11 舌板式浮箍舌板上冲蚀速率与砂粒直径的关系曲线Fig.11 Relationship curve of the erosion rate of the tongue floating hoop with the sand size
砂粒在没有流体作用的情况下,砂粒的冲蚀攻角α为50°,由于舌板的阻挡,流体在舌板处的流动方向会发生改变,进而砂粒在流体的作用下其冲蚀攻角会变小;同时又由于砂粒直径的不同,砂粒的直径越大,惯性越大,砂粒在流体的作用下流动方向改变得越小,即砂粒的直径越大,砂粒的冲蚀攻角越大;再由于砂粒冲蚀攻角与冲蚀速率的关系,可以得到总体上砂粒的直径越小,舌板的冲蚀速率越大。
当舌板式浮箍舌板开启角度为40°、含砂量为0.3%时,浮箍密封胶圈冲蚀速率与砂粒直径的关系曲线,见图12。
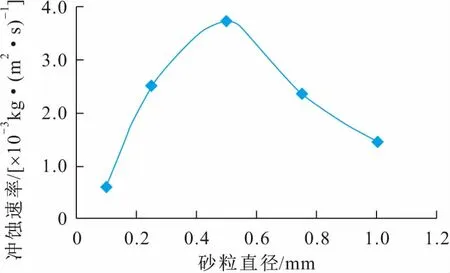
图12 舌板式浮箍密封胶圈冲蚀速率与砂粒直径的关系曲线Fig.12 Relationship curve of the erosion rate of sealing rubber ring of the tongue floating hoop with the grand size
由图12可见,当砂粒在其他条件相同的情况下,0.5 mm的砂粒直径对舌板式浮箍密封胶圈的冲蚀速率最大。
2. 2 冲蚀速率与含砂量的关系分析
2.2.1 弹簧式浮箍冲蚀速率与含砂量的关系
当弹簧式浮箍开启高度L为40 mm、砂粒直径为0.5 mm时,浮箍蘑菇头上冲蚀速率与含砂量的关系曲线,见图13。
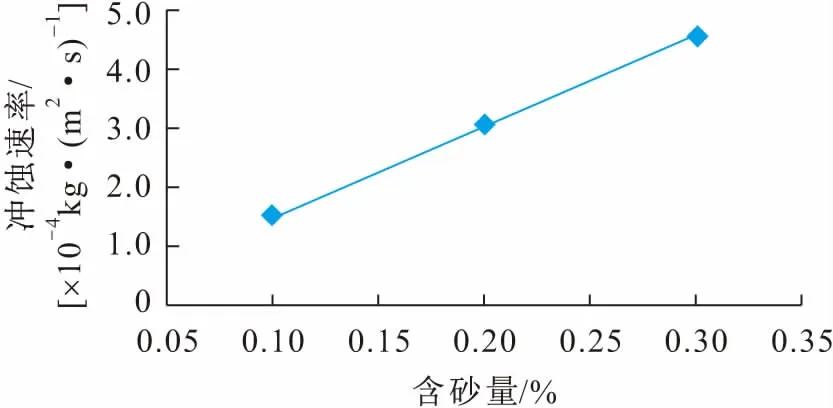
图13 弹簧式浮箍蘑菇头上冲蚀速率与含砂量的关系曲线Fig.13 Relationship curve of the mushroom head erosion rate of the spring floating hoop with the sand concentration
由图13可见,弹簧式浮箍蘑菇头上冲蚀速率随着含砂量的增加呈线性增加。
不同含砂量下弹簧式浮箍蘑菇头上冲蚀速率云图,见图14。

图14 不同含砂量下弹簧式浮箍蘑菇头上冲蚀速率云图Fig.14 Cloud of the mushroom head erosion rate of the spring floating hoop under different sand concentration
由图14可见,含砂量越高,弹簧式浮箍蘑菇头上的冲蚀速率越大。
2.2.2 舌板式浮箍冲蚀速率与含砂量的关系
当舌板式浮箍舌板开启角度为40°、砂粒直径为0.5 mm时,浮箍舌板上和密封橡胶圈上冲蚀速率与含砂量的关系曲线,见图15和16。

图15 舌板式浮箍舌板上冲蚀速率与含砂量的关系曲线Fig.15 Relationship curve of the tongue plate erosion rate of the tongue floating hoop with the grand size

图16 舌板式浮箍密封橡胶圈上冲蚀速率与含砂量的关系曲线Fig.16 Relationship curve of the sealing rubber ring erosion rate of the tongue floating hoop with the sand concentration
由图15和16可见,含砂量越高,舌板式浮箍舌板上和密封胶圈上的冲蚀速率越大。
2. 3 冲蚀速率与浮箍开启度的关系分析
2.3.1 弹簧式浮箍冲蚀速率与浮箍开启高度的关系
弹簧式浮箍阀芯蘑菇头上冲蚀速率与浮箍开启高度L的关系曲线,见图17。

图17 弹簧式浮箍阀芯蘑菇头上冲蚀速率与浮箍开启高度L的关系曲线Fig.17 Relationship curve of the mushroom head erosion rate of the spring floating hoop with the open height L
由图17可见,总体上弹簧式浮箍阀芯蘑菇头上的冲蚀速率随着浮箍开启高度的增加而减小,且在浮箍开启高度较小时,随浮箍开启高度的增加弹簧式浮箍阀芯磨菇头上的冲蚀速率迅速减小,在浮箍开启高度L为40 mm时其冲蚀速率趋于稳定。
不同开启高度度弹簧式浮箍阀芯蘑菇头上冲蚀速率云图,见图18。

图18 不同开启高度下弹簧式浮箍阀芯蘑菇头上冲蚀速率云图Fig.18 Cloud of the mushroom head erosion rate of the spring floating hoop under different opening angle
由图18可见,结合冲蚀速率与浮箍开启高度L的关系曲线,进一步印证了在浮箍开启高度L大于40 mm时,弹簧式浮箍阀芯蘑菇头上的冲蚀速率明显降低。
2.3.2 舌板式浮箍冲蚀速率与浮箍开启角度的关系
舌板式浮箍舌板上冲蚀速率与浮箍开启角度的关系曲线,见图19。
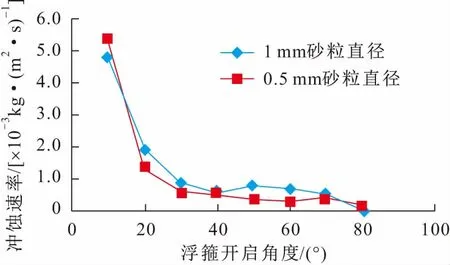
图19 舌板式浮箍舌板上冲蚀速率与浮箍开启角度的关系曲线Fig.19 Relationship curve of the tongue plate erosion rate of the tongue floating hoop with the opening angle
由图19可见,总体上舌板式浮箍舌板上的冲蚀速率随浮箍开启角度的增加而减小,且在浮箍开启角度较小时,随着浮箍开启角度的增加舌板上的冲蚀速率迅速减小,在浮箍开启角度L为30°时其冲蚀速率趋于稳定。
舌板式浮箍密封橡胶圈上冲蚀速率与浮箍开启角度的关系曲线,见图20。

图20 舌板式浮箍密封橡胶圈上冲蚀速率与浮箍开启角度的关系曲线Fig.20 Relationship curve of the sealing rubber ring erosion rate of the tongue floating hoop with the opening angle
由图20可见,总体上舌板式浮箍密封橡胶圈上的冲蚀速率随着浮箍开启角度的增加而减小,在浮箍开启角度达到50°时,浮箍密封橡胶圈上的冲蚀速率接近0。这是因为冲蚀密封橡胶圈的砂粒主要是经蝶阀阀板反弹的砂粒,砂粒的直径越大,惯性越大,受流体的影响就越小,经反弹的砂粒对浮箍密封橡胶圈的冲蚀作用就越强。
当含砂量为0.3%、砂粒直径为1 mm时,不同浮箍开启角度下舌板式浮箍舌板上和密封橡胶圈上冲蚀速率云图,见图21和图22。

图21 不同浮箍开启角度下舌板式浮箍舌板上冲蚀速率云图Fig.21 Cloud of the butterfly valve plate erosion rate of the tongue plate floating hoop with different opening angle

图22 不同浮箍开启角度下舌板式浮箍密封橡胶圈上冲蚀速率云图Fig.22 Cloud of the sealing rubber ring erosion rate of the tongue plate floating hoop with different opening angle
由图21和图22可见,随着浮箍开启角度的增加,舌板式浮箍舌板上和密封橡胶圈上的冲蚀速率显著减小,且浮箍密封橡胶圈上的冲蚀主要是由于部分砂粒经阀板的反弹作用于密封橡胶圈造成的;在浮箍开启角度大于或等于50°时,浮箍舌板上和密封胶圈上的冲蚀速率都变得非常小。
砂粒的直径和含砂量可以通过调整固控设备来控制,为了延长浮箍的安全使用时间,可以加强钻井液的固相控制。浮箍的开启度对冲蚀速率的影响最大,可以通过调整浮箍弹性装置的弹性系数,以满足在一定冲击力作用下浮箍的开启度要求。
通过上述分析可知,弹簧式浮箍在开启高度达到40 mm、舌板式浮箍在开启角度达到50°时,就浮箍的结构而言就能起到延长浮箍安全使用寿命的目的。
弹簧式浮箍阀芯蘑菇头在开启高度为40 mm时受到的轴向作用力为5 675 N,舌板式浮箍在开启角度为50°时受到的垂直于舌板的作用力为222 N,通过计算满足浮箍开启度的作用力条件,可为弹簧弹性系数的设置提供理论依据。
3 结论与建议
(1) 泥浆中砂粒直径越大对浮箍的冲蚀作用越严重,严格控制砂粒直径能够有效延长浮箍的安全使用时间。
(2) 泥浆中含砂量越高,对浮箍的冲蚀作用越严重,冲蚀速率与含砂量呈线性关系。
(3) 浮箍的开启度越大,冲蚀速率越小,弹簧式浮箍在开启高度L大于或等于40 mm,舌板式浮箍在阀板开启角度大于50°时,能使其冲蚀速率显著减小,可达到延长浮箍的安全使用时间的目的。

