强跟踪五阶CKF算法在初始对准中的应用

王律化,石志勇,宋金龙,王海亮

(陆军工程大学 石家庄校区七系，河北 石家庄 050001)

0 引言

惯性导航初始对准是确定初始导航参数的过程，分为粗对准和精对准两个阶段。精对准通过分析各个误差源对于对准结果的影响，进一步修正姿态矩阵。现阶段，精对准的研究主要集中在大失准误差模型和非线性误差模型的滤波算法方面。静基座条件下，系统误差模型主要是Φ和ψ的小角度误差模型，运用误差角为小角度的特点，可将误差模型进行线性化，满足线性卡尔曼滤波的要求，完成初始对准。随着载体机动性要求的提高，初始对准由静基座初始对准逐渐向行进间初始对准转化，小失准角的误差模型和线性的滤波方法已不能满足初始对准的要求。

本文针对载体行进间初始对准精度问题，在由里程计辅助惯性系统行进间精对准的情况下，推导了精对准误差模型，并建立了导航系统精对准的状态方程和量测方程。系统方程为非线性方程，系统状态的估计采用贝叶斯滤波方式，为提高滤波器在非白噪声条件下的鲁棒性，在计算贝叶斯滤波过程中的增益矩阵时引入自适应渐消因子。滤波过程中需要对于参量的后验概率密度进行数值解算，为提高解算精度，运用五阶球面-径向准则进行计算。仿真和实验结果表明，在方位角为大失准角的条件下，该算法可有效地保证较高的滤波精度，并且在噪声未知的情况下，滤波器保持很好的鲁棒性。

1 行进间捷联惯导系统初始对准误差模型

(1)

其中

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

取状态向量x=[φ(δvn) (δPn) (δPnD)bεbδKD]T，其中[]T为状态向量的转置。

噪声向量为

(11)

捷联惯导实测位置和里程计的实测位置的差值作为量测值

(12)

综上所述，行进间大方位失准角误差方程为

(13)

式(13)中f(x)的表达式具体见式(1)，其中状态噪声向量w和量测噪声v是零均值，方差为Q和R的高斯白噪声。量测矩阵为

(14)

2 贝叶斯滤波过程及其改进方法

2.1 贝叶斯滤波过程

处理式(13)的滤波方法一般为贝叶斯滤波。将式(13)进行离散化处理,则有

(15)

式中wk-1和vk是独立的状态高斯白噪声和量测高斯白噪声，其方差矩阵分别为Qk-1和Rk。

式(15)的贝叶斯滤波过程分为以下两步，即

1) 预测过程。

(16)

(17)

2) 更新过程。

(18)

(19)

(20)

(21)

(22)

(23)

贝叶斯滤波的预测和更新过程中，都涉及到如下形式的多维微积分：

(24)

对于式(24)的多维积分计算其解析解几乎不可能，一般是求解式(24)的近似数值解。根据近似求解的方法不同，将式(16)～(23)的滤波过程称为不同的滤波方法。根据容积近似计算方法[6]，系统噪声是高斯白噪声的情况下，可以对式(24)进行如下转换,即

(25)

式中:P=SST，S是P的平方根分解;NP为总采样点数；γi和Wi分别为采样点和采样点权重。

由式(25)的解算方法应用到式(16)～(23)得:

预测过程：

(26)

(27)

式中:Pk-1|k-1=SST;ξi=Sγi+k-1|k-1。

更新过程：

(28)

(29)

(30)

式(26)、(27)、(18)～(20)、(28)～(30)构成了贝叶斯滤波器数值解算的全部过程，式中Wi和γi的计算方法，则通过球面-径向准则进行计算。

2.2 强跟踪贝叶斯滤波过程

上述贝叶斯估计，要求系统的噪声是高斯白噪声，但是在实际的工作状态下，系统噪声的统计学特性是未知的，此条件下，使用贝叶斯滤波，使得系统的滤波效果变差甚至造成滤波器的发散。为提高滤波器的鲁棒性，同时，在噪声条件未知的情况下，保持良好的滤波精度。将强跟踪滤波(STF)和高阶容积滤波结合，在保证滤波精度的情况下，使滤波器的鲁棒性得到很好的提升。

将贝叶斯滤波过程的式(17)，(19),(20)进行等价变形得

(31)

(32)

(33)

式(31)中Fk,k-1是式(15)中f(xk-1)的离散化矩阵，表示从k-1时刻到k时刻的状态一步转移矩阵。

将次优渐消因子ηk代入式(31)中得

(34)

根据文献[9]中正交性原理的要求，ηk≥1，并且输出的残差序列为δk=zz-k|k-1，ηk的计算方法为

(35)

(36)

(37)

(38)

(39)

式中:tr[·]为矩阵迹的计算；ρ(0<ρ≤1)为修正系数，一般情况下ρ=0.95。在系统噪声未确定的情况下，运用式(40)解算系统噪声， 使系统噪声类似于高斯白噪声，从而便于进行解算。

3 五阶容积滤波解算方法

3.1 高维积分的数值计算准则

根据文献[11]，高维积分的数值计算为

(40)

式中：x=[x1x2…xn]T∈Rn；wg(x)g(x)的权重函数，g(x)=xα11xα22…xαnn，α1,α2,…,αn是非负整数，且α1+α2+…+αn≤d，d是所能达到的精度的阶数。

根据容积准则，形如式(24)的积分写成下列形式：

(41)

(42)

式(42)中主要涉及了两种形式的积分:

1) 径向积分，∫∞0gr(r)rn-1exp(-r2)dr积分的权重公式为：wg(r)=rn-1exp(-r2)。

2) 球面积分∫Ung(s)dσ(s)，对应的权重函数为：wg(s)=1。将径向积分和球面积分运用式(40)进行变形，式(42)可变为

(43)

式中:ri和wr,i分别为径向积分的采样点和采样点对应的权值；sj和ws,j分别为球面积分的采样点和采样点对应的权值。I(g)的总采样点为Nr、Ns，当ri中有一个采样点为0时，I(g)的总采样点数为(Nr-1)(Ns+1)。

3.2 五阶球面积分方法

根据文献[8]，形如IUn(gs)∫Ungs(s)dσ(s)的积分可以按照下式进行近似计算，即

(44)

式(44)为2m+1阶球面积分数值解算方法，式中IUn为被解算的函数。式中的权值函数和采样点的函数值之和分别为

(45)

(46)

根据文献[8],有如下公式：

(47)

式中:|k|=k1+k2+…+kn;Γ(z)是伽马函数，定义Γ(z) = ∫∞0exp(-λ)λz-1dλ。

当所要近似的积分阶数是五阶时，2m+1=5，则m=2。将结果代入式(45)中得

(48)

(49)

和

ws2所对应的采样点为ej和-ej，其中j=1,2,…,n。

将式(48)、(49)及采样点代入式(41)可得

(50)

3.3 径向积分法则

五阶及五阶以下的高维径向积分，可以使用高斯-拉格朗日积分法，但这个方法不能运用于五阶以上的数值解算，为提高径向高维积分解算方法的适用性，采用时矩匹配法解算径向积分。时矩匹配法具体表示为

(51)

因此，当运用时矩匹配法解算五阶径向高维积分时，得到如下方程：

(52)

式中Γ(z+1)=zΓ(z)，由于式(52)中有4个未知数，只有3个方程，同时为了保证采用时矩匹配法数值解算径向积分的采样点数最少，可以令r1=0，于是求得式(52)的解为

(53)

(54)

将式(42)、(51)、(53)、(54)代入式(24)中，运用五阶容积规则(Nr=2,Ns=2n2)解算得

(55)

4 仿真和实验

载体在完成行进间精对准的过程中，为了验证强跟五阶CKF算法对于载体状态的估计精度和估计时间，以及在噪声未知条件下的鲁棒性，通过和三阶CKF算法在系统误差模型确定的条件下，3个方向失准角的对比及在噪声条件未知的情况下，以航向失准角为例，对比强跟踪五阶CKF和三阶CKF的估计效果，说明强跟踪五阶CKF算法的估计精度和鲁棒性。

4.1 仿真实验

载体总的精对准仿真时间为600 s，假设载体的北向和东向初始位置分别为45.235 1°和85.268 4°，高为0，陀螺为激光陀螺，其常值漂移为0.015 (°)/h，随机漂移为0.001 (°)/h，加速度计常值零偏为450 μg(g=9.8 m/s2)，随机漂移为10 μg，里程计的刻度系数误差为2‰，载体在完成粗对准后的失准角为(3°，3°，10°) 仿真结果如图1～3所示。

图1 东向水平失准角

图2 北向水平失准角

图3 航向失准角

由图1～3可知，当失准角是小角度时，三阶容积滤波和强跟踪五阶CKF滤波的滤波效果相近。图3中，当失准角为大角度时，强跟踪五阶CKF滤波与3阶CKF滤波方式相比，其对于失准角的估计精度有所提高，就估计时间而言，由于强跟踪五阶CKF中径向积分采用时矩匹配法解算，与采用拉格朗日方程解算的三阶CKF算法相比，因其结构复杂，则收敛时间与三阶CKF相比为345 s，而强跟踪五阶CKF滤波在461 s后开始收敛，有着明显的滞后。

图4为非白噪声下的滤波。由图可知，当系统噪声不能看成高斯白噪声的情况下，由于不符合三阶CKF滤波的噪声假设，使得对于航向失准角的估计不能随着时间的推移而有所收敛，但是强跟踪五阶CKF滤波，由于引进了将次优渐消因子ηk，从而使有色噪声白化，使得最终的滤波效果可以收敛，从而实现最终的对准。

图4 非白噪声下的滤波

4.2 实车实验

实车实验采用装用GNSS/SINS/BD的组合导航系统的无人车(UGV)进行测试，采用高精度差分GPS所测量的路线作为路径真值，GPS的输出为1 Hz，定位精度为1 m。里程计的标度因数KD=0.035 45，定位精度度为0.05%(CEP)。实验过程中，无人车经过匀速直线、加速、左转、右转及减速等运动过程。整个运动时长是900 s。图5为实验用无人车。图6为实验路径。

图5 实验用无人车

图6 实验路径

以东向定位误差为例，对比实验过程中采用强跟踪五阶CKF算法和三阶CKF算法的定位误差。结果如图7所示。

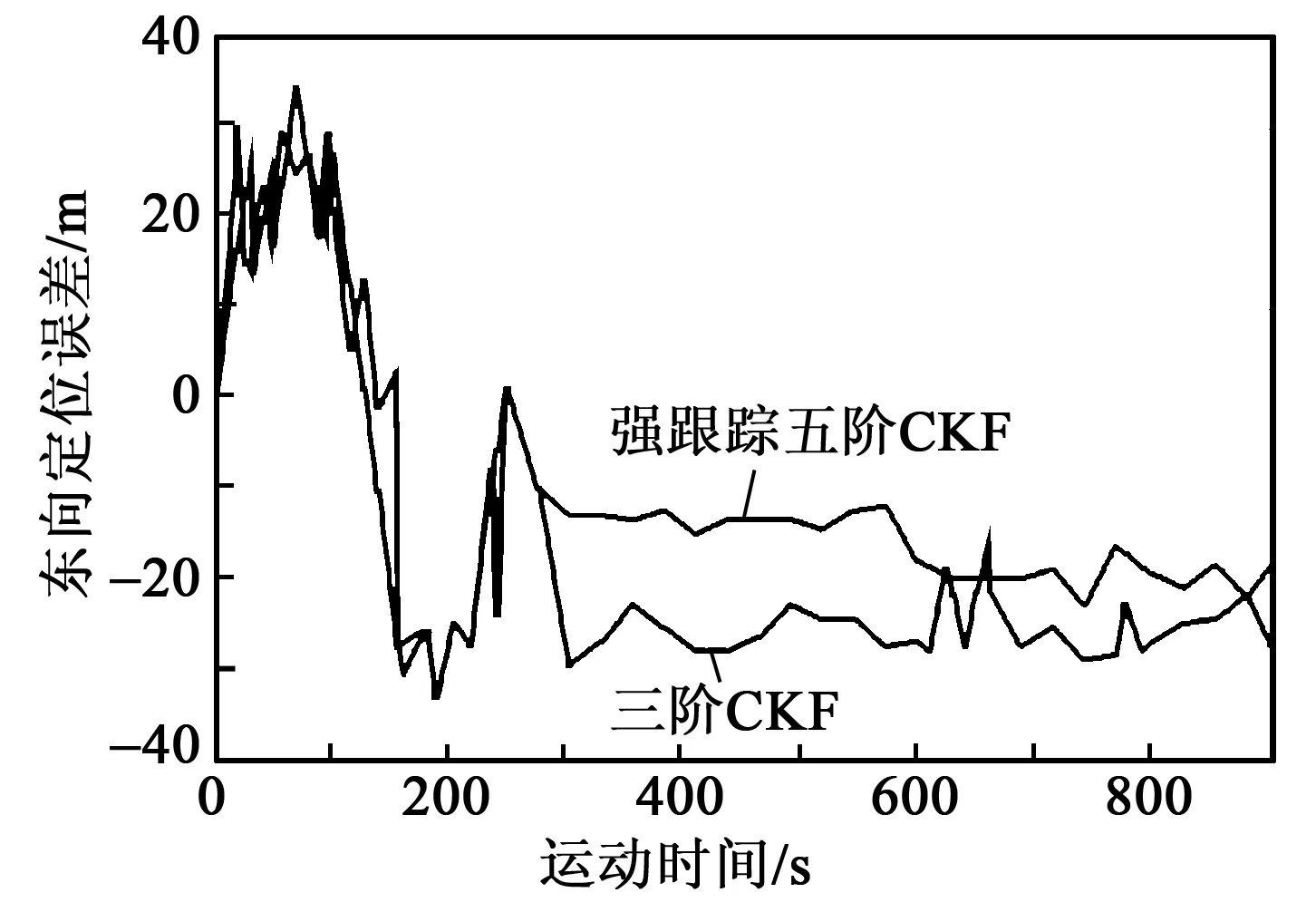
图7 定位误差对比图

由图7可知，当捷联惯导/里程计组合导航系统采用强跟踪五阶CKF滤波算法时，对比捷联惯导/卫星组合导航系统的输出结果的位置误差为20 m,当采用三阶CKF滤波算法输出的位置和捷联惯导/卫星组合导航系统输出位置做差，其结果为29 m，就东向定位精度而言，采用强跟踪五阶CKF滤波算法，其定位精度提高了31.1%。

5 结束语

通过对强跟踪五阶CKF滤波和三阶CKF的结果对比可知，载体采用强跟踪五阶CKF滤波方式估计载体行进间精对准的参数，与三阶CKF滤波方式相比，在时间上有所延长，其原因主要是采用五阶以上的计算方法，在计算点数增加，使得计算时间有所延长，但滤波精度和滤波器在非白噪声下的鲁棒性有着明显的提高，极大的增强了滤波器在非白噪声条件下的适用性。