大型高铁客运站到发线运用调整模型及算法
彭其渊, 宁 佳, 鲁工圆
(1. 西南交通大学 交通运输与物流学院, 四川 成都 610031; 2. 综合交通运输智能化国家地方联合工程实验室, 四川 成都 610031)
大型高铁客运站位于高铁网络的重要节点,通常衔接多条高铁线路并配备动车段;站内列车作业过程种类多样、运行进路及列车接续关系错综复杂,其车站作业对于所衔接各条线路的列车运行均有很大影响,且受到干扰后的决策质量可能影响多条线路的运营效率。为更好保障高铁网络中列车安全、有序运行,有必要重点研究大型高铁客运站的到发线运用调整问题。
大型高铁客运站到发线运用调整问题考虑在列车运行晚点或车站设备故障等干扰情况下,如何通过调整到发线运用方案及列车到发时刻,减小干扰对车站作业及列车运行的影响,以期尽快恢复正常秩序。该问题的解决方法需满足以下几个方面要求:
(1) 实时性要求 方法应能够在足够短的时间内得到调整方案;
(2) 可执行性要求 方案应能以尽量小的调整量尽快恢复车站作业及列车运行秩序;
(3) 安全性要求 方案应满足车站间隔时间、无进路冲突等安全要求。
纵观国内外学者关于到发线运用问题的研究,主要针对列车到发时刻确定条件下的到发线运用计划编制问题,而针对干扰情况下的到发线运用调整的研究相对较少。虽然两者在研究对象、优化目标和优化频次三个方面有所不同[1],但进路冲突疏解均为二者需要解决的一个关键问题,前者的既有研究成果具有一定的借鉴意义。文献[2]通过引入“时间片”的概念,简化到发线占用相容性约束,并设计最小最大蚂蚁算法求解。文献[3]将问题转化为加权节点包装问题,并利用分支定界算法求解。以上两篇文献均需预先计算出所有的相容进路集合,算法的复杂度随着问题规模的增大急剧增加。文献[4-5]将列车的接发车进路和到发线拼接成过站径路,考虑道岔和到发线的占用时间窗构造相容性约束,并设计模拟退火算法求解。文献 [6]通过构造列车作业时间窗冲突图,利用冲突识别、值排序以及BT搜索3个步骤进行求解。
以上文献均为针对到发线运用计划编制问题进行的研究,由于列车到发时刻固定,故在约束进路冲突时,均未考虑列车占用先后关系;另外,到发线运用实时调整要求算法收敛速度快,计算效率高,上述研究成果中所涉及的算法难以满足强时效性的要求。针对到发线运用调整问题,文献[1]提出了一种基于滚动时域的到发线动态调整策略;文献[7-8]采用模拟人工调度的方法,逐一为各列车安排到发线及接发车进路,并通过调整后行列车的到发时刻疏解冲突;文献[9]建立了2个线性规划模型,通过逐次求解两模型得到多个到发线调整方案,通过方案比选确定最终方案;文献[10]运用现代排序理论,设计自律优化算法及三步算法,实现股道运用的实时调整;文献[11]针对到发线异常下的咽喉区利用优化问题,通过引入“虚拟列车”,建立非线性优化模型,并设计遗传算法求解,但其计算效率仍无法满足实时性要求。
综上,目前针对干扰下的到发线运用调整研究较少,既有研究的有待完善之处主要体现在:干扰情况下,仅通过调整到发线可能无法实现冲突疏解,这时就需要对列车的到发时刻进行调整,而既有研究中绝大多数未考虑这一方面;既有调整算法难以满足实时性要求,且基于滚动时域和模拟人工调度的方法极有可能加剧晚点传播,难以保证求解质量;另外,大部分现有研究在构建进路冲突约束时仅考虑了一次解锁,缺乏针对不同解锁方式下进路冲突关系的统一性描述。
本文针对大型高铁客运站到发线运用调整问题,在将咽喉区进路和到发线组合成过站径路的前提下,首先,以列车实际到发时刻和过站径路选择为决策,构建混合整数线性规划模型,该模型可适用于不同的进路解锁方式;其次,将问题分解为到发线运用方案编制子问题和列车到发时刻调整子问题,分别设计分支定界算法和同步调整算法求解,并在此基础上提出了到发线运用调整优化的算法框架;最后设计算例对模型及算法的有效性进行验证。
1 到发线运用方案调整模型的建立
令某干扰情况下需要进行到发线运用方案调整的时间段(下文简称“调整阶段”)为[T0,Tn],列车集为K={1,2,…,n},列车按照在站作业方式的不同,分为始发列车、终到列车、通过列车、停站列车和立折列车[12]。不同类型的列车,在不同的进路解锁方式下,占用各轨道电路的起讫时刻不同。
为方便问题描述,本文从运输组织的角度,使用了如下占用时间的定义,即∀k∈K。

为便于模型构建,在保证模型对实际问题描述的准确性的基础上,对上述各时刻进行进一步预处理,这里分别以停站列车和通过列车为例进行说明,见图1,其他类型列车与停站列车类似,不再赘述。




所有的列车过站径路必须彼此相容,具体体现在以下两个方面:一是到发线占用相容性,即一条到发线同时最多只能被一列列车占用;二是咽喉区进路占用相容性,保证列车占用咽喉区进路时不能存在时空冲突。
文献[13]在考虑了列车占用先后关系的基础上,建立了敌对进路的疏解约束。文献[14]引入“冲突度”的概念计算不同解锁方式下的敌对进路解锁时间。令进路β与进路α的冲突度为γβ,α,则进路β开始占用γβ,α时间后,才能开始准备进路α的占用。在上述两篇文献的基础上,考虑不同类型列车接发车时占用咽喉区的开始时刻不同,∀k,h∈K,∀ρi∈Rk,∀ρj∈Rh,Rh={ρj|j=1,2,…,λh}(λh表示列车h的可行过站径路有λh条)令ωk表示列车k是否为通过列车,若是取1,否则取0,定义以下4类进路冲突度:

( 1 )

( 2 )

( 3 )

( 4 )
除此之外,对于∀k,h∈K,∀ρi∈Rk,∀ρj∈Rh,定义如下参数及0-1变量。

表1 模型0-1变量定义

表2 模型相关参数定义
到发线运用方案调整模型的约束条件如下:
(1) ∀k∈K,上述各占用时间的起讫时刻及实际到发时刻之间的关系如下
( 5 )
( 6 )
( 7 )
( 8 )
( 9 )
(10)
(2) 到发线相容性约束,对于∀k,h∈K,且k≠h,∀ρi∈Rk,∀ρj∈Rh
(11)
(12)
(3) 咽喉区进路占用相容性约束,对于∀k,h∈K,且k≠h,∀ρi∈Rk,∀ρj∈Rh:

(13)
(14)

(15)
(16)

(17)
(18)

(19)
(20)
(4) 径路可用性约束:以到发线故障为例,保证列车占用某条到发线时该到发线处于可用状态,即对于∀k∈K,∀ρi∈Rk
(21)
(22)
xk,i≤θk,i
(23)
(5) ∀k∈K,列车k的实际到达(出发)时刻不得早于图定到达(出发)时刻,且其在到发线上的停留时间不得少于最小停留时间要求,即
(24)

(25)
(26)
(6) 每1列车只能选择1条过站径路,即∀k∈K
(27)
在满足以上约束的条件下,模型的优化目标为:一是对车站作业秩序的影响最小,即尽可能少的调整到发线运用方案,并尽量满足到发线固定使用方案,其体现在尽量选择权重ck,i较大的径路,即
(28)
式中:ck,i为列车k选择径路ρi的权重。其值越大表示该选择对车站作业秩序影响越小,若与图定到发线运用方案相同,ck,i=1;若与图定方案不同,但符合到发线固定使用方案,ck,i=q1;若与图定方案不同,且不符合固定使用方案,ck,i=q2,0 二是列车总晚点时分最少,即 (29) 考虑到在现场实际中,当列车运行晚点或车站设备故障时,为避免列车晚点在路网中的传播,应优先考虑保证列车总晚点时分最少,故将上述双目标转化为单目标为 maxZ=Z1-αZ2 (30) 式中:α为一足够大的罚因子。该处理方法借鉴了文献[4]中的相关思路,以实现到发线运用调整方案中列车总晚点时分最少前提下对车站作业秩序影响最小的目标。 此目标函数保证了当列车运行晚点或车站设备故障时,为避免列车晚点在路网中的传播,优先考虑固定列车到发时刻不变,调整其到发线运用方案;若仍无法疏解径路冲突,再调整其到发时刻。这与现场生产中车站到发线运用调整逻辑相符。 上述所建立的模型为混合整数线性规划模型(MILP),模型中决策变量及约束条件的数目均较大,若直接利用优化软件求解,对于大规模算例,运算效率缓慢。这是由于每两条径路间均存在一组到发线相容性约束以及咽喉区进路占用相容性约束,这两组约束的存在是为了疏解径路冲突。考虑到径路冲突疏解的措施有以下两种:调整到发线运用方案以及调整列车到发时刻。为优先保证列车运行秩序,对于存在径路冲突的列车,首先考虑在列车到发时刻固定不变的前提下调整其到发线;若仍存在径路冲突,再对该部分冲突列车的到发时刻及到发线进行同步调整。基于此,将原问题分解为以下2个子问题: 子问题1 到发线运用方案编制子问题。在固定列车到发时刻的基础上,考虑到发线的固定使用方案、图定到发线运用方案、所有可行过站径路的可用性以及每两条径路间的相容性关系,制定总权重最大的过站径路选择方案。该子问题的模型M1如下 (31) 模型M1的最优解为具有相容过站径路且径路选择总权重最大的列车集。虽然模型M1总是有解的,但所得方案并不一定能实现调整阶段内所有列车的到发线分配,这时就需要对无法分配到发线的该部分列车集进行到发时刻调整,即子问题2。 子问题2 列车到发时刻调整子问题。在求解子问题1得到的径路选择方案的基础上,对无法分配到发线的该部分列车集进行到发时刻及到发线的同步调整,在保证列车总晚点时分最少的前提下,实现径路冲突疏解。该子问题的模型M2为 M2 式(29) s.t. 式( 5 )~式(27) (32) 可以看出,对于模型M1,列车到发时刻已知,其核心决策变量为径路选择0-1变量,各占用时间的起讫时刻可由径路选择方案及到发时刻综合决定,因此后文将设计高效分支定界算法进行求解;模型M2仅应用于仍存在径路冲突的部分列车集,求解规模较小,可直接利用商业优化软件求解。 基于此,下面将分别针对这两个子问题设计分支定界算法及同步调整算法进行求解,并在此基础上,进一步提出原问题的求解算法框架。 由于在子问题1中,列车到发时刻固定,则列车占用每条可行过站径路的相关起讫时刻也固定,进一步每条径路是否可用以及每两条径路间的相容性关系固定。 由于进路冲突度仅能描述咽喉区进路间的相容性关系,为进一步描述列车过站径路间的相容性关系,引入“径路相容性”:令ak,i,h,j表示列车k的径路ρi与列车h的径路ρj是否相容,相容取1,不相容取0。若两条径路存在到发线占用不相容或咽喉区进路占用不相容,即式(33)~式(41)中至少有一个成立时,ak,i,h,j=0;相反,若式(33)~式(41)均不成立,则这两条径路彼此相容,ak,i,h,j=1。 (1) 到发线占用相容性判定条件 (33) (34) (35) (36) (37) (38) (39) (40) (41) 若列车k的径路ρi不可用,则对于∀h∈K,∀ρj∈Rh,令ak,i,h,j=0,ah,j,k,i=0;另外,由于1列列车最多只能占用1条过站径路,结合后续算法的需要,令 (42) 为形象描述径路相容性关系,构建列车冲突图[14]:将所有的可行过站径路抽象为顶点v(如顶点vk,i表示列车k的径路ρi),相应的权重ck,i抽象为顶点权重ωk,i,径路间的相容关系抽象为顶点间的无向弧(当两径路相容时,对应两顶点间存在无向弧)。 类比顶点“度”的概念,引入顶点“权重度”:根据顶点vk,i与其他顶点的连接关系,若将该顶点入选完备子图(此时该子图仅包含这一个顶点),则完备子图可能达到的最大权重,称为顶点vk,i的权重度,记为udk,i,计算式为 (43) 子问题1转化为:在列车冲突图顶点的所有排列中,求其中具有最大权重的顶点集合,使得集合中任意两个顶点间有且仅有一条边。类比最大团问题(Maximum Clique Problem,MCP)[15],该问题具有以下特征:(1)顶点赋有权重;(2)目标为求具有最大权重的完备子图;(3)顶点与弧的数目均较多,但隶属于同一列车的顶点,最多只能有一个顶点入选可行解。下面将结合这些特征,设计分支定界算法。 通过对列车过站径路所做的特定选择构造一棵状态空间树,树的节点反映了对某一列列车的过站径路所做的特定选择。树的根代表了问题求解前的初始状态,第一层节点代表了列车1的径路选择方案,第二层节点代表了列车2的径路选择方案,以此类推。 令L表示状态空间树中存储的节点集合,L={P(Xp)|p=1,2,…},其中每一个节点均可表示为六元组P(Xp)=(dp,xp,up,UBp,Ep,Lp) up=∑vk,i∈xpωk,i (44) {ωh,j×min{ak,i,h,j|vk,i∈xp}|ρj∈Rh} (45) (46) 考虑到子问题1属于组合优化问题,状态空间树规模较大,传统的分支定界收敛较慢,为保证在不牺牲解的质量的前提下,提高算法的收敛速度,通过设置“前探”策略与“检查”机制,提出了一种高效的剪枝规则。改进后的分支定界算法流程如下: Step1初始步。计算该子问题的上界UB,计算式见式(47)。将x0初始化为空集,E0中每个元素初始化为1,产生根节点P(X0)=(0,∅,0,UB,E0,∅),则L={P(X0)},当前最优解x*=∅,u*=0。转Step2。 UB=min{max{udk,i|ρi∈Rk}|k∈K} (47) Step2选择节点。若L=∅,停止,x*为最优径路选择方案,u*为相应的总权重;否则,从L中选择具有最大深度、当前最佳、最有希望(即上界最大)的一个节点,记为PS(X)=(dS,xS,uS,UBS,ES,LS)。转Step3。 Step3分枝。在节点PS(X)的基础上,为列车(dS+1)选择径路,共产生(λdS+1+1)个节点,记LD={P(Xp)|p=1,2,…,λdS+1+1}。其中,对于∀p=1,2,…,λdS+1,节点P(Xp)表示选择径路ρp;而当p=λdS+1+1时,节点P(Xp)表示不为列车(dS+1)选择任何一条过站径路。转Step4。 Step4定界。计算集合LD中每一节点P(Xp)的dp、xp、up、UBp、Ep。对于每一个节点P(Xp): (2) 若dp=n,说明已搜索到一个可行解:若up>u*,说明up是比当前最优解u*更好的解,转Step5;否则,转Step6。 (3) 若dp (4) 若dp 待集合LD中每一个节点P(Xp)均计算、判断完毕,“检查”被选择节点PS(X),若其待检查节点集合LS≠∅,对LS中所有的待检查节点PS(Xg)进行遍历,转Step8。 Step5可行解。更新当前的最优解,即令x*=xp,u*=up,并从集合LD中移除节点P(Xp)。 若u*=UB,说明可行解x*与u*一定为该问题的最优解,停止;否则遍历集合L中的所有节点,∀P(Xf)∈L,若UBf≤u*,转Step6。 Step6剪枝。从集合LD中移除节点P(Xp),或者从集合L中移除节点P(Xf)。 (1) 若rh,j=rdp,p,则 (48) (2) 若rh,j=rdp,q,则 (49) (3) 若rh,j≠rdp,p,且rh,j≠rdp,q,则 (50) 将节点PS(X)从集合L中移除,令L=L∪LD,转Step2。 通过对子问题1的求解,可以得到列车到发时刻固定条件下对车站作业秩序影响最小的最优径路选择方案。若该方案实现了对调整阶段内所有列车的到发线分配,则原问题已得到最优解;否则,需要对仍存在径路冲突的列车进行到发时刻及到发线同步调整,以疏解径路冲突。 令通过求解子问题1,仍无法分配到发线的列车集合为K′。∀k∈K′,为疏解列车k与其他列车间的径路冲突,可能需要调整到发时刻及到发线的列车集合记为Jk,称为调整列车集。 同步调整算法流程如下: Step2合并调整列车集。∀k,h∈K′,且k≠h,若Jk∩Jh≠∅,则令Jk=Jk∪Jh,删除集合Jh。 Step3同步调整。对于集合J中每一个调整列车集,调用模型M2进行冲突疏解。由于每个调整列车集中包含的列车数目较少,模型的求解时间也较短。 通过上述讨论,将原问题分解为2个子问题,并分别提出了其求解算法。两个算法之间的联系如下:改进分支定界算法为同步调整算法生成无法分配到发线的列车集合,同步调整算法为改进分支定界算法更新径路相容性关系。原问题的求解步骤如下: Step1根据列车运行图信息、图定到发线运用方案、车站站型图、设备故障信息、到发线固定使用方案等,生成每列列车的可行过站径路集,并初始化每列列车占用每条径路的相关起讫时刻等。转Step2。 Step2调用改进分支定界算法求解径路选择方案。若该方案实现了调整阶段内所有列车的到发线分配,则已得到对车站作业秩序影响最小的到发线运用调整方案,且列车按照图定到发时刻运行,算法结束;否则,转Step3。 Step3根据Step2得到的无法分配到发线的列车集合,调用同步调整算法进一步疏解径路冲突。转Step4。 Step4更新每列列车的到发时刻,并重新计算径路相容性关系。转Step2。 以某大型高铁客运站为例,车站站型图见图2,共设有12条到发线,其中1~6道用于接发下行列车,7~12道用于接发上行列车。车站衔接A,B,C,D,E共5个方向,并配备有动车段。咽喉区进路采用分段解锁,假设所有列车均由基本进路接发,不考虑变通进路,则共有67条接发车进路,各进路占用时间取值由列车长度、列车速度及进路长度等因素综合确定。到发线占用最小安全间隔时间为180 s。车站10:00:00—12:00:00时段内到发84列高速列车,其中始发列车17列、终到列车14列、停站列车42列、立折列车11列。限于篇幅,各列车详细到发信息未予展示。 车站到发线运用计划的图定方案见图3。设置干扰场景包括以下3个干扰:(1)列车6晚点2 min到达;(2)5道在10:30:00—10:40:00时段发生故障,不可占用;(3)列车44晚点5 min到达。根据本文构建的模型及算法,在处理器为Intel Core i7 3.6 GHz、内存为16.0 GB的计算机上,运用C#编程,并调用CPLEX 12.6.3求解其中的模型M2,径路选择权重q1取0.8,q2取0.5,获得干扰场景下车站到发线运用调整方案见图4,图中每个矩形表示一列列车的到发线占用,水平方向的长度表示持续时间,矩形右边的数字表示列车编号,深颜色矩形表示产生到发线运用方案调整或者到发时刻调整的列车,浅颜色矩形表示没有发生任何调整的列车。对应的总权重Z1为81.9,列车总晚点时间为320 s,程序运行时间为1.33 s。 由图3与图4对比分析得:(1)由于列车44运行延误,导致其发车进路与列车47的发车进路产生时间冲突,为疏解冲突将列车47的停站时间延长120 s,同时为保证列车44与列车60先后占用2道的间隔时间不少于180 s,将列车60的到发时刻均向后推迟100 s。(2)由于5道在10:30:00—10:40:00时段内不可用,导致下行方向列车22和列车28被迫借用上行7道,进而迫使列车10与列车11交换到发线。列车22和列车28由于车站布置图的限制无法占用8道。(3)由于列车6运行延误,使得列车2被迫变更到发线至6道,进而导致下行方向列车5被迫借用上行7道。其余列车的到发线运用方案及到发时刻均保持不变。产生到发线运用方案调整或者到发时刻调整的列车见表3。可以看出,该调整方案满足实时性、安全性及可执行性的要求,且能优先保证列车运行秩序,通过调整到发线运用方案确保列车正点运行。 表3 干扰场景下列车信息调整汇总表 编号类型最小停站时间/s图定方案调整方案到达时刻出发时刻到发线停站时间/s到达时刻出发时刻到发线停站时间/s效用2下行34010:09:2010:15:00434010:09:2010:15:0063400.85下行14010:07:3010:09:50614010:07:3010:09:5071400.56下行12010:02:3010:04:30412010:04:3010:06:3041201.010上行94010:09:2010:25:00794010:09:2010:25:0089400.811上行34010:14:2010:20:00834010:14:2010:20:0073400.822下行45010:27:3010:35:00545010:27:3010:35:0074500.528下行12010:39:4010:41:40512010:39:4010:41:4071200.544下行42010:59:4011:06:40242011:04:4011:11:4024201.047下行36011:05:4011:11:40136011:05:4011:13:4014801.060下行27011:14:5011:19:20227011:16:3011:21:0022701.0 大型高铁客运站到发线运用调整具有实时性、可执行性、安全性等要求,干扰情况下如何快速生成调整方案以尽快恢复车站作业及列车运行的正常秩序,对于保障高铁网络中列车安全、有序运行具有重要意义。 针对该问题,本文在构建了到发线运用调整优化的混合整数线性规划模型的基础上,提出了一种基于分支定界的算法框架,其关键技术包括:(1)根据问题的特点,将问题分解为2个子问题,简化了问题的计算复杂度;(2)针对传统分支定界收敛速率问题,提出了一种基于“前探”策略与“检查”机制的高效剪枝规则;(3)通过构建列车冲突图,引入顶点“权重度”的概念,提出了一种高质量的上界计算方法,并以此改进了算法终止规则;(4)同步调整算法针对规模缩减的调整列车集,通过求解线性规划模型,实现到发线与到发时刻的同步调整。 算例分析表明:该算法能够有效解决到发线运用方案与列车到发时刻同步调整问题、不同进路解锁方式下的进路冲突疏解问题,并在上述前提下,快速生成随机干扰下大型高铁客运站到发线运用实时调整方案,所得方案与图定运用计划偏差较小,可操作性强。2 到发线运用方案调整模型的求解
2.1 模型的分解
2.2 分支定界算法







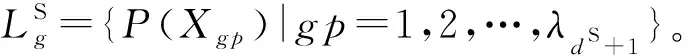

2.3 同步调整算法

2.4 到发线运用调整优化算法框架
3 算例分析




4 结束语

