根据给定的素材“烹饪”出精美的数学题
浙江省柯桥中学 (邮编:312030)
烹饪大师在一定时间内都能根据给定的素材烹饪出一道道味道好、色相好、营养好的菜肴,同样的食品素材经过不同大师的烹饪的菜肴不同,美食家们针对菜肴评价其烹饪水平,类似地,数学大师(教师)也应该在一定时间内根据提供的素材与要求创造出精美的数学题,这可以成为一种教学技能训练、教学水平评价、教学问题设计比武的方法,
德国物理学家海森堡说过:“提出正确的问题,往往等于解决了问题的大半”. 提出一个问题比解决一个问题显得更加重要,提出一个问题需要一个人具有敏锐的眼光、细致的观察、深入的思考.作为教师,不仅要会教学生解决问题,而且自己也应能够提出问题,创作出提升学生数学素养的问题.
1 函数性质示例
编题素材
(1)函数f(x)的奇偶性,周期性,零点;
(2)函数f(x)=2x+m,x属于某个单位长度区间内;
(3)f(2019)的值自定.
编制要求
(1)试题要涉及编题全部素材;
(2)设问目标与形式自定;
(3)试题必须具备准确性,创新性,试题阅读文字量(含符号)不超过100字;
(4)创作试题,给出解答,时间为40分钟.
测试目的
(1)检测应试者对函数“奇偶性,周期性,零点”概念的理解力;
(2)检测应试者具有一定的逻辑推理与运算能力;
(3)检测应试者的数学语言表达能力;
总之,以检测应试者的核心素养为基本点.
评价水平
(1)能够在熟悉的情境中,用归纳或类比的方法,发现数量或图形的性质,数量关系或图形关系;
(2)能够对与学过的知识有关联的数学命题,通过对其条件与结论的分析,探索论证的思路,选择合适的论证方法予以证明,并能用准确的数学语言表述论证过程;
(3)能够掌握常用逻辑推理方法的规则,理解其中所蕴含的思想,对于新的数学问题,能够提出不同的假设前提,推断结论,形成数学命题.
创作试题1
函数f(x)为R上奇函数,且满足f(1-x)=f(1+x),函数f(x)在[0,1]上的表达式为f(x)=2x+m.
(Ⅰ)如果函数f(x)在(2020,2021)内恰有一个零点,求实数m的范围;
(Ⅱ)如果f(2019)=0,试确定实数m的值.
解析函数f(x)为R上奇函数,则f(-x)=-f(x),又f(1-x)=f(1+x),所以
f(x+2)=f(1-(1+x))=f(-x)=-f(x),f(x+4)=f(x),即f(x)是周期为4的周期函数.
(Ⅰ)函数f(x)在(2020,2021)内恰有一个零点,根据周期性f(x)在(0,1)上恰有一个零点,于是f(0)f(1)<0,即(1+m)(2+m)<0,
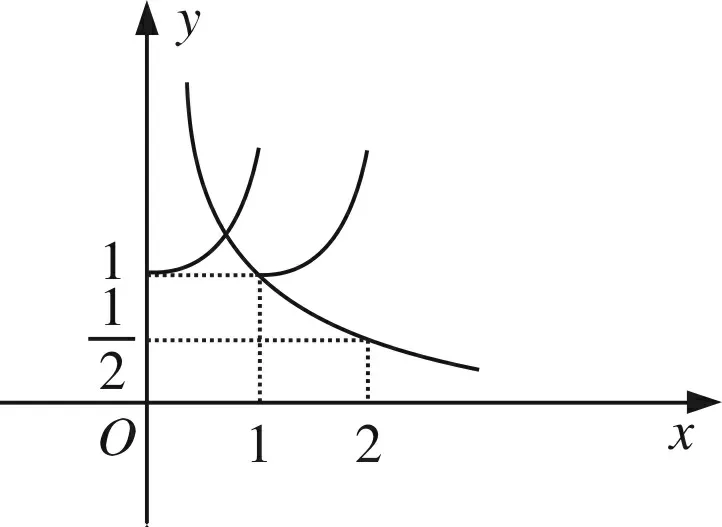
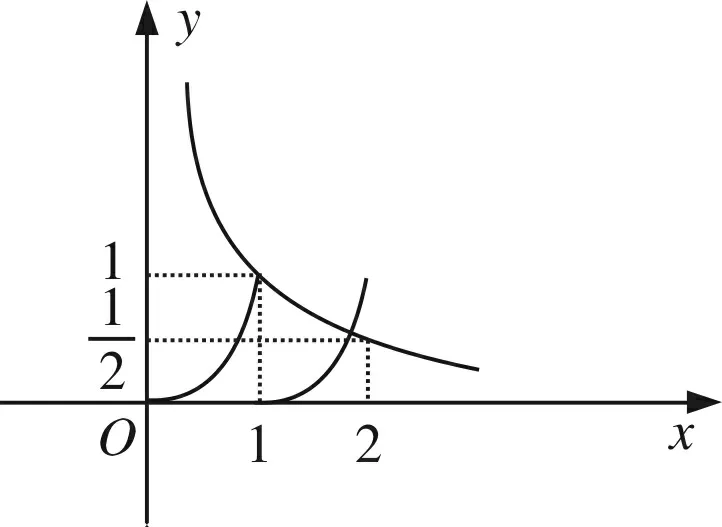
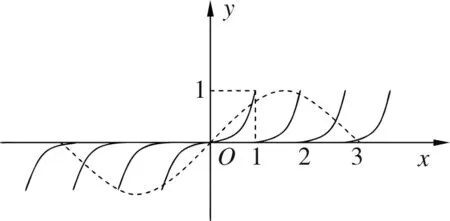
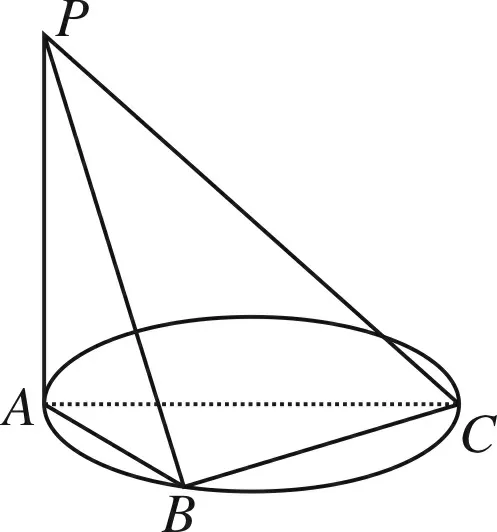
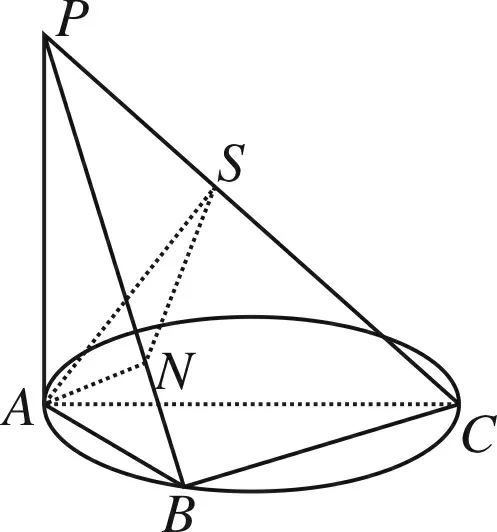
所以-2 (Ⅱ)f(2019)=f(3)=f(-1)=-f(1)=-(2+m),所以m=-2. 设计解读此题为检测高一学生在学习函数奇偶性、周期性、零点概念后的水平而设置,使其达到评价水平一:能够在熟悉的情境中,用归纳或类比的方法,发现数量或图形的性质,数量关系或图形关系. 创作试题2 函数f(x)为R上偶函数,且满足f(1-x)=f(1+x),函数f(x)在[0,1]上的表达式为f(x)=2x+m. (Ⅰ)若x=0是函数f(x)的一个零点,求f(x)在[2,4]上的表达式; (Ⅱ)若f(2019)=1,求f(1)+f(2)+…+f(2018)的值. 解析函数f(x)为R上偶函数,则f(-x)=f(x),又f(1-x)=f(1+x),所以 f(x+2)=f(1-(1+x))=f(-x)=f(x),即f(x)是周期为2的周期函数. (Ⅰ)因f(0)=0,即1+m=0,m=-1,x∈[0,1]时,f(x)=2x-1, x∈[-1,0]时,f(x)=f(-x)=2-x-1, x∈[2,3]时,x-2∈[0,1],f(x)=f(x-2)=2x-2-1, x∈[3,4]时,x-4∈[-1,0],f(x)=f(x-4)=2-x+4-1, (Ⅱ)f(2019)=f(1)=2+m=1,m=-1,f(x)在[0,1]上的表达式为f(x)=2x-1, 于是f(0)=0,f(1)=1,f(2)=0,f(3)=1,f(1)+f(2)+…+f(2018)=1009. 设计解读此题为高一期末考试而设计,检测学生综合理解函数的性质并学会分析的能力,使其具备评价水平二:能够对与学过的知识有关联的数学命题,通过对其条件与结论的分析,探索论证的思路,并能用准确的数学语言表述论证过程. 创作试题3 (Ⅱ)若函数f(x)为R上奇函数,求函数F(x)=f(x)-sinx,x∈[-π,π]零点个数. 解析 (Ⅰ)如图,当m>0时,不符合题意;m=-1时,不符合题意, 图1 图2 当m=0时,符合题意;当-1 (Ⅱ)函数f(x)为R上奇函数,所以f(0)=0,从而m=-1,f(x)的图象如图 图3 F(x)的零点个数为9个. 设计解读此题设计为利用数形结合思想解决数学问题的能力,适合高三数学复习检测,目的使学生达到评价水平三:能够掌握常用逻辑推理方法的规则,理解其中所蕴含的思想,对于新的数学问题,能够提出不同的假设前提,推断结论,形成数学命题. 编题素材 图4 (1)图1中的三棱锥形体结构称为“鳖臑(bie nao)——肩下谓之臂,臂下谓之臑(礼经释例·释牲)”,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC; (2)提出一个平面与平面垂直的证明; (3)提出一个直线与平面所成角的最值. 编制要求 (1)试题要涉及编题全部素材; (2)具体设问目标与形式自定; (3)试题必须具备准确性,创新性,试题阅读文字量(含符号)不超过150字; (4)创作试题,给出解答,时间为50分钟. 测试目的 (1)检测应试者的空间想象能力与逻辑推理能力; (2)检测应试者的运算能力; (3)检测应试者的数学语言表达能力, 总之,以检测应试者的核心素养为基本点, 评价水平 (1)能够在熟悉的数学情境中,借助图形的性质和变换(平移、对称、旋转)发现数学规律;能够描述简单图形的位置关系和度量关系及其特有性质; (2)能够在关联的情境中,想象并构建相应的几何图形;能够借助图形提出数学问题,发现图形与图形,图形与数量的关系,探索图形的运动规律; (3)能够在综合的情境中,借助图形,通过直观想象提出数学问题. 图5 创作试题4如图2,AC=2R为圆O的直径,∠PCA=45°,PA垂直于圆O所在的平面,B为圆周上不与点A、C重合的点,AS⊥PC于S,AN⊥PB于N, (Ⅰ)求证:平面ANS⊥平面PBC; (Ⅱ)设PB与平面PAC所成角为θ,求sinθ的最大值. 解析: (Ⅰ)平面ANS⊥平面PBC (Ⅱ)作BD⊥AC于D,连结PD, ⟹BD⊥面PAC,所以∠BPD为PB与平面PAC所成的角θ. (*) 即t2+(u-1)t+u=0,△=(u-1)2-4u≥0. 设计解读设计的问题中,面面垂直关系较多,选择证明的一对平面垂直关系可以将其他垂直关系一并带入,这是训练学生理解直线与平面垂直定义,直线与平面垂直判定以及平面与平面垂直判定的经典范例;所求直线与平面所成角的最值,引入参变量,建立目标函数,这样数学建模思想融入其中,最后求其最值的方法很多,限于篇幅这里只介绍一种.问题设计目的使学生达到评价水平二:能够在关联的情境中,想象并构建相应的几何图形;能够借助图形提出数学问题,发现图形与图形,图形与数量的关系,探索图形的运动规律. 根据给定的素材创作新的数学问题,对于数学教师不仅是一种教学能力,而且可以提升教师的数学素养,这样才能有效的落实培养学生数学素养的重任. 数学教学除了基本的教学理念之外,数学问题是数学教学的核心,然而“活而新”的问题才是取之不尽、用之不完的源泉,这应该是“教书匠”的基本功.它首先要求教师具有良好的数学语言(文字语言、图形语言、符号语言、关系语言)表达能力. 数学教师的解题能力,尤如家庭主妇天天要烹饪一日三餐一样;而限时编题能力尤如家中来客人,需要主人拿出一些特色美食招待客人,在一定时间内创造出符合学生认知,检测学生数学素养的数学问题并非易事,需要教师必须具备创新意识,创造能力,这才是真功夫. 在有限时间内教师创作的数学问题的水准,需要根据数学核心素养的评价标准,科学地加以评判,正象烹饪大师的作品也要经过美食家、营养家、评判专家的评判一样,虽然每个人的评价可能是模糊评判,但整体而言还是可信的,所以对于教师创造的数学问题,也可以用模糊评价方法实施.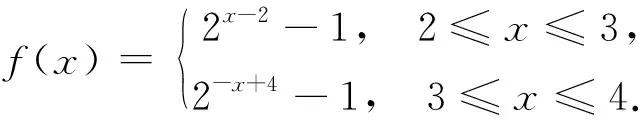
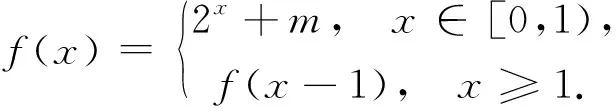
2 空间图形示例





3 作用
3.1 教学的基础性
3.2 功能的创新性
3.3 评价的科学性

