基于变长度单元ANCF的轴向伸展悬臂梁振动分析

王忠民， 吴力国

(西安理工大学 土木建筑工程学院， 西安 710048)

在工程实际中，轴向伸展悬臂梁系统被广泛的应用，例如装载车辆的伸缩构件，可伸缩的机翼，伸缩机器人操纵器，航天飞行器的伸缩附件等。这类系统的动力学方程的特点是时变和非线性的，并且系统的伸展运动和弹性大变形运动相互耦合。为了确保这些结构能够在稳定安全的工作条件下正常运行，对其动力学特性的研究至关重要。

1992年，Sivakumar等[1]分析了端部带有集中质量的伸展回缩悬臂梁的横向振动及其振动反馈控制问题。Stylianou等[2-3]采用了单元数量和节点不变、单元长度随着时间的改变的有限单元法分析了伸展悬臂梁的横向振动和稳定性问题，得出了梁在伸展过程中弹性振动稳定，但在回缩过程中不稳定。Al-Bedoor等[4]提出了一种改进的有限单元法，将轴向运动悬臂梁分为两段：支撑段假定成刚性体，悬臂段采用柔性体。将支撑体和悬臂段之间用一个变刚度的单元联接，并用有限单元法对悬臂段进行离散，得到系统的动力学方程。这样梁单元的数目和单元的长度均不改变，仅仅改变联接处的单元的刚度，但其过程非常复杂。Piovan等[5]采用有限单元法分析了沿轴向伸展和回缩的环形截面的功能梯度材料梁的振动问题，得到了在不同的伸展速率和不同的梯度指标下系统的动态响应数值解。Rogers等[6]采用了有限单元法分析了轴向运动为伸展和回缩弹性梁的横向振动问题，其方法是不改变梁单元的长度，梁单元的数量和节点随着时间改变而改变。Wang等[7]运用哈密顿原理研究了伸展黏弹性梁的横向弹性振动和轴向移动的耦合问题。Chang等[8]基于Rayleigh梁理论和Floquet理论，研究了悬臂梁在匀速运动和伸展回缩的周期运动运动下的横向振动和动力稳定性。罗炳华等[9]建立了轴向伸展梁受移动载荷作用的有限元模型，提出了描述运动梁节点约束状态的节点生死方法，计算了火炮炮口点处的横向动力响应。Downer等[10]提出了用变长度的有限元方法分析伸展梁的横向振动。Park等[11]根据von Karman非线性应变理论，推导了纵向和横向相互耦合的动力学方程，分析了当悬臂梁伸长或者回缩的过程中，其纵向和横向的振动响应。Yang等[12]分析了轴向回缩悬臂梁系统在回缩过程中的能量和等离子绝热不变量特性。赵亮等[13]应用广义哈密尔顿原理及假设模态法，导出了轴向运动功能梯度悬臂梁的动力学方程，分析了梁在伸展、收缩时的运动特性。杨鑫等[14]研究了两端简支不可移、轴向运动梁在热冲击作用下的横向振动特性。谭霞等[15]研究了外部激励作用下，超临界轴向运动Timoshanko梁横向非线性振动的稳态响应。

伸展悬臂梁系统中含有刚体运动和变形运动，本文采用Shabana提出的绝对节点坐标法[16](Absolute Nodal Coordinate Formulation，ANCF)，利用该法便于处理刚柔耦合大变形动力学问题的优点，建立了一种变长度的Euler-Bernoulli梁单元模型，并从大变形下准确的曲率和Green-Lagrangian正应变出发，基于考虑惯性力的虚功原理，得到了轴向伸展悬臂梁的单元非线性动力学方程组，以及组装后的伸展悬臂梁系统的非线性动力学方程组。最后，通过算例分析了材料特性参数(弹性模量、密度)和不同的伸展规律(匀速伸展、匀加速伸展)对伸展悬臂梁系统的末端非线性挠度响应的影响。

1 变长度绝对节点坐标法的单元描述

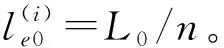
(1)

式中(·)=d()/dt。在图2中，对第i单元建立其自身的随体坐标系oxeye，任意一点p相对于oxeye和OXY的坐标分别为xe和X，单元i左端部相对于OXY坐标原点O的长度为Li(t)，有

Xi=Li+xe

(2)

点P相对于绝对坐标系在X方向上的速度为

(3)

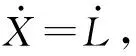
(4)

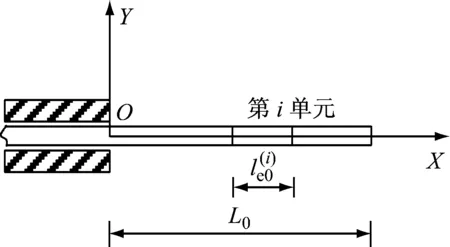
图1 初始瞬时的轴向伸展悬臂梁

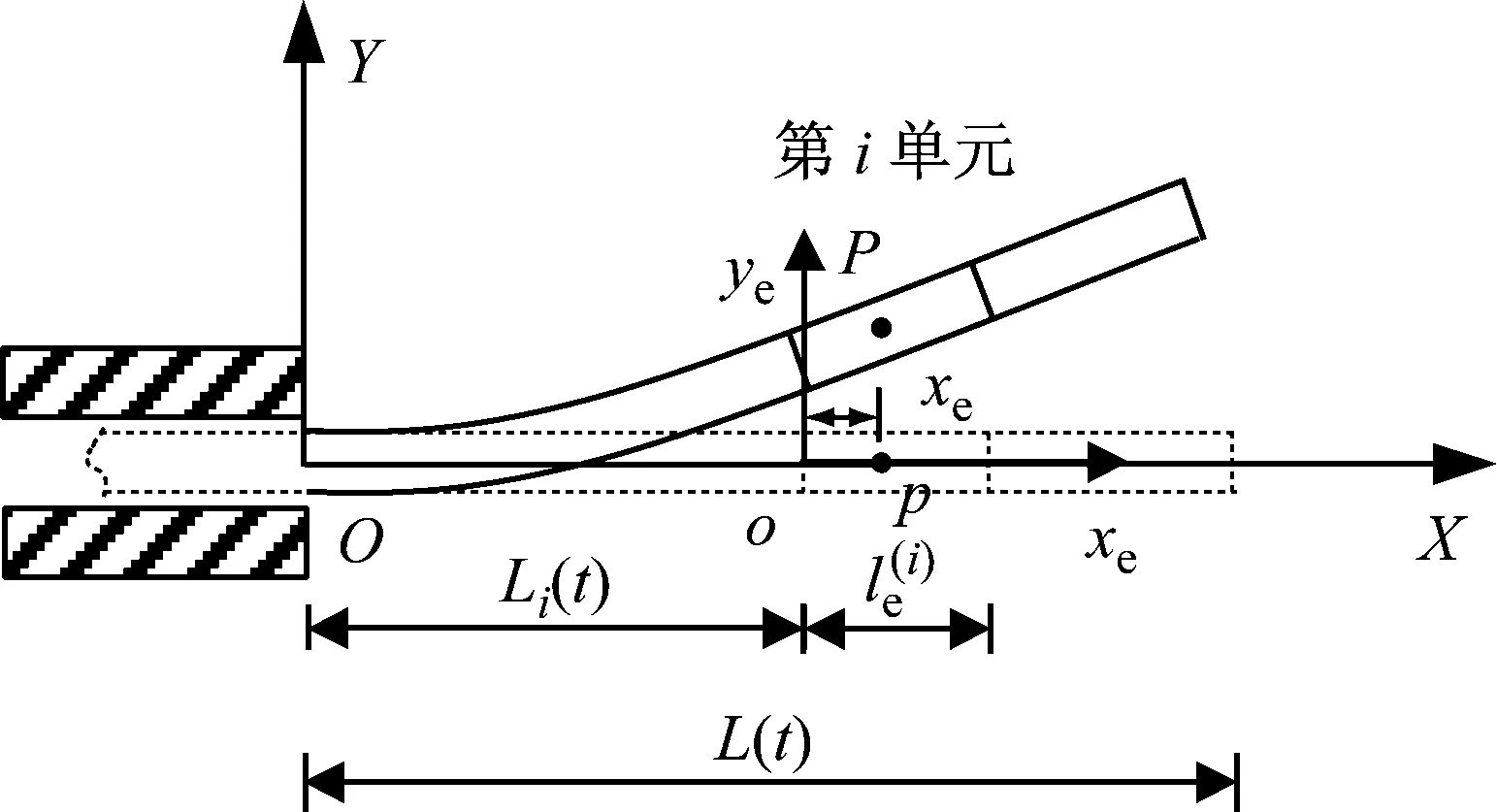
图2 任意瞬时的轴向伸展悬臂梁

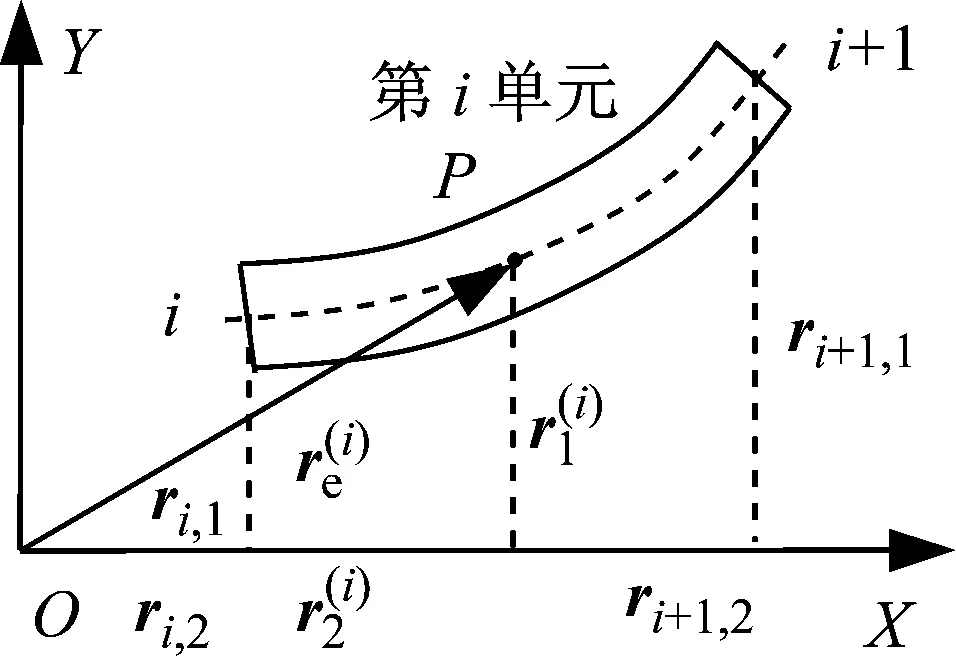
图3 变长度的柔性梁单元

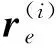
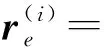
(5)

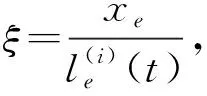
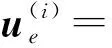
[e4i-3e4i-2e4i-1e4ie4i+1…e4i+2e4i+3e4i+4]

(6a)

Φ=[φ1(ξ)I2×2φ2(ξ,t)I2×2φ3(ξ)I2×2×

φ4(ξ,t)I2×2]

(6b)

(6c)

(6d)

2 变长度梁单元的非线性动力学方程

2.1 惯性力的虚功

值得注意的是，与传统的绝对节点坐标法不同，变长度单元的形函数矩阵与时间有关，即是时变的。将式(5)对时间t求一阶导数和二阶导数，得

(7)

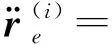
(8)

式中：

(9a)

(9b)

(9c)

(9d)

(9e)

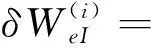
(10)

式中：

(11a)

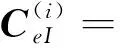
(11b)

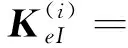
(11c)

2.2 弹性力的虚功

设梁单元的材料均匀和各向同性，根据Euler-Bernoulli梁理论和几何非线性理论，将梁的弹性力分为轴向应变产生的和弯曲应变产生的两部分。

梁单元的轴向Green-Lagrangian正应变为

(12)

梁单元由轴向产生的弹性力所做的虚功为

(13)

式中:

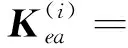
(14)

梁单元的准确的大变形曲率为

(15)

梁单元由弯曲应变产生的弹性力所做的虚功为

(16)

式中:

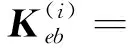
(17)

3.3 外力的虚功

在绝对坐标系下，梁单元上任意一点的均布体力向量为F=[0 -ρg]T，重力(体力)做的虚功为

(18)

梁单元受到的广义均布重力的表达式为

(19)

2.4 变长度伸展梁单元无约束非线性动力学方程

根据弹性体的虚功原理知，变长度梁单元的惯性力、弹性力、广义外力所做的虚功有

(20)

把式(10)、(13)、(16)和(18)代入式(20)，得到变长度伸展梁单元的无约束非线性动力学微分方程组

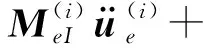
(21)

3 伸展悬臂梁系统的动力学方程组

为了得到伸展悬臂梁系统的动力学方程组，需要对划分的变长度梁单元进行组装。若将伸展悬臂梁划分为了n个单元，那么总共包含n+1个节点，每个节点包含四个广义位移分量。令u为伸展悬臂梁的整体位移列阵

u=[e1e2e3e4…e4n+1e4n+2e4n+3e4n+4]T

(22)

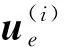
(23)

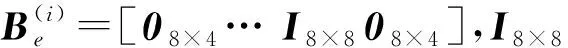
伸展悬臂梁上的惯性力做的总虚功为

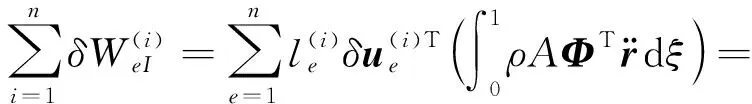
(24)

式中:

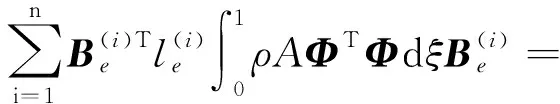
(25a)

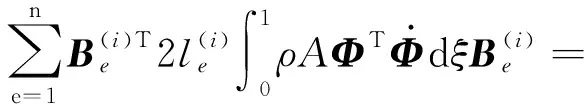
(25b)

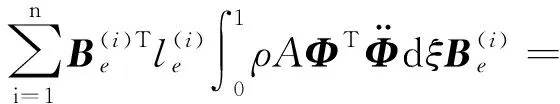
(25c)

同理得到

(26)

(27)

组装后的伸展悬臂梁系统的非线性动力学方程组为

(28)

该系统的约束方程可写为P(u,t)=0，即e1=e2=0,e3=1,e4=0。引入拉格朗日乘子λ，伸展悬臂梁系统的非线性动力学方程组为

(29)

式中：Pu为约束的Jacobi矩阵。

方程(29)的系数方阵中包含有时间和u，所以伸展悬臂梁系统的动力学方程是时变的非线性动力学方程，或化为关于时间的微分代数方程组。利用龙格—库塔法求解时变系数的微分代数方程组。

4 数值计算与分析

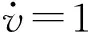
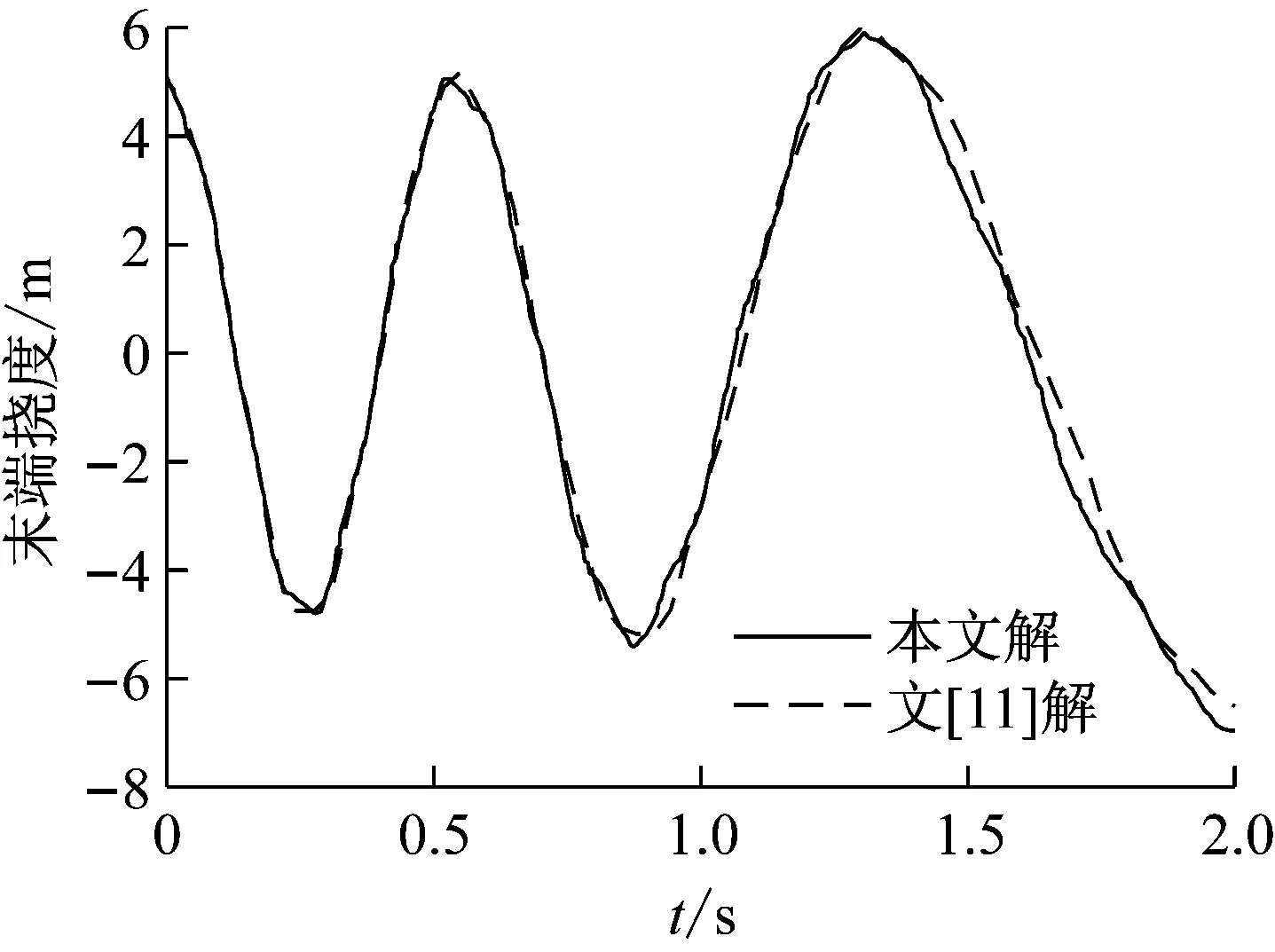
图4 匀加速伸展悬臂梁末端挠度响应

4.1 材料特性参数对匀速伸展悬臂梁末端挠度响应的影响

悬臂梁作伸展运动时，伸展长度遵循一定的规律，即可以按着匀速运动的规律伸展，也可以按着加速、指数、正弦或其他规律伸展。由于系统的动态特性受很多方面的影响，下面分析材料的性能参数(密度、弹性模量)和伸展规律(匀速、匀加速)对伸展悬臂梁末端非线性挠度响应的影响。

参数选取为：横截面面积A=1.6×10-3m2，惯性矩I=2.133×10-7m4，匀速伸展规律为L=L0+vt=0.9+0.4t(m)，初始时刻末端的挠度值为0.009 6 m。

在弹性模量E=1.4×109Pa下，分别选取材料质量密度1 770 kg/m3和1 040 kg/m3，计算的匀速伸展悬臂梁末端挠度响应如图5所示。由图可知，在伸展时间4 s内，材料密度较大的伸展悬臂梁末端挠度最大值稍大一些，但密度较小的伸展悬臂梁末端响应的振动频率较大，即伸展结构越轻，将使伸展悬臂梁的末端横向振动频率增大。

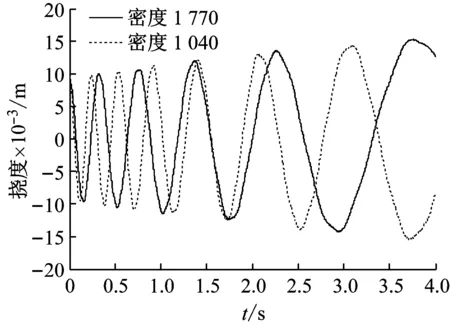
图5 材料密度对匀速伸展悬臂梁末端挠度响应的影响

在材料密度ρ=1 770 kg/m3下，分别选取弹性模量E=8.3×109Pa和E=1.4×109Pa，图6给出了弹性模量对匀速伸展悬臂梁末端挠度响应的影响。从图可以看出，在伸展时间4 s内，两者的末端挠度最大值相差不大，但弹性模量较大的伸展悬臂梁末端挠度的振动频率较大，即增大材料的弹性模量，相当于增大了系统的刚度，故频率增加。

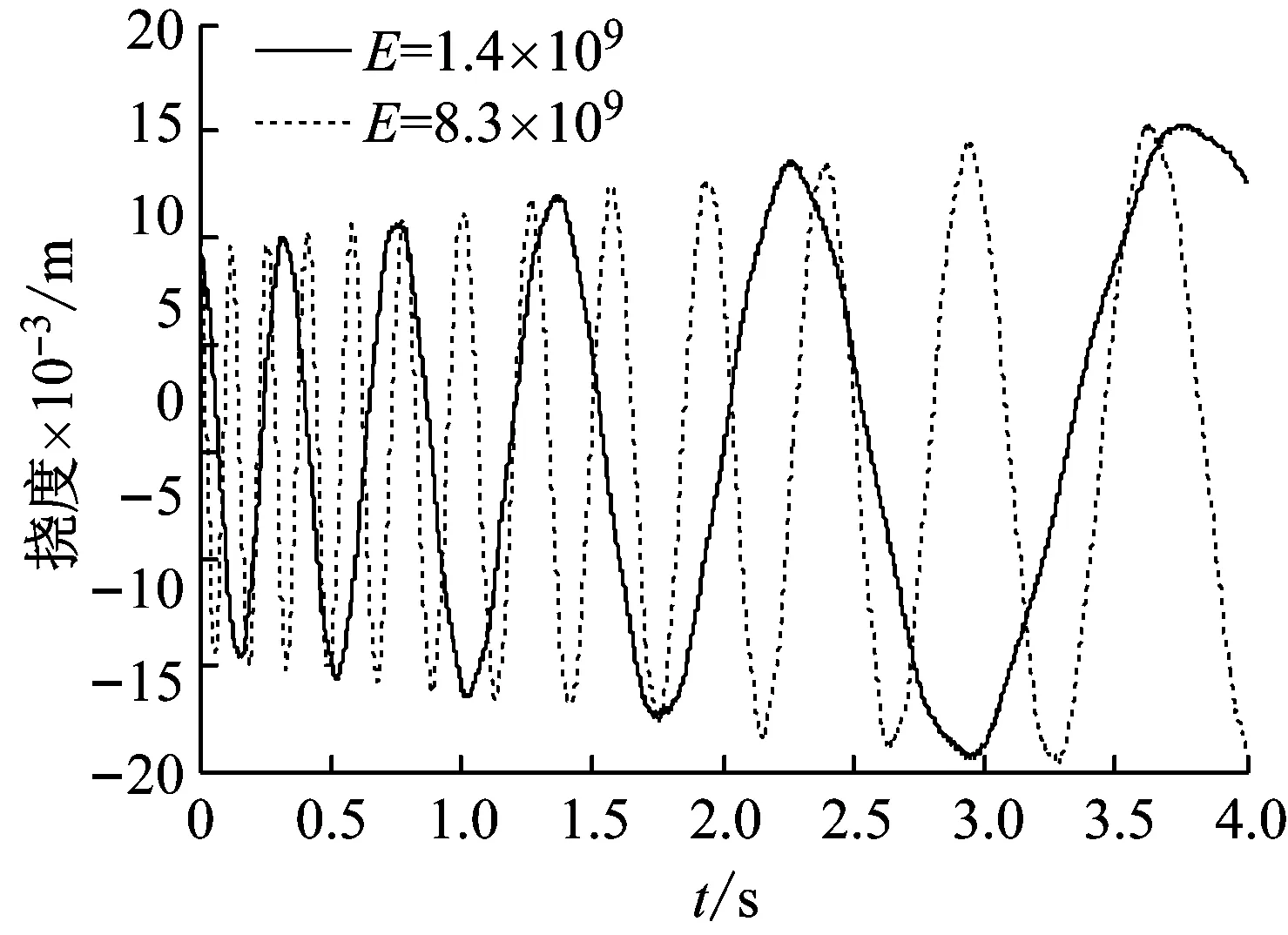
图6 弹性模量对匀速伸展悬臂梁末端挠度响应的影响

4.2 速度和加速度对伸展悬臂梁末端挠度响应的影响

选取质量密度ρ=1 770 kg/m3，弹性模量E=1.4×109Pa。悬臂梁以v=0.2 m/s和v=0.4 m/s的常速度匀速伸展，末端非线性挠度响应如图7所示。从图可以看出，在伸展时间4 s内，较大的伸展速度导致悬臂梁的末端最大挠度值较大，但振动频率小于低速伸展悬臂梁的振动频率。所以，当悬臂梁以不同的速度伸展相同长度时，低速伸展的悬臂梁，其末端横向振动的频率较大。

对匀加速伸展的悬臂梁，设其伸展规律为L(t)=0.9+0.5at2，即初始长度为0.9 m，以加速度为a作匀加速伸展。伸展加速度为a=0.1 m/s和a=0.2 m/s时得到伸展悬臂梁的末端挠度响应如图8所示。由图可知，在初始瞬时范围内，以不同加速度伸展的悬臂梁的末端挠度响应几乎相差不大，但随着时间的增加，悬臂梁的末端挠度值都在增大，且较大加速度伸展的悬臂梁末端挠度大于较小加速度挠度值。较大加速度伸展的悬臂梁的末端振动频率要小于较小加速度伸展的悬臂梁的末端振动频率。

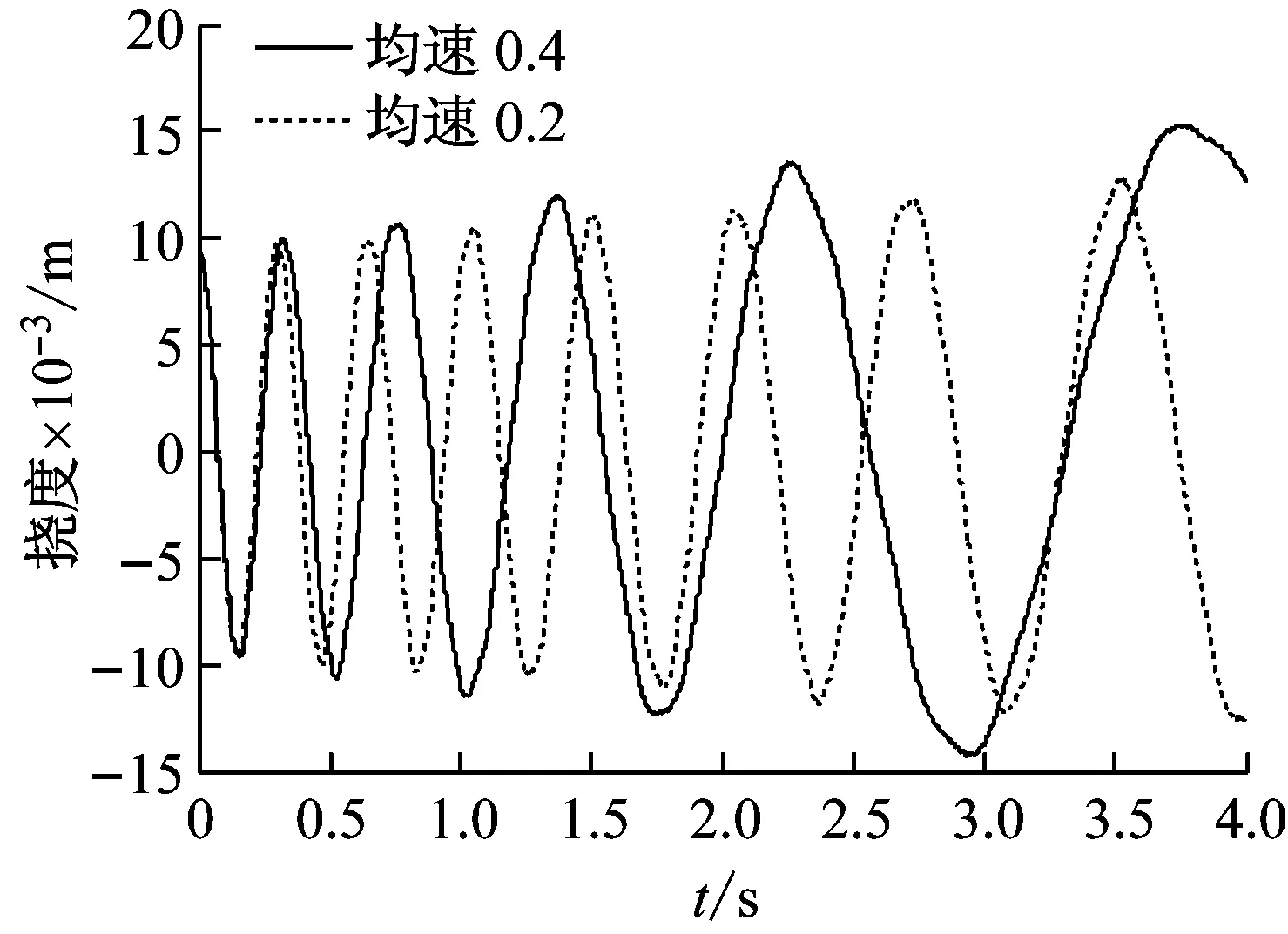
图7 不同匀速伸展速度下悬臂梁末端挠度响应

悬臂梁分别以速度为v=0.4 m/s匀速伸展和以加速度为a=0.2 m/s2匀加速伸展的末端挠度响应如图9所示，在t=4 s时，悬臂段长度均为2.5 m，前者的在4 s伸展时间内，悬臂梁的末端最大挠度较大，但悬臂梁匀速伸展时其末端的振动频率要小于匀加速运动规律伸展的情况。

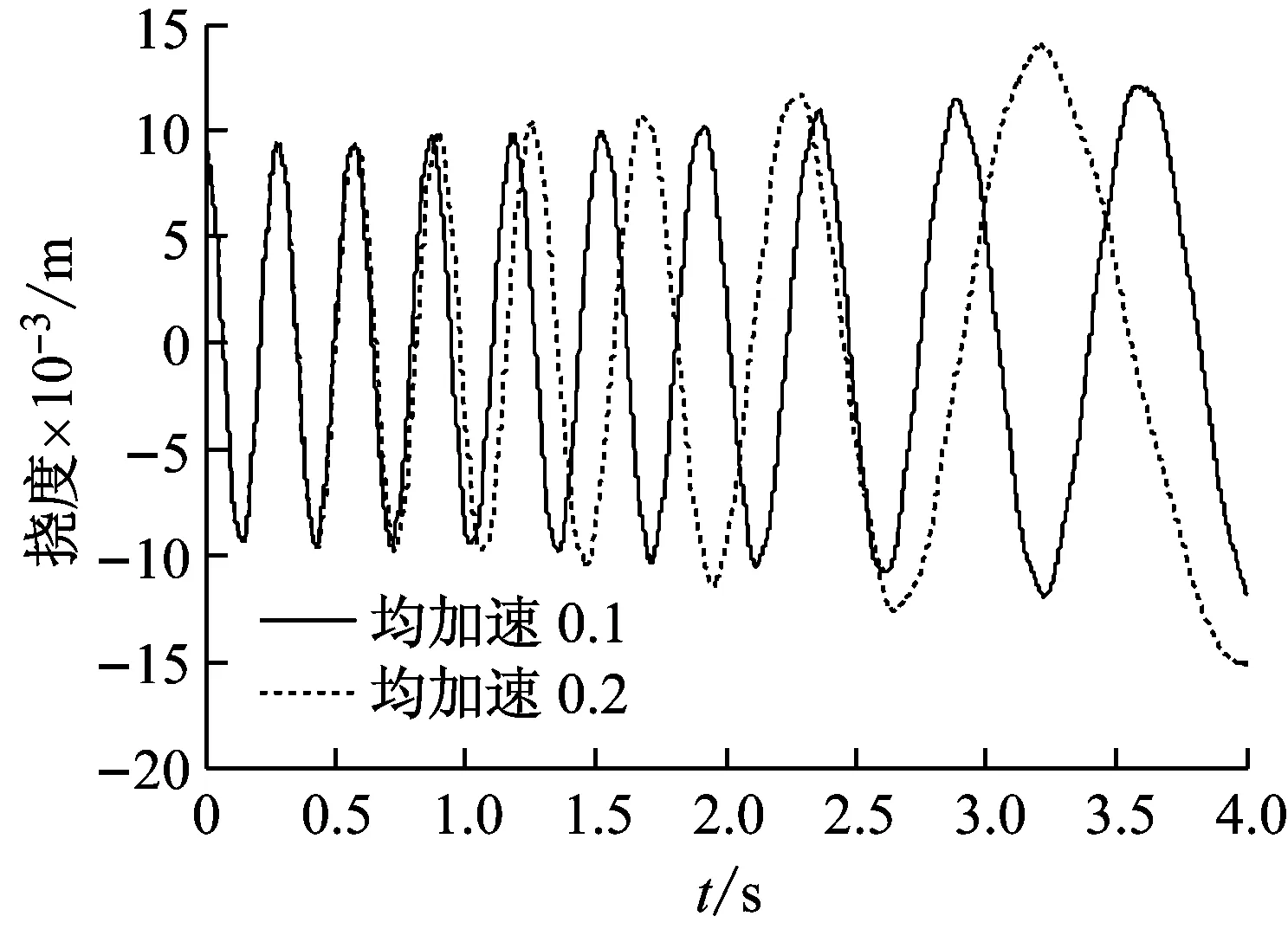
图8 不同加速伸展时悬臂梁末端挠度响应

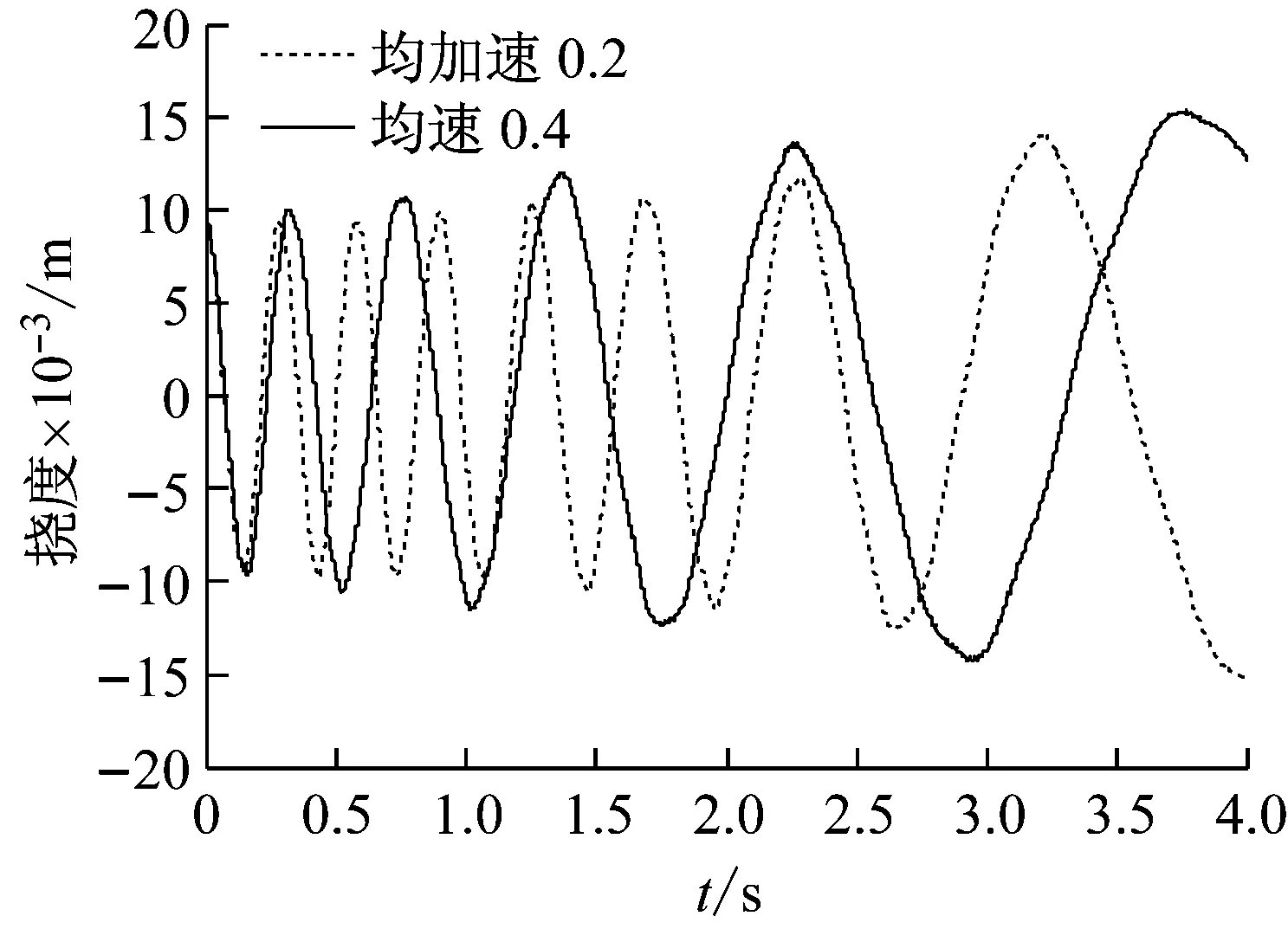
图9 不同伸展规律下伸展悬臂梁末端挠度响应

5 结 语

(1) 采用变长度单元的ANCF建立了伸展悬臂梁刚柔耦合系统的非线性动力学模型，与已有算例的结果比较说明了该法的可行性和有效性。

(2) 在匀速伸展条件下，弹性模量和质量密度均对伸展悬臂梁的末端挠度响应有影响，当材料的弹性模量越大和材料较轻时，均使得伸展悬臂梁的末端振动频率增大。

(3) 对匀速伸展的悬臂梁，较大的伸展速度导致悬臂梁的末端最大挠度值较大，但振动频率小于低速伸展悬臂梁的振动频率。对匀加速伸展的悬臂梁，较大加速度伸展的悬臂梁末端挠度大于较小加速度挠度值，但前者的振动频率要小于后者。