一种曲面-弹簧-滚子机构的非线性隔振器特性分析

韩俊淑， 孙景工， 孟令帅

(军事医学科学院 卫生装备研究所，天津 300161)

本文设计了一种曲面-弹簧-滚子机构的准零刚度非线性隔振器，如图1所示，该机构采用曲面-弹簧-滚子获得负刚度，具有承载力大、结构尺寸小、简单实用等特点。文中对所设计的隔振器开展了动态特性研究，针对系统平衡点不在隔振器最小刚度点的情况，研究了最小刚度分别为零刚度与正刚度时，不同激励幅值、偏移量、阻尼比条件下的系统动态特性，并开展了相关实验验证研究。

1 隔振器模型

1.1 曲面-弹簧-滚子隔振器

如图1所示，所设计的曲面-弹簧-滚子机构包括竖直弹簧1、水平弹簧2、支架3、滚子4及曲面座5等。曲面座与车厢地板或其他基座相连，支架用于支撑载质量且随竖直弹簧上下运动，滚子可在曲面座轨道内上下滚动，假设滚子与曲面座始终处于接触状态。图1(a)、(b)所示分别为该机构处于初始位置和平衡位置的状态，当机构处于平衡位置时，滚子与曲面座的曲面顶点接触，机构各参数如图中所示，kv为竖直弹簧刚度；kh为水平弹簧刚度；uv为竖直弹簧预压缩量；uh为水平弹簧预压缩量。

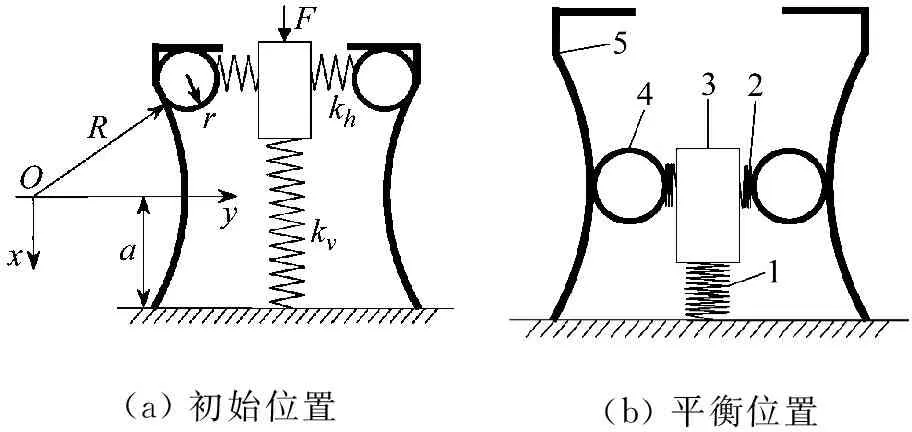
(a) 初始位置(b) 平衡位置

图1 非线性隔振器的结构示意图

Fig.1 The schematic representation of the nonlinear vibration isolator

建立如图1(a)所示坐标系，设滚子初始位置球心坐标为(x0,y0)，滚子在曲面座轨道内向下滚动到任意位置(x,y)，根据受力平衡，得到被隔振物体在竖直方向的力和位移的关系：

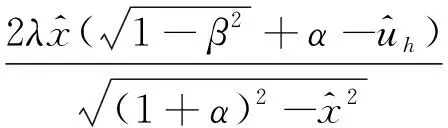
(1)

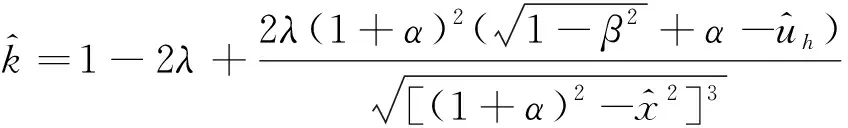
(2)

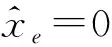
(3)

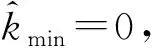
(4)

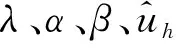
1.2 系统回复力近似

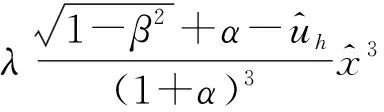
(5)

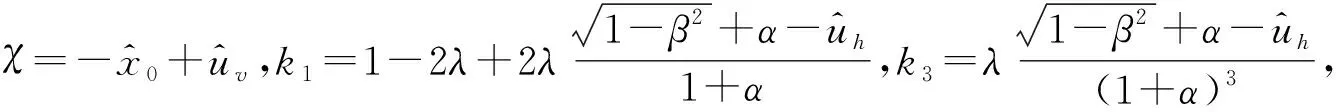
(6)

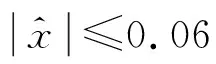
2 动态特性分析

2.1 动力学模型的建立

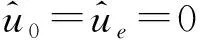
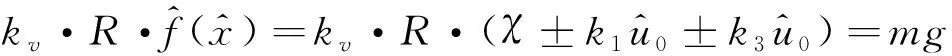
(7)

式中：“-”代表欠载状态。

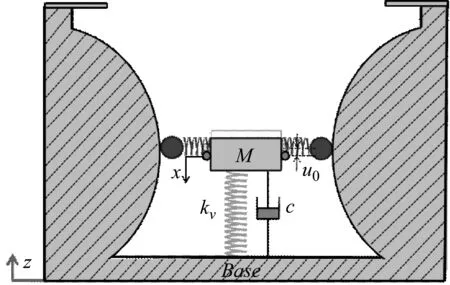
(a) 过载状态

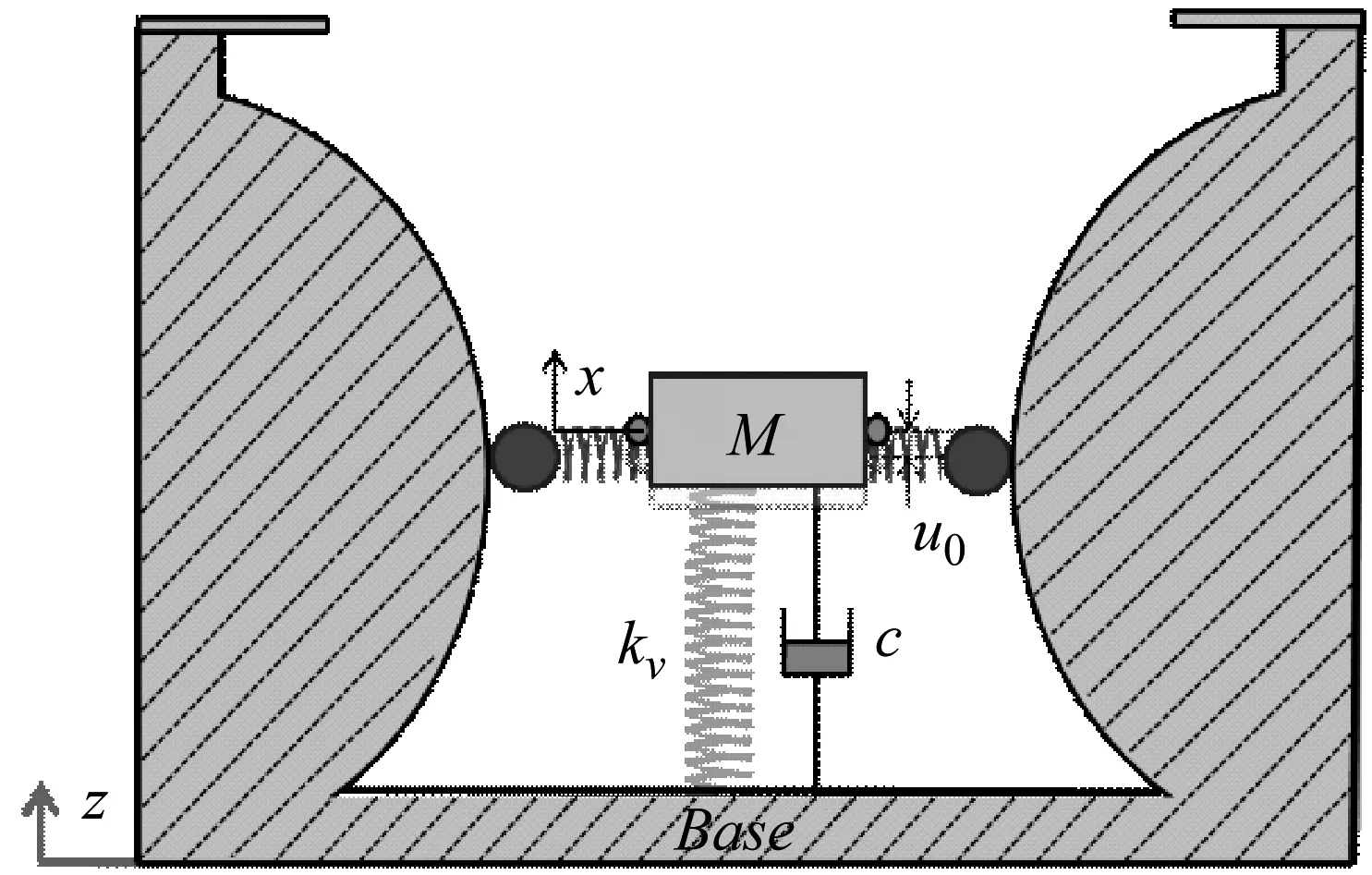
(b) 欠载状态

假设系统在过载或欠载条件下达到静力平衡后，受到来自基座或车厢地板的谐波位移激励z=Z0cos(ωt)，根据牛顿第二定律，建立系统非线性运动微分方程为：

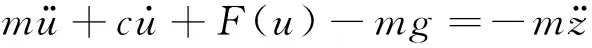
(8)

得到系统的无量纲近似稳态运动微分方程为：

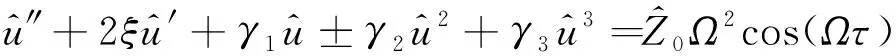
(9)

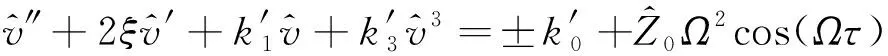
(10)

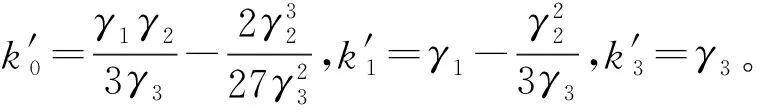
采用谐波平衡法对上式求解，设该稳态响应解的形式为：

(11)

式中：A0、A1分别为稳态响应解的常数项及谐波项幅值。

将式(11)代入式(10)，忽略高次谐波项，并令相同类别的谐波项系数及常数项相等，得到系统稳态条件为：

(12a)

(12b)

(12c)

由式(12b)、(12c)方程两边求平方和，可得系统幅频响应函数为：

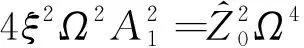
(13)

联立式(12a)、(13)，可得到关于A0的隐函数方程：

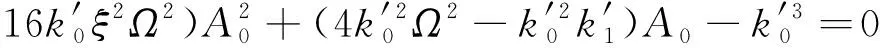
(14)

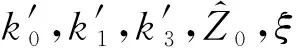
去掉负刚度机构，可以得到与之对应的等效线性系统，其无量纲运动微分方程为：

(15)

该等效线性系统稳态响应幅值为

(16)

2.2 定义传递率

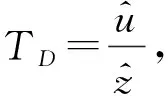
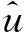
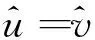
则系统绝对位移传递率表达式为：

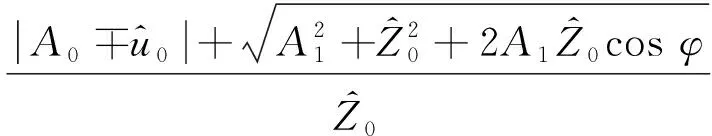
(17)

绝对加速度传递率为系统响应无量纲绝对加速度幅值与无量纲激励幅值的比值，即

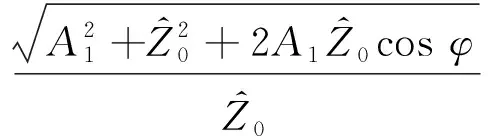
(18)

可以看出，过载或欠载系统绝对位移传递率必大于其绝对加速度传递率。

对于等效线性系统，绝对位移传递率与绝对加速度传递率具有相同表达式，分别为

(19)

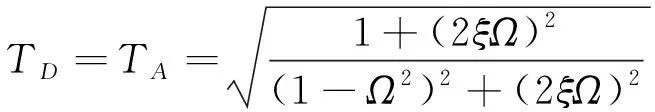
(20)

以上各式中cosφ可由式(12b)得到。

2.3 最小刚度为零时的特性分析

当系统最小刚度为零，即前文所建立的隔振器动力学模型中k1=0，可得过载(欠载)状态下的系统近似稳态动力学方程为：

(21)

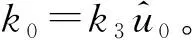
采用谐波平衡法对上式求解，可得系统幅频响应函数及常数项与谐波项幅值的隐函数方程[19]。设式(21)稳态响应解为式(22)的形式，其中δ(τ)为解的微小扰动量。

(22)

将其代入式(21)，略去高阶扰动量，并设δ(τ)=σ(τ)e-st，简化后得到

6k3A0A1cos(Ωτ+φ)+

(23)

于是，根据Floquet理论，可得系统稳定性条件为：

b0(b0-Ω2)2>0

(24)

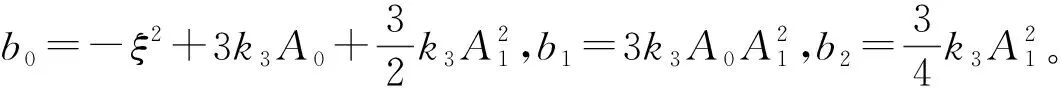
当Δ>0时，系统稳定，否则系统不稳定，由此即可得到系统不稳定解(各图中不稳定解以虚线表示)。

表1 谐波位移激励条件下的参数取值

由传递率曲线可知，过载系统的绝对位移传递率永远大于其绝对加速度传递率。在谐波位移激励下，随激励幅值增大，过载系统绝对位移和加速度传递率峰值及与之对应的共振频率均先减小后增大，当激励幅值增大到一定值时，过载系统传递率峰值会出现无限大值，系统隔振性能变差。同一激励条件下，随偏移量增大，过载系统传递率曲线向左或先向左后向右偏，传递率峰值增大。随阻尼比增大，三个系统在共振频率附近的区间内，传递率峰值减小，相应的共振频率先减小后增大，高频区域内各系统传递率增大，高频隔振性能下降。

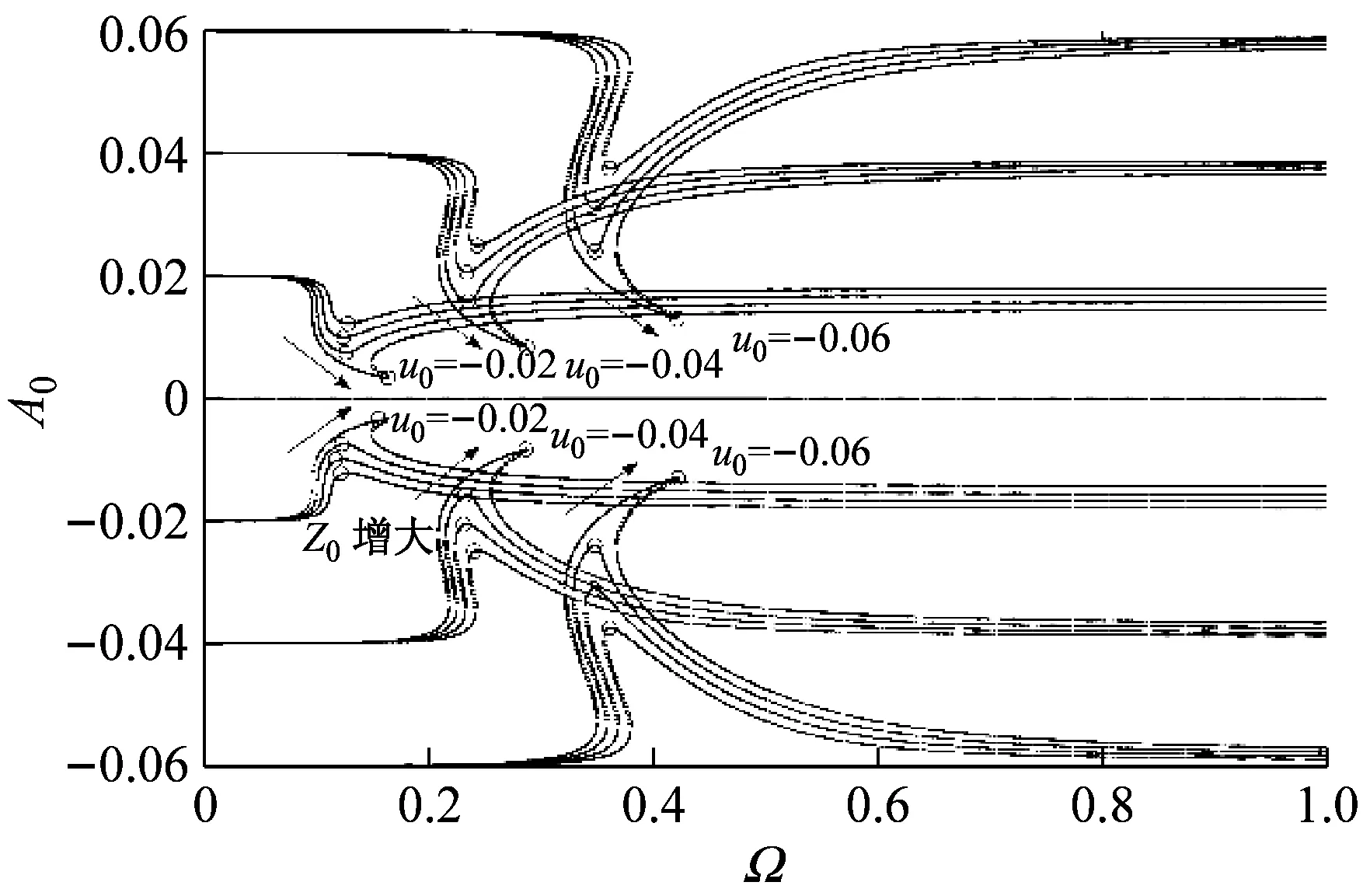
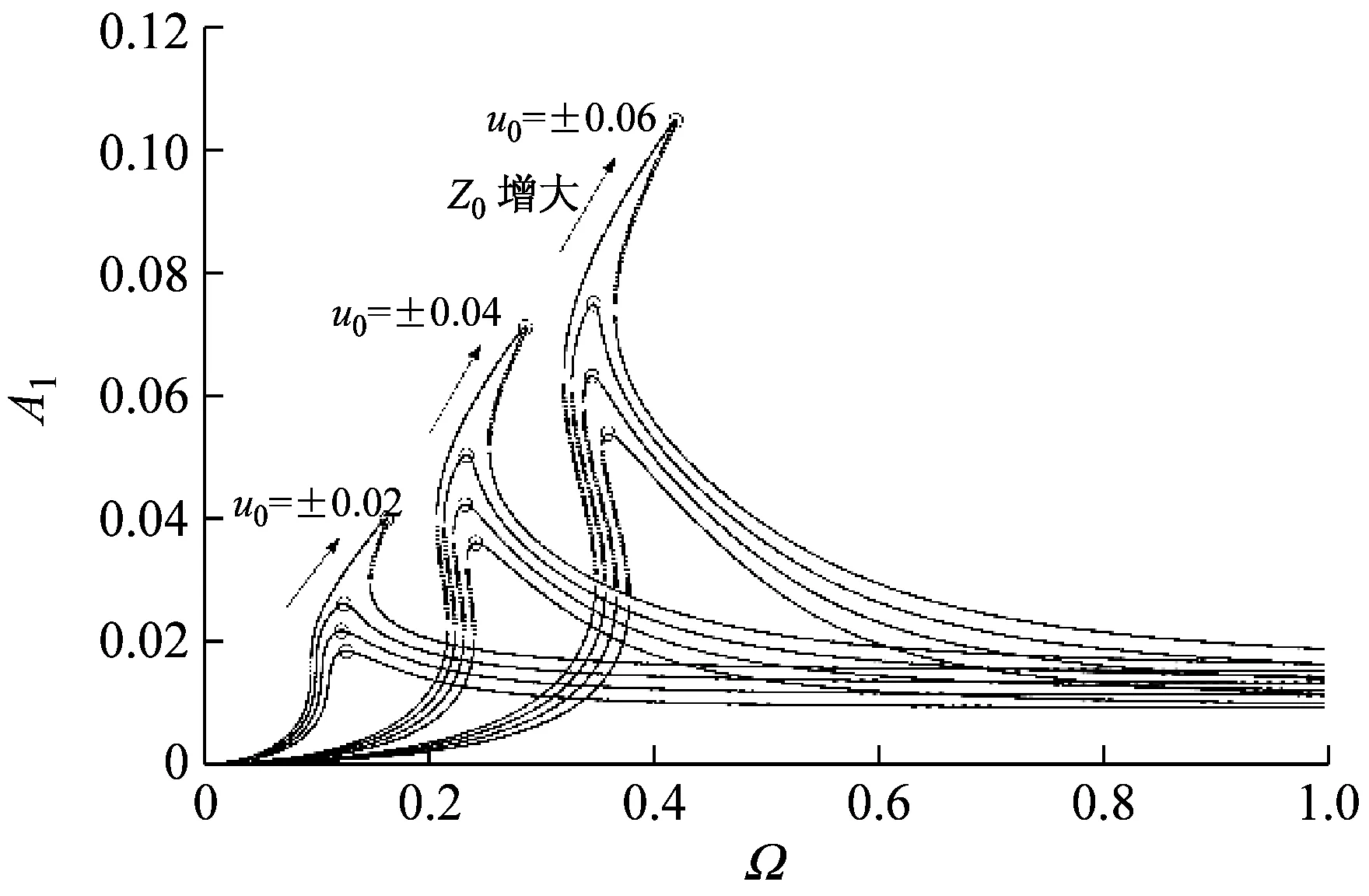
(a) 幅频响应曲线

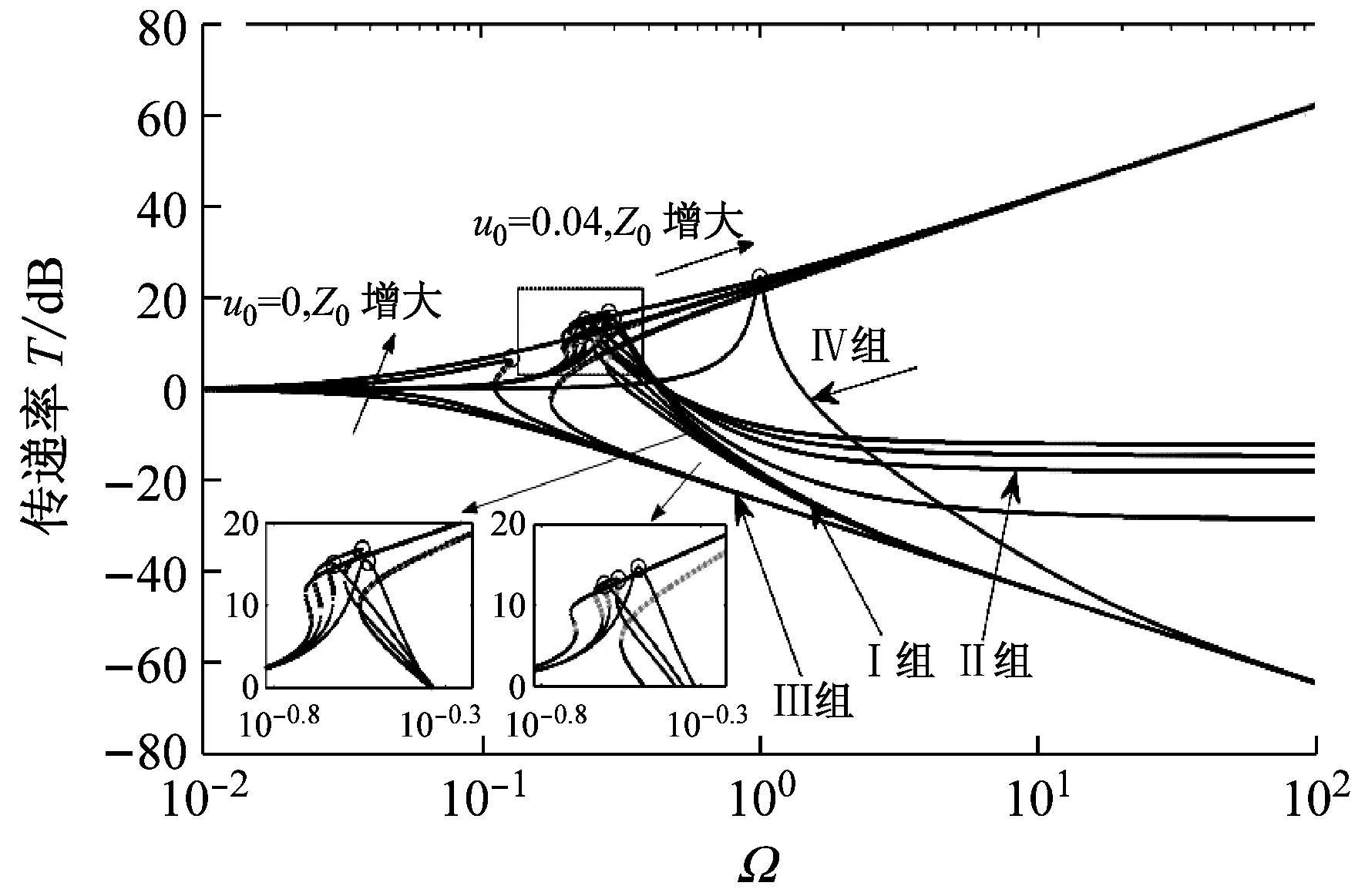
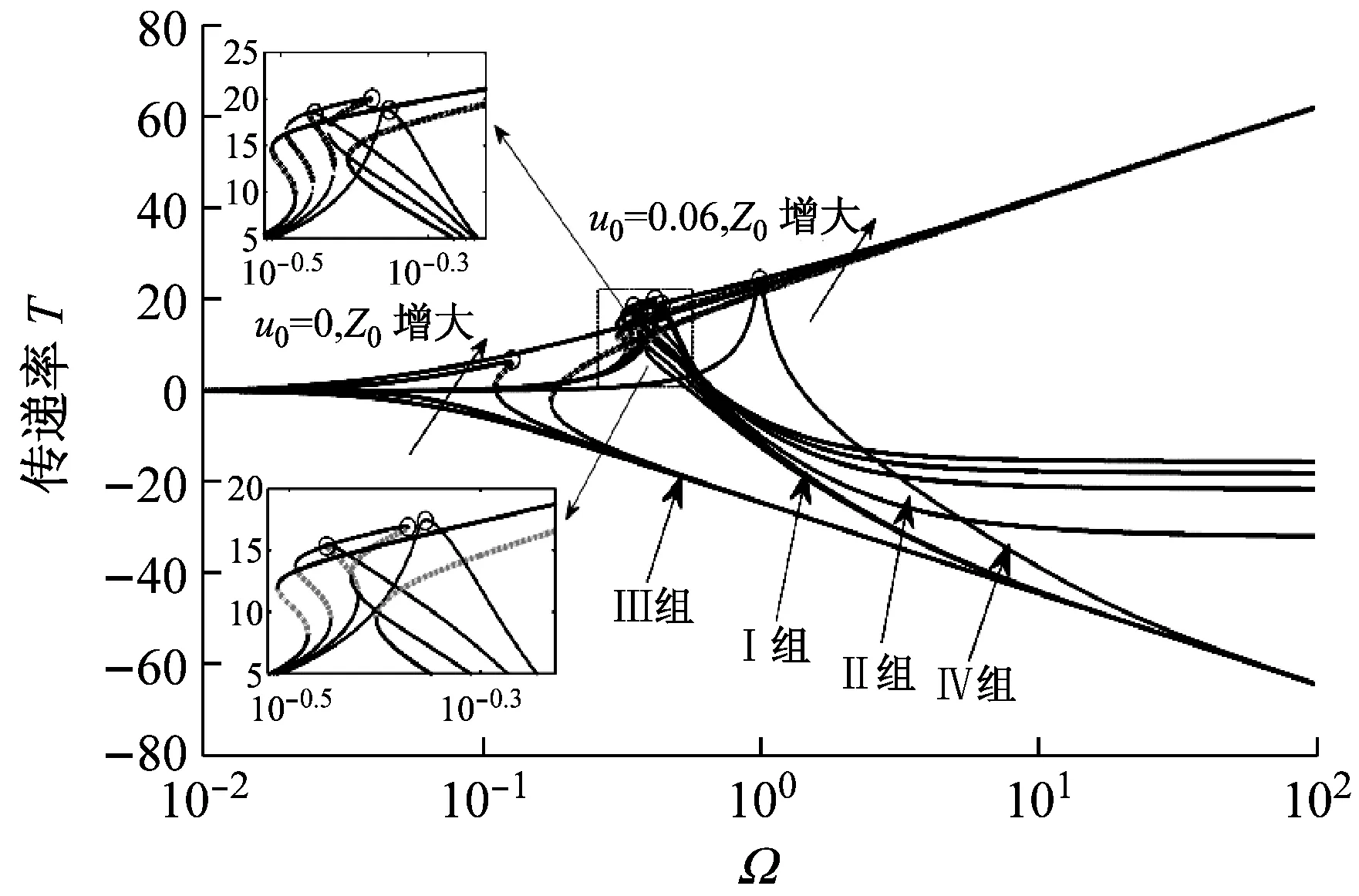
(b) 传递率曲线

(“I组曲线”—绝对加速度传递率，“II组曲线”—绝对位移传递率，“III组曲线”—理想系统传递率，“IV组曲线”—等效线性系统传递率，“虚线”—不稳定解)

图3 不同偏移量与激励幅值条件下的幅频响应与传递率曲线

Fig.3 FRCs and Transmissibility Curves of different offset displacements and excitation amplitudes

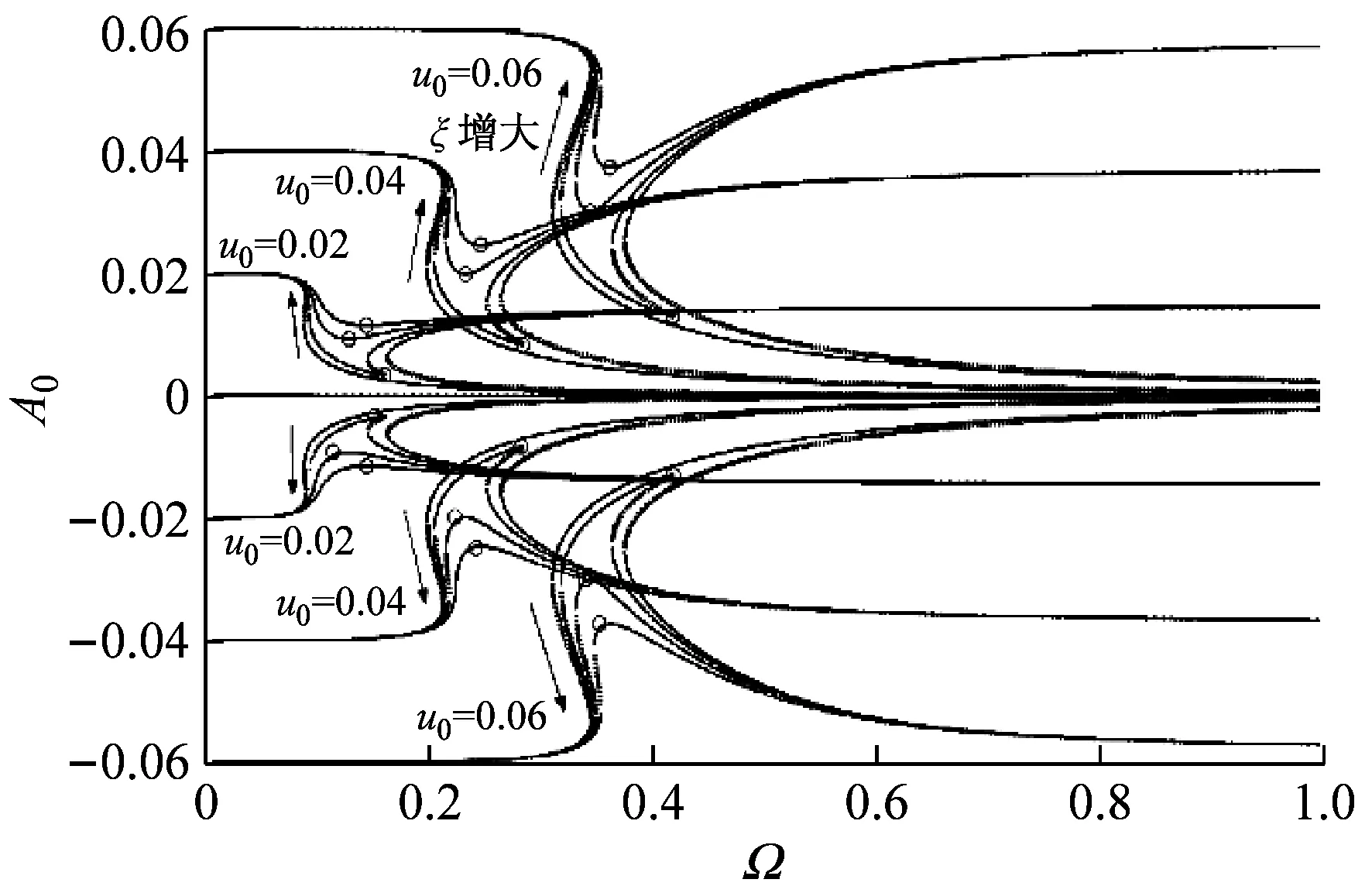
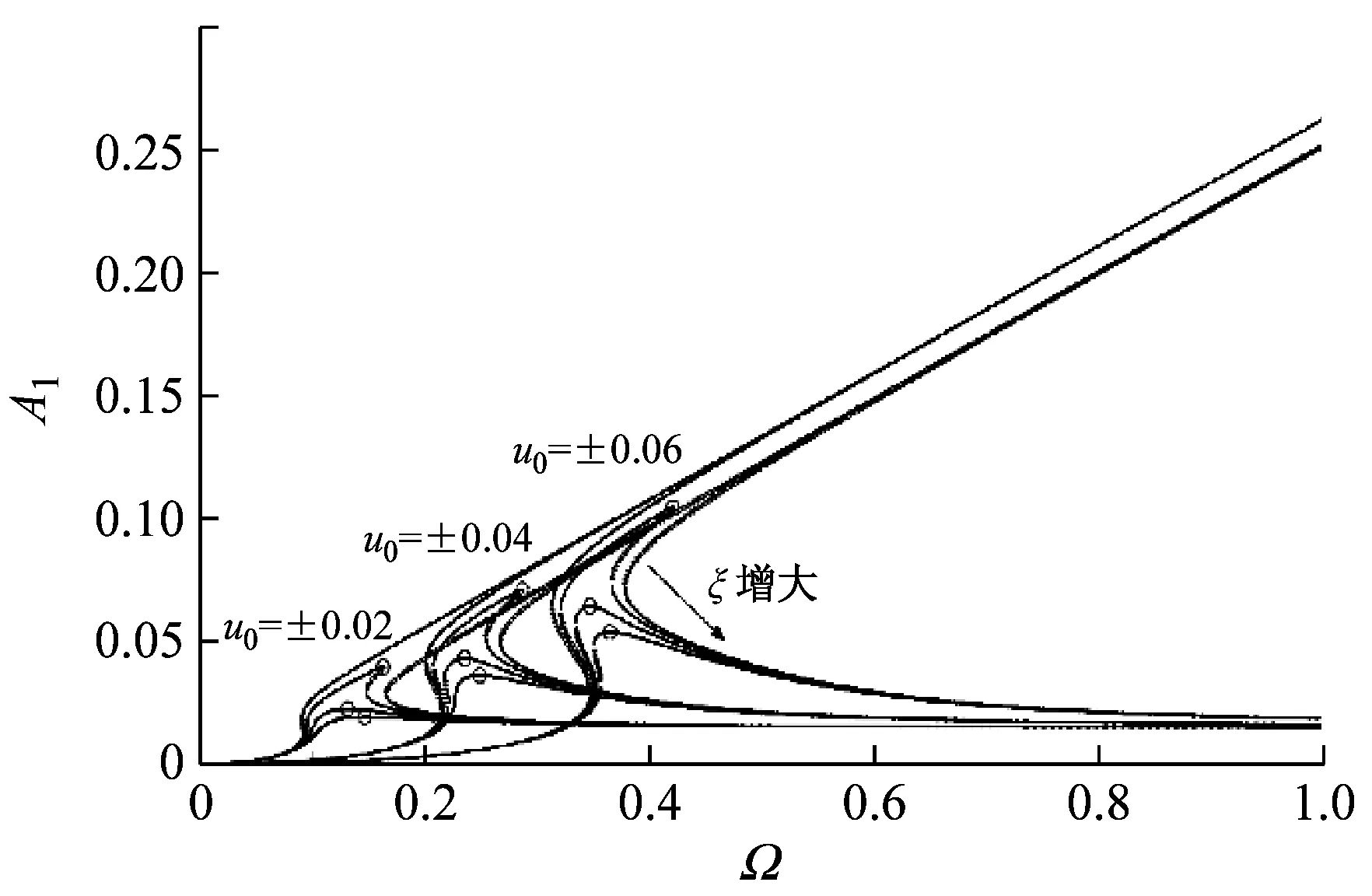
(a) 幅频响应曲线

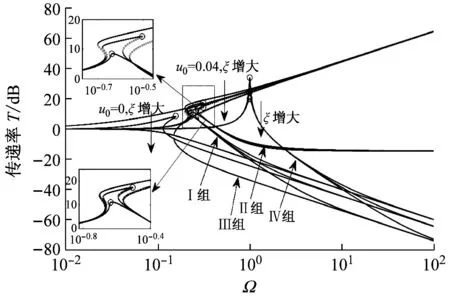
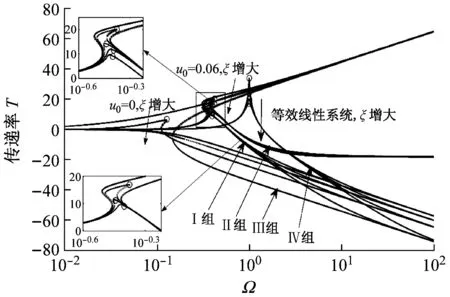
(b) 传递率曲线

(“I组曲线”—绝对加速度传递率，“II组曲线”—绝对位移传递率，“III组曲线”—理想系统传递率，“IV组曲线”—等效线性系统传递率，“虚线”—不稳定解)

图4 不同偏移量与阻尼比条件下的幅频响应与传递率曲线

Fig.4 FRCs and Transmissibility Curves of different offsetdisplacements and damping ratio

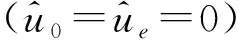
2.4 最小刚度为正值时的特性分析

当系统最小刚度为正值，即前文所建立的隔振器动力学模型中k1>0，依据式(13)、(17)(18)可分别研究系统频响特性与传递率特性，激励幅值、偏移量等具体参数设置见表2。

表2 谐波位移激励条件下的参数取值

如图5所示，为不同偏移量及线性刚度系数下的系统频响曲线，图中给出了最小刚度为零系统与等效线性系统的频响曲线作为比较。

如图5(a)，过载系统在给定的较小激励幅值下，未出现跳跃现象。系统响应的谐波项峰值随线性刚度系数变大而增大，系统响应常数项则随线性刚度系数变大而减小。随着线性刚度系数增大，过载系统最小刚度从零逐渐增大，其共振频率先减小后增大，系统响应的谐波项幅值逐渐增大，而常数项幅值峰值逐渐减小，即系统响应距离原平衡点的静态偏移量越小。换句话说，当非线性隔振器具有一定的线性刚度系数时，过载系统却可能具有更低的共振频率。

如图5(b)，具有较大偏移量的过载系统同样具有如图5(a)的频响特性。区别在于，随着线性刚度系数增大，共振频率低于零刚度过载系统的系统数量增多，也就是说在较小激励幅值条件下，对于较大偏移量的系统来说，随线性刚度增大过载系统共振频率先减小后增大的现象更明显。

由图5(c)可以看出，激励幅值增大，系统非线性明显增强，出现跳跃现象。随着线性刚度系数增大，系统共振频率先减小后增大，系统表现为渐软-渐硬及渐硬刚度特性。与较小激励幅值的情况相比，具有较大的正刚度且其共振频率低于最小刚度为零过载系统的系统数量呈减少趋势。

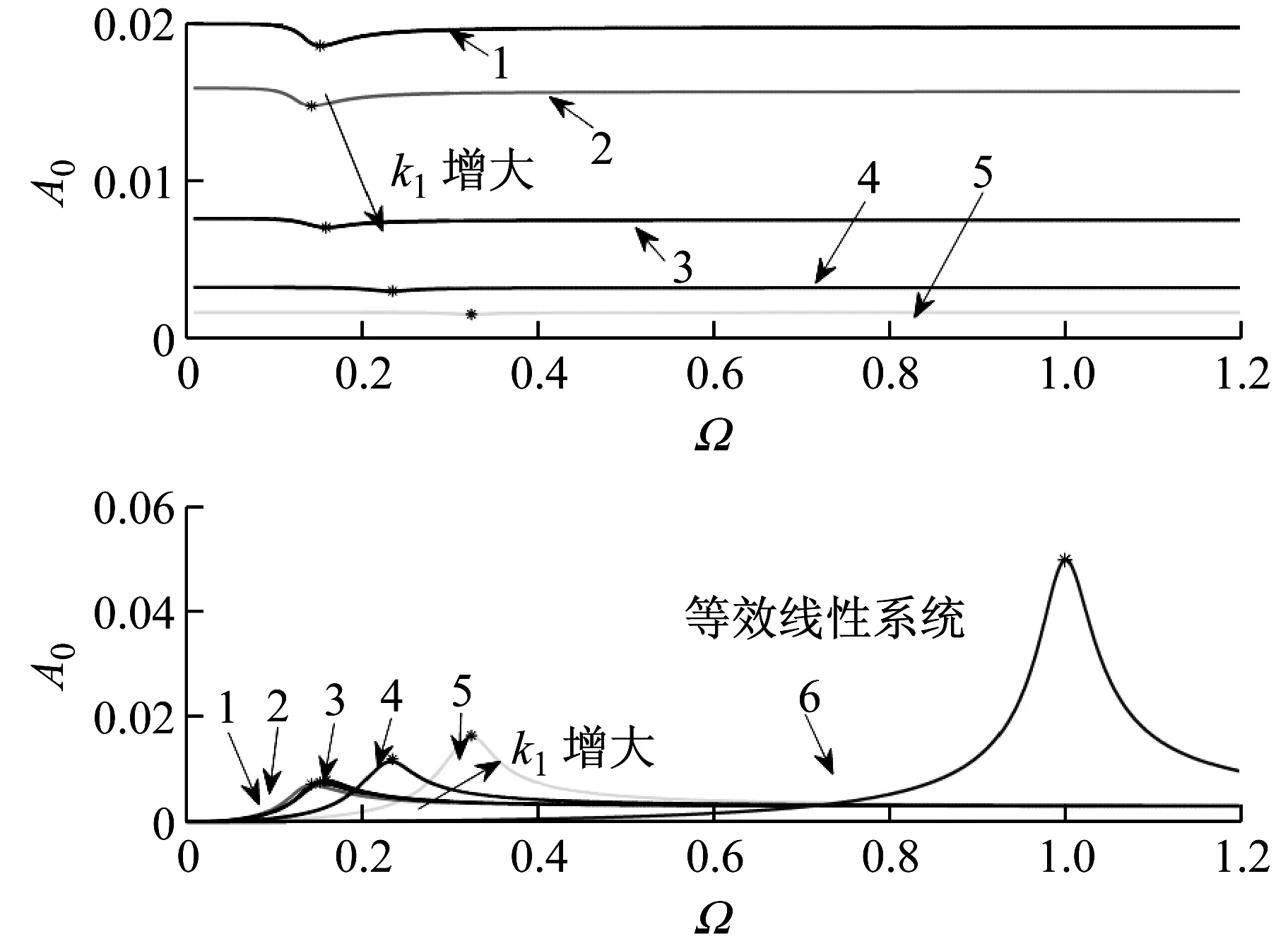
(a) 较小激励幅值较小偏移量的情况

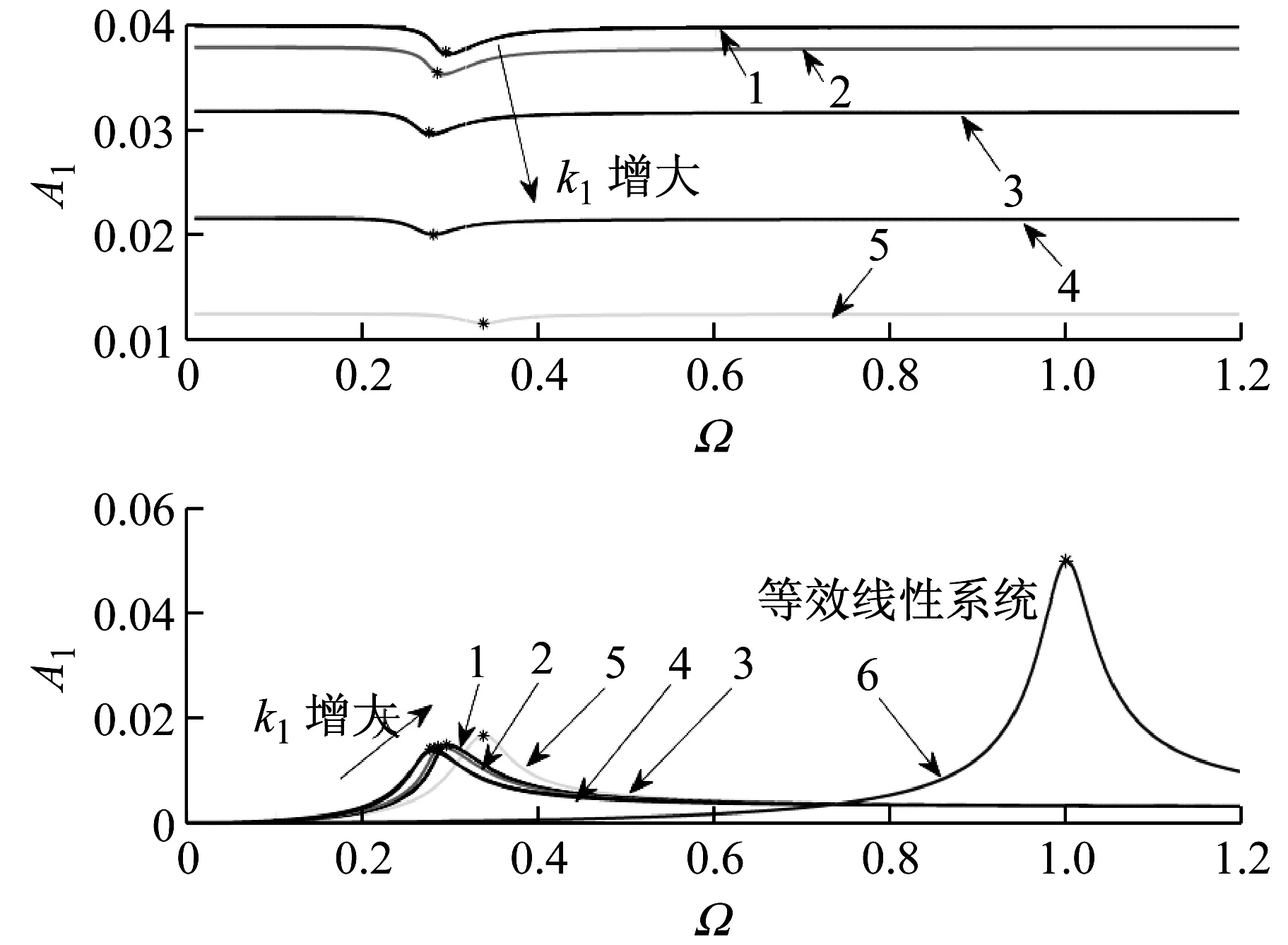
(b) 较小激励幅值较大偏移量的情况

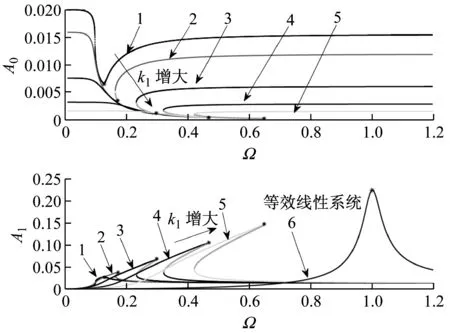
(c) 较大激励幅值情况

(“1”：k1=0，“2”：k1=0.005， “3”：k1=0.02，“4”：k1=0.05，“5”：k1=0.1，“6”—线性系统)

图5 不同偏移量与激励幅值条件下的系统频响曲线

Fig.5 FRCs of different offset displacements and damping ratio

由以上分析可以看出，对于较小激励幅值作用下的过载系统来说，若希望获得更低的共振频率，令系统拥有一个相对较小的正刚度比单纯追求低刚度更行之有效。这是由于一旦存在过载，系统响应中必然存在常数项，它会使系统响应的振动中心偏离静平衡位置一定距离，刚度越低，这种偏离越严重。

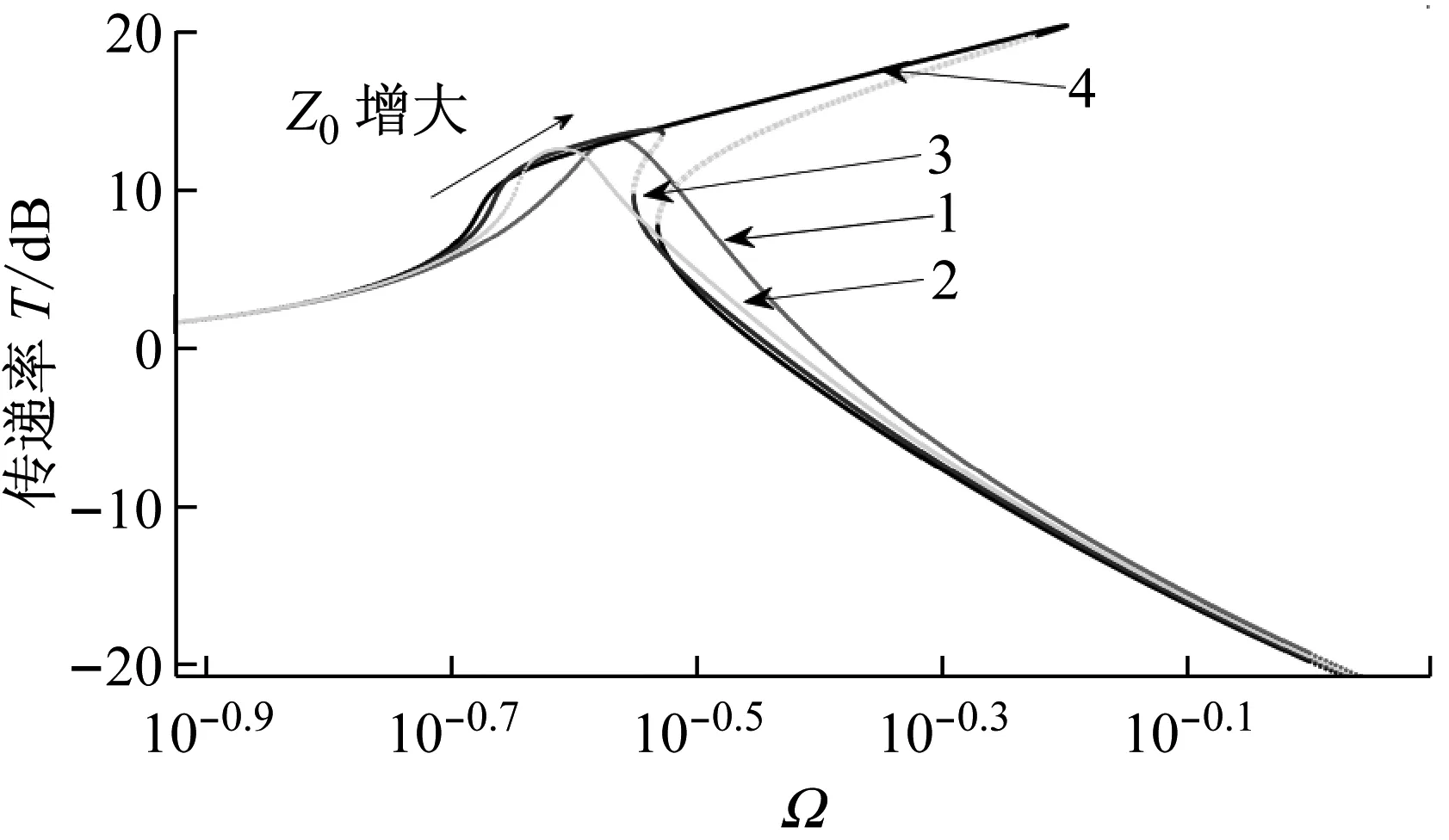
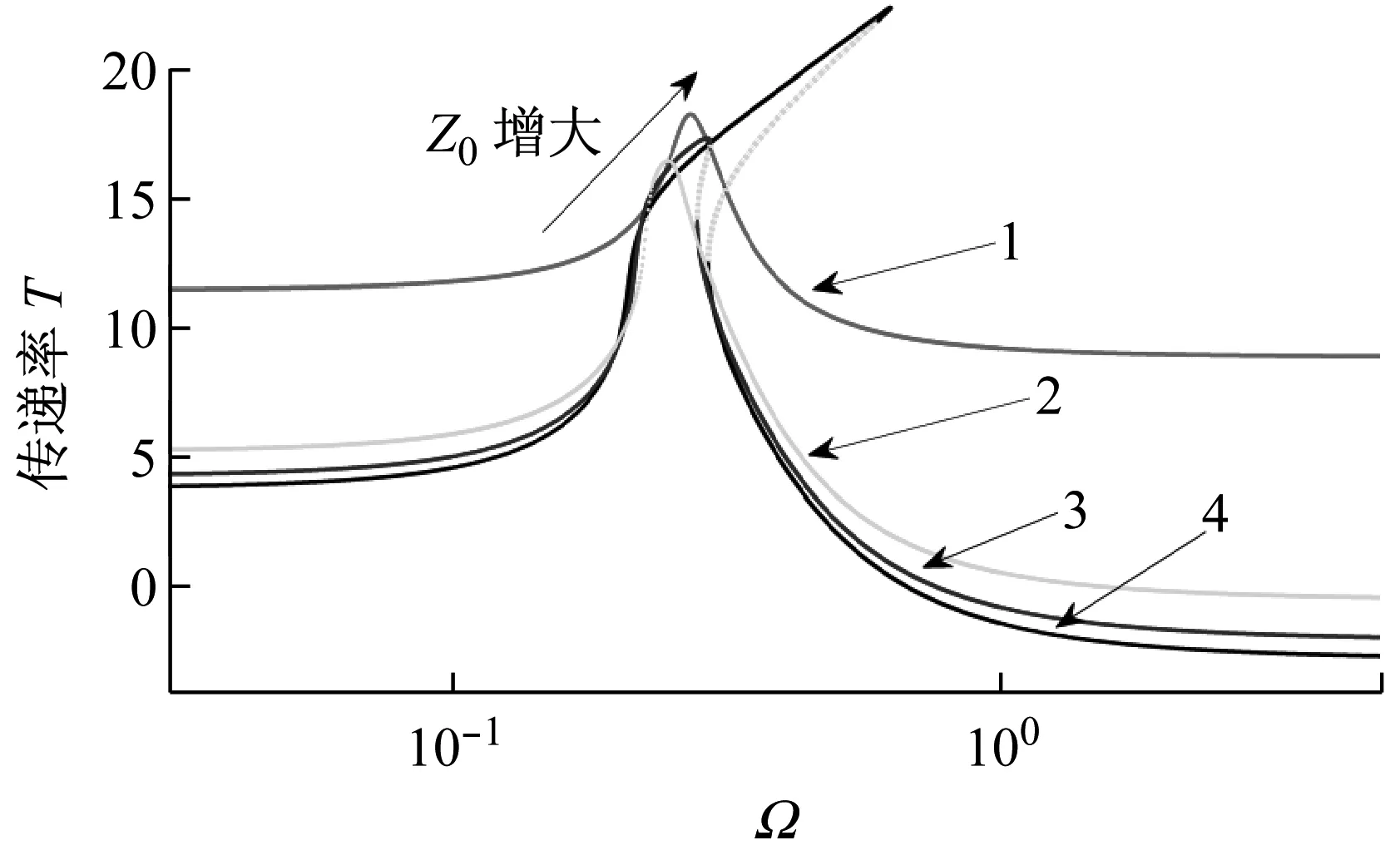
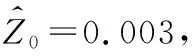
图6 不同激励幅值下的过载系统绝对加速度与位移传递率曲线

Fig.6 Absolute acceleration and displacement transmissibility curves of different excitation amplitudes

3 试验验证

为了验证理论分析的正确性，构建了该曲面-弹簧-滚子机构的非线性隔振器原理样机及振动试验平台，并开展了隔振器振动试验研究，如图8所示。

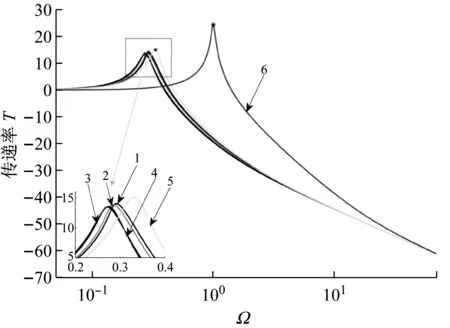
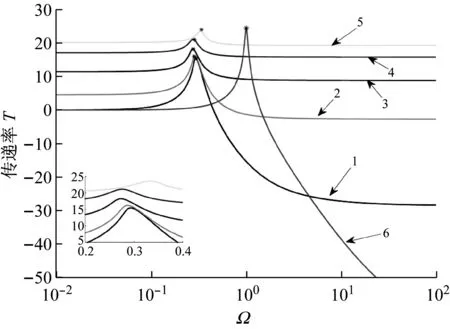
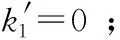
图7 不同线性刚度系数下的系统绝对加速度与位移传递率曲线

Fig.7 Absolute acceleration and displacement transmissibilitycurves of different linear coefficients

1.信号发生控制器；2.DASP信号采集系统；3.非线性隔振系统;4.液压振动台;5.计算机,6.响应加速度传感器;7.被隔振物体;8.隔振器;9.固定夹具;10.激励加速度传感器

图8 振动试验平台现场

Fig.8 Experimental setup

利用液压振动台，搭建了振动实验平台，并开展了优化前后隔振器隔振性能和过载条件下隔振器隔振性能测试试验，如图8所示。系统受到来自液压振动台的正弦位移激励，激励频率0.2～15 Hz，设定不同激励幅值分别为3、3.5、4、4.5、5 mm，超载质量为2 kg和4 kg。分别在液压振动台与被隔振物体表面布置加速度传感器，通过DASP数据采集分析软件采集两者在不同频率位移激励下的振动响应，分别得到隔振系统响应与位移激励的均方根值，二者之比即为隔振系统传递率。

系统受到来自液压振动台的正弦位移激励，激励频率为0.2～15 Hz，设定不同激励幅值分别为3、3.5、4、4.5、5 mm，超载质量为2 kg和4 kg。分别在液压振动台与被隔振物体表面布置加速度传感器，通过DASP数据采集分析软件采集两者在不同频率位移激励下的振动响应，分别得到隔振系统响应与位移激励的均方根值，二者之比即为隔振系统传递率。不同激励幅值条件下，过载系统的实际加速度传递率曲线，如图9所示。可以看出，随激励幅值增大，过载系统的传递率峰值及与之相对应的共振频率呈现先增大后减小的变化规律，与前文理论仿真分析的结果一致。但由于系统阻尼较大，试验并未出现非线性现象，这也印证了增大阻尼可使系统跳跃现象消失，避开不稳定区域的分析结论。图10所示为在3 mm激励幅值的谐波位移激励下，不同超载质量系统的传递率对比图。可以看出，随着超载质量增大，系统偏移量增大，隔振系统传递率曲线峰值和响应的共振频率均增大，但隔振性能依然优于线性系统。

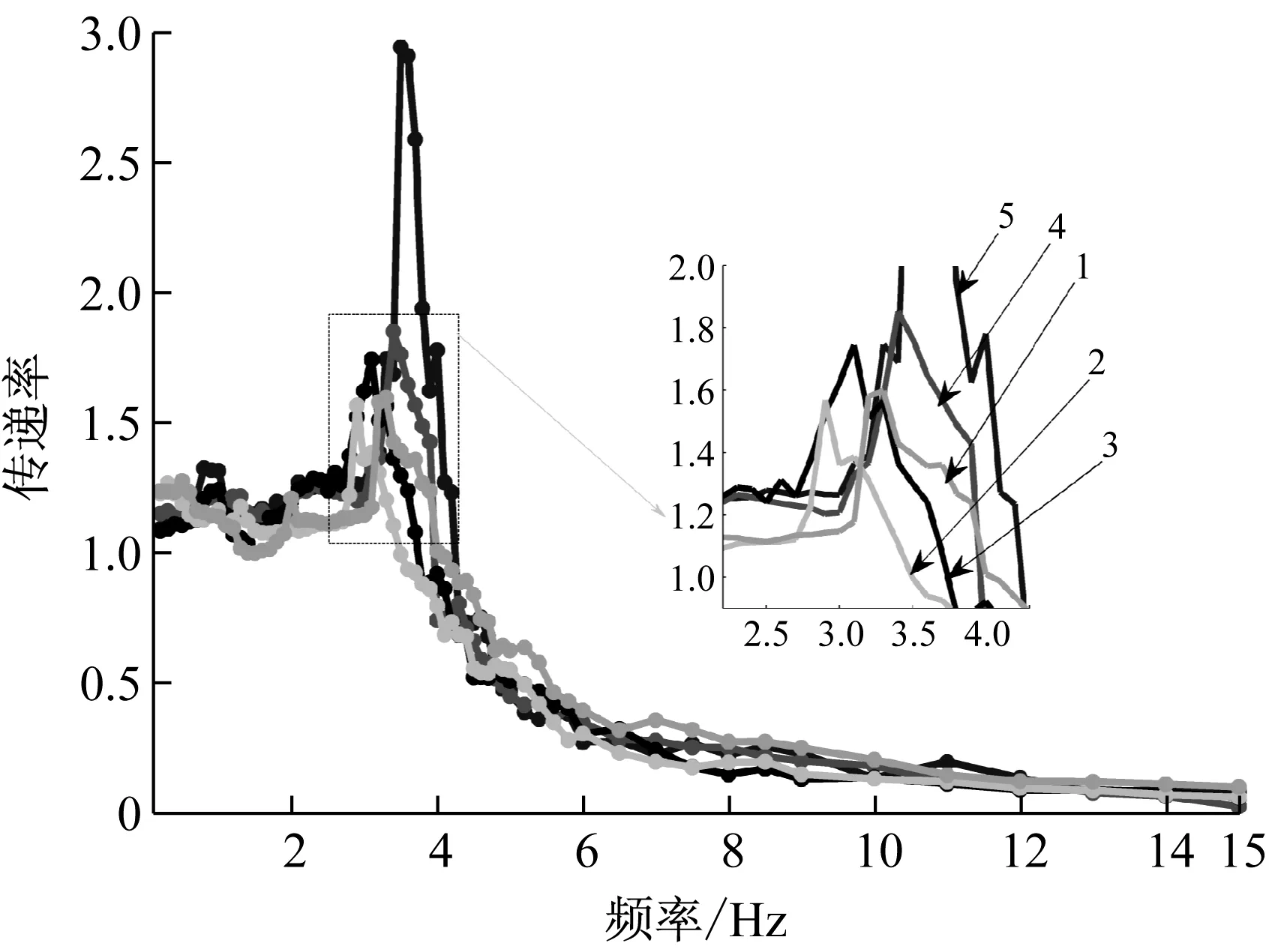
(“1”-3 mm； “2”-3.5 mm； “3”-4 mm； “4”-4.5 mm； “5”-5 mm)

4 结 论

本文采用曲面、弹簧、滚子构成的负刚度机构设计了一种非线性隔振器，得到了隔振器具有零刚度的参数条件，建立了过载系统的非线性动力学方程，定义了绝对位移传递率与绝对加速度传递率；分别研究了隔振器最小刚度为零和为正值时，过载系统的动态特性。结果表明，最小刚度为零的过载系统，在谐波位移激励下，随激励幅值增大呈现渐软或渐软-渐硬、渐硬及无限大响应渐硬的刚度特性；随偏移量减小，系统稳态响应解常数项幅值、谐波项幅值及相应的共振频率均越小，系统隔振频率范围扩大，且最低隔振起始频率降低，但始终大于偏移量为零时的值；适当的减小偏移量和激励幅值大小，可提高系统隔振性能，增大阻尼比，可减小系统响应幅值峰值，避免过载系统可能存在的跳跃现象与不稳定区域，但却以牺牲高频区域内隔振性能为代价而提高其低频隔振性能。最小刚度为正值时，当激励幅值较小且系统偏移量较小时，随最小刚度由小到大，过载系统响应的谐波项峰值增大而常数项峰值减小，共振频率先减小后增大，出现共振频率最小的系统为具有一定正刚度系统的现象；当激励幅值较小且系统偏移量增大，随最小刚度由小到大，共振频率最小的系统所对应的正刚度增大；当系统偏移量较小而激励幅值增大时，随系统最小刚度增大，共振频率最小的系统所对应的正刚度值减小。故，对于受较小激励的过载系统而言，若希望获得较小的共振频率，可使系统具有一定正刚度。

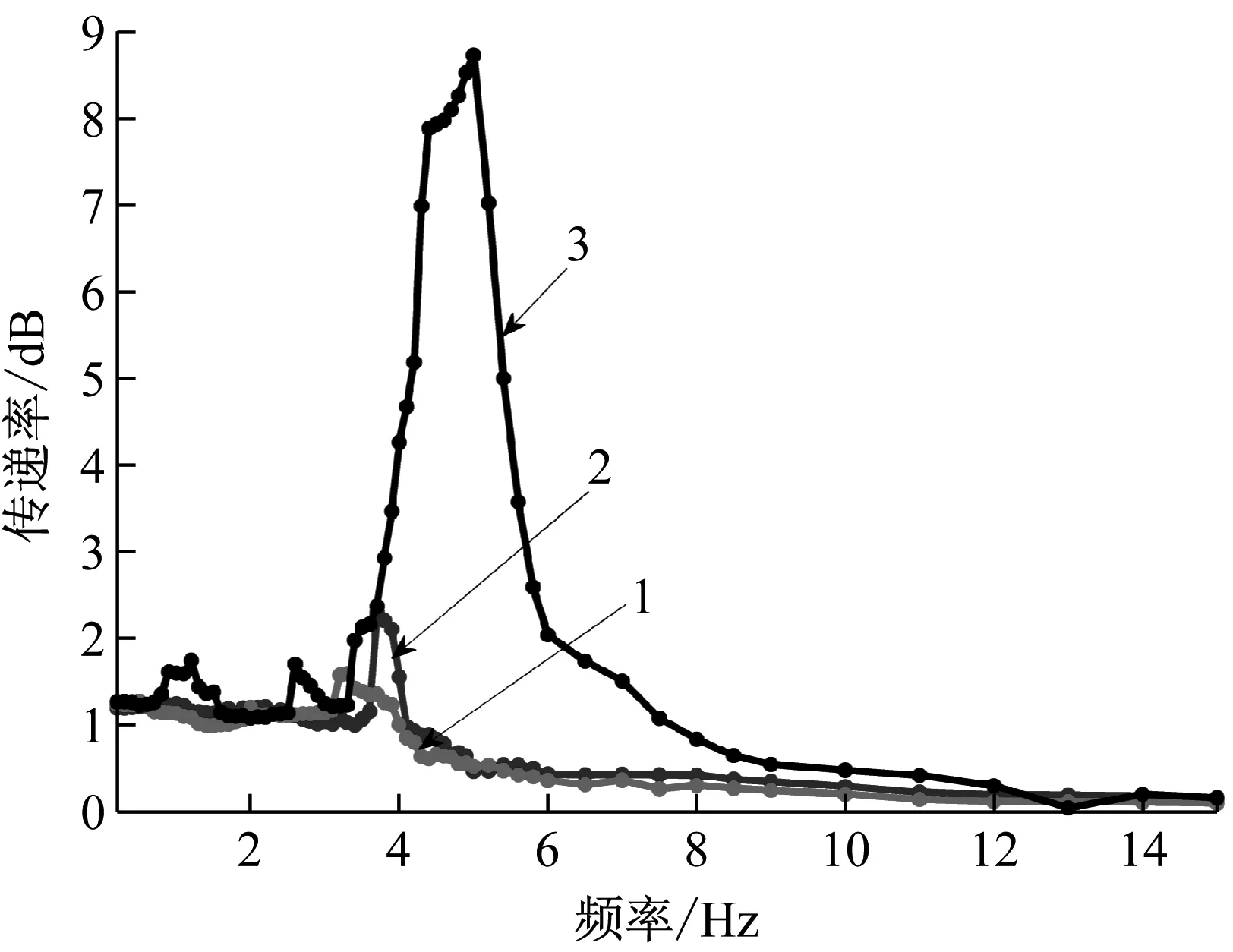
(“1”—2 kg， “2”—4 kg， “3”—线性系统)

通过实验研究验证了最小刚度为零条件下过载系统的隔振特性。结果表明，随着激励幅值增大，过载系统传递率峰值及与之相应的共振频率先减小后增大；随着偏移量减小，系统传递率曲线峰值和响应共振频率减小；当阻尼比过大时，实际传递率曲线并未出现非线性现象，阻尼比增大有助于消除系统跳跃现象和不稳定区域。与线性隔振器相比，即使是过载或欠载使用，具有负刚度机构的隔振器仍然具有很好的低频隔振性能，因此负刚度机构是一种非常有效的减小共振频率的方法。

在该类非线性隔振器的设计与使用中，选择设置合理的刚度系数、阻尼系数，并适当限制其所能承受的最大激励幅值，以保证系统具有较低的共振频率并避免出现响应幅值过大，使隔振器具有较好的隔振性能。本文为该类隔振器的实现提供了一套非常有用的设计方法，能够今后该类非线性隔振器的设计提供很好的参考与借鉴。