一类内共振非线性随机振动系统的可靠性控制

齐玉明， 吴勇军

(上海交通大学 工程力学系，上海 200240)

结构或机械系统常常受到随机激励的作用。为获得系统的统计信息，一个简单易行的办法是采用数值模拟，但数值模拟需要耗费大量计算时间。另一方法是基于合理数学模型的理论分析法。目前，最成熟的理论方法是基于扩散的Markov过程理论[1]。为应用该理论，随机激励常常需模型化为高斯白噪声。经添加Wong-Zakai修正项，系统的运动微分方程可用It随机微分方程表示。系统的动态可靠性函数、瞬态(稳态)响应概率密度等可通过求解相应的后向Kolmogorov方程或Fokker-Planck-Kolmogorov(FPK)方程得到。由于实际系统通常是多自由度系统，相应地，这两个方程常常为高维偏微分方程，数学上求解很困难，一般只能数值求解[2]。

研究中常常需要对系统施加反馈控制，以达到一定的设计目的。对于一个随机系统，研究得最多、理论上最成熟的是扩散Markov过程的随机最优控制问题，其控制的目的是使系统的某项指标达到最优。求解随机最优控制问题的两个主要方法是Pontryagin极大值原理与Bellman的动态规划[3]。关于动态规划方法已有很多的研究成果。应用该方法的主要困难在于求解高维非线性的Hamilton-Jacobi-Bellman(HJB)方程,大多数情况下，只能得到数值解，无法获得精确解析解[4-5]。

可见，无论是对随机动力学还是随机最优控制问题的研究，经常会碰到高维问题。为简化问题的数学处理，一个有效的方法是模型降阶(Model Reduction)。模型降阶是一个重要的问题，在结构动力学、计算数学、系统与控制中都会碰到[6]。在随机动力学中，随机平均法是一种强有力的降阶方法。迄今，已发展了多类随机系统的随机平均法。由于具有诸多优点，随机平均法已被广泛用于系统的响应预测、可靠性估计以及稳定性分析等[7]。自然地，将随机平均法与动态规划原理结合，将为随机最优控制问题的研究带来极大的便利。近20年中，朱位秋等将随机激励的拟哈密顿系统随机平均法与动态规划原理结合，提出了以响应最小、可靠度最大、稳定度最大为目标的多自由度拟哈密顿系统随机最优控制方法。朱位秋等通过数值模拟及工程实例，验证了该方法的有效性。

动态可靠性问题是随机动力学中的一个重要问题，与系统的状态迁移和使用寿命密切相关。为提高系统可靠性，需要研究反馈控制。如前所述，在可靠性最优控制的理论分析中，将随机平均法与动态规划原理结合亦是一种有效的方法。近10年，已有的研究大多采用了该方法[8-10]。朱位秋等在高斯白噪声激励的拟哈密顿系统随机平均法的基础上，结合随机动态规划原理，给出了高斯白噪声激励下拟不可积、无内共振拟可积、无内共振拟部分可积三类拟哈密顿系统可靠性最优控制问题的一般性数学提法。应该指出的是，在应用随机平均法研究多自由度随机振动系统可靠性的最优控制时，需要区分系统是否存在内共振。已有的研究中，为简化问题的数学处理，没有考虑存在内共振的情况。

本文将无内共振情况加以推广，研究了一类拟可积哈密顿系统在有内共振情况下首次穿越可靠性的最优控制。随机激励模型化为高斯白噪声。利用广义谐和函数随机平均法，受控系统的运动方程简化为部分平均的It随机微分方程。基于动态规划原理，建立了以可靠度最大为目标的动态规划方程，求得了最优控制力。进一步，得到了最优控制系统的It随机微分方程，分别建立了控制系统的条件可靠性函数与平均首次穿越时间满足的后向Kolmogorov方程及Pontryagin方程，给出了边界条件及初始条件。在具体算例中，得到了受控及未控系统的条件可靠性函数和平均首次穿越时间，用Monte Carlo数值模拟验证了理论方法的有效性。

1 内共振系统的部分平均It随机微分方程

考虑如下受弱高斯白噪声及弱反馈控制作用的n自由度拟哈密顿系统：

εui(Q,P),

i,j=1,2,…，n;k=1,2,…，m

(1)

此处，Q=[Q1,Q2, …,Qn]T,P=[P1,P2, …,Pn]T,Qi、Pi分别为广义位移和广义动量；H是哈密顿函数；cij(Q，P)表示阻尼系数；Zk(t)是平稳高斯白噪声，自相关函数为Rkl(τ)=E[Zk(t)Zl(t+τ)]=2Dkl×δ(τ)；hik(Q，P)表示随机激励的幅值；ui(Q，P)表示反馈控制力；ε是小参数。重复下标表示求和。

注意到保守的哈密顿系统可以是可积、不可积的。假设(1)中的哈密顿函数H经正则变换是可分离的，即

(2)

大多数情况下，H表示系统总能量，Hi代表各子系统能量，可表示为

(3)

Ui表示势能，定义dUi/dQi=gi(Qi)。由此，系统(1)表示一类受控的拟可积哈密顿系统，可进一步改写为

εui(Q,P),

i,j=1,2,…n;k=1,2,…m

(4)

将系统(4)的解表示为如下的广义谐和函数形式[11]：

Qi(t)=AicosΦi(t)+Bi,

Pi(t)=-Aiνi(Ai,Φi)sinΦi(t)

(5)

此处，

Φi(t)=τi(t)+Θi(t),

(6)

式中：Ai、τi、Θi、Φi、νi及Bi均为随机过程，式(6)中，Ai、νi分别为第i个子系统的振幅和瞬时频率。Bi可通过如下关系式确定[3]：

Ui(Ai+Bi)=Ui(-Ai+Bi)=Hi

(7)

平均频率ωi(Ai)可由如下关系得到

(8)

可有如下的近似关系：

Φi(t)≈ωi(Ai)t+Θi

(9)

结合式(4)～(5)，可得如下的随机微分方程：

i=1,2,…,n;k=1, 2,…,m

(10)

此处，

A=[A1,A2,…An]T,Φ=[Φ1,Φ2,…Φn]T,u=[u1,u2,…un]T,

(11)

方程(10)是Stratonovich意义下的随机微分方程。添加Wong-Zakai修正项，得如下It随机微分方程：

(12)

Be(t)为独立维纳过程。漂移与扩散系数为：

i,i1,j1=1,2,…n;p=1,2;

k,s=1,2…m;e=1,2…m

(13)

考虑系统(4)存在内共振的情况，此时，各子系统的平均频率ωi(Ai)之间存在如下(个 (1≤η≤n-1)关系：

Nsjωj=εσs,s=1,2,…,η;j=1,2,…,n

(14)

这里的Nsj为整数，σs为小参数。

引入η个 (1≤η≤n-1)新变量：

Γs=NsjΦj,

s=1,2,…η;j=1,2,…n

(15)

i,j=1,2,…,n;z=η+1,…,n;

s=1,2,…,η;e=1,2,…,m

(16)

方程(16)中，Γ=[Γ1,Γ2, …,Γη]T，Φ′=[Φη+1, …,Φn]T。利用式(15)，[Φ1,…,Φη]T可用[Γ1,Γ2, …,Γη]T表示。

由(16)可以看到，随机过程[A,Γ]T为慢变过程，而Φ′为快变过程。对快变过程做平均，得到如下平均It随机微分方程：

i=1,2,…,n;s=1,2,…,η

(17)

平均后的漂移与扩散系数为：

i,j=1,2,…,n;s1,s2=1,2,…,η

(18)

由于控制力u未知，方程(17)中只得到部分平均的漂移系数。

2 动态规划方程与最优控制律

从式(5)可以看到，随机过程A表示振幅，在[0,+∞)随机变化。可认为Ai超过某个阈值Aic，系统即发生首次穿越损坏。施加控制的目的是减小系统发生损坏的概率，以使系统的可靠性最大，或平均首次穿越时间最长。定义如下的值函数：

τp∈(t,tf]Α(t,u)∈Ωs}

(19)

Ωs为系统的安全域，u∈U表示控制约束，tf是控制终了时刻。式(19)表示V(t,A)是最优控制系统的可靠性函数。根据Zhu的专著，V(t,A)满足如下的动态规划方程：

0≤t≤tf,Ai∈[0,Aic),i,j=1,2,…,n

(20)

类似地，对平均首次穿越时间最长的控制问题，定义如下的值函数：

(21)

τp(Α,u)表示首次穿越时间，E表示数学期望。V1满足如下的动态规划方程[3]：

(22)

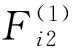
ui≤δi,i=1,2,…,n

(23)

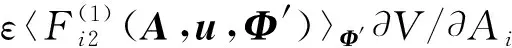
(24)

显然，可靠性函数是振幅Ai的递减函数[10]。因此∂V/∂Ai<0。注意到gi(Ai+Bi)和(1+ρi)通常都为正。(24)进一步简化为：

(25)

将式(25)的最优控制力代入方程式(17)，完成平均，得到如下完全平均It随机微分方程：

i=1,2,…,n;s=1,2,…,η

(26)

完整的漂移系数为：

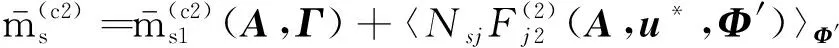
(27)

3 最优控制系统的条件可靠性函数与平均首次穿越时间

方程式(26)描述了最优控制系统的状态。最优控制系统的条件可靠性函数Rc(t|A0,Γ0)为初始状态[A0,Γ0]T及时间t的函数，其数学定义为：

Rc(t|Α0,Γ0)=Probability{[Α(τp),Γ(τp)]T∈Ωs,

τp∈[0,t] [Α0,Γ0]T∈Ωs}

(28)

根据扩散过程理论，Rc(tA0,Γ0)满足如下的后向Kolmogorov方程：

(29)

偏微分方程式(29)的边界和初始条件为：

Rc(0A0,Γ0)=1,Ai0∈[0,Aic),Γs0∈[0,2π],

Rc(tA0,Γ0)=0,Ai0=Aic,Γs0∈[0,2π],

Rc(t0,Γ0)=finite,Γs0∈[0,2π],

Rc(tA0,0)=Rc(tA0,2π)

(30)

首次穿越时间T的概率密度通过下式求得：

(31)

最优控制系统的平均首次穿越时间μc(A0,Γ0)是初始状态[A0,Γ0]T的函数，由如下的Pontryagin方程确定：

(32)

偏微分方程(32)满足如下的边界条件：

μc(A0,Γ0)=0,Ai0=Aic,Γs0∈[0,2π],

μc(0,Γ0)=finite,Γs0∈[0,2π],

μc(A0,0)=μc(A0, 2π)

(33)

方程式(29)与(32)是高维偏微分方程，通常只能通过数值方法求解，如有限差分法。

4 算 例

考虑如下受高斯白噪声及弱控制作用的二自由度Duffing-van der Pol系统。运动微分方程为：

(34)

Zij(t) (i,j=1, 2)为独立的平稳高斯白噪声，强度为2Dij。βi0,βij,ηij,ω0i,αi为常数。

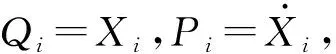
(35)

漂移与扩散系数的表达式见附录。

最优控制系统的条件可靠性函数满足如下的后向Kolmogorov方程：

(36)

初始与边界条件为：

Rc(0|A10,A20,Γ0)=1,Ai0∈[0,Aic),Γ0∈[0,2π],

Rc(t|A10,A20,Γ0)=0,Ai0=Aic,

Rc(t|A10,A20,0)=Rc(t|A10,A20,2π),

i=1,2

(37)

计算中选取如下参数：βi0=βij=0.01，ω01=2.03，ω02=2.14，αi=1.0，ηij=0.2，D11=D12=D22=0.03,D21=0.004,Aic=0.5。用显式格式的中心差分法求解偏微分方程式(33)，得到最优控制系统的条件可靠性函数。图1～2给出了一组结果。可以看到，理论结果与数值模拟比较吻合。无控制时(δi=0)，系统可靠性函数较小。增大控制力(δi=0.02, 0.03)，系统的可靠性函数得到提高。

最优控制系统的平均首次穿越时间Tc(A10,A20,Γ0)满足如下Pontryagin方程：

(38)

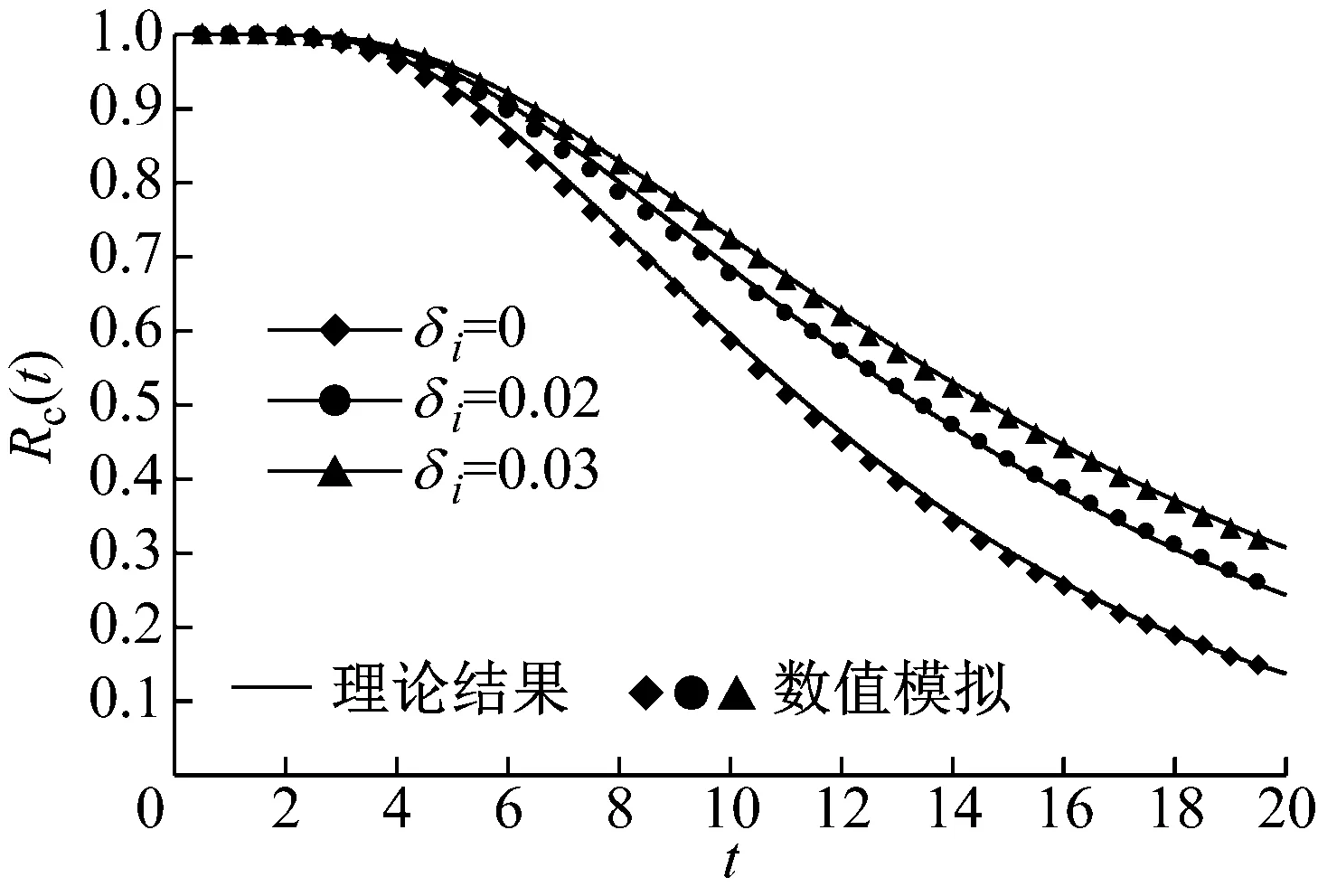
图1 系统(34)的最优控制条件可靠性函数

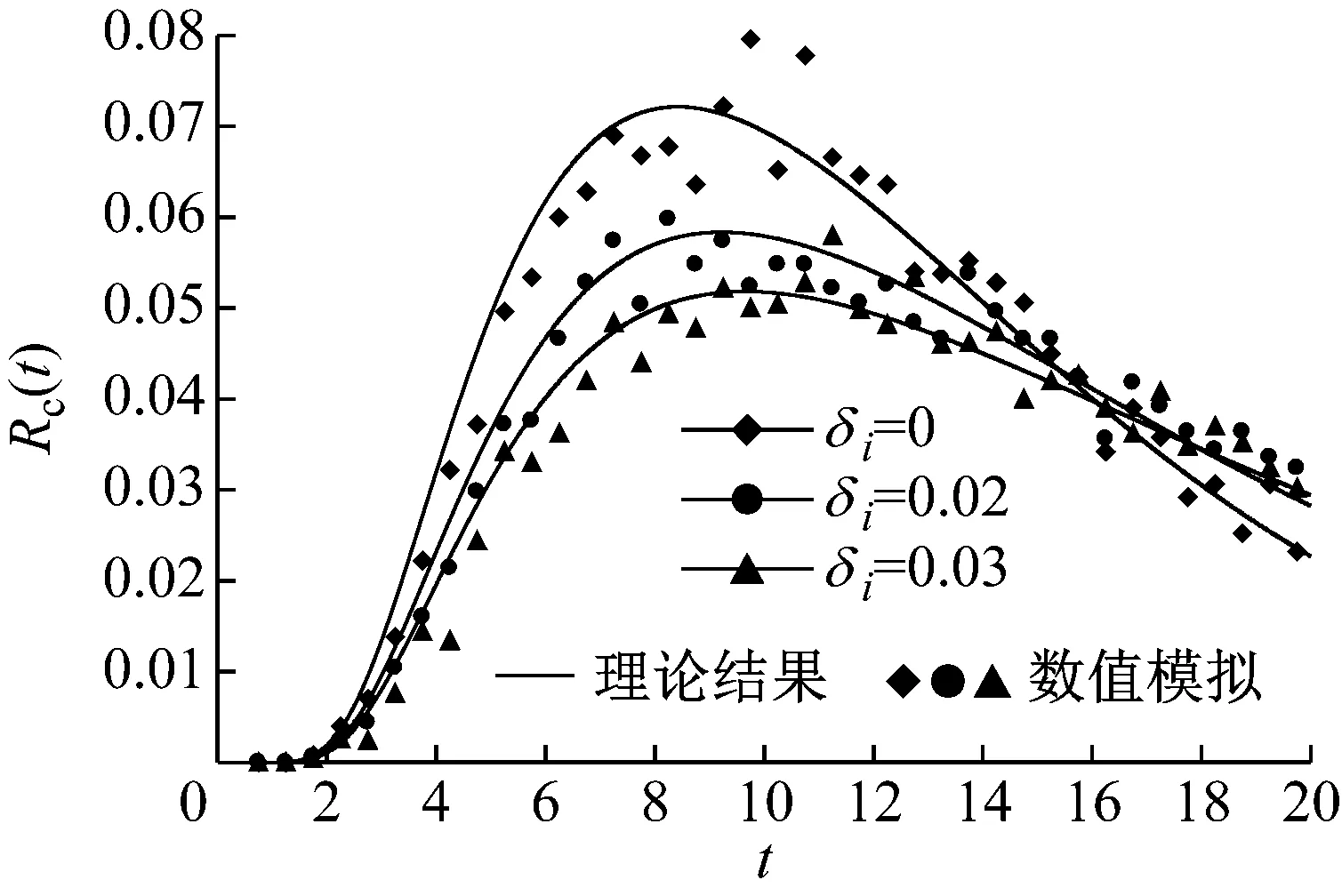
图2 系统(34)的最优控制首次穿越时间概率密度

边界条件为：

Tc(A10,A20,Γ0)=0,Ai0=Aic,

Tc(A10,A20,0)=Tc(A10,A20,2π)，i=1,2

(39)

用中心差分法结合超松弛迭代法，求解偏微分方程式(38)，得到最优控制系统的平均首次穿越时间。图3给出了一组结果。可以看到，理论结果与数值模拟比较吻合。增大控制力，能提高系统的平均首次穿越时间，也即提高了系统的可靠性。

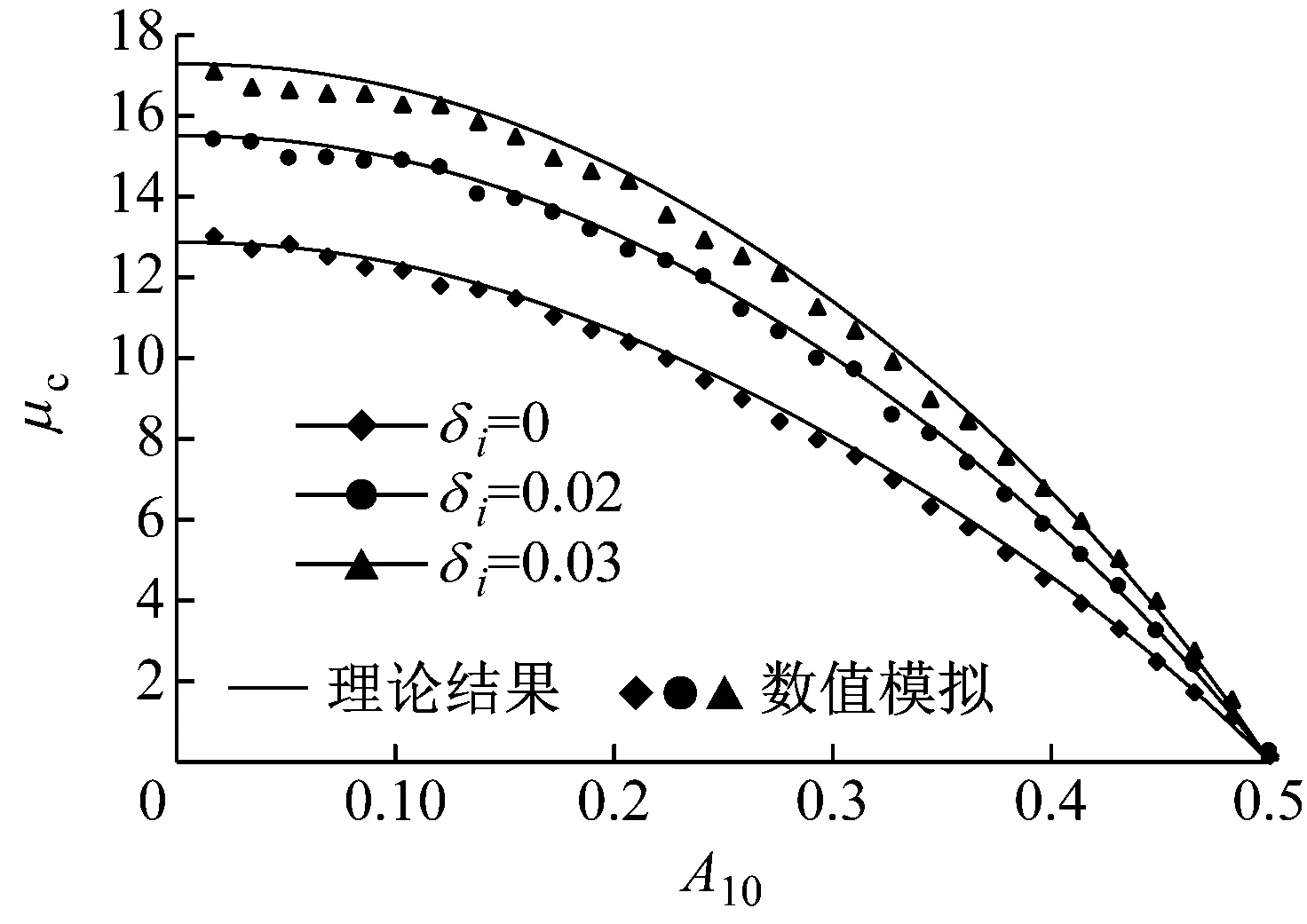
图3 系统(34)的最优控制平均首次穿越时间

5 结 论

本文研究了一类随机激励的多自由度非线性内共振拟可积哈密顿系统的首次穿越可靠性的最优控制问题，给出了该问题的一般性数学提法。首先基于随机平均法，得到了内共振情形部分平均的It随机微分方程。定义了以可靠度最大及平均首次穿越时间最长为目标的值函数，根据动态规划原理，建立了动态规划方程，确定了最优控制力的形式，进而得到了完全平均的最优控制系统的It随机微分方程。在此基础上，建立了最优控制系统条件可靠性函数满足的后向Kolmogorov方程及平均首次穿越时间满足的Pontryagin方程。以二自由度Duffing-van der Pol系统为例，得到了内共振的最优控制系统的平均It随机微分方程，其漂移系数与扩散系数不同于无内共振系统。以及内共振情形最优控制系统的条件可靠性函数和平均首次穿越时间。结果表明，理论结果与Monte Carlo数值的结果较吻合，证明了理论方法的有效性。

显然，内共振的存在增加了数学处理的难度。在推导内共振系统的部分平均It随机微分方程时，除了振幅是慢变量外，还需要考虑由相位角定义的慢变量，由此得到的决定最优控制系统的平均It随机微分方程的维数更高。相应地，需要求解更高维数的偏微分方程，以得到最优控制系统的条件可靠性函数及平均首次穿越时间。另一方面，系统是否存在内共振与参数选取有关。由于实际系统的非线性特性，导致系统频率与系统的响应有关，这与线性系统不一样。一般情况下，由于系统的外加激励大小的多样性，系统的平均固有频率在一定的范围内变化，导致内共振常常无法避免。

注意到算例中，系统为二自由度振动系统。对于实际中的机械或结构系统，其自由度可能更高。本文的方法仍适用，只是需要求解更高维数的偏微分方程，需要更多的计算时间，数学处理更困难。

附录：It随机微分方程(35)的漂移与扩散系数

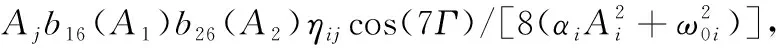
A1[2b10(A1)-b12(A1)][2b20(A2)+b22(A2)]η21sinΓ/