基于声全息的超声波与微缺陷耦合声场特性研究

马宏伟, 张一澍, 王 星, 关志阳

(西安科技大学 机械工程学院,西安 710054)

随着航空航天、微电子工业、现代医学以及生物工程技术的发展，对三维微结构(特征尺寸在微米级到毫米级)的需求日益迫切，同时对零件在使用功能、材料特性、结构形状、可靠性等方面的要求也越来越高[1]。测量微缺陷的方法有很多，各有其优缺点。近年来，英国曼彻斯特大学材料学院最新研发的3D X-Ray CT能达到很高分辨率[2]，但是必须把样品切割成很小的试样来进行检测，破坏了工件结构，无法做到无损检测。而原子力显微镜(Atomic Force Microscopy, AFM)[3-4]只适用于检测工件的表面缺陷。最近研究的原子力声显微镜技术(Atomic Force Acoustic Microscopy, AFAM)[5-6]能够对亚表面缺陷以纳米级分辨率成像，但是同样没有穿透力，不能对工件内部缺陷进行检测。

在常规超声无损检测中，通常通过分析声场与缺陷相互作用后的声波来评价缺陷，因此，得到与缺陷作用后的声场特性是实现缺陷超声检测信号分析的关键。而在实际工作中，被检测部件的厚度相对较薄的比较多，例如航空件。根据传统的超声理论，在探头的近场区之内，单频连续波声轴线上的声压分布是有起伏的，所以无法对缺陷进行准确的定量。近场声全息(Nearfield Acoustic Holography,NAH)是一种用于声源识别定位和声场可视化的先进技术[7-8]，它通过测量包含倏逝波的近场数据，不仅可以重建出声源的表面声压和法向振速，而且还能对整个三维声场中任意点处的声压、质点速度、声强、声源辅射声功率和远场指向性等一系列声学量进行重建和预测[9]。本文基于角谱法模拟超声检测的过程，根据工件几何结构建立算法模型，通过编程计算得到超声波与工件内部微缺陷耦合的声场特性，并与有限元仿真结果进行对比，通过实验得出相应结论。

1 近场声全息原理

对于声源附近的声场，活塞上不同部分辐射的声波到达观察点时，其相位与振幅都不相同，因而干涉图像比较复杂。计算这种声场在数学上比较困难，而且不能得到简明的解析表达式。尽管角谱分析亦可以直接用于换能器发射声场的模拟，但是在数值计算中需要对快速震荡的贝塞尔函数进行无穷积分，该算法在满足收敛条件时，积分上限的取值会影响计算的周期和结果。在Rayleigh-Somerfield积分的基础上，已经开发出许多近场声全息重构方法[10-12]。其中基于空间Fourier变换的NAH技术，其理论上易于理解，算法和实验容易实现。由近场声全息的预测过程可知：若已知声源面处zs的声压分布，可以计算出距离声源dz处平面zH上的声压。平面近场声全息的基本预测公式为：

[p(x,y,zs)]GD(kx,ky,dz)}

(13)

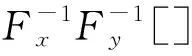
利用NAH计算活塞中心声轴线上的倏逝波声压幅值随距离zd变化情况，如图1所示。可以看出，NAH计算结果与角谱法计算结果基本吻合，但随着距离的增大，NAH计算结果产生较大误差，其相对误差随距离变化关系如图2所示。分析其误差来源主要为：在对波数域进行离散时，考虑到角谱法计算公式中的积分上限，对采样间隔的选取决定了参与计算的有效波数的范围，进而影响到计算结果。通过计算，当zd=0.004 m时，倏逝波已衰减至初始的40%以下，此时的相对误差为6.2%，说明在倏逝波有效传播距离范围内，采用NAH法计算声轴线上的倏逝波声压分布能够得到较为精确的结果。

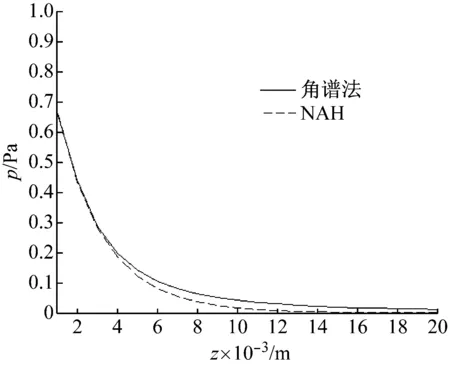
图1 声轴线倏逝波声压分布

Fig.1 Acoustic amplitude distribution of evanescent wave on acoustic axis

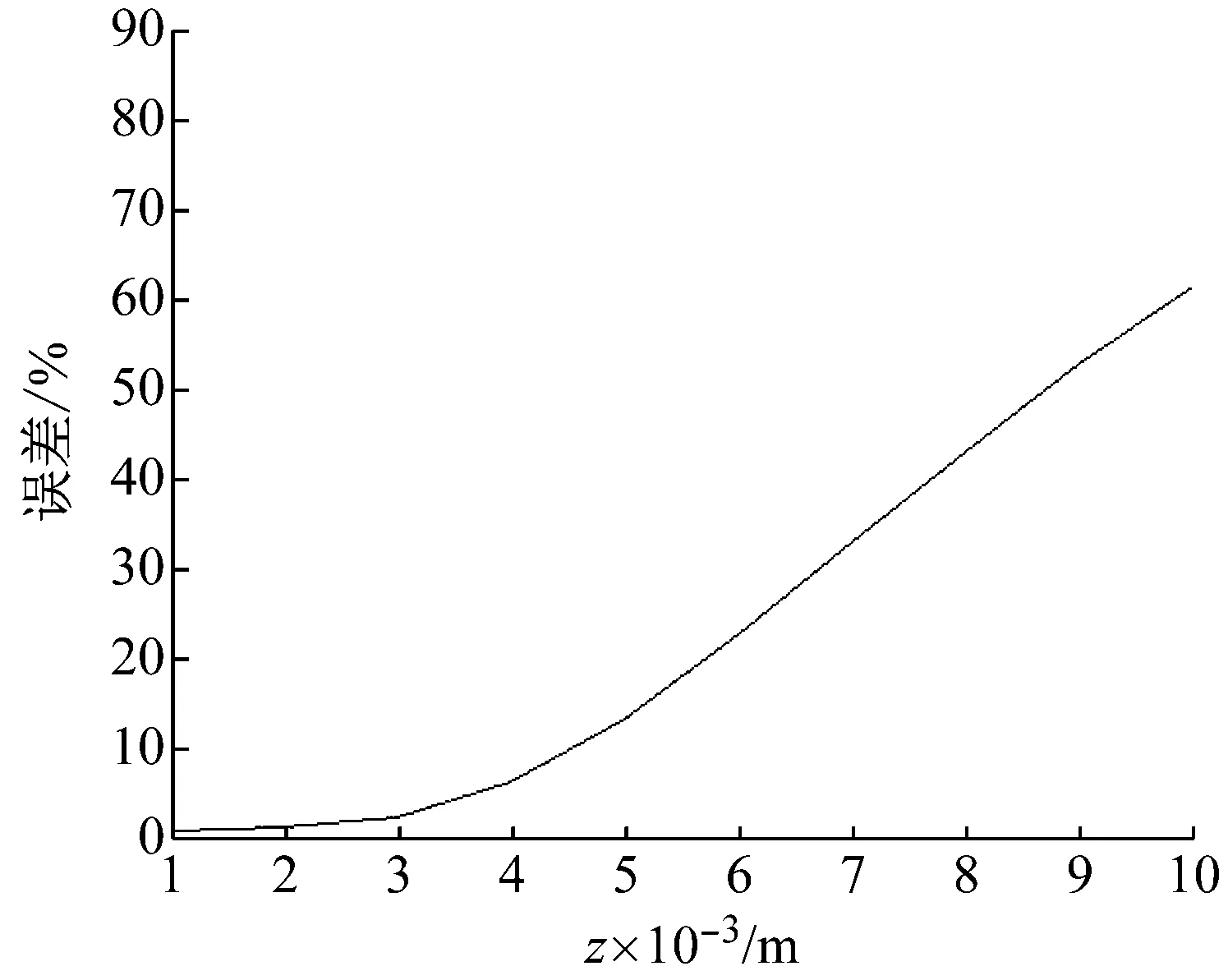
图2 不同距离下的计算误差曲线

2 超声波与微缺陷耦合的声场计算

2.1 计算模型

在小振幅声波的假设条件下，声波在介质中的传播规律可以看作是线性的。如图3所示，在厚度为h的铝薄板前表面存在半径为r、深度为d1的平底孔缺陷。设圆盘声源半径为a，声源面为Z0，平面Z1(与平底孔后端面相切)到工件薄板后表面Z2距离为d2。

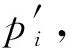
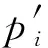
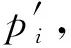
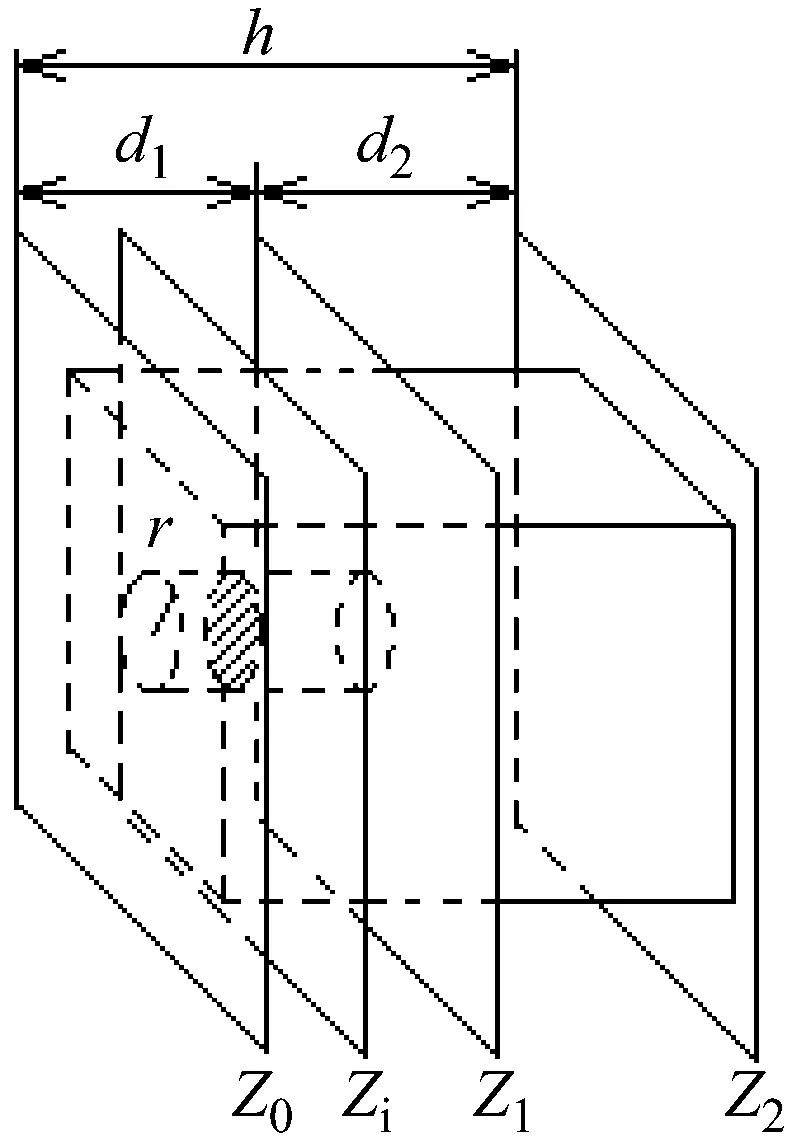
图3 平底孔缺陷算法原理示意图

图4 平底孔缺陷算法流程

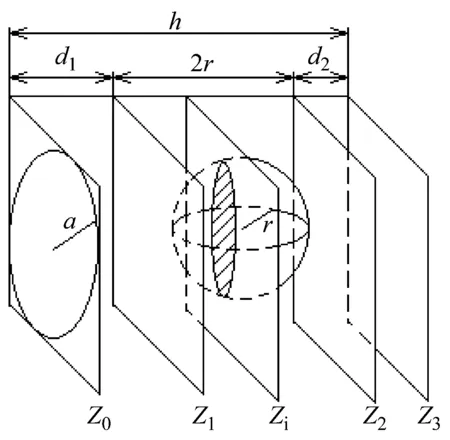
图5 气孔缺陷算法原理示意图

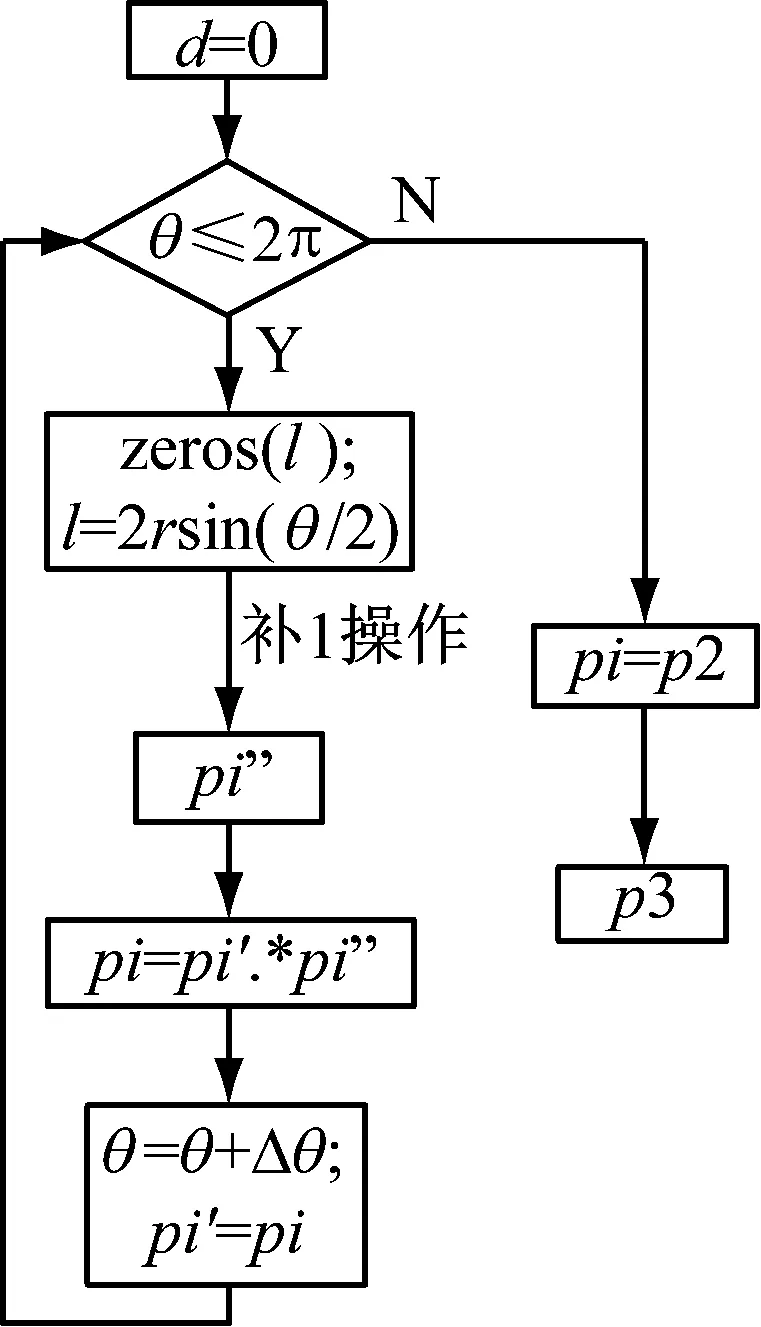
图6 气孔缺陷算法流程

2.2 声压分布计算

按照上述理论，以平底孔缺陷为例，研究超声波在含有微缺陷薄工件内部传播，以及到达工件表面处的声场特性。铝薄板厚度为0.3 mm，平底孔缺陷直径为0.05 mm，深度d1=0.1 mm。设圆形换能器的直径为12.7 mm(0.5in)，激励信号采用频率5 MHz，持续时间为3周期的正弦波，加汉宁窗调制以接近真实信号。从工件前表面Z0进行超声激励，利用角谱法计算工件后表面的声场分布。图7中，(a)～(c)分别为超声波传播至如图2所示的Z0、Z1以及Z2处的声压分布俯视图，(d)为工件内部不含孔洞缺陷时，超声波传播至工件表面Z2的声压分布俯视图。此外，对在工件内部是否含有缺陷时，其中心轴线上不同波数成分的声压分布进行计算，结果如图8所示。

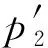
(a) Z0面声压分布

(b) Z1面声压分布

(c) Z2面声压分布

(d) 不含缺陷时Z2面声压分布

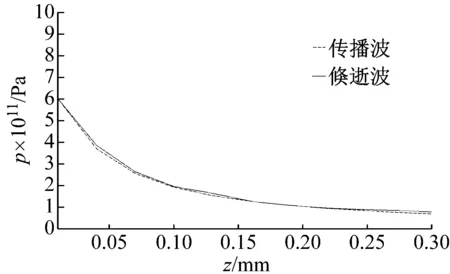
(a) 不含缺陷时轴线声压分布

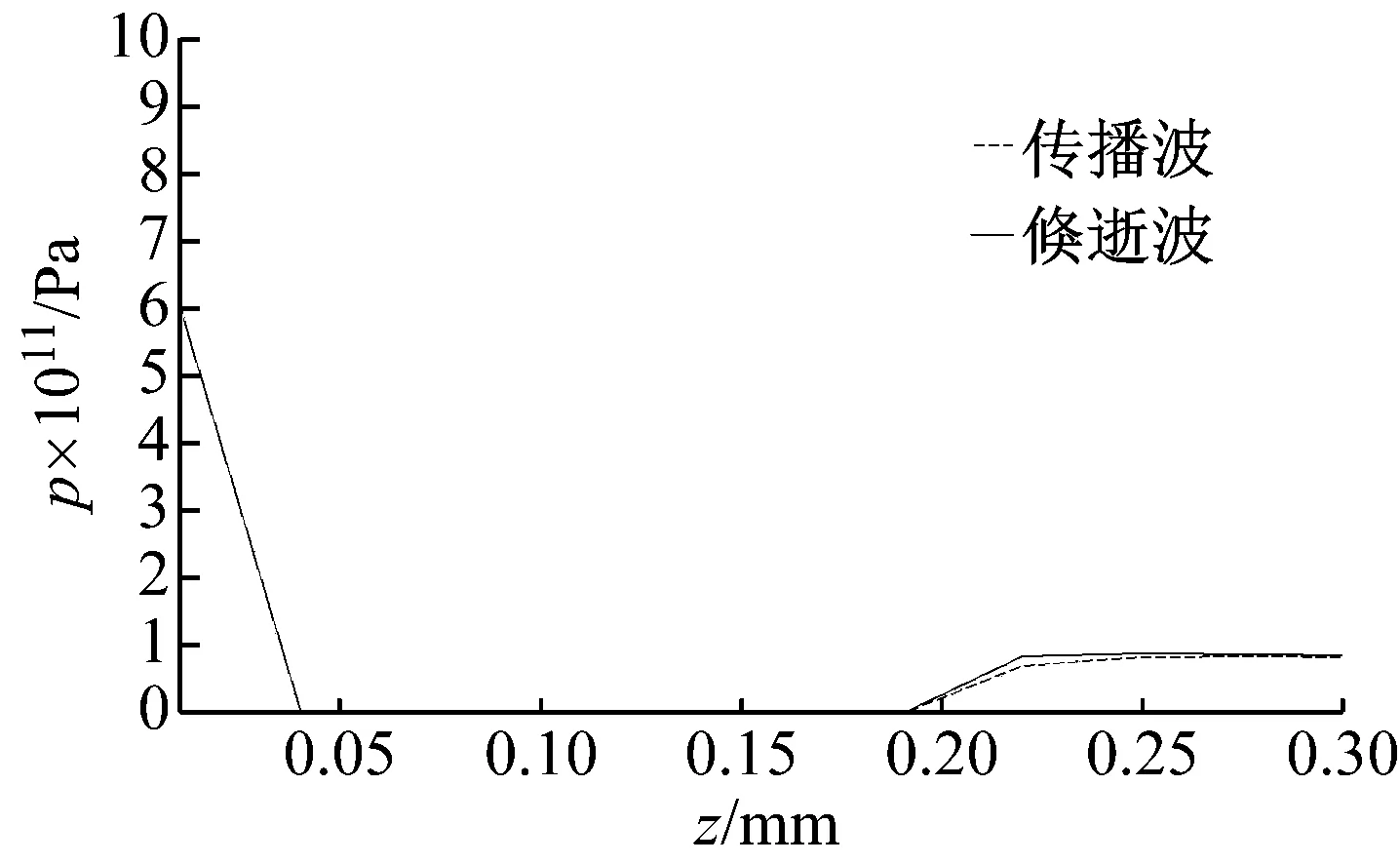
(b) 含缺陷时轴线声压分布

Fig.8 Distribution of sound pressure in the center axis of the workpiece

3 有限元分析

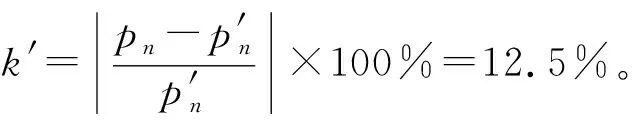
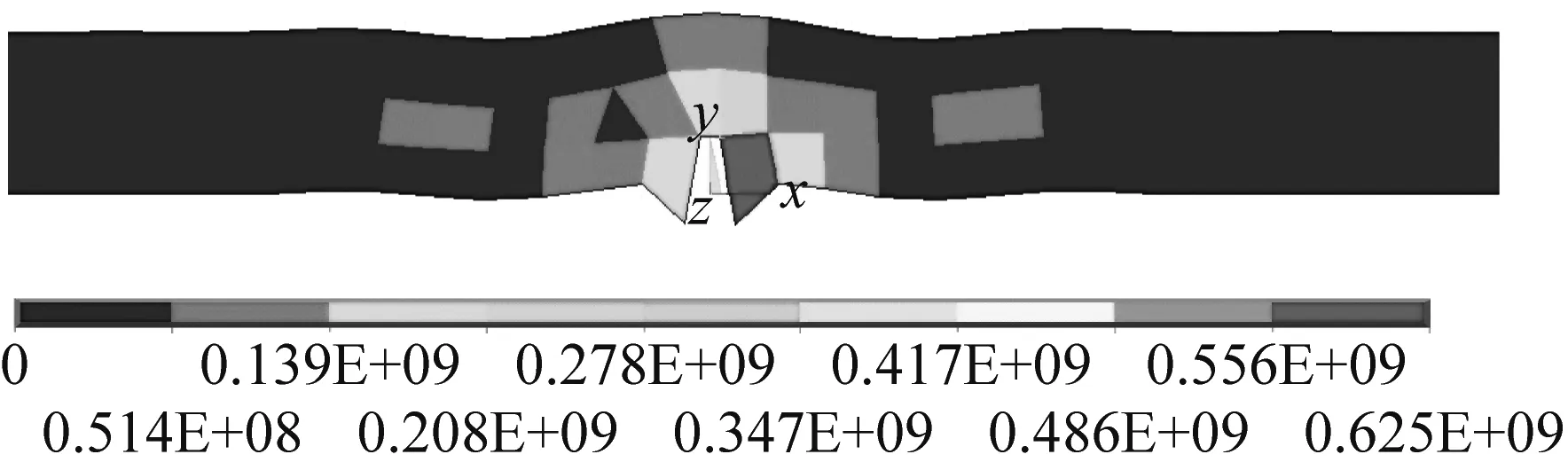
(a) 含有缺陷的工件表面声压分布

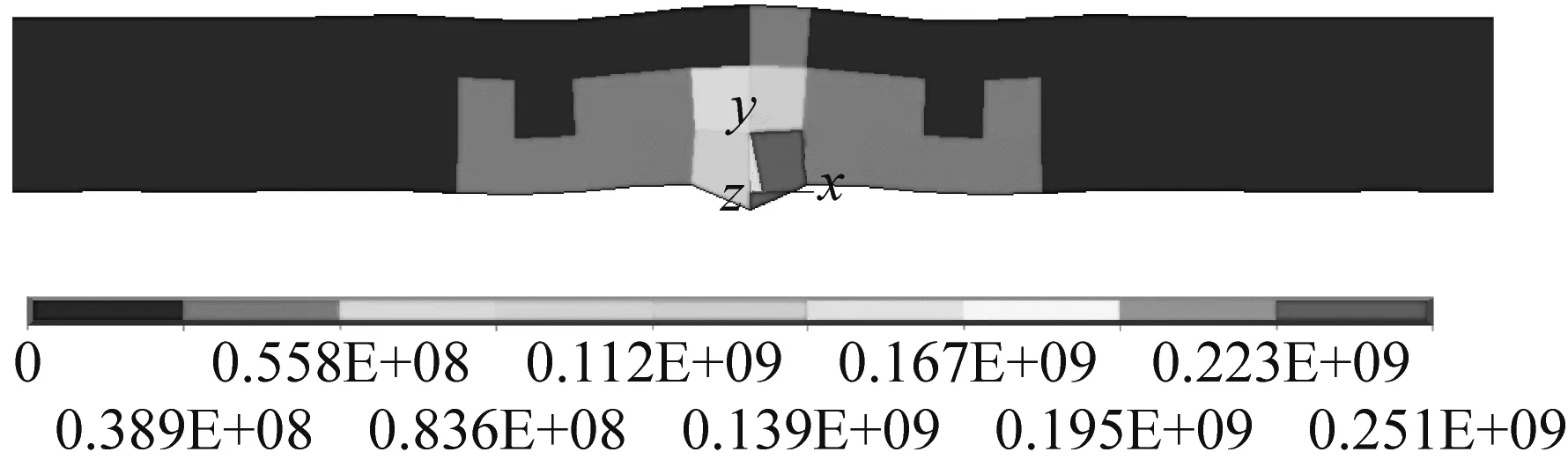
(b) 不含缺陷的工件表面声压分布

Fig.9 Transient sound pressure distribution on the surface of the workpiece

4 结 论

本文基于NAH理论，提出一种超声波在薄板结构中传播并与微小缺陷耦合的声场迭代计算方法，并与有限元仿真进行对比，互为验证。其计算结果表明：基于NAH的迭代算法可以准确地反映近场声压在微结构中传播并与缺陷耦合的分布规律，NAH在数值计算中使用了二维FFT，缩短了计算时间，其声场预测过程尽管存在一定的误差，但是在倏逝波的有效传播距离内能够获得较为精确的计算结果。该方法对于建立超声波与微缺陷耦合的数学模型提供了全新的思路和有效的计算手段，便于人们更深入地理解超声波在介质中传播的过程，进而能够更加准确、可靠地对超声检测结果进行评价。