基于遗传算法的输电线路覆冰灾害应急响应物资储备决策 优化模型*

何帔雨，李 鹏，谢汝生，张松海，蒋建波，曹 敏

(1.云南大学 信息学院，云南 昆明 650091；2.云南电网有限责任公司电力科学研究院，云南 昆明 650217)

0 引言

我国云、贵、川、渝、湘、陕等低纬度高海拔地区，由于地形地貌复杂，气候环境多变，每年冬季在微地形和微气候的共同影响下经常发生冰冻灾害[1-2]，严重覆冰过程将导致架空输变电系统金具损坏、导线断股、杆塔折损、绝缘子翻转破裂等机械事故，或引发绝缘子污闪、舞动闪络、脱冰闪络等电气事故，极大地威胁着输电线网络的正常运行[3-4]。因此，如何根据气象部门提供的气象预报信息及时做出抗击冰冻灾害应急响应，减小对电力网络的影响，已成为亟需解决的问题[5]。但由于云南、贵州、湖南等低纬度高海拔地区冬季冰雪封山，地形地貌复杂，交通状况不佳，因此要及时调配应急相应物资进行事故抢修或维护检修较为困难，且抢险期间正值春运高峰期，而目前电网部门应急物资紧急采购、征用、调拨和配送机制不够完善，存在着物资存储设施不足、布局不尽合理、储备方式单一、数量偏少等弊端。因此必须根据气象部分的预报信息，及时做好物资储备工作。

目前，已有国内外学者对抢险救灾和备品备件决策做了大量的研究。袁仲熊等[6]以备品备件的采购、存储以及缺货成本为基础，提出了用于指导最佳采购量的电网抢修备品备件库存模型；李世停等[7]针对在舰船的部件在航行时段是不可维修的条件下，提出了基于可靠性的舰船备件动态规划决策优化模型；吴在栋等[8]以河流的突发污染为背景，建立基于Dijkstra算法的多目标多约束应急物资调度模型；Ayush等[9]用模因算法来优化车队系统的维修和备件决策水平，并用遗传算法所求解的结果与之做了对比；Ren 等[10]通过灰色局势决策分析，根据当前的维修水平划分来确定相应的备件种类和数量；赵洪山等[11]针对风电机组部件的备品备件库存问题，提出了基于(s,Q)策略的库存优化模型。

根据已有文献，本文针对输电线路覆冰灾害应急响应物资储备问题，提出了基于灾害预警信息的物资储备模型。此模型主要根据天气部门的气象播报来推测覆冰灾害时间段和程度，由此来提前对应急物资做好储备，不仅解决了以往由于地理环境、天气情况等因素对抢险物资配送的安全性和及时性问题，还能使经济耗费降到最低。以云南某供电局的冬季应急物资储备为例验证模型的有效性，同时证明了此模型具有提高电网部门应对冰冻灾害和经济效益的能力。

1 遗传算法决策优化模型

遗传算法是1种基于生物进化理论的优化算法[12]，对于1个需要优化的问题f(x),遗传算法将每1个决策x等同于染色体的基因编码，经过不断的基因重组和变异等操作，寻找最优解。

1)初始化种群。随机产生1个初始化种群M={m1,m2,,mn},对该种群中的每个个体的染色体进行编码。

2)适应度计算。适应度大小表征了个体的生存能力。使用适应度函数f(t)来评估种群M中每个个体的适应度大小，用fi代表个体mi的适应度。

3)亲代选择。根据种群个体的适应度计算出每个个体被选择为亲代的概率。其选择概率如下：

(1)

4)基因交叉重组。将选择的染色体mi和mj进行基因重组。重组后的染色体分别为mi′，mj′，其重组后的编码如式(2)所示。式中a为重组因子，且a∈(0,1)。

(2)

5)基因突变。生成的新染色体编码序列中的某一位编码xi有一定的概率发生变异。

重复步骤2)～5),直到完成最大迭代次数时终止操作。

2 覆冰应急物资储备模型

2.1 问题描述

覆冰灾害中抢修材料和消耗品是覆冰抢险救灾的重要物资，主要包括导线、天线、拉线、绝缘子串、线夹、塔材和变电站的电流互感器、支柱瓷瓶等输变电设备。同时也包括给除冰人员配备的除冰工具和保障工具，如竹竿、绝缘棒、橡皮锤、照明设备、保暖设备(衣服、鞋子)等。

根据云南东北部某供电局近几年提供的数据，覆冰灾害发生主要集中于11月末至第2年3月初的约5个月时间里，如何确定每个月对输变电设备、除冰工具和保障工具的采购量，使得既能满足每月的需求量，保证一定的应急物资安全，又能使采购成本和存储费用达到最小，是科学储备和科学管理物资需要解决的问题。

2.2 建模及求解过程

1)数据定义[13]

sk为第k阶段开始的物资存储数，是状态变量，万套；uk为第k阶段的采购数量，万套，是决策变量；qk为第k阶段的需要量，万套；ck为采购单位成本(因为供求关系的变化，采购成本为变数)，元；rk为每月的需求量，万套。

2)约束条件

应急必需品采购数量以10的倍数进行采购，公司每月最多采购Pmax单位；存储费用为每单位Tp。每个月的需求量和每件应急必需品的单位采购成本如表1所示。

表1 月需及单位成本Table 1 Monthly demand and unit cost

3)数学模型

总费用=每月的采购费用+库存费用，即目标函数：

minz=(c1u1+c2u2++c5u5) +Tp(s1+s2++s5)

(3)

下月初库存=本月初库存量+本月采购量-本月需求量。各月的具体情况如表2所示。初始月为准备期，初始库存由给定值a确定，s1=a。

表2 每月需求情况Table 2 Monthly demand situation

3月份之后，气候回暖，与覆冰应急相对应的物资消耗将为零，得s6=0。这是隐含的约束条件，是问题的约束边界。每月的最大采购限额为Pmax，采购量限制为10的整数倍，可令uk=10m，m为整数且10m≤Pmax。最终得到的数学模型：

(4 )

3 基于遗传算法的覆冰应急物资储备优化模型

本文提出的基于灾害预警信息的物资储备遗传算法模型总体框架如图1所示。该模型首先根据气象部门给出的覆冰灾害月度预报信息，依据线路规模和抗灾经验确定覆冰灾害应急物资需求数量，参与每月月初的采购决策，决定物资的采购量，作为该模型的辅助决策与辅助分析。

模型中，以覆冰应急物资储备的最小成本为目标函数，以每月采购量为决策变量，结合每月的存储量、需求量等因素建立多约束条件。在遗传算法中，初始化相关参数，并以目标函数的倒数为适应度函数，经过不断迭代，最终找到每月采购数量的最优决策和目标函数的最优值。其遗传算法的伪代码如下：

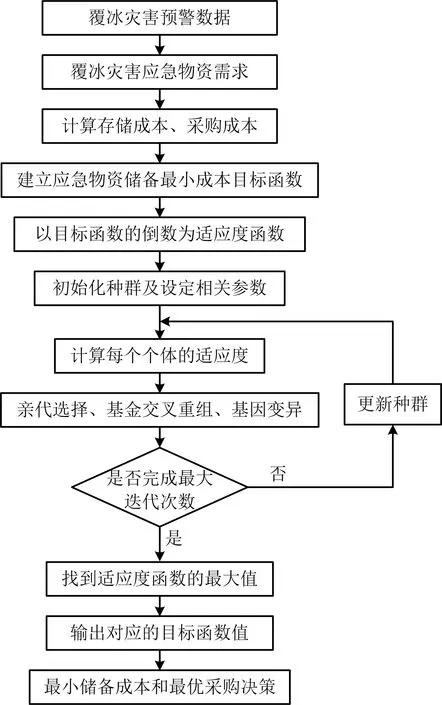
图1 模型总体框架Fig.1 Model overall framework

{pc：基因交叉重组概率 pm：基因变异概率

m：种群大小g：最大迭代次数

初始化pm，pc，m，g等参数。随机产生初始种群pop

do

{对每个染色体进行二进制编码

以模型中的目标函数的倒数为适应度函数

计算种群中每一个体的适应度fi

初始化空种群newpop

do

{

根据选择概率从种群中选出2个亲代

if ( random ( 0 , 1 ) < pc )

{

对2个亲代个体按交叉概率进行交叉操作

}

if ( random ( 0 , 1 ) < pm )

{

对2个亲代个体按变异概率进行变异操作

}

将2个新个体加入种群newpop中

}

until (m个子代被创建 )

用newpop取代pop

}

until (繁殖次数超过g)

找到适应度函数最大时对应的目标函数值

output (应急物资储备最小成本及5个月的最优采购决策)}

4 结果测试及分析

4.1 遗传算法优化

以除冰人员保障物资(衣服、鞋、手套等)为例，假设初始库存为20万套，库存成本为2元/套，其每月采购的数量最大值为150万套(Pmax=150)，根据以往的覆冰情况和物资需求统计数据，11月至第2年3月物资的需求情况和各月的采购成本分别如表3和表4所示。

表3 每月物资需求数量Table 3 Monthly demand for materials

表4 每月采购成本Table 4 Monthly purchase cost

通过遗传算法对上述模型进行优化。在遗传算法中，种群大小为200；基因交叉重组概率为0.9;变异概率为0.05；迭代次数为300。遗传算法优化的迭代收敛图如图2所示，所得出的最优决策如表5所示，总成本最小值为25 380元。

4.2 动态规划优化

动态规划是运筹学的1个分支，是求解决策过程较

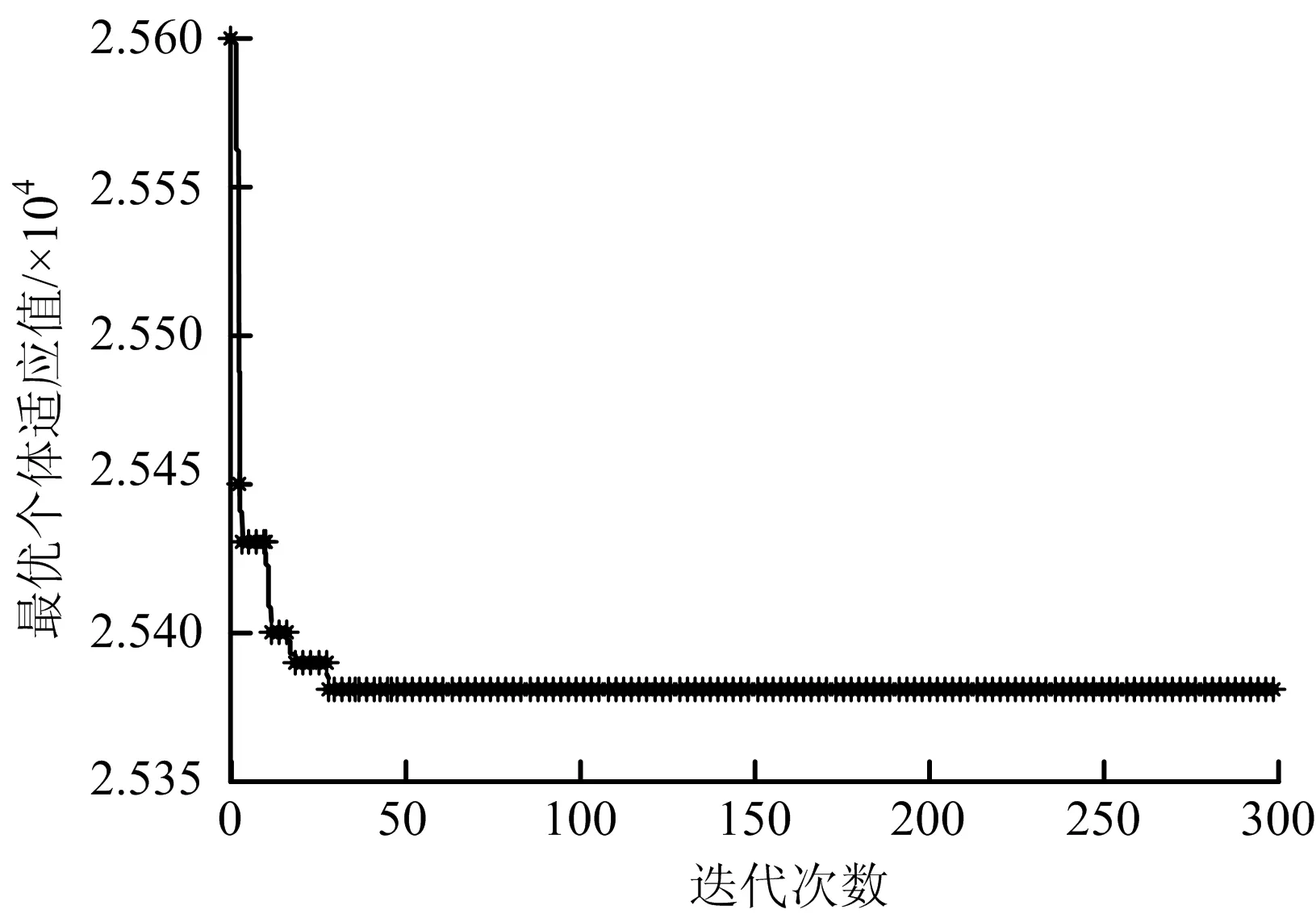
图2 遗传算法迭代收敛曲线Fig.2 Genetic algorithm iterative convergence graph

月份需求量/万套117012150011002130030

为优化的数学方法。基本思想是将待求解的多阶段问题分解为单阶段决策问题，利用各阶段之间的关系，逐个求解，前一子问题的解为后一子问题的求解提供有用的信息。

将该模型动态的视为按各个阶段(各月)先后做出决策(采购量)的过程，在每个月做决策时，不能仅考虑本月的费用(阶段指标)，因为本月的决策会对以后的各月的决策产生影响，应优先考虑从开始到结束的总费用(总指标)，而每月的决策可以依赖于各月月初仓库中的存货量以及需要量(对以往数据作分析和预测)，而与以前各月如何造成这一存货量的情况无关(无后效性)。其动态规划模型框架如图3所示。

图3 动态规划模型框架Fig.3 Dynamic programming model framework

由图3可知，动态规划分为5个阶段。根据逆序解法，第1阶段为11月份，第2阶段是12月份，依此类推。通过动态规划方法对上述模型进行决策优化，求解的每月最优采购决策如表6所示，总成本最小值为26 430元。

表6 动态规划优化结果Table 6 Dynamic programming optimization results

通过对遗传算法和动态规划优化的实验结果比较分析可知，二者5个月的总采购量是相同的，由于受每个月的采购成本、存储成本的不同，二者在各月的采购量上产生了差别，最终导致了在总成本上的差异。在都满足约束的条件下，从总成本的角度来看，遗传算法所求得的采购决策优于动态规划，通过动态规划结果也验证了遗传算法在此模型上的正确性和有效性。

5 结论

1)针对电网物资储备中的易耗品、消耗品和应急保障物资提出了预警模型。根据天气预测，提前对应急物资做以储备，解决了应急物资采购、运输等方面的难题，也使得电力部门在应急物资储备设施和布局方面更加合理，消除储备数量偏少等弊端，最终提高应对电网灾害的可靠性和及时性。

2)根据覆冰预测计算，物资还处于实验阶段，但是随着覆冰预测模型的精确，月初物资的需求量也将逐渐明确，对成本的控制也会越来越精确。