基于能量理论的煤与瓦斯突出机理探讨*

师皓宇，马念杰，许海涛

(1. 华北科技学院 安全工程学院，北京 101601；2.中国矿业大学(北京) 资源与安全工程学院，北京 10083)

0 引言

煤与瓦斯突出是世界范围内煤矿中最严重的灾害之一[1]，国内外学者对煤与瓦斯突出问题开展了大量研究，提出了诸多的假说和理论。如瓦斯主导作用假说认为煤体内的高压瓦斯是突出发生的主要因素[2]；地应力主导作用假说认为当工作面接近储存有高应变能的岩层时，这些应力将煤体破碎引起煤与瓦斯突出[3]；化学本质作用假说认为煤与瓦斯突出是煤体内部本身的特殊化学变化引起的[4]；综合作用假说认为突出是由地应力、瓦斯压力及煤的力学性质等因素综合作用的结果[5-6]，认为煤与瓦斯突出要受到地应力、瓦斯压力的大小、煤质分布、顶底板岩性和采掘方式、时间与空间条件的控制[7-8]。以上理论对煤与瓦斯突出机理的发展均有很大的推动作用，但仍有不尽如人意之处。如瓦斯主导作用假说中的“瓦斯包”尚未在煤层中发现；煤与瓦斯突出的危险区域未必处于高地应力场；综合作用假说对煤岩体的破坏条件缺乏判断依据，对抽象的能量问题难以进行量化分析。

煤与瓦斯突出时的煤体破碎、煤体抛出、摩擦生热、震动声响等均需要能量参与其中[9-12]。瓦斯体积膨胀所释放的势能和煤岩体弹塑性状态转换时释放的应变能则可能是煤与瓦斯突出的能量源，文献[13]提出估算煤系地层中的弹性能和煤层中瓦斯的势能的计算方法；文献[14-15]建立了煤与瓦斯突出强度能量评价模型，并用于平煤矿区的突出能量计算；文献[16-17]认为煤与瓦斯突出主要受控于煤体的应力分布以及孔隙和裂隙中的瓦斯压力。

本文拟从理想气体状态方程着手推导瓦斯体积膨胀过程中的对外做功方程，依据煤壁前方应力分布规律推演回采前后煤岩体的应变能释放机理，揭示煤与瓦斯突出的能量来源与作用机理。

1 煤中瓦斯能量势能计算

图1为瓦斯膨胀做功示意图。

图1 瓦斯膨胀做功示意Fig.1 Schematic diagram of gas expansion work

根据理想气体状态方程，假设当瓦斯涌出时其温度不变，则：

p1v1=pxvx

(1)

式中：p1为压缩状态时的压力，Pa；v1为压缩状态时的体积，m3；压缩状态时的压力和体积如图1中OA段所示；px为气体膨胀到一定程度时的压力，Pa；vx为气体膨胀到一定程度时的体积，m3；气体膨胀到一定程度时的压力和体积如图1所示OB段。假设瓦斯突出后，煤岩体沿某个方向移动，体积为v1的瓦斯的底面积为S，m2；长度为l1，m；v1=S×l1；膨胀后的长度为lx，m；vx=S×lx，则：

(2)

(3)

瓦斯突出后，气体能量完全释放，p0为大气压，如图1所示OC段，即px=p0=0.1 MPa，则此时瓦斯体积为：

(4)

(5)

当气体由A点膨胀至B点位置时，气体对外做功Wg为：

(6)

计算得：

(7)

当瓦斯压力减小至大气压时，可认为瓦斯能量完全释放，即由A点膨胀至C点，瓦斯对外做功为：

(8)

因此，单位体积的能量释放与气体形状、路径无关，只与其始终的状态有关，即压力和体积。假设煤壁中的孔隙率为n，煤体内的瓦斯均完全解析，则体积为vc的煤体中含有瓦斯的体积为nvc，当煤处于弹性状态时或完好状态时，瓦斯聚集于煤壁内，当煤壁发生塑性破坏时，瓦斯可能与煤体一起突出，此时单位体积煤体内瓦斯对外做功为：

(9)

2 煤壁前方释放应变能

将煤壁前方的应力状态简化为平面应力状态，其采场前方极限平衡区和弹性区理论对工作面前方支承压力分布情况和受力状态大致如图2所示。

建立极限平衡方程[18-19]：

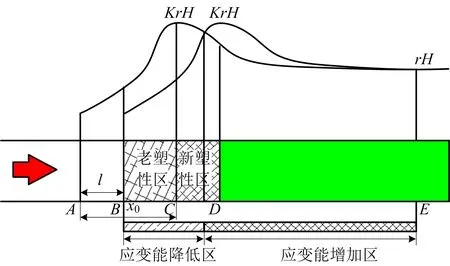
图2 进尺前后煤体状态变化Fig.2 Change of coal status before and after mining

(10)

依据莫尔-库仑强度准则，塑性区内支承压力：

(11)

式中：f为层间的摩擦系数；φ为煤体内摩擦角，(°)；x为塑性区内任一点到煤壁的距离，m；M为采高，m；τ0为煤岩体的黏聚力，MPa；τ0cotφ为煤体自承力，MPa；σx为水平应力，MPa。

则支承应力峰值点到煤壁的距离：

(12)

式中：K为应力集中系数；γ为上覆岩层容重，kN/m3；H为煤层埋深，m。

如图2所示，当煤壁进尺后，煤壁内的应力峰值随之前移，从图2中的C点移至D点位置；老塑性区部分被切割(AB段)，同时产生新的塑性区(CD段)，煤体大致呈3种状态，老塑性破坏区(BC段)、新塑性破坏区(CD段)和弹性区(DE)。老塑性破坏区BC段内瓦斯已经部分释放，而原先因处于弹性区(CD段)而被限制的瓦斯因塑性破坏而被释放，煤是1种复杂的具有孔隙、裂隙结构的多孔介质，对瓦斯具有很强的吸附性，其吸附和解析过程主要受煤的温度与压力作用影响[20-21]。因此，塑性区的产生致使浅部煤体的约束力减小，而可能原先吸附于煤体的瓦斯也开始析出，涌出更多的瓦斯，瓦斯压力增大，当塑性区煤体的约束力小于瓦斯压力时，瓦斯积聚势能的释放将协同老塑性破坏区的煤体共同抛出，从而形成煤与瓦斯突出。

应变能释放区和应变能积聚区的范围要受到三向主应力和煤岩体的弹性模量和泊松比共同影响。根据能量密度公式：

(13)

则一定区域内的能量变化值W为：

(14)

式中：Ua，Ub分别为进尺前后煤岩体的能量密度，J/m3；σ1，σ2，σ3分别为煤岩体的最大、平均、最小主应力，MPa；E为弹性模量，MPa；μ为泊松比；W为能量变化值，J；当W>0时，该区域释放应变能Wr，J；当W<0时，该区域积聚应变能Wa，J；即释放区域所释放的应变能部分转移至应变能集聚区域，部分瓦斯能量转化为煤体动能释放出来。煤壁前方应变能释放值We应为释放区域积聚区的应变能差值，即：

We=Wr-Wa

(15)

根据蝶形塑性区理论，区域主应力场的最大主应力达到某一临界值时，蝶形塑性区最大半径为无穷大；当区域主应力场的最大主应力超过围岩单轴抗压强度后，随着最小主应力的减小，蝶形塑性区的最大半径也可以达到无穷大。如果围岩具备这种塑性区无限扩展的条件时，则参与突出的瓦斯体积和煤体体积可能无比巨大，产生的冲击灾害或瓦斯突出将是灾难性的[12,22]。

3 煤与瓦斯突出动能

由于煤体开挖，导致煤壁前方煤体应力重新分布，导致塑性区边界随之前移，部分应变能We与瓦斯应变能Wg对煤体做功而使煤体具有一定的动能，当能量转化效率为η(值介于0和1之间，无量纲)时，则对煤体的做功而产生的动能E为：

E=η(Wg+We)

(16)

瓦斯释放的能量作用于煤体时，煤体可获得向外喷射的动能；煤体的密度为ρ，煤体单位厚度为1 m；新塑性区的长度为l，m；极限平衡区长度为x0，m；采高为M，m；则突出煤体质量为m=x0Mρ，瓦斯释放体积为vr=nlM，煤体前方释放的应变能为We，则煤体获得的动能存在如下关系：

(17)

则煤体速度v为:

(18)

由式(18)可以看出，当瓦斯突出时，煤体获得的速度随着瓦斯含量的增大而增大，随瓦斯压力的增大而增大，随煤岩体应变能释放值的增大而增大。当速度较大时，能够形成突出效应；当速度较小时，不能形成突出效应。由于在实际计算中We值难以直接进行理论计算，当略去We后则有如下结果：

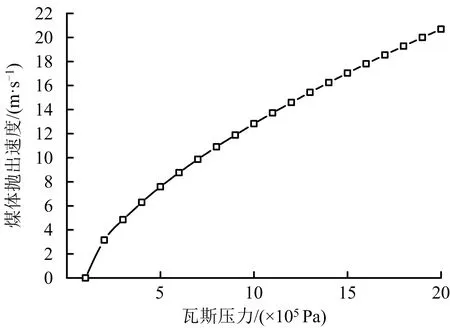
图3 v-p关系Fig.3 Relation graph of v-p

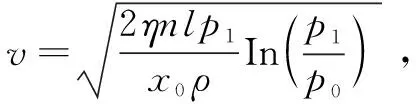
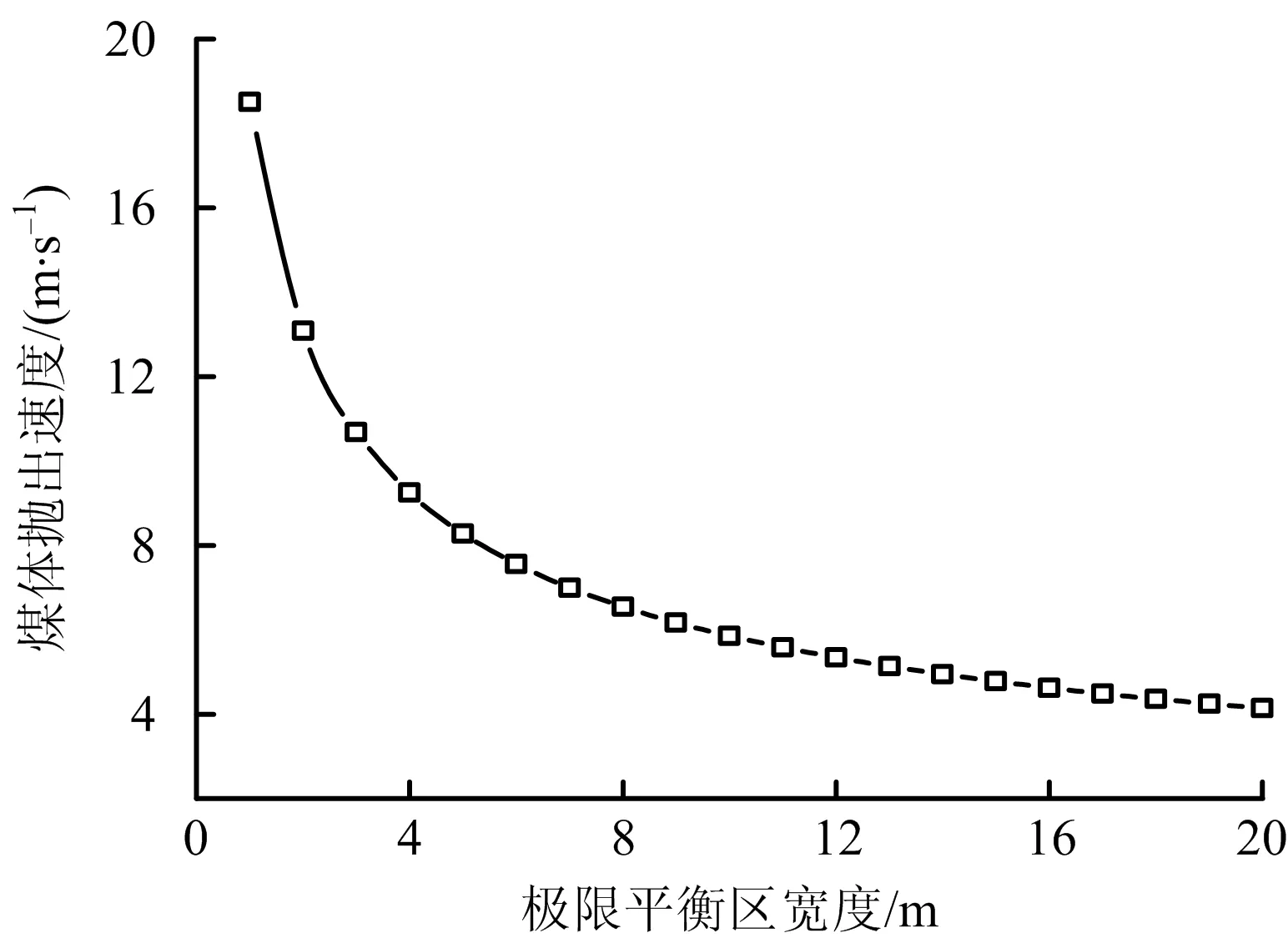
图4 v-x0关系Fig.4 Relation graph of v-x0

4 实例验证

淮北芦岭煤矿是个煤与瓦斯突出矿井，自矿井投产以来，共发生煤与瓦斯突出20次，2002年主要开采8号和9号煤层，其中8号煤厚7.36～11.53 m，平均9.77 m；9号煤层厚0～3.59 m，平均2.13 m；煤层倾角平均为18°～21°。开采水平为-590 m，实测煤层瓦斯压力为2.6 MPa，瓦斯涌出量为17 m3/min；采区瓦斯涌出量为31.2 m3/min，其中，风排瓦斯量为29.2 m3/min，抽放量为2.0 m3/min。芦岭煤矿曾发生1次特大型煤与瓦斯突出事故，该事故发生在Ⅱ81采区，突出煤岩量8 729 t、瓦斯量93万m3；突出煤体抛出最远240 m，累计添堵巷道796 m，添堵体积7 935 m[23]。

按照式(2)可知，瓦斯突出前的体积应为3.6 万m3，突出后的瓦斯压力按大气压(0.1 MPa)计算，带入式(8)，经计算，Wg为3.05×1011J，抛出煤体质量为8 273 t，按能量的50%用于煤体做功，则煤体获得平均速度为135.7 m/s，按巷道高度3 m计算，按底部煤体斜向上抛射，按照抛物线公式计算，最大抛出时间约为1.6 s，最远抛出距离约为217 m，略小于此次最远抛出距离。因此，此次瓦斯突出事件中，除了瓦斯势能的释放外，还有煤岩体应变能参与了本次突出事件。

基于以上理论和案例分析，针对煤与瓦斯突出提出以下防治措施：①通过钻孔卸压或瓦斯抽放减小瓦斯压力；②增加极限平衡区距离、减小截深；③通过矿压控制，避免巷道或工作面围岩出现瞬间的、大范围的蝶形塑性破坏。

5 结论

1)具备一定体积的高压瓦斯被限制于未采动区域，瓦斯与煤岩体间的平衡在采动作用下被打破而产生较大范围的塑性区，较高的瓦斯压力就会迅速膨胀，抛出破碎的煤岩体，造成突出。

2)瓦斯气体的膨胀与煤岩体弹塑性状态的变化均会导致巨量能量的释放。瓦斯气体能量释放与气体形状、路径无关，只与其始终状态有关，即释放能量值与瓦斯含量、瓦斯压力正相关。瓦斯突出时，煤体突出速度随应变能释放值的增大而增大。

3)对于煤与瓦斯突出，提出以下防治措施：一是通过钻孔卸压或瓦斯抽放减小瓦斯压力；二是增加极限平衡区距离、减小截深；三是通过矿压控制，避免巷道或工作面围岩出现瞬间的、大范围的蝶形塑性破坏。