浅议构造法在初中数学解题中的有效运用

李 斐

(江苏省泰兴市新街初级中学 225474)

一、重视题意分析

分析题意是大多初中学生所必须要掌握的一项内容，也只有弄清题目的具体意思，并据此找到已知条件、未知条件、隐含条件等，才能理清条件与问题之间的关系，并尽快找到问题的切入点以及解题的具体思路.在采取构造法引导学生进行解题的过程中，教师应重点关注学生对题意的分析与理解情况，并据此判断学生在逻辑分析与题意分析方面存在的问题，并有针对性地调整教学策略，以此不断提高学生的数学解题能力，提高学生的解题效率.

二、找到解题思路

在传统的解题教学当中，大多数教师在解题教学过程中主要是直接给出具体的解题思路，并未意识到学生需要锻炼与培养，如若教师长期给出具体的解题思路，学生必然会产生依赖性，导致其解题能力、题目分析能力一直得不到有效的提高，这对于其今后的学习与发展毫无益处.因此，教师在考虑教学进度的同时必须要重点培养学生的独立解题能力，让其能在解题过程中积极运用所学知识以及题目的有限条件找到解题的思路，让学生的解题能力在不断的锻炼中得到有效的提高.

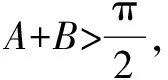
三、重视归纳总结

对于大多数学生而言，数学本身就是一门相对较为难学的课程，没有语文、英语等人文学科那般随心所欲，学生需要根据既定公式、推理模式等进行解题，而且问题最终的答案大多具有唯一性.在新的时代背景下，传统的解题教学模式已经无法适应现代学生的学习要求，教师必须要及时对教学模式进行完善与创新，在丰富学生体验、提高学生兴趣的基础上夯实其解题能力.值得注意的是，构造法既然在初中数学解题教学中具有如此之高的运用价值，教师则必须要充分发挥此种方法的作用与价值，并引导学生做好相应的总结与归纳工作，从而帮助其及时理清知识脉络、完善知识系统，最终促进学生学习与解题能力的不断提高.仍然以上面所提到的题目为例，这个例题涉及到了学生较为陌生的三角函数，为了帮助其尽快找到解决问题的思路、掌握相关的数学知识，并构建良好的知识系统，教师则必须要引导学生对解题过程进行归纳与总结，A学生在解题的过程中运用到了正玄定理与余弦定理，教师可以引导其归纳总结正余弦定理的运用过程与运用方式；B学生的解题思路侧重于函数知识的运用，教师则可以引导其归纳总结与函数相关的知识，并让学生在学习之余多回顾、复习总结的知识与内容，从而在今后解题过程中能迅速从脑海中提取出相应的知识进行解题.除此之外，在有条件的情况下，教师还可以组织学生进行交流分析，让其分享一下总结归纳的具体内容，并通过知识共享的方式来搭建完善的数学知识网络，最终实现合作共赢，从而不断提高其数学学习效果与解题能力.

总而言之，在新的时代背景下，传统的数学教学模式已经无法满足学生们的学习与探究需求，教师在对教学模式进行改革与完善的同时，还应当将构造法纳入数学解题教学过程中，让学生在解题的过程中能做到认真分析与解读题意，并找到多种不同的解题思路，从而尽快求出问题的答案.在这个过程中，学生的解题能力、逻辑思维能力以及知识构造能力均得到了良好的锻炼.除此之外，教师还应重点引导学生归纳与总结解题思路、过程，虽然数学问题千变万化，但终究不离其宗，学生掌握具体解题思路与方法之后，数学知识结构自然建立起来，解题效率也会得到相应的提高.