潜水作用下土壤水盐运移过程
,
(1.中国科学院 东北地理与农业生态研究所,吉林 长春 130102; 2.中国科学院大学,北京 100049)
0 引 言
土壤盐渍化是影响全球温带地区农业生产及生态安全的重要因素之一[1]。已有研究表明,影响土壤盐渍化形成的因素除当地气候条件,还与地下水埋深、潜水矿化度、地表植被和土壤质地等有关,其中,地下水埋深与潜水矿化度是造成土壤盐渍化问题最主要的因素之一[2-5]。温带灌区,大量的灌水抬高地下水水位,使地下水埋深变浅,地下水位上升至临界水位之上时便加速灌区地下水对表层土壤的水分补给,进而加速土壤表层水分蒸发。“盐随水走”,表层土壤水蒸发过程中将地下水及土壤深层的盐分带至地表,造成土壤耕层盐渍化的发生与加重[6]。此外,部分盐渍土区地下水埋深本身相对较浅且矿化度较高,在强蒸发作用的影响下容易引发土壤次生盐渍化甚至盐沼化[7]。无论地下水位本身埋深较浅还是人为作用下抬高,土壤盐渍化形成的根本原因是水盐在土壤中的运动及存储导致。土壤孔隙被水完全充满时,这部分土壤水称为饱和土壤水;土壤孔隙未被水充满,土壤中含水处于非饱和状态,我们称含有非饱和状态水分的土壤区域为非饱和带(包气带),其中的水分为非饱和土壤水,即一般所指的土壤水[6]。近年来,有关土壤水运移动态的研究、水热盐的耦合运移机理、冻结土壤中水分的运移以及地下水-土壤-植物-大气连续体水热盐运移等多学科交叉研究不断涌现[8],而且地下水作用下土壤水运动研究也不断深入,并开展了土壤水盐运移机理的研究,包括土壤水参数的测定及确定,土壤水参数的空间变异性、优先流及能态研究等[9-10]。目前,主要研究方法包括野外实地观测与室内人工控制模拟潜水埋深相结合,发挥计算机软件与数学方程的分析处理优势,对土壤水盐动态进行可视化数值模拟[11]。所有水盐动态模型中,有关盐渍土的水盐动态特性及计算方法的研究尤为深入,并发展形成了以Richards模型为基础的一系列物理经验模型。模型的研究无论是对土壤改良、灌溉和排水设计,还是对于水资源评价等问题均有重要的理论和现实意义[12]。
鉴于地下水对形成土壤盐渍化问题的深刻影响,土壤水盐运移模型对土壤盐渍化机理研究及治理的重要性,本文概括了地下水与土壤水相互作用的动态关系,着重介绍了地下水作用下土壤水分运动与盐分积累的机理。根据水盐运移模型的原理将其分为经验模型、半经验-半机理模型与机理模型,分别介绍相关模型。最后通过地下水作用下土壤水盐动态、水盐运移模型研究及人工控制潜水埋深等内容,对未来水盐运移发展及盐渍土改良做出总结与预测。
1 地下水浅埋区地下水与土壤水的关系
非饱和土壤水是联系地表水与地下水的纽带,是地下水与大气水联系的基础(图1)。不同地区潜水埋深一般不同。潜水面以土壤耕层底部[13](地表以下20 cm左右处,不同地区一般不同)与当地临界潜水蒸发面为水位分割点,将潜水埋深分为3种情况[14-15],即潜水面位于土壤耕层,潜水面介于土壤耕层底部与临界潜水蒸发面之间和潜水面在临界潜水蒸发面之下[16]。
1.1 潜水面位于土壤耕层
潜水面高出土壤耕层底部且在地表未形成径流时,土壤耕层底部以下含水量接近饱和,耕层底部以上土壤含水量相对较高。高地下水位使土壤孔隙几乎被水充满,外来水源易抬高地下水位,此时,土壤水与大气作用强烈,不断的潜水蒸发使盐分在耕层聚集,使地表土壤盐渍化发生或加重[17]。同时,地下水位在耕层底部以上的升降对耕层土壤形成周期性的缺氧环境,在这种环境下,土壤溶质容易迁移,在迁移过程中易发生化学反应。有研究表明,埋藏浅的潜水与非饱和土壤水及大气水作用剧烈,是形成土壤盐渍化及沼泽化的主要原因[18-20]。潜水面位于耕层时,大气降水及灌溉对潜水埋深影响巨大,大尺度上浅水面不易控制[21]。基于此,潜水面位于耕层的土壤水盐动态研究主要集中于人工控制潜水埋深下的土柱试验。人工控制潜水埋深土柱试验限制田间不稳定因素对试验结果的影响,但是由于实验室环境稳定,对实际生产的指导意义只限于理论层面。若为生产实践提供更加可靠的支持需将理论层面研究与大田试验相结合,这些问题有待科研人员通过大区域的生产实践来解决。
1.2 潜水面位于土壤耕层底部与临界潜水面之间
临界潜水埋深是指地下水不能通过毛细作用上升至土壤表层的埋深深度,即潜水参与土壤水分蒸发时可忽略潜水时的埋深。介于耕层底部与临界潜水埋深的地下水对土壤水盐作用影响的问题是学者研究最多,也是关注度最大的内容。潜水面位于该层时(图2),地下水中的盐分随着水分通过土壤不饱和区向上运动,聚集在耕区,导致土壤盐渍化问题加剧[22-23]。受降水与灌溉的影响,土壤盐分随着水分淋洗至土壤底层或地下水,导致地下水矿化度升高。在黄河两岸的引黄灌区、新疆石河子兵团盐碱地、长江三角洲及东北松嫩平原均分布着大量的浅层地下水,地下水与土壤水的相互作用多属于这种情形。同样,浅埋深地下水对土壤水分蒸发也有重要影响[24-25],对土壤剖面水盐含量,水势分布有很大影响。浅埋深地下水可以随着土壤毛细管向上运动并蒸发,造成盐分在地表的大量积累,最终加重土壤盐渍化程度[18]。此外,该层地下水埋深较浅,容易与地表水相互作用,地表水受污染后的入渗容易引起土壤及地下水的污染[26]。
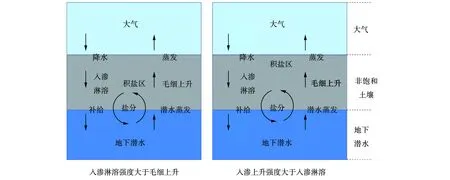
图2 一维状况下土壤水盐交换示意图Fig.2 The diagram of soil water and salt exchange in one-dimensional condition
潜水面位于该层时,土壤水盐动态数值模型模拟结果与实测值的耦合性一般较好[27-28]。学者们已相继建立了在该潜水埋深条件下潜水埋深与土壤水蒸发数值模型,例如阿维里扬诺夫经验方程、清华雷志栋方程以及模拟水盐动态模型的计算机软件,如HYDRUS、MODFLOW等。虽然上述模型能较好地反应潜水埋深与土壤水蒸发的问题,但由于土壤空间异质性的存在,不同地区气候类型、土壤质地及植被状况等均存在差异,导致模型参数选择需要大量观测数据反演推测。对于这种情形,土壤水盐运移模型的发展仍需考虑各个因素对土壤水分蒸发影响的权重。
1.3 潜水面低于临界潜水面
潜水埋深大于临界潜水埋深时,即地下水不能运动到土壤上层的情况。该情况下,地下水与土壤水作用较弱,地表水与地下水一般为单向联系。地表水可通过入渗补给地下水,地下水几乎不能影响地表水。已有研究表明,影响潜水临界埋深的因素除了当地土壤质地、容重和紧实度等基本土壤物理因素外,还与当地气候、植被等因素相关[29]。已有研究表明,从砂砾石到亚黏土,潜水蒸发极限埋深变化在2.38~5.16 m[30]。不同地区潜水埋深临界值为我国土壤水动力学的理论研究提供了重要的背景值。对于埋深大于临界值的潜水,地下水对土壤表层作用比较微弱,对土壤表层水盐运移与溶质运移影响较小,数值模型一般不考虑地下水的作用。
以上3种地下水埋深的情形对土壤水分蒸发的影响已有一定的研究。对于埋深较浅的地下水一般受降水、灌溉和土壤毛细管向上运动与人工活动的影响较大。当潜水面在临界水位以上时,土壤水与地下水相互作用较明显,研究其中任何一个都必然受到另一个因素的制约。同时,由于各种因素所造成的潜水面的变化势必会对土壤含水量、盐分含量与组成造成影响,该过程在实际研究中不可忽视。随着研究的深入,土壤水分运动过程中所受各种势能已经进入科研工作者的视野,从动力机制解释水分运动趋势逐渐成为建模的手段。此外,土壤包气带中水文变化与溶质、热运移也已作为重要的研究内容。
已有模型研究表明,潜水埋深不同与土壤水蒸发在理论上具有一定的数值关系。由于机理模型本身的复杂性,潜水埋深在耕层附近的研究并不完善,再者由于土壤空间异质性导致机理模型在国内推广与使用具有局限性[25,27,31]。目前,国内从事土壤水盐运移研究的工作人员主要研究大气降水后,由地表向下淋溶的过程,或者是将淋溶与蒸发结合起来,单独的从浅埋深潜水与溶质浓度对蒸发影响机理的研究较少。基于此,溶质浓度对潜水蒸发及植物生理指标的研究有助于进一步完善土壤水盐运移的机理研究,强化土壤水盐动态在地下水作用下的影响是解释并防治土壤盐渍化的有效手段。
2 土壤水盐运移模型的研究
土壤非饱和水是陆地植物赖以生存的水源。随着研究的深入,经济发达的国家对土壤水盐运移领域进行了大量的研究,处于干旱、半干旱地区的国家对土壤水的研究尤为重视[6]。已有研究表明,影响潜水蒸发的因素主要有气象因素、潜水埋深、土壤质地、植被因素和地下水矿化度等[32-33]。此外,土壤冻结和温度梯度等因素也可能引起土壤盐渍化[34-36]。以上影响因素中,气象因素与海陆分布及所处的温度带关系密切;土壤质地与成土母质、成土过程关系密切;植被因素受自然因素与人为因素的双重影响,在生态学方面的研究较多;潜水埋深及地下水矿化度受自然因素与人为因素的双重影响,随着社会经济的发展,潜水埋深及地下水矿化度受人为影响越来越大,打井、灌溉等人为活动可改变潜水埋深及地下水矿化度。潜水埋深与地下水矿化度在影响土壤水盐运移数值模型研究中极为重要[37-39]。研究表明,不同地下水埋深和地下水矿化度均与潜水蒸发有数值关系[7],并且以此引出了关于土壤水盐运移的经验模型、半经验—半机理模型和机理模型[40]。
2.1 常用的潜水蒸发经验公式
土壤水分含量随着地下水位的变化而变化。一般情况下,当地下水埋深较浅时,受土壤温度与势能梯度的影响,地下水与土壤水作用强烈。地下水分通过土壤毛管被输送至地表,在土壤水分蒸发至大气的过程中,土壤盐分在地表积累。在地下水作用下水分运动过程中,以阿维里扬诺夫经验公式为主的潜水蒸发经验模型被广泛应用。潜水蒸发受潜水蒸发强度的影响,影响潜水蒸发强度的因素主要有潜水埋深、地下水矿化度、土壤质地和植被等因素。其中裸地潜水蒸发以潜水埋深的影响最为深刻。科研工作者通过对观测数据的分析及回归,得出了一系列实用性较强的线性或非线性公式。
2.1.1 阿维里扬诺夫经验公式。在多种潜水蒸发经验公式中,阿维里扬诺夫公式是较常用的公式之一[41],具体表示如下:
(1)
式中:E表示潜水蒸发;E0表示水面蒸发强度(理想蒸发强度);H表示潜水埋深;Hmax表示地下水极限埋深(潜水蒸发为0时的埋深,约为1.5~4 m);n为参数,一般为1~3。
该公式可以直观地反映出潜水蒸发与潜水埋深的关系,一定范围内,随着潜水埋深的增加,潜水蒸发在不断减小,潜水埋深越浅,蒸发越大;当潜水埋深为0时,潜水蒸发接近水面蒸发。该公式由于其简单易懂,在我国潜水蒸发研究中应用广泛,相关科研工作者在利用该公式时也对其进行改进,以适应当地的蒸发类型[42-43]。但是,阿维里扬诺夫经验公式需要确定水面蒸发、地下水极限埋深以及n的大小,地下水极限埋深一般较难准确确定,n为其中要求的参数,受气候条件、土壤类型影响较大,在年际变化影响下,其值不稳定,一定程度上为模型的精度造成影响。
2.1.2 沈立昌双曲线公式。由于阿维里扬诺夫经验公式在实际应用的过程中,有时不能很好地满足我国的实际,1978年,沈立昌提出了沈立昌双曲线模型[44],模型的具体表示是:
(2)
或
(3)
式中:E表示潜水蒸发,单位mm·d-1;H表示某段时间由潜水蒸发引起的平均地下水位消退值,单位mm·d-1;E0为某时段内平均日水面蒸发,单位mm·d-1;h为某时段内平均地下水埋深,单位为m;u为变幅带给水度;K表示土质、植被及水文地质条件等其他综合因素的影响经验常数;a,b为指数。从以上公式可以看出,沈立昌双曲线模型符合潜水蒸发特性。

2.1.3 叶水庭指数型公式。由于阿维里扬诺夫经验公式与沈立昌双曲线公式均有用到Hmax,叶水庭等(1977年)为了避免使用Hmax,根据实测数据提出了潜水蒸发指数型模型[45],具体表达式为:
E=u×h=E0×e-aH
(4)
式中:h为计算时段内潜水位变幅;u为潜水变幅带土壤给水度;a为衰减系数;E0为水面蒸发;H为潜水埋深;该公式又被称为叶氏公式,在潜水埋深较浅时拟合度较好。
2.1.4 幂函数公式。对大量的实测数据进行拟合时,发现幂函数公式也有一定的实用性,通过回归拟合分析,得出幂函数的公式表达式为:
C=E/E0=a×H-b
(5)
式中:E为潜水蒸发;E0为水面蒸发强度;H为潜水埋深;a,b为经验常数;该公式与叶氏公式类似,在潜水埋深较浅时拟合效果较好。
2.2 半经验—半机理模型
半经验—半机理模型是在一定物理研究背景的基础上,通过大量观测数据拟合而成的经验公式。目前应用较广的半经验—半机理模型是清华雷志栋公式,简称清华公式。清华公式是根据非饱和土壤水稳定流理论,分析潜水蒸发与水面蒸发量,潜水位埋深的关系[46]。该公式在实践过程中常被应用[47-48]。付秋萍等[47]通过试验对几种经验模型及清华公式验证发现,清华公式在新疆地区具有广泛的通用性,拟合精度相对较高;而阿维里扬诺夫公式在潜水埋深较浅时拟合程度较好,潜水埋深较深时,试验值与观测值差距较大;叶氏公式与幂函数公式均在埋深较深时拟合程度较差;相比之下,清华公式的拟合精度最高,幂函数拟合程度最差。
清华公式是雷志栋根据近代土壤水动力学的研究成果,提出了潜水蒸发的半经验—半机理公式,具体表达式如下:
E=Emax(1-e-ηE0/Emax)
(6)
式中:η为经验常数,与土质及地下水位埋深有关;Emax为潜水埋深为H条件下的潜水极限蒸发强度,Emax=AH-m,其中A、m为随土壤而异的参数。清华公式既考虑了土壤疏水性,又考虑了表土蒸发,该式结构较为完整,拟合精度高,具有广泛的通用性。但是,由于清华公式中参数求解比较繁琐,限制了其在实际中的应用。在对η进行求解的过程中,唐海行、付秋萍等均给出了η的求解方法,并在实际求解中应用较广[49-50]。
2.3 机理模型的研究
地下水作用下的水盐运移常用的土柱试验是用时较少,受天气变化及季节性影响较小的试验方法。土柱试验能够较好地消除土壤空间异质性所造成的差异,常用来模拟一维状态下土壤水盐的淋溶与蒸发,它的发展为水盐运移的机理模型提供了理论基础。1856年,Darcy通过饱和砂层的渗透试验得出了通量q(单位时间内通过单位面积土壤的水量)和水力梯度成正比的达西定律[6]:
(7)
式中:L为渗流路径的直线长度;H为总水头或总水势,ΔH表示渗流路径始末断面的总水头差;Ks表示孔隙介质透水性能的综合比例系数,即单位梯度下的通量或渗透流速,单位与速度单位相同;该式是在均质土壤恒定流动状态下得出的[1]。之后在达西定律和连续方程的基础上,Richards在1931年以偏微分方程描述非饱和土壤水盐运移情况,建立了多孔介质中水流运动方程[51]。土壤盐分方程依据质量守恒方程和土壤溶质通量方程获得。根据对流弥散理论所描述的土壤溶质迁移方程和质量守恒方程,获得了描述土壤溶质运移的基本方程,通常称为对流弥散方程[52]。目前,对饱和与非饱和多孔介质中水流运动与溶质运移相关数值模型的描述主要以Richard方程和对流—弥散方程为基础[53-54],在此基础上对Richard方程与对流—弥散方程改进。不同领域学者研究开发出多种模拟饱和、非饱和多孔介质中水盐运移的数值模型。
水文方面常用的比较典型的数值模型包括由美国农业部盐土实验室开发的HYDRUS-1D、HYDRUS-2/3D软件[55-56],该软件主要包含饱和非饱和土壤在不同维度下水、溶质与热运移。随着各专业领域的需求与发展,HYDRUS软件可在多重溶质交互作用下的溶质运移、优先流、胶体运动及湿地模块的过程中应用[57]。MODFLOW是20世纪80年代由美国地质调查局的McDonald和Harbaugh于20世纪80年代开发出来,是一套用于多孔介质中地下水流动数值模拟的软件[58-59]。它的显著特点是运用了模块化的结构,一方面将许多具有类似功能的子程序组合成子程序包;另一方面用户可按实际工作需要选用其中某些子程序包对地下水运动进行数值模拟。此外,在MODFLOW的基础上,加拿大采用现代可视化技术开发研制了Waterloo Hydrogeologic Inc,该系统是目前国际最为流行、且被国际同行一致认可的三维地下水流和溶质运移模拟评价的标准可视化专业软件,在模拟地下水运动方面具有重要价值[60-61]。在农业方面应用较广的数值模型有美国Oregon大学Boersma等人开发的用于土壤-植物-大气连续体中一维水、溶质、热运移的CTSPAC软件[31];还有美国环保署开发的用于饱和非饱和土壤与地下水中二维水、溶质(ABJ)和热运移的2DFATMIC软件[62];比利时Leuven 州Katholiek大学水土管理研究所开发的土壤、植物和包气带环境(一维)中水、溶质和热运移的WAVE软件[63];澳大利亚CSIRO基于有限差分法开发的土壤-植物-大气系统(一维)中能量、水、碳和溶质运移的WAVES软件[64],这些软件的开发利用既方便了土壤水盐及热运移的研究,又为盐渍化土壤的开发利用与治理提供了重要的理论依据。
此外,随着计算机技术的应用与发展,传递函数模型、人工神经网络预测模型和时间序列模型等在实际土壤物理研究及土壤水动力学的研究过程中也被广泛应用[65-66]。传递函数模型简单,易于操作,不需要大量的观测试验,并且不需要考虑土壤的饱和导水率、孔隙度和溶质运移路径等物理特性,在田间尺度上,对土壤溶质迁移研究相对方便。人工神经网络预测模型同样开拓了土壤溶质运移研究的空间尺度,根据人脑的原理,反复运算,提高模型的拟合精度,该模型可通过增大样本量的方法缓解土壤空间变异性所造成的差异,目前被越来越广泛地利用。
我国地下水作用下水盐及热运移数值模拟研究相比国外起步较晚,约开始于20世纪70年代,经过数代科学家的努力,在土壤物理学及地下水动力学方面取得了重大成果[6,67-69],并且开发出了一些具有实用价值的软件。例如,中国地质大学开发的渗流计算程序和三维有限元地下水计算程序,西安地质学院开发的不规则网络有限差分程序等,但是,目前我国水盐运移方面的软件普遍存在可视化程度低,数据处理功能相对较弱的问题,所以推广有一定的困难[70]。
对物理模型而言,计算的可靠性在于对运移模型中溶质运移过程相应的精确性与参数的选取[71]。对物理模型的研究大多通过实验室对物理过程模拟研究,尤其以基础参数准确性最为关键,如导水率与扩散率等的确定对模型模拟精度起到至关重要的作用;其次,科研工作者对土壤微观机制及田间土壤理化过程的认知分析程度是模型选择应用的重要基础。随着学科交叉的深入,不同领域科研工作者的交流有助于模型在各个领域内的推广,同时也可推动土壤物理学的发展。目前应在土壤水盐运移模型基础上,通过土柱试验与田间观测确定盐渍土研究方面的参数,针对不同区域选用最优土壤水盐运移模型。
3 人工控制地下水作用下土壤水盐运移研究
自然界土壤的空间异质性与地下水位的差异,在一定程度上限制了对潜水埋深条件下土壤水盐运移状况机理的研究。土壤水盐动态与土壤水盐运移机理的研究,是认识土壤盐化与碱化的形成和改良的基础[72]。为了便于对土壤水盐运移动态的研究,科研工作者普遍采用人工控制潜水埋深及潜水矿化度的方式研究,并发现潜水埋深及矿化度是引起土壤水盐运移动态及影响土壤水盐运移的重要因素。研究人工控制潜水埋深与矿化度的方法,主要通过室内或田间土柱试验进行。在人工控制潜水埋深及矿化度的基础上,对土柱采用一系列的处理措施[73]。例如史文娟等对土柱土壤进行夹砂处理,模拟研究不同土层土壤水盐运移动态变化,并对土壤夹砂处理下的水盐动态做机理性解释[74]。刘广明等通过人工控制潜水埋深模拟研究了同一潜水埋深下,不同土壤质地对土壤水盐运移动态及影响,揭示砂粒、粉粒和黏粒对土壤水分蒸发和淋溶及土壤盐分动态的影响[75]。杨建峰等通过人工控制不同潜水水位,研究了松嫩平原土壤水盐运移动态变化及苏打盐渍土形成及变化的机理性问题[76]。这些研究进一步解释了我国影响土壤水盐动态的因素,也为我国土壤水盐运移模型的研究奠定了理论基础。国外也进行了大量土柱试验的研究,与我国不同的是,国外的土柱实验的研究大多都以模型为基础,一方面是对模型的验证,另一方面是对模型参数的校正。例如Lehmann等[77]做的沙柱试验说明在对称波动的地下水位作用下,土壤含水量差异较大,此时通过Richards方程所模拟的土壤含水量与潜水埋深的关系与试验观测数据差异较大,说明Richards方程需要考虑土壤水分特征曲线的滞后效应,考虑了滞后效应的Richards方程所做的模拟与试验观测的吻合度较高。同样,由于土柱试验相比于大田试验具有很强的可控性,Todd和Whalley等均利用传感器测定土柱中水盐动态,并且通过土壤中水盐传导在传感器上的反应,验证传感器的稳定性[78-79]。土柱试验的发展在一定程度上解决了大范围内土壤空间异质性的问题。例如,研究黑钙土与栗钙土的渗透性、水盐动态等问题只需用特定材料做土柱,然后取土,按一定的试验方法操作即可,极大地方便了科研工作的开展。但是土柱试验仅仅是实验室内的一部分,并不能代表大田的实际情况,所以和大田的实验结果仍有较大差异。将土柱试验与大田观测相结合,理清室内土柱试验与大田试验的物理过程,通过校正土柱模拟所得到的方程,完善相关模型,增强模型的精度与普适性。
4 结论与展望
随着人工控制潜水作用下土壤水盐运移研究的发展,国内外土壤物理研究均取得了长足的进展,土壤水盐运移经验模型和数值模拟应用的范围、精度均得到了加强。多学科交叉为土壤物理及水动力学的发展提供了方法,例如遥感影像、同位素[80-83]检测等均为土壤水动力学与盐渍土的理论研究与治理提供了新方法。水盐运移模型的研究越发成熟,尤其是随着信息技术的发展,潜水埋深对不同物理性状土壤机理性模型及经验模型的参数研究得到了补充,对世界盐渍土的治理提供了重要的理论支持。
尽管土壤物理学已经得到了长足的发展,土壤盐渍化的治理也得到了重大发展,但是土壤盐渍化问题依然存在,并且还有扩大的迹象。在未来,随着人类对农作物产量与质量的需求不断提升,土壤水盐运移及模型的发展方向逐渐明确。
(1)土壤水盐运移模型应该全面考虑,在水盐运移研究基础上对土壤水、肥、气和热方面进行模拟,以增加土壤保水保肥保墒的性能,为盐渍土的改良奠定基础。
(2)应该将田间尺度与室内土柱试验模拟试验相结合,同时将田间尺度与区域尺度土壤水盐运移相结合。在田间尺度上,将地统计学与土壤水盐运移模型相结合,是解决田间尺度水盐运移模拟的有效途径;区域尺度上,将室内水盐运移模型与遥感原理相结合,通过遥感影像技术,动态统计区域潜水分布及潜水特性。遥感原理与水盐运移模型应用相结合,使土壤水盐运移模型具有更精确的预测功能,也为盐渍土的改良提供强大的理论支持。
(3)对机理模型而言,参数的优化和完善一直是国内外学者研究的重点和热点。参数的可靠性是机理模型应用与发展的基础。在今后的工作中,根据土壤空间异质性与地区间的差异完善土壤参数的测定,建立全球性的潜水对土壤水盐运移的影响网络是未来土壤水研究的重要内容。
(4)对于埋深在1 m以内不同矿化度的潜水对土壤水盐运移机理性的研究,国内仍然比较匮乏。埋深较浅的潜水与大气作用极为密切,该深度埋深潜水作用下导致土壤水含量较高,通过洗盐对土壤的改良相对容易。对该部分机理的研究,不仅可以完善浅层地下水作用下土壤水盐运移动态的空缺,而且有助于提出新的改良土壤的方法。

