居民区电动汽车充电负荷建模研究

， ， ， ，

(1.郑州大学 电气工程学院 河南 郑州 450001； 2.国网河南省电力公司 嵩县供电公司 河南 洛阳 471400)

0 引言

大量电动汽车充电负荷的接入加重了配电网高峰负荷时段的压力.建立电动汽车充电负荷模型,以制定引导用户采取有序充电的措施，对配电网的优化运行具有重要意义.

文献[1-3]研究了电动汽车充电负荷的影响因素，表明其充电负荷具有时空不确定性与复杂性.文献[4]提出了充电功率、行驶里程、开始充电时刻对居民区电动汽车充电负荷的影响.以上研究未给出具体的电动汽车充电负荷建模方法.文献[5]采用排队论模拟电动汽车的充电特性并导出了相应的充电负荷模型.文献[6]分析了影响电动汽车充电负荷建模的主要因素，提出了概率负荷建模方法.

本文首先根据锂电池简化模型与其恒流、恒压充电模式，给出了单台电动汽车充电功率.然后分析居民区电动汽车电池剩余荷电量(residual state-of-charge，SOC0)的随机特性，文献表明用正态分布可较好地表示电池SOC0的随机特性；之后分析了电动汽车返回居民区的时间特点，并参阅文献可知，泊松分布可表示其返回时间(电动汽车接入充电桩时间)的随机特性.最后通过蒙特卡洛法生成相应数组，建立了居民区电动汽车充电负荷模型.通过对仿真结果的分析，给出了电动汽车用户有序充电及供电部门采取分时电价措施的相关建议，以减轻负荷高峰段压力，并减少电动汽车用户的充电成本.

1 单台电动汽车充电功率计算方法

可用于电动汽车的充电电池种类很多，锂电池在比能量、比功率、体积等方面均优于其他类型电池，是未来电动汽车动力电池的发展方向.

锂电池多采用恒流恒压阶段充电法，充电过程中电池可视为1个受控电压源和1个恒值内阻串联而成的简化模型.

锂电池输出电压Ub可表示[7-9]为

Ub=E-(KQNi)/(0.1QN+h(t))-(KQNh(t))/(QN-h(t))+Ae-Bh(t)-R0i，

(1)

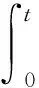
(2)

其中：Ub为锂电池输出电压；i为充电电流；QN为电池标称容量；SOC0为电池初始荷电量；UN为电池标称电压；E0=αUN；R0=βUN/QN；A=γUN；B=ν/QN；K=ρUN/QN.

E0、R0、A、B、K表达式中的系数α、β、γ、ν、ρ与锂电池型号有关，可查阅锂电池相关资料得到.

锂电池的整个充电过程中，恒压阶段所占时长很小，并且充电功率很小，对电动汽车充电负荷的影响可忽略，只需考虑恒流充电过程.

令恒流阶段的充电电流i=I0(I0<0)，将I0代入公式(1)得到Ub.

充电过程中电动汽车电池的充电功率为

Pb=-Ub·I0.

(3)

此外，电动汽车充电桩拓扑结构中的整流、低通滤波和DC-DC变换器等模块的效率高、损耗小，可忽略不计.

综合以上分析，可认为电动汽车的充电功率即为锂电池的充电功率.单台电动汽车的充电功率与电动汽车电池剩余荷电量相关，居民区电动汽车充电负荷又与电动汽车返回时间直接相关.因此，基于单台电动汽车充电功率模型，考虑电动汽车电池剩余电量及电动汽车返回时间的随机分布特性，是居民区电动汽车充电负荷建模的关键.

2 电池SOC0随机分布特性分析

居民区的电动汽车因车主工作性质、充电习惯等因素的影响，其充电电池SOC0具有一定的随机性.相关文献指出，当样本空间变大时，电池的SOC0呈现一定规律性.大数定律及中心极限定律表明：当样本空间足够大时，充电电池SOC0这一随机变量的概率分布近似服从正态分布.因此用正态分布表示电动汽车电池SOC0的分布特性.

参阅一定的文献可知，除出租车等职业需长期保持车辆近满电量外，在多数的居民区中，用户的电池剩余荷电量大约在0.2～0.45之间，相对较为稳定[10].在这种情况下，可取电池SOC0正态分布的均值μ为0.3，方差为0.02.其他类型居民区的电动汽车电池SOC0的均值与方差可通过分析其职业特点取相应合适的数值.

2.1 电动汽车返回行为的特点

居民区的电动汽车依据居民的职业、生活习惯，在某个时间段内将大量返回，呈现一定的稳定性；前一辆电动汽车返回居民区与否对其他车辆没有任何影响，即无后效性；电动汽车返回居民区这一事件时刻在发生，又具有一定的普遍性.大量文献表明居民区电动汽车的返回行为与泊松分布的特点相吻合，为此可用泊松分布表示其返回时间的随机性.

2.2 两段泊松分布的负荷特性研究

现实生活中，居民的返回行为比我们想象的更为复杂，用单段泊松分布表示这一行为特性，太过粗糙.为更加真实的反映其时空随机性，用两段泊松分布表示电动汽车返回行为更为精确.

假设小区有6 000个住户，平均每天有25%的用户需要充电(约1 500辆)，这些电动汽车每天在18:00—24:00全部返回(这里做了近似处理，少量电动汽车其他时间点返回，不会影响其整体充电负荷).单位时间片段取t=5 min，充电电池SOC0服从N(0.3,0.02)的正态分布，电动汽车返回时间分别服从单段与两段泊松分布.

两段泊松分布下，返回时间18:00—24:00分为两段，时间段18:00—20:00返回车辆数服从参数为λ1的泊松分布，时间段20:00—24:00返回车辆数服从参数为λ2的泊松分布.泊松分布参数λ1、λ2的计算方法为：每一时段到达车辆总数/该时段单位时间片段总数.第一时段返回车辆数占总车辆数的比值记为k，则两段泊松分布下的充电负荷生成步骤如下.

1) 令算法循环次数Y=1 000，每次记为yi，且初始值y1=1.

2) 用蒙特卡洛法生成两个时段到达充电站的电动汽车数量的数组分别为Nc1，Nc2.

Nc1=[n1,1,n1,2,…,n1,M]～P(λ1),M=T1/t，Nc2=[n2,M+1,n2,M+2,…,n2,M+L]～P(λ2),L=T2/t，其中：Nc1、Nc2为两个阶段到达车辆数的相应数组；M、L为两个数组中元素的个数；λ1、λ2为两阶段泊松分布的对应参数；n1,j、n2,k为两个单位时间片段内到达车辆数(1≤j≤M,M+1≤k≤M+L)；T1、T2为两段泊松分布第一时段、第二时段的总时长.

3) 用蒙特卡洛法生成电池SOC0的随机数组，S=[s1,s2,…,sZ]～N(0.3,0.02)，Z=T/t，其中：0.3、0.02为SOC0服从正态分布下的均值与方差；Z为数组S中元素的个数；T为总时长，即18:00—24:00.

4) 对数组Nc1、Nc2中的每个元素按下标j、k的大小顺序生成新的数组Nc=[n1,n2,…,nz].式中n为第z个单位时间片段到达站内的车辆数(1≤z≤Z).

5) 将步骤3)中的数组S代入公式(1)～(3),求出单辆电动汽车的充电功率Pi=[p1,p2,…,pZ].

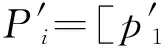
7) 令yi=yi+1.

单段泊松分布下电动汽车充电负荷的计算方法与两段泊松分布相同，在此不再赘述.

令第一时段返回车辆的比值k=75%(约1 100辆)，得到的充电负荷曲线如图1所示.图1的横坐标0～12代表前日18:00—次日6:00，图2、图3中横坐标含义与图1中的相同.因电池充电时间多为8～12 h，次日6：00时刻多数汽车已充电结束，充电负荷也变小，因此假设次日6:00所有电池充电结束，不会对负荷建模有太大影响.

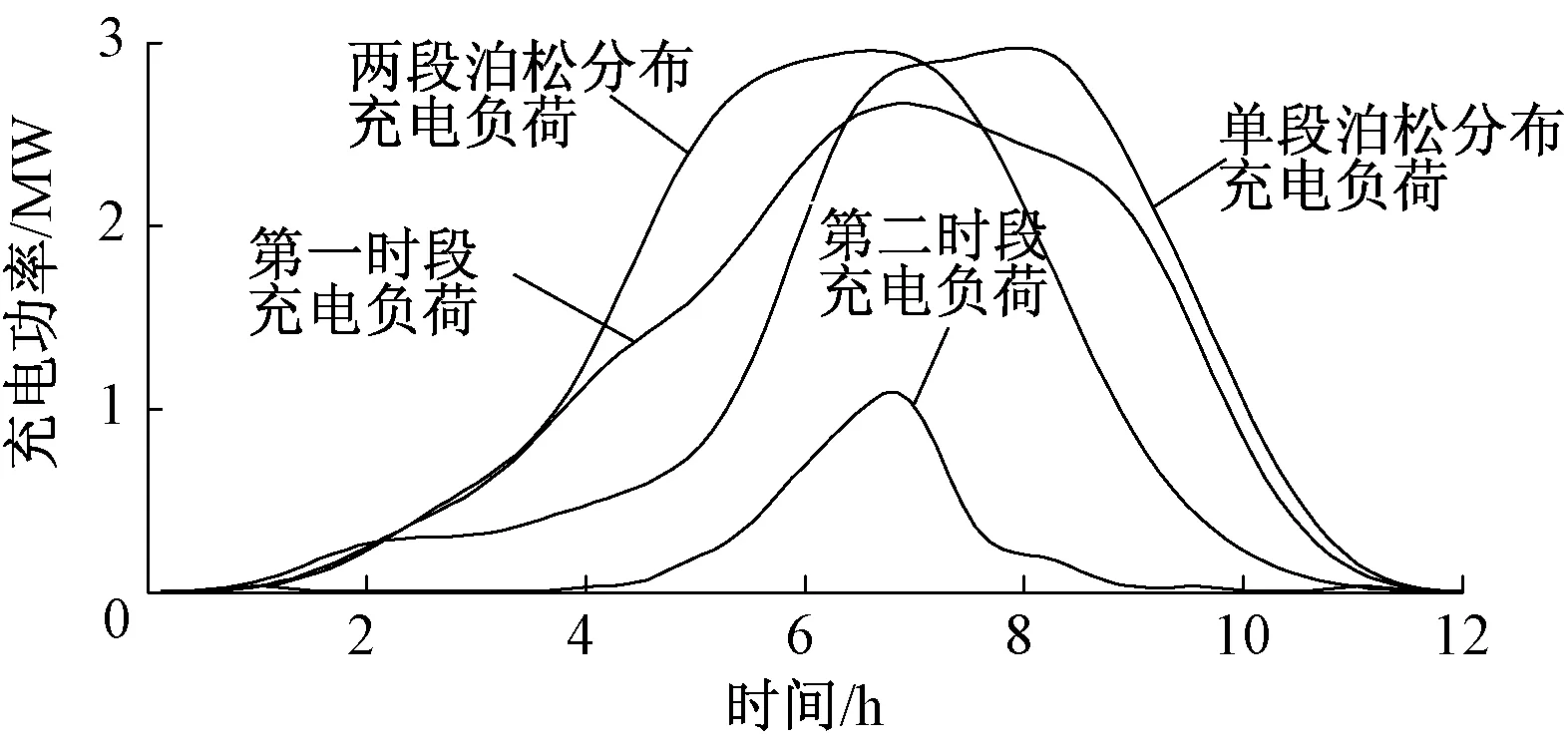
图1 两阶段泊松分布与单段泊松的充电负荷曲线图Fig.1 The charging power curve of two-stage Poisson distribution and single-stage Poisson distribution

由图1可知，两段泊松分布的峰值要比单段泊松分布的峰值出现的早，这与第一时段返回车辆数占较大比例刚好吻合.可见两段泊松分布表示车辆返回行为的随机性比单段泊松分布更精确，也更加符合居民真实的生活状况.

这样，用蒙特卡洛法生成电池SOC0的随机数组，并代入公式(1)～(3)，再生成一天内某些时段居民区充电站的进站车辆数，即可得到居民区电动汽车的充电负荷.

3 电动汽车充电负荷建模

3.1 电池SOC0的均值对充电负荷的影响研究

居民的职业类型不同，其用车行为会有很大的差异，因此他们对电池SOC0有不同的需求.比如公职人员，他们的电动汽车电池SOC0的均值取为0.3基本就可以满足日常要求，而出租车用户因其职业特点，其电动汽车需经常保持近满电状态.

因此研究电动汽车充电负荷受电池SOC0均值的影响，并从配电网优化运行角度找出电池最佳的SOC0，可为电动汽车用户的出行计划及电网部门采取分时电价激励措施提供一定的指导.令电动汽车电池SOC0的均值分别为0.1、0.2、0.3、0.4、0.5，其充电负荷如图2所示.

图2 SOC0服从不同均值的正态分布的充电曲线图Fig.2 Charging curve of SOC0following normal distribution with different means

由图2可知，电池SOC0的均值越大，即电池剩余荷电量越多，电动汽车充电负荷的峰值愈小，但这显然不利于用户的出行，也不符合多数居民日常生活习惯.如上文分析，除出租车等类似职业需经常保持其用车满电量，大部分居民区的居民可在其电动汽车电池SOC0不多的时候再去充电.因此电动汽车SOC0的均值处于0.25～0.35之间最符合大多数居民的充电习惯.

3.2 不同k值对充电负荷影响研究

居民因日常出行习惯的不同，其用车行为与充电时间也具有不确定性.这一因素致使第一时段返回车辆的数量不同，即电动汽车接入充电桩的时刻不同，得到的充电负荷也将有所差异.现令k值分别为10%、30%、50%、70%、90%来模拟电动汽车接入充电桩的时间差异.依据不同k值生成的充电负荷分析k值合理的范围，即汽车接入充电桩的合适时间，对引导电动汽车用户采取有序充电措施有一定的指导意义.k值分别取10%、30%、50%、70%、90%时，其对应的第一阶段返回电动汽车数量分别为150辆、450辆、750辆、1 050辆、1 350辆.

仿真得到的电动汽车充电负荷如图3所示.图3表明：第一时段接入充电桩的车辆较少时，充电负荷峰值不会太高，且峰值出现时刻较晚.第一阶段接入充电桩的车辆较多时，峰值出现时刻较早，会加重负荷高峰段的供电压力.从电动汽车有序充电角度考虑，k值控制在40%～60%之间为宜.

图3 不同k值的充电功率曲线图Fig.3 The charge power curve with different values of k

3.3 电动汽车有序充电措施

通过上文分析可知，第一时段到达的电动汽车数量愈多(k值越大)，即接入充电桩的车辆越多时，充电站的充电负荷峰值出现越早，会加重负荷峰段的压力，造成供电紧张，从用户与供电部门角度考虑，可采取如下有序充电措施：

1) 电动汽车用户可合理安排自己的日常出行计划，使电动汽车电池SOC0处于0.25～0.35范围内再去充电，可维持充电站良好秩序.

2) 从供电部门出发，若相关部门能推出分时电价政策[10-11]，用户通过自主响应充电站推行的分时电价激励，可有效降低充电站的运营成本与电动汽车用户的充电成本，有效实现充电负荷的削峰填谷，实现双赢.

4 结论

本文在简化锂电池模型的基础上，给出了单台电动汽车的充电功率.依据电动汽车电池SOC0与电动汽车返回时间的特点，本文参阅相关文献，表明正态分布与泊松分布能较好地表示电动汽车电池SOC0与电动汽车返回时间的随机分布特性.由蒙特卡洛法生成电池SOC0和不同时段电动汽车返回车辆数的随机数组，仿真生成居民区电动汽车充电负荷.通过研究正态分布下服从不同均值的电池SOC0和第一时段电动汽车返回车辆数，即接入充电桩的车辆数这两个因素对电动汽车充电负荷的影响，本文给出了居民区电动汽车用户采取相应有序充电的措施与供电部门推行分时电价政策的相关建议，对减少电动汽车用户的充电成本与配电网的优化运行起到一定的指导意义.