基于EMD的井下近钻头振动数据分析

张 霞，张 涛，李玉梅，黄 升

(1.北京信息科技大学 信息与通信工程学院，北京 100101； 2.北京信息科技大学 自动化学院，北京 100192)

0 引言

在钻进过程中，井下异常振动会造成钻头损坏，钻具疲劳，甚至会使井眼轨迹发生偏离，增大发生钻井事故的概率。钻井行业每年因井下异常振动造成的经济损失高达数亿美元[1]。为缩短建井周期，降低钻井成本，快速有效地识别出井下异常振动是亟需解决的问题。

20世纪50年代，国内外学者开始对井下异常振动模型进行研究。井下异常振动模型可分为横向异常振动模型和轴向异常振动模型。韩春杰等[2-3]使用有限元分析法建立水平井横向振动模型，得到了水平井钻柱横向自然振动的频率分布规律，通过仿真和计算，证明通过调整钻速可减少横向异常振动的发生；使用有限元分析法建立水平井轴向振动模型并对其进行模态分析，得到轴向振动的固有频率和其与钻柱长度的关系，对该模型进行谐响应分析，得到振动幅度与振动固有频率与钻压之间的关系，通过数据仿真及计算，证明通过调整钻压可减少轴向异常振动的发生。

20世纪70年代，国内外学者开始对井下数据采集工具进行研究。井下数据采集工具按照传感器位置不同可以分为井下采集和地面采集两大类。狄勤丰[4]对钻柱振动信息测量技术进行了总结，发现地面采集工具的优势为对传感器性能要求相对较低，数据采集方便，劣势为数据丢失现象严重；井下采集工具的优势为数据基本不丢失，劣势为对传感器性能要求高，数据采集困难大。滕学清[5]对来自超深井的井下振动数据进行时域均值分析、峰值分析和均方根分析，以及频域的快速傅里叶分析，得到粘滑振动在时域和频域的特征。

经验模态分解算法(empirical mode decomposition，EMD)是一种新型自适应信号时频处理方法，特别适用于非线性非平稳信号的分析处理。孔凡国[6]将EMD算法应用于轴承振动信号的异常识别中，通过对轴承振动信号作EMD分解，提取出异常振动信号特征，可准确有效地识别出异常轴承振动信号。

为快速准确地识别出井下异常振动，本文提出了一种基于经验模态分解算法的井下异常振动识别方法。通过对原始井下振动信号作EMD分解，得到井下振动信号的本征模函数(intrinsic mode function, IMF),对IMF进行希尔伯特变换，得到井下振动信号的瞬时频率，根据瞬时频率，可识别出不同的振动信号。

1 数据分析方法

1.1 EMD分解算法

EMD分解算法是一种适用于非线性非平稳信号的新型时频分析方法，与短时傅里叶变换相比，其优势为可以预防频率混叠；与小波变换相比，其优势为不需提前确定分解基函数。EMD分解算法的实质是：将原始信号分解为一系列具有唯一瞬时频率的单分量震荡信号，分解过程如式(1)所示：

(1)

式中：x(t)为原始振动信号；fi(t)为分解后的第i个单分量振荡信号；r(t)为分解后的剩余分量。fi(t)的极值数目和其自身过零点数目相等或仅相差1，且每个fi(t)的上包络和下包络的局部均值为0。

1.2 希尔伯特变换

希尔伯特变换算法是求单分量信号瞬时频率的一种方法。计算过程如下：先求出单分量振荡信号的希尔伯特变换，如式(2)所示：

(2)

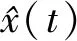
(3)

进一步可求得原始信号的瞬时频率ω(t)：

ω(t)=φ′(t)

(4)

原始振动信号的瞬时频率表示原始振动信号频率随时间的变化规律，从频率角度显示出振动信号的内在规律。

2 实例分析

井下振动包括正常振动和异常振动两种形式，其中异常振动又包括粘滑振动、涡动振动、跳钻振动3种形式。本文对柳贡惠[7]团队研发的井下近钻头数据采集工具采集的冀东某油田近钻头振动数据进行基于EMD分解的时频分析。

2.1 涡动振动数据分析

钻柱涡动[8]是指钻柱绕自身轴心自转的同时绕井筒中心公转，其中钻柱自转方向与公转方向相同的称为前向涡动，钻柱自转方向与公转方向不同的称为后向涡动，前向涡动如图1所示,后向涡动如图2所示，其中r为钻柱中心到加速度计的距离，R为井径，v为钻柱与井筒切点线速度，Ω为钻柱绕井筒轴心旋转角速度，ω为钻头转速。

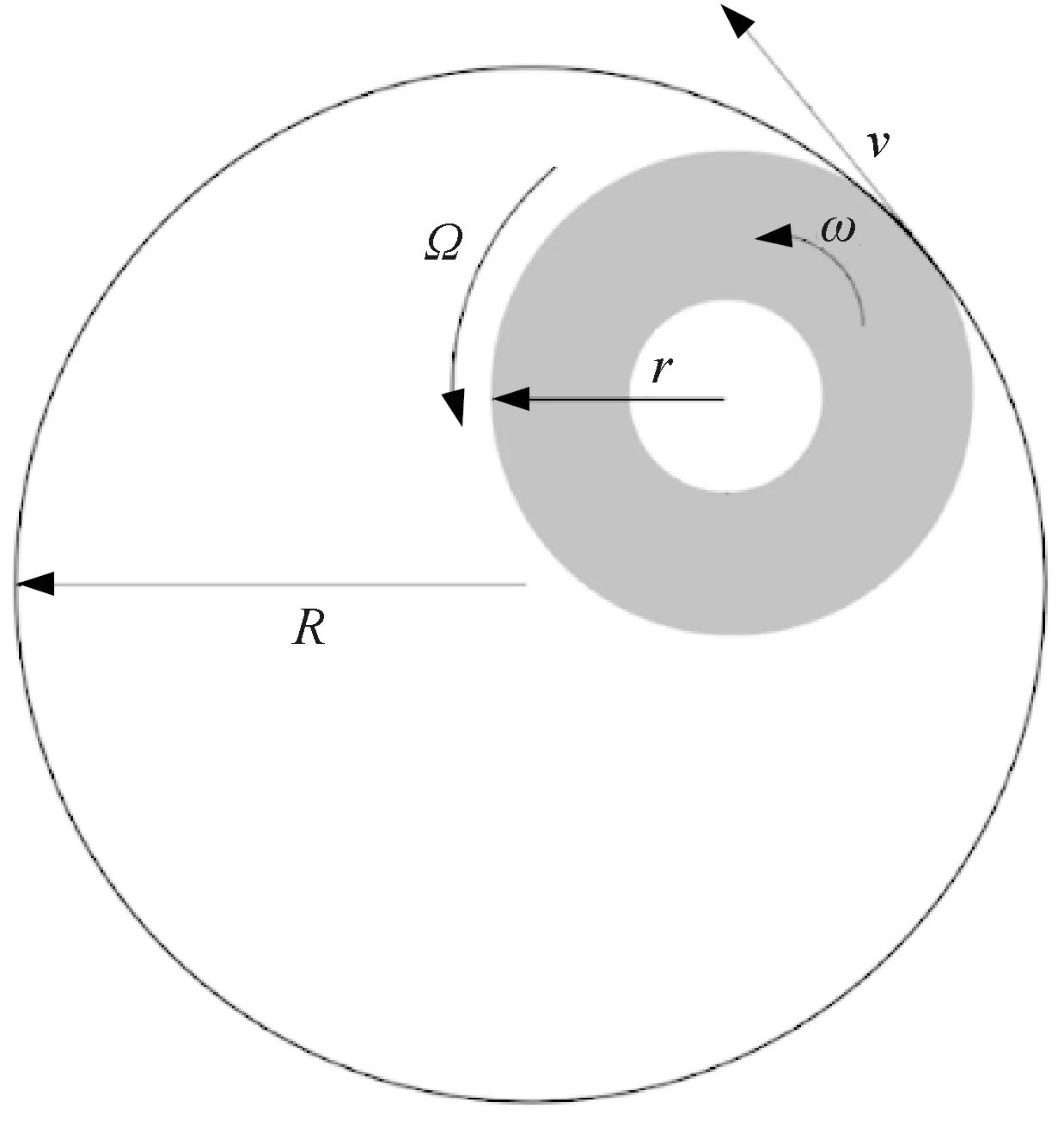
图1 前向涡动

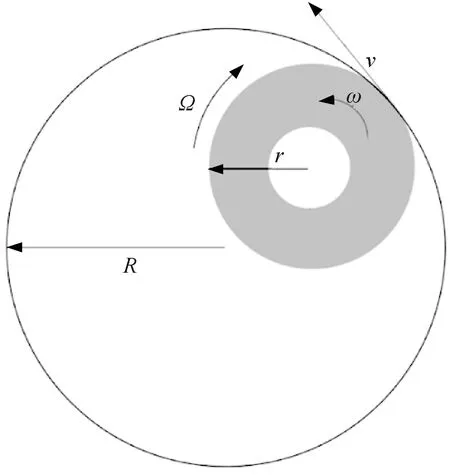
图2 后向涡动

分别对钻柱涡动横向振动信号、轴向振动信号作EMD分解，求得横向振动信号、轴向振动信号的瞬时频率，并画出其三维时频分析图，如图3、图4所示。

图3 钻柱涡动横向振动时频图

图4 钻柱涡动轴向振动时频图

由图3、图4可知，钻柱发生涡动时，在时域上，横向振动幅值最高可达35 m/s2,轴向振动幅值最高可达8.5 m/s2，即横向振动幅值远大于轴向振动幅值；在频域上，横向振动除0.3 Hz处的主频幅值大于5 m/s2外，还存在多个幅值大于5 m/s2的频率；轴向振动除0.3 Hz的主频幅值大于5 m/s2外，不存在其他幅值大于5 m/s2的频率。

2.2 粘滑振动数据分析

粘滑振动[9]是一种特殊的非线性运动，表现形式为：钻柱在钻进过程中发生非周期性的粘滞—滑脱现象。在粘滞阶段，钻柱内部发生轻微形变，处于蓄力阶段，表现为钻头转速降低直至停止；在滑脱阶段，钻柱形变瞬间释放，表现为钻头转速达到瞬时最大值，随后缓慢减小至停止，开始下一个粘滞阶段。

分别对钻柱粘滑横向振动信号、轴向振动信号作EMD分解，求得横向振动信号、轴向振动信号的瞬时频率，并画出三维时频分析图，如图5、图6所示。

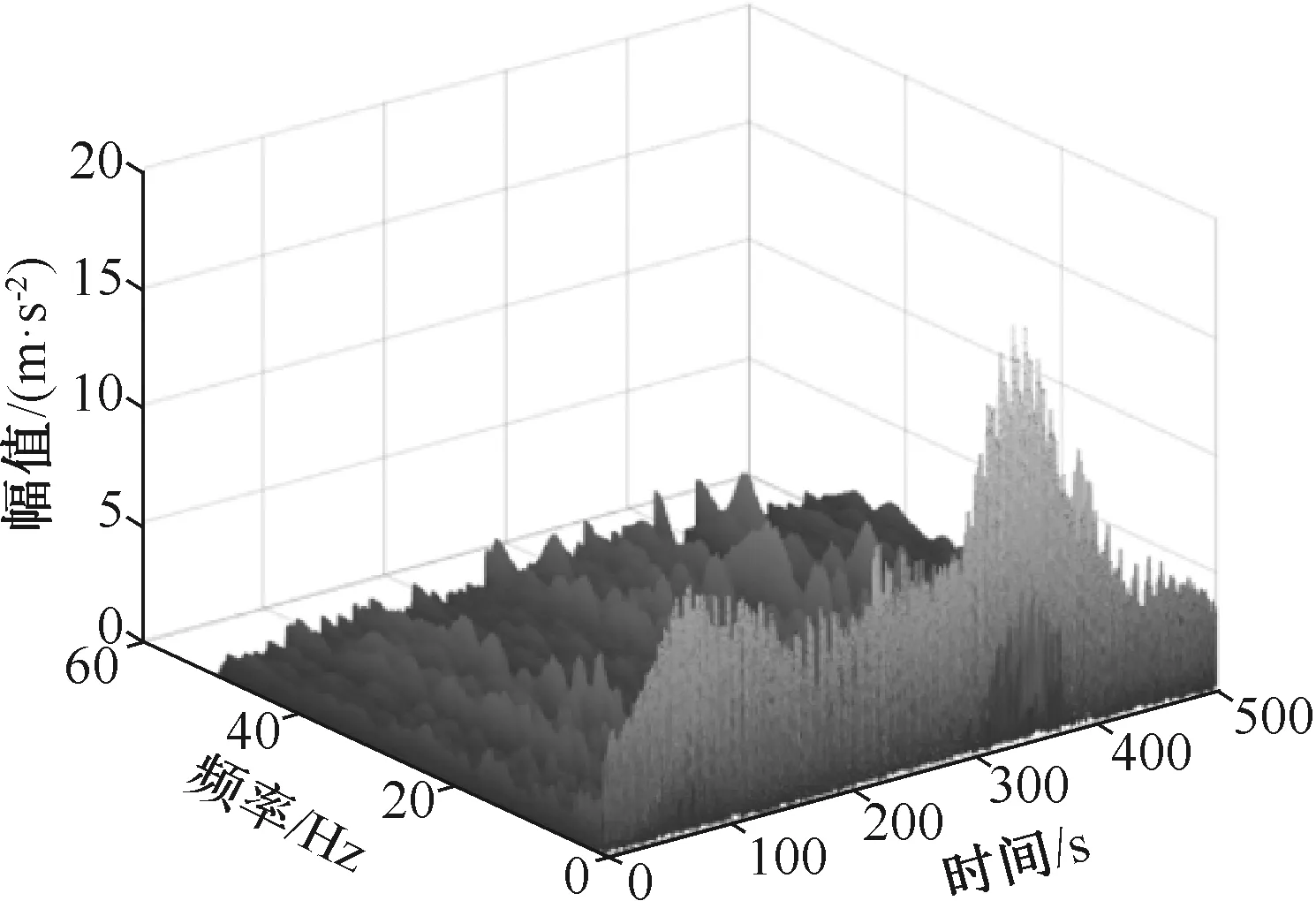
图5 钻柱粘滑横向振动时频分析图

图6 钻柱粘滑轴向振动时频分析图

由图5、图6可知，钻柱发生粘滑振动时，在时域上，横向振动幅值均大于5 m/s2，且幅值大小呈波浪形变化；轴向振动幅值均大于1 m/s2，且幅值大小呈波浪形变化。在频域上，横向振动在0.3 Hz处出现主频，主频幅值呈波浪形变化，除0.3 Hz的主频外，存在波浪形的高频信息。轴向振动的频域变换规律与横向振动的频域变化规律呈现同步性；横向振动、轴向振动的时域幅值波峰对应于频域频率高峰。

2.3 跳钻振动数据分析

跳钻振动[10]是一种以轴向振动为主的不规则振动，表现为在钻进过程中，钻头与岩层的瞬间脱离，产生跳动现象。

分别对跳钻振动的横向振动信号、轴向振动信号进行EMD分解，进而求得其瞬时频率，并画出时频分析图，如图7、图8所示。

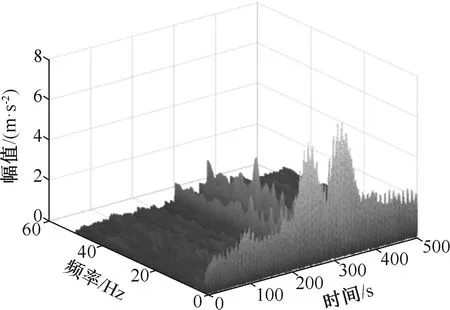
图7 跳钻振动横向振动时频分析图

图8 跳钻振动轴向振动时频分析图

由图7、图8可知，钻柱发生跳钻振动时，在时域上，轴向振动幅值大于横向振动幅值，其中横向振动幅值均大于2 m/s2，轴向振动幅值均大于5 m/s2；在频域上，横向振动与轴向振动频率变化呈一致性，横向振动频率幅值小于轴向振动频域幅值。

2.4 正常振动数据分析

在钻柱正常旋转钻进[11]过程中，发生横向振动、轴向振动幅值均较小的正常振动，对正常振动进行EMD分解，并求得其瞬时频率，画出时频分析图如图9、图10所示。

图9 钻柱正常钻进横向振动时频分析图

图10 钻柱正常钻进轴向振动时频分析图

由图9、图10可知，在正常钻进过程中，在时域上，正常振动的横向振动、轴向振动的幅值均稳定在3 m/s2左右，变化幅度不大；在频域上，横向振动和轴向振动均只有一个0.3 Hz的主频。

3 结束语

本文通过对井下近钻头处不同振动形式的振动信号做时频分析，得到不同振动形式在时频域的特征，结果表明，仅在时域或频域无法准确识别的振动形式，在时频域特征明显，易于区分。

1)发生涡动时，井下横向振动幅值远大于轴向振动幅值，同时横向振动除主频外存在其他明显频率，轴向振动仅存在一个主频。

2)发生粘滑时，井下横向振动、轴向振动幅值均呈同步的波浪形变化，且横向振动幅值大于轴向振动幅值，同时，每一个幅值峰值对应一系列的频率。

3)发生跳钻时，井下轴向振动幅值大于井下横向振动幅值，幅值呈波浪型变化，但横向振动与轴向振动幅值的变化不具有同步性；横向振动与轴向振动均存在一个主频，除主频外，横向振动的频率成分少于轴向振动频率成分。

4)正常钻进时，横向振动、轴向振动幅值稳定，且均小于5 m/s2，除主频外，不存在其他频率成分。

本文仅对数据进行了定性分析，没有得到定量的结论，仍有进一步研究空间。