新时期中职数学三角函数最值教学思路研究

郭建豪 周 捷

（潢川幼儿师范学校，潢川 465150）

引 言

新时期，国家对中等职业教育提供了更多的资源政策支持，但是由于中职生基础学习能力较薄弱，对数学知识不感兴趣，导致三角函数最值等重难知识点教学效果不佳。因此，本文结合新时期中职数学三角函数最值教学现状，对新时期中职三角函数最值教学思路进行了简单的分析。

我国教育事业进入了发展的关键阶段，中职教育发展也得到了教育界的大力关注。在这个大环境下，中职教育软硬件支持、教学质量、教学方法不断更新优化，取得了较大的成功。但是中职数学教学效果较差，特别是三角函数教学。因此，对新时期中职数学三角函数最值教学思路进行适当探究非常必要。

一、新时期中职数学三角函数最值教学现状

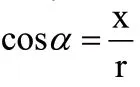
二、新时期中职数学三角函数最值教学思路

（一）阐述三角函数最值问题解析前提条件

三角函数性质、图像是求解三角函数最值问题的前提条件，只有中职生全面掌握三角函数对称性、单调性、定义域、奇偶性、值域及周期等基本概念，才可以根据图像正确描述三角函数性质，为三角函数最值问题解决奠定基础。如：已知原函数为y=cos4x，求其图像向左平移了π/2 单位后，又向上平移了2 个单位后得到的图像函数值域。

在上述问题解析过程中，首先教师可以根据原函数特点，为中职生详细阐述原函数定义域、对称性、周期及其在图像中分布情况。随后引导中职生根据定义推导出变化后图像函数。在这个基础上，进行函数最值求解方法讨论。

（二）合理应用三角函数数形结合解析法

考虑到中职生数学基础较差，单一定义解析推导的方式并不能保证其掌握三角函数最值解析方法，甚至会导致其对三角函数问题失去学习兴趣。这种情况下，教师就可以合理利用数学结合的方式。根据三角函数是从三角形边长中发展而来的这一特点，引入函数图像，将三角函数正弦、余切、正切、余弦等与三角形边长求解紧密结合。以降低三角函数最值问题求解难度，提高中职生对三角函数最值问题解析方法学习兴趣。

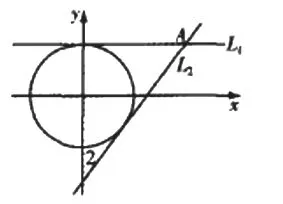
图1 函数图像

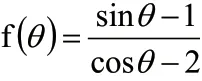
（三）拓展三角函数最值问题解析思路

在数形结合求解方法应用的基础上，为了培养中职生创新思维，教师可以利用均值不等式、三角函数有界性、配方法等方法，进一步拓展三角函数最值问题解析思路，保证三角函数最值问题教学效果。首先，利用均值不等式求解三角函数最值，主要是依据均值不等式使用条件一正、二定、三相等（参加均值不等式数字均为正数，数字的乘或和为定值，不等式等号成立的条件是在两数字相等时），进行三角函数最值求解。

其次，在基于三角函数有界性求解最值方法应用过程中，由于三角函数有界性求解主要是从三角函数值定义域入手，利用三角函数自身有界性，进行三角函数最大值、最小值求解。因此，基于三角函数有界性的三角函数最值求解过程中，可以首先利用三角函数有关公式，将其转化为asinx+bconsx=(x +ϕ)的形式，其中可以由点（a，b）的位置，结合tan确定。

如：求y= 的值域。

需要注意的是，在上述问题解析过程中，教师应以x 的定义域为教学重点。引导中职生回忆关于所求解函数的图像，以便其了解相关函数最大值或最小值位置。进而促使中职生可以举一反三的了解全部三角函数最值求解公式，并牢固掌握三角函数最值解析方法。

最后，在利用配方法求解三角函数时，教师可以结合具体例题，引导中职生将原函数配方为二元一次函数。根据二元一次函数定义，求解得出三角函数最值。如：求f（x）=cos2x+6sinx-2 的最值。

在上述问题解析过程中，教师可以首先带领中职生回顾以往学习的关于正弦函数与余弦函数转换方式，将f（x）=cos2x+6sinx-2 转换为f（x）=1-sin2x+6sinx-2=-（sinx-3）2+1

根据配方后公式，可以得出在sinx=1时，f（x）取得最大值，为-3，在sinx 为-1 时，f（x）取得最小值，为-15。

结 语

针对现阶段中职生数学基础差、缺乏教学情感等问题，数学教师应从求解三角函数最值问题的前提条件入手。从利用均值不等式求解、三角函数有界性求解、三角函数数形结合法求解等方面，为中职生解析求解三角函数最值的几种方法。以便降低中职生在三角函数知识学习方面的困难，保证教学过程顺利进行。