核心素养下中学数学基本不等式的新思考

李厚华

(重庆市荣昌中学校 402460)

基本不等式内涵丰富，从基本不等式的式子特征出发，不断地对解题过程进行分析、变形、转化、探究、思考、论证、创新，体会基本不等式解题过程的奥秘、简洁和严谨,同时去感受数学，打破固有思维，跳出自我的局限，增添我们学好数学的信心.理解并掌握以下基本不等式及其变形和推广.

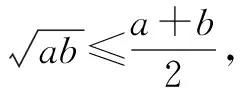
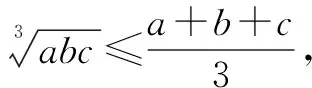
利用基本不等式，通过分析、推理、运算及其等价变形，得到“和”或“积”为定值，其解题的新思路、新方法有积、离、并、凑、引.

一、积——两两之积

式子与式子之积，分子与分母之积，变形运算后利用基本不等式求最值.

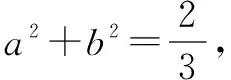
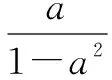
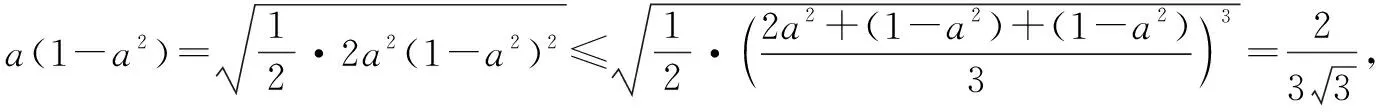
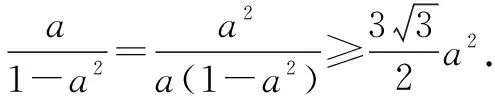
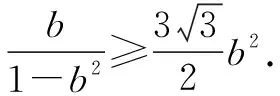
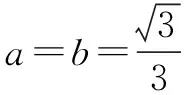
二、离——裂项分离

分子的次数不低于分母的次数的一个分式或几个分式之和,可进行整式裂项，分离成整式和真分式之和，再利用基本不等式求最值.

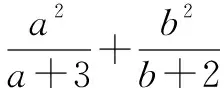
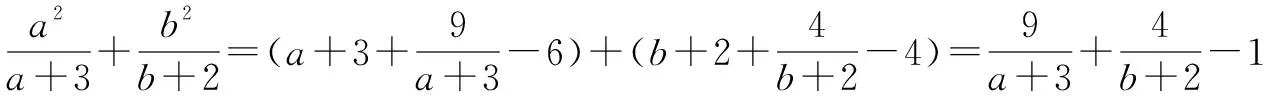
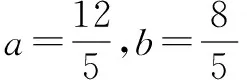
三、并——分组并项

条件之间、结论之间、条件与结论之间分组并项后，各组之间可利用基本不等式求最值，或各组之间变形运算后再一次利用基本不等式求最值.

分析本题条件中的第1项与结论的第2项合并，条件中的第2项与结论的第3项合并，……，条件中的第2018项与结论的第1项合并，合并后每一组利用基本不等式求最值.

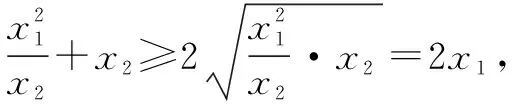
以上各式相加整理得

当且仅当x1=x2=…=x2018=1时取“=”，∴x1+x2+x3+…+x2018的最大值为2018.

四、凑——合理拼凑

采取合理拼凑式子，拼凑系数，得到新凑式子与待求式子之间的关系，通过转化、运算后利用基本不等式求出最值.

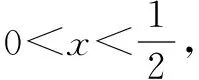
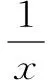
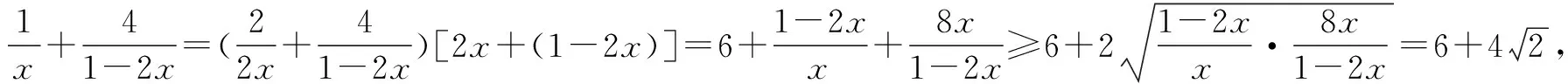
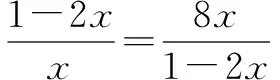
五、引——换元引入

引入新变量，用新变量将已知与结论、熟悉的等式、分散的条件联系起来，通过变形、转化后可利用基本不等式求最值.

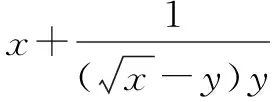
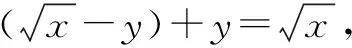
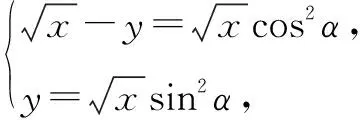
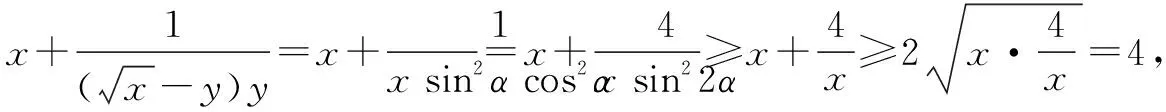
通过以上对富有挑战性的例题的探究，特别是学习了积、离、并、凑、引等解题的新思路、新途径，培养了我们严谨的数学学习习惯和良好的思维习惯,突出了数学抽象、逻辑推理、直观想象、数学运算、数据分析、数学建模等核心素养.总之，让我们多一些知识的新积累，多一些新视野，多一些新思考，多一些新智慧和力量，或者能够找到新发现、得出新规律、提出新结论，同时去感受数学的应用，走进数学,让创新能力、实践能力和数学核心素养在中学数学基本不等式的新思考中更充分地体现出来.