数学思想方法在三角形综合问题中的应用

李永革

(安徽省巢湖市第一中学 238000)

三角形问题形式多样，常见的有三角形计算问题、三角形形状判定、三角恒等式的证明，范围、最值问题，实际应用问题.解决三角形问题除了需要三角形性质，正、余弦定理，三角形面积公式等知识外，还与三角函数、三角恒等变换联系紧密.是三角、向量、函数、方程等知识的交汇点.教学中发现，对于一些综合程度较高的三角形问题，学生常感到思路不清，方向不明，运算受阻.为帮助学生较快地突破思维的瓶颈，理清推理和运算的思路，笔者在教学中注意运用数学思想方法探索解题思路，起到了较好的效果.现整理如下，以求教于同行.

一、方程思想的运用

三角形计算问题，等量关系的建立是关键.这里涉及两个问题，一是怎样获得等量关系(方程)，二是怎样确保方程可解.

1.怎样获得等量关系(方程)

等量关系的建立一般是借助正、余弦定理，三角形各种面积公式，有时要利用和(差)角公式、倍角公式以及向量知识.

另外，算两次的方法也是获得等量关系的重要途径.

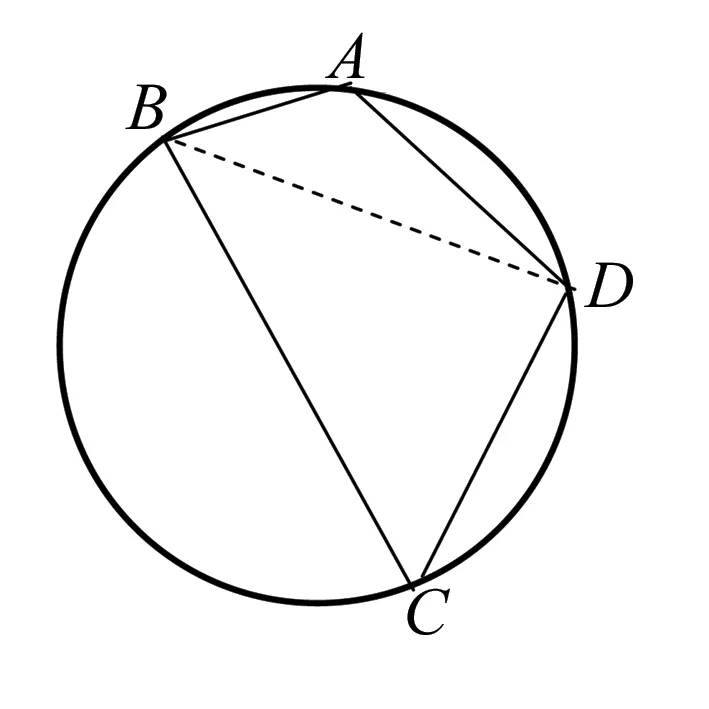
例1 已知圆内接四边形ABCD，AB=2,BC=6,CD=DA=4,求圆内接四边形ABCD的面积.

解连接BD，则四边形的面积

S=S△ABD+S△CBD

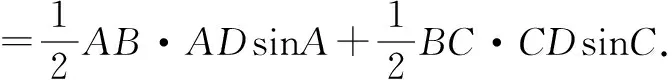
∵A+C=180°,∴sinA=sinC.

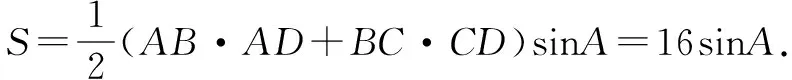
在△ABD中，BD2=22+42-2×2×4cosA=20-16cosA,

在△CBD中，BD2=62+42-2×6×4cosC=52-48cosC,

∴20-16cosA=52-48cosC.

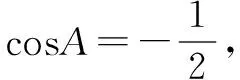
点评本题先后两次运用余弦定理计算BD，得出角的等量关系式.随后利用圆的内接四边形性质消去一个角.

2.怎样确保方程可解

有三个重要的技巧：一是如果遇到四种基本解三角形问题，要依据未知量唯一的原则从正、余弦定理，面积公式中选择恰当的等量关系.二是遇到多个未知量同时出现时，等量关系(方程)的个数不能少于未知量的个数.三是先用同一个字母表示图中某个三角形所有的边或角，再建立等量关系.

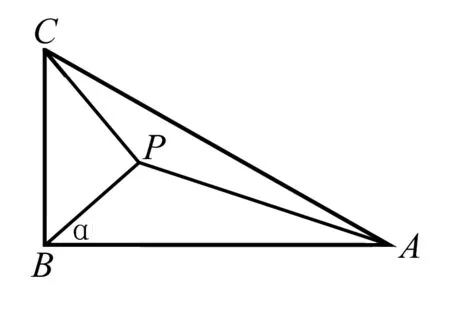
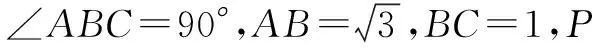
解(1)由已知得∠PBC=60°，所以∠PBA=30°.

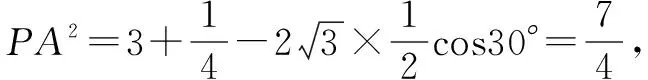
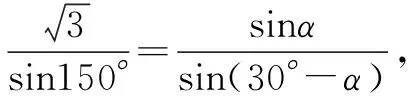
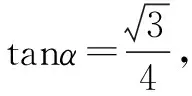
点评本题第(2)小题图中所有的三角形都不具备可解条件，于是先在直角△CBP中将PB用角α表示，再将△APB中的∠PAB也用角α表示.然后运用正弦定理建立方程.

二、函数思想的运用

三角形中取值范围问题和最值问题一般需要构建目标函数，将问题转化成求函数值域与最值问题.

例3 已知在△ABC中，内角A,B,C所对的边分别为a,b,c,且2acosC=2b-c.

近年来，我国农业农村电子商务快速发展，成效明显。贫困地区以及农产品成为农业农村电子商务发展最快的地区和领域。支撑农业农村电子商务发展的服务设施不断完善，产业链上下游联系更为紧密，服务内容不断拓展，新产业、新业态、新模式不断涌现。

(1)求角A的大小;

(2)若b+c=2,求a的取值范围.

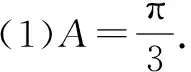
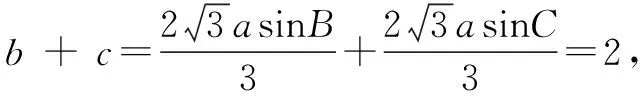
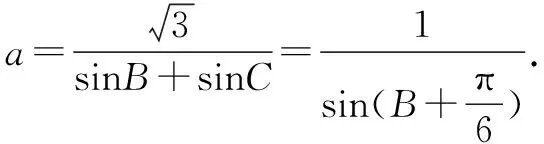
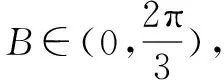
解法2(建立代数函数)：a2=b2+c2-2bccosA=b2+c2-bc=b2+(2-b)2-b(2-b)=3b2-6b+4,b∈(0,2),

∴a2∈[1,2),∴a∈[1,2).

三、消元的思想的运用

三角形计算问题常需要减少未知数个数，学生对角的消元不太熟练，常常缺少消角的意识和手段.灵活利用三角形内角和定理，已知角以及三角变换公式是消元的关键.

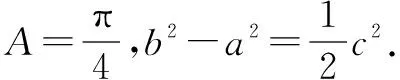
(1)求tanC的值；

(2)若△ABC的面积为3，求b的值.

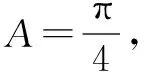
所以sin2C=2sinCcosC，解得tanC=2.

点评本题第(1)小题先将边的关系式转化成角的关系式，除了角A已知，角B和角C都是未知，考虑到题目要求的角是角C，所以需要消角B.运用了三角形内角和定理和诱导公式.

四、整体思想的运用

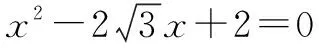
(1)求角C的度数；

(2)求AB的长度.

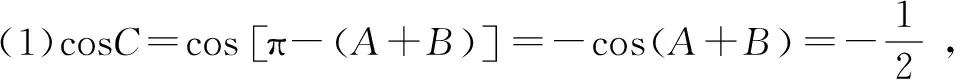
∴AB2=AC2+BC2-2AC·BCcosC=a2+b2-2abcos120°=a2+b2+ab

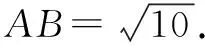
点评本题在计算中将a+b和ab当成整体，直接代值计算，减少了计算量.

五、化归思想的运用

化归思想在三角形问题中的应用最突出的表现是边角互化.比如利用正、余弦定理判断三角形形状.这类问题基本思路是：用正弦定理或余弦定理将所给条件统一为角之间的关系或边之间的关系.若统一为角之间关系式，则再利用三角恒等变换化简到角之间关系；若统一为边之间的关系式，则再利用代数方法进行恒等变形、化简，找到边之间的关系.一般地，若题设中含有角的余弦或边的二次式，则要考虑利用余弦定理进行转化；若题设中含有角的正弦或边的一次式，则要考虑利用正弦定理进行转化处理.

另外，在计算题中，为了减少未知量的个数常常需要边角统一.有时已知条件是边的关系，但结论却是求角，也需要边角转化.

六、模型思想的运用

人教A版必修五教材在学习了正、余弦定理之后分别介绍了四类基本的解三角形问题.并将各类问题的解题套路和解的情况做了详细的讨论，这就为学生处理各种具体的解三角形问题提供了数学模型.

人教A版必修五教材应用举例部分不仅把应用问题分为距离测量问题、高度测量问题和角度测量问题,而且配备的例题和习题中的每一组已知条件，常隐含着对这类测量问题在某种特定情境和条件限制下的一个测量方案，在这种情境与条件限制下，别的方案中的量可能无法测量出来，因而不能实施别的测量方案.所以每一道例题等于提供了一种测量问题的模型.遇到同类问题直接按这种方案测量即可.

数学思想是解题的灵魂，因此在教学中应注意思想方法的提炼，帮助学生把握问题本质，确定正确的思维方向，克服解题的盲目性.当然要顺利解答三角形综合问题，除了需要强化数学思想的指导作用外，还要具备较强的代数运算能力和三角恒等变换的能力.同时还要注意三角形自身性质等隐含条件的挖掘，防止错解和漏解.