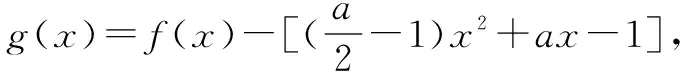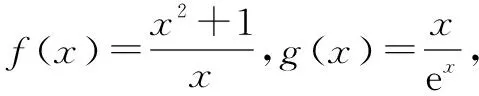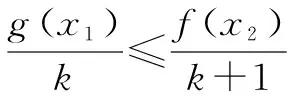新课标高考中导数内容常考题型拙见

胡彩云

(广西马山县马山中学 530600)

我们都知道在高中阶段，导数已成为研究函数性质的一种重要工具,尤其是利用导数探讨函数的单调性来解决相关的函数极值、最值、含参数以及不等式等问题，一直是高考命题的一大热点.现将常考的题型做一个小归纳.

一、导数的概念及其几何意义

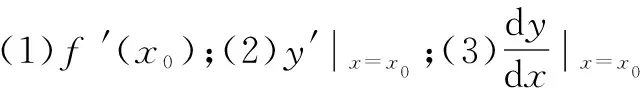
函数y=f(x)在点x0处的导数f′(x0)的几何意义是在曲线y=f(x)上点(x0,f(x0))处的切线的斜率．相应地，切线方程为y-y0=f′(x0)(x-x0)．

导数的几何意义是每年高考的必考内容，考查题型既有选择题、填空题，也常出现在解答题的第(1)问中，难度偏小，属中、低档题．常见的命题角度有：(1)求切线方程；(2)求切点坐标；(3)根据参数切线的性质求参数．

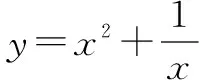
(2)已知直线l为曲线f(x)=x3+x-16的切线，且经过原点，则它们的切点坐标为____.

(3)若曲线y=f(x)=lnx+ax2(a为常数)不存在斜率为负数的切线，则实数a的取值范围是( ).

C．(0，+∞) D．[0，+∞)

二、求函数的单调性或用单调性解决简单的极值最值问题

这类问题要求考生会正确掌握求导公式和求导法则，理解并掌握用导数判断函数单调性的方法以及求极值、最值的方法步骤.函数的极值(最值)是每年高考的必考内容，题型既有选择题、填空题，也有解答题，难度适中，为中、高档题．常见的命题角度有：(1)知图判断函数极值(最值)；(2)已知函数求极值(最值)；(3)已知函数极值(最值)情况求参数值(范围)．而所有这些问题的解决，都依赖于用导数研究函数的单调性.其相关结论是：若f(x)函数在区间(a，b)上可导,则在区间(a，b)上f(x)递增⟺f′(x)≥0；f(x)递减⟺f′(x)≤0.

例2 (1)函数f(x)=x+lnx的单调递增区间为____.

(2)(2017课标2，理11)若x=-2是函数f(x)=(x2+ax-1)ex-1的极值点，则f(x)的极小值为( ).

A.-1 B.-2e-3C.5e-3D.1

(3)(2017课标3，理11)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点，则a=____.

三、利用导数解决不等式的证明问题

利用导数研究函数单调性来证明不等式 ，在高考的压轴题中是最常见的也是难度较大的问题.在证明的过程中，需综合考虑不等式相关的特点，然后通过恒等变形不等式或构造出函数，接着利用导数证明构造出的函数的单调性达到证明不等式的目的.常见的有：一是直接构造函数,然后用导数证明该函数的增减性；二是先把不等式变形后再构造函数,然后利用导数证明该函数的单调性,达到证明不等式的目的.三是转化为用导数求函数的最值来证明不等式.

例3 证明：当x>0时，x-ln(1+x)>0.

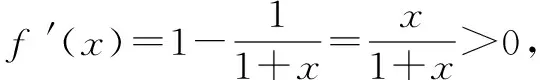
故有f(x)>f(0)=0即x-ln(1+x)>0.

例4 证明：当x>0时，x>sinx.

分析先把不等式变形为x-sinx>0，就转化为例3类的问题，用同样的方法即可证明.

例5 证明：当x≠0时，ex-x>1.

证明设f(x)=ex-x-1(x≠0)，则f′(x)=ex-1.

令f′(x)=0得到x=0，且当x<0时，f′(x)<0;当x>0时，f′(x)>0;

所以f(x)在(-∞,0)上单调递减，在(0,+∞)上单调递增.x=0为极小值点，也是最小值点.即f(x)>f(0)=0，ex-x>1.

当然，在利用导数证明不等式问题中，还有一类难度较大的题型，那就是构造函数，证明数列不等式问题，在这里就不做阐述和举例.

四、不等式恒成立问题的处理方式

所谓不等式恒成立，其实就是指函数无论取最大值或最小值时不等式都能成立.通过证明不等式的恒成立问题，将其转化成解决函数最值的问题，就可以利用其证明不等式是否成立.而要证明不等式的恒成立就会涉及参数的证明问题，通过变量分离，证明某个值大于或小于函数值，就可以证明不等式恒成立.也就是往往把变量分离后可以转化为m>f(x) (或m

而解决这类问题的策略常有：

①首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围.

②分离变量,构造函数,直接把问题转化为函数的最值问题.

当然，在高中阶段，导数相关的题型还有很多，比如存在性问题，实际应用问题等等，高考考查的题目灵活多变，常考常新.虽然在2018年理科高考压轴题中，考查不等式问题的难度稍有下降，但是还是会常考不衰.这类题目的解答过程中，教师应引导学生选择正确的切入点，构建出不等式，只有这样，才能准确地利用导数知识证明不等式是否成立.因此，在实际的教学中，教师必须组织、引导学生学好导数的知识，不仅为高考考一个好分数，更要为日后的学习微积分知识奠定坚实的基础.