构造“基本不等式”适用背景的六种变换
2019-02-15 08:27蔡勇全
数理化解题研究 2019年1期
蔡勇全
(四川省资阳市外国语实验学校 641300)
基本不等式是高中数学的重要内容,也是历年高考考查的热点,它的技巧性较强,体现在有些问题不能直接应用该结论求解,需要事先进行适当的恒等变换,构造出基本不等式的适用背景——“一正、二定、三相等”,即不仅表达式中含变量的项是正的,而且表达式中含变量的项的和取得最小值时,能凑出这些项的积为定值,或含变量的项的积取得最大值时,能凑出这些项的和为定值,还须此时含变量的项恰好相等,从这个角度来看,基本不等式也是教学中的难点之一.
一、常量逆代
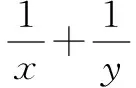
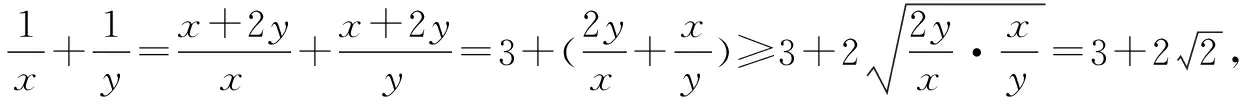
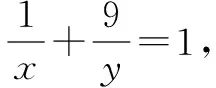
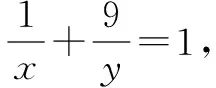
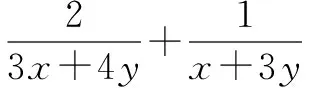
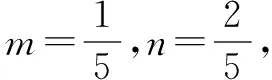
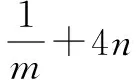
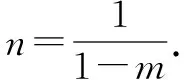
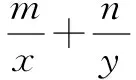
二、加几减几
例2 已知正数a,b满足ab-a-b-1=0,求a+b的最小值.
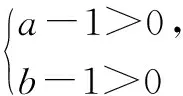
变式1 已知正数x,y满足3x+2y=xy,求2x+3y的最小值.
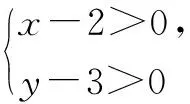
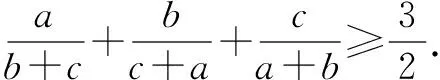

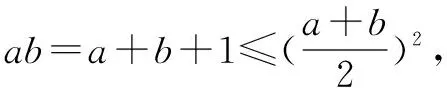
三、升次拆幂(项)
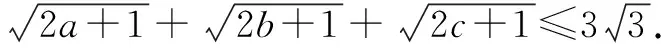
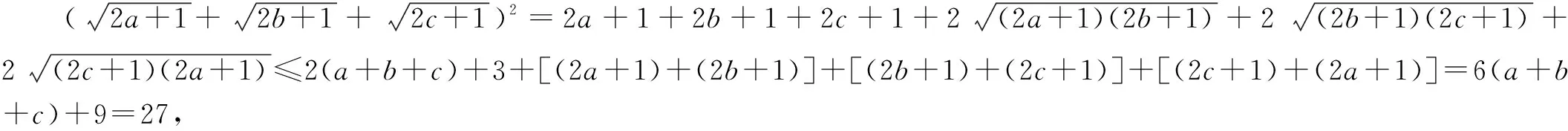
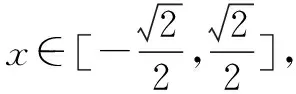
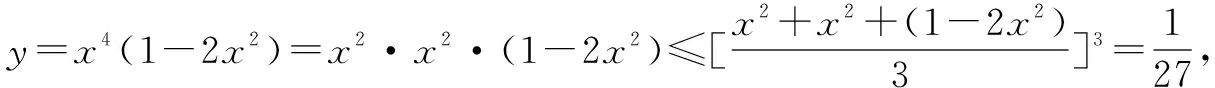
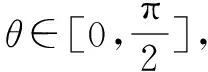
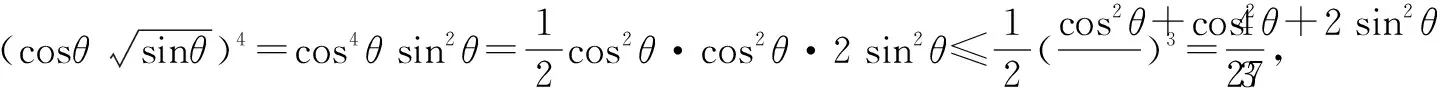
变式3 已知正数x,y满足x2y=2,求x2+xy的最小值.

评注例3及其两个变式采取了不同的升次拆幂技巧,其中,例3采取的是升次策略,将目标式升次到可以运用基本不等式的背景下,变式1是将目标式直接拆幂到可以运用基本不等式的背景下,变式2则是先升次再拆幂到可以运用基本不等式的背景下,而变式3是将目标式拆项到可以运用基本不等式的背景下,需要注意的是,不论是只升次还是先升次再拆幂,都要回归到原目标式本身.
四、换元引参
例4 已知a,b,c为△ABC三边的长,求证:abc≥(a+b-c)(b+c-a)(c+a-b).
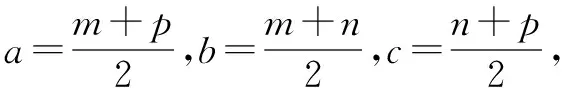

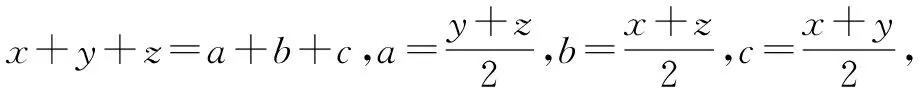
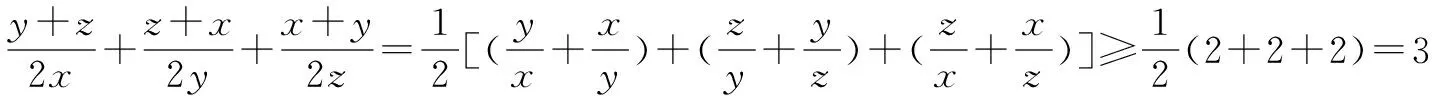
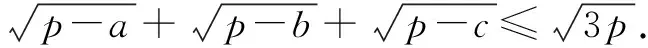
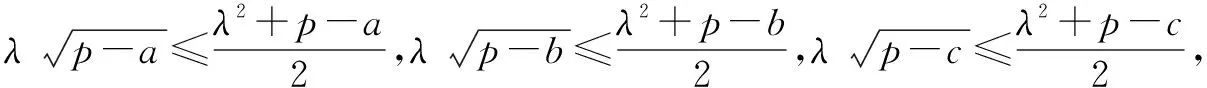
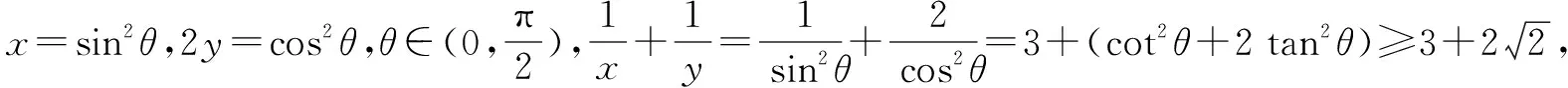
五、取倒反推
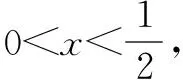
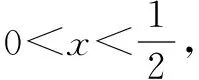
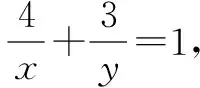
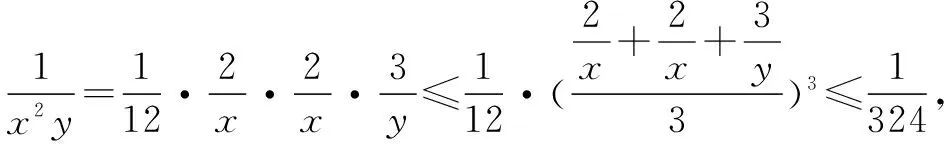

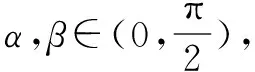
评注当条件与目标式之间的关系不明显或较为模糊时,运用取倒反推不失为一种迂进的间接策略,有利于使问题明朗化,取倒反推实际上也是正难则反思想的应用,如果从问题的正面求解比较困难,从问题的反面入手往往会事半功倍.
六、配添分离
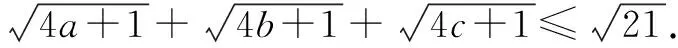
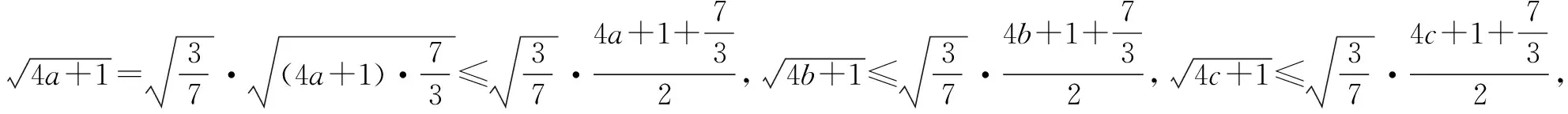
猜你喜欢
科技信息·学术版(2021年31期)2021-12-03
科学与财富(2020年3期)2020-04-02
中学生数理化·七年级数学人教版(2019年9期)2019-11-25
俪人·教师版(2016年20期)2017-03-02
中学生数理化·七年级数学人教版(2016年8期)2016-12-07
北京航空航天大学学报(2016年6期)2016-11-16
读写算·高年级(2009年8期)2009-08-12

