一道三角形面积最值的多角度赏析
2019-02-15 08:25沈培玲
数理化解题研究 2019年1期
沈培玲
(江苏省前黄高级中学 213161)
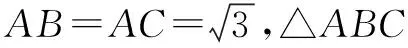
该试题是2017~2018学年第一学期江苏常州高三期末考试第14题,位于填空题最后一题,区分意味明显,可以看成是考查三角问题,也可以看成是考查圆的问题,是研究一题多解,一题一课的好题.本文将从以下几个不同角度进行分析.
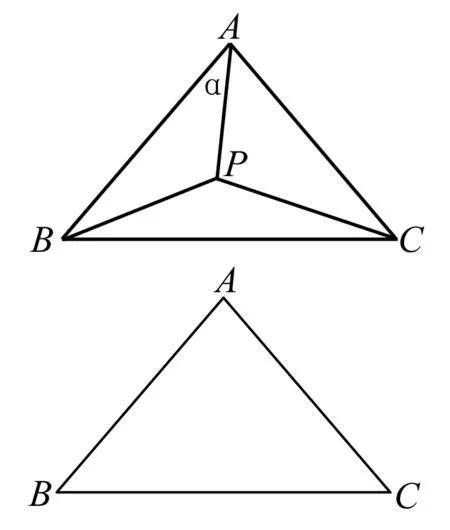
视角1 由等腰三角形联想到建系坐标处理.
解法一坐标化+轨迹思想处理(两圆有交点).
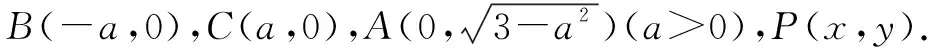
由3PA2=3⟹PA=1,说明点P在以A为圆心,半径为1的圆上,记为圆O1;
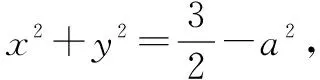
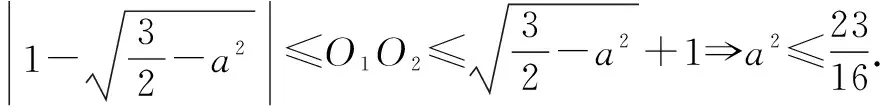

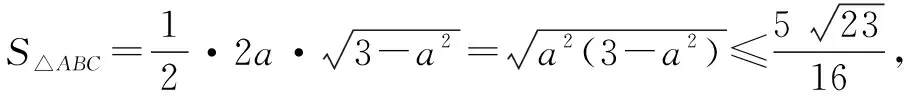
解法二坐标化+三角函数处理(方程有解).
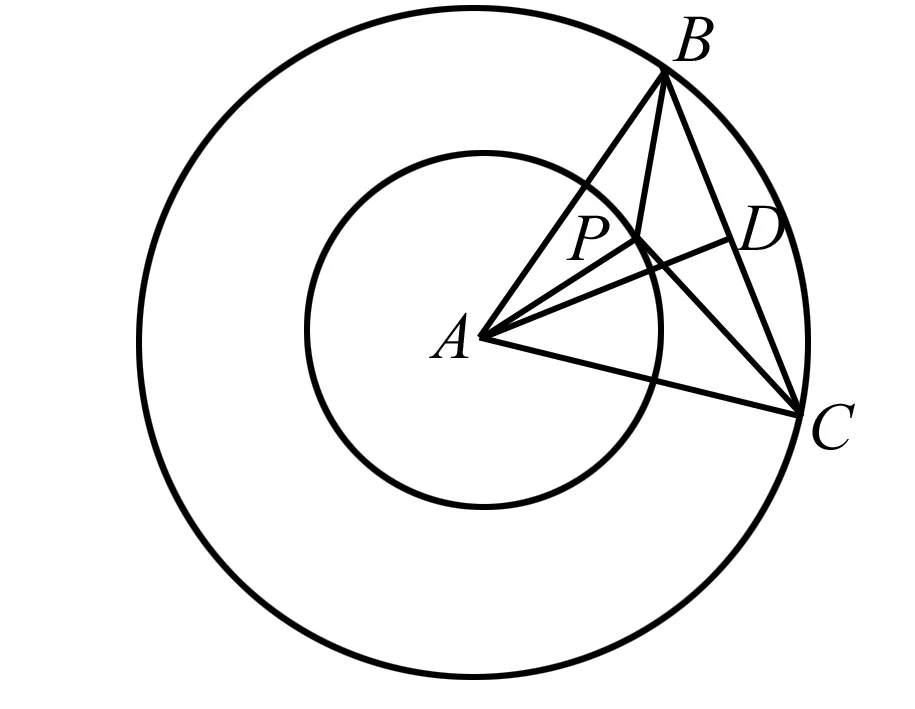
视角2 以点A分析,找点P的轨迹及B,C的轨迹.
解法三轨迹法+几何法处理.
因为PA=1,所以点P在以A为圆心,1为半径的圆上.
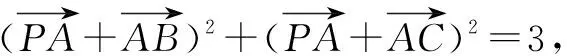
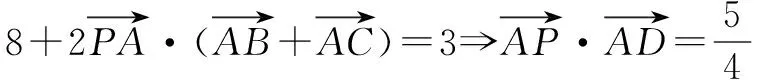
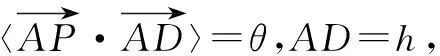
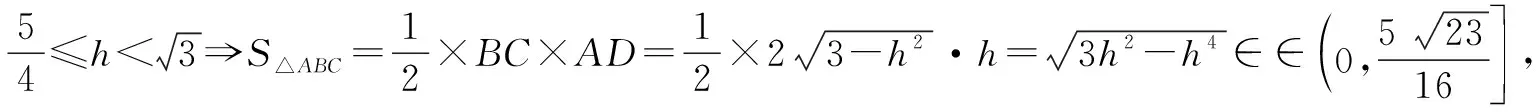
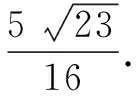
视角3 两次余弦定理,借助三角恒等变换即可求出∠BAC正弦的最大值.
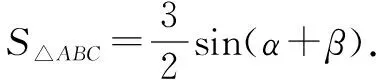
因为PB2=PA2+AB2-2PA·ABcosα;PC2=PA2+AC2-2PA·ACcosβ,
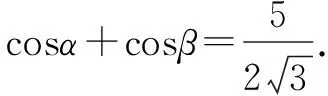
(部分学生就是猜的这个位置做对的,理由对称轮换是当PB=PC时取最值)
视角4 本题可以转化为求向量AB与向量AC的数量积的最小值.
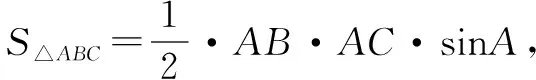
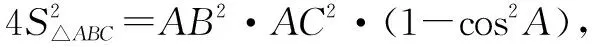
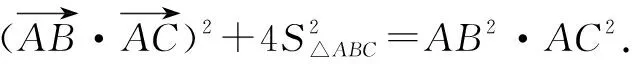
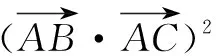
试题的讲评应充分考虑学生的数学能力的差异,一题多解给学生提供了较大的发挥空间.挖掘问题的本质,关注解题反思是一种高效的学习之路.
猜你喜欢
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
小学生学习指导(低年级)(2020年10期)2020-11-09
中学生数理化·七年级数学人教版(2019年10期)2019-11-25
中等数学(2018年1期)2018-08-01
数学教学通讯·初中版(2014年1期)2014-02-14
数学大世界·初中生辅导版(2010年2期)2010-03-08
数学教学(2009年12期)2009-01-20

