关于探索解题捷径的一种思考方法——全特征表述解题法的说明

李 伟

(辽宁省鞍山市第三中学 114012)

数学教学最大特点是重视解题思想方法的传授与积累，所以师生都热衷于积累解题方法和用方法引领解题.但如果我们对解题方法积累所造成弊端没有清醒的认识，那么，有时候后果将不堪设想，请看下面题例.

例题设函数f(x)=mx2-mx-1，对于任意x∈[1,3]，f(x)<-m+5恒成立，求实数m的取值范围.

解题分析解法一由已知得，只需mx2-mx-6+m<0对于任意x∈[1,3] 恒成立即可.这是我们再熟悉不过的问题了.思路马上出来：当m=0时，显然成立.当m≠0时，分m正、负，再讨论对称轴与[1,3]的三种位置关系(具体数学式子略去).这可谓是最一般、最常见的方法，也是解决这类问题的通用方法.显然，用这种方法解题要讨论七次，运算量也很大，所以，此种解法不仅叙述求解过程十分繁琐，如果是考试时遇到这种情况，将更加糟糕.

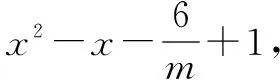
解法二的思路是注意到本题中二次三项式具备一次项、二次项系数均为m这一特征，所以通过不等式两边除m可化为一次项、二次项系数均为常数(在此只需讨论m正、负即可，运算量也很小)，这样对称轴就是定值，自然就不用讨论.

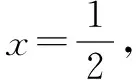
对比而言，易知解法二、解法三的简捷性选择、确定解题方法前，先思考题中已知和结论是否具有什么特征(特殊性)，并抓住其特征进行转化(化简)，再求解，而不是直接套用哪种解题方法去解题.正是这种思考，才能带来简捷的解法.

从事数学教学工作同仁都知道，简捷的解题思路和方法不仅提高解题效率，更是解题者追求的目标.从上例就看出借助“全特征表述解题法”这种思想方法寻找解题途径，以及其捷径性存在的原因.

什么是“全特征表述解题法”？“全特征表述解题法”是笔者创造出的词汇，将其界定为：在解题思路选择前，尽可能多地全面挖掘发现题目中已知和结论的特征，再根据所挖掘出的特征进行转化(化简)，然后再选用、确定解题方法.而不被题目表象所迷惑，简单直接套用某种定势的方法.换句话说，就是在解决具体问题中，应注意尽量回避直接选择一般的、具有通用共性的解题方法直接去求解；而是在全面挖掘其题目中已知条件和结论的特征后，再结合其特征进行转化后，再选择公式和解题方法去求解.为便于理解，请看下面举例：

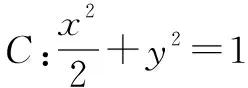
(1)当l与x轴垂直时，求直线l的方程;

(2)设O为坐标原点，证明：∠OMA=∠OMB.

解题分析问题(1)比较简单，解题分析略.

问题(2)、此问题是证明角相等.回顾高中数学教学中证角相等的方法有：向量中的求角公式、平面几何中的三角形全等、三角函数中通过三角函数值相等证角相等、解析几何中的两条直线夹角公式、斜率公式等.

回到本题全面挖掘题中条件和结论的特征：结论中角∠OMA、∠OMB的特征是两条直线与x轴相交、且对称交叉产生的.而直线的斜率既能描述直线的倾斜程度，又能揭示直线与x轴的夹角关系.所以说直线的斜率是包含本题所证明的结论中特征最多的量.因此，从两条直线的斜率k1、k2来思考问题的解决应该是比较简捷的方法.即通过斜率互为相反数(即k1+k2=0)来证明这两个角相等(∠OMA=∠OMB)应该是众多解法中比较简捷的，事实也是如此(具体运算和比较留给读者，这里就不进行具体运算比较了).

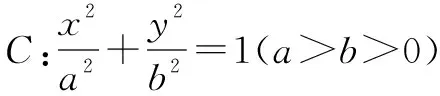
解题分析求离心率从解题方法来看，一是由已知条件分别求出a、c旳值；另一个是求出a、c的关系式.本题由题意知，应该是采取求出a、c关系式的方法求解.

由题中的条件知，借助线段的长度建立a、c关系式是显然的.回顾高中数学教学中求线段长的方法，有以下方法：

椭圆的定义等概念、两点间距离公式、正余弦定理、锐角三角函数、平面点的坐标与长度的关系等.回到本题全面挖掘题中条件和结论的特征：根据已知条件及画出的几何图形知，其条件的特征是“题中给出了等腰三角形一角(与x轴相关的角)和其边长；所以，设P点坐标后， 刚好由∠PF2F1=120°的外角、线段PF2及相关的坐标构成直角三角形的边，也就是说此直角三角形刚好反映出了P点坐标、半焦距、夹角之间的关系.经过对题中条件和结论的全特征挖掘后，可以说利用构造直角三角形解锐角三角函数的方法求解是比较简捷的.事实也确实如此(具体解题过程略).

举例3 (2018年理科全国二卷19题)设抛物线C：y2=4x的焦点为F，过F且斜率为k(k>0)的直线l与交于A、B两点，|AB|=8.

(1)求l的方程;

(2)求过A、B且与C的准线相切的圆的方程.

解题分析问题(1)比较简单，解法分析略.

问题(2)首先全面挖掘题中条件和结论的特征：题中大量涉及平面几何中圆，所以圆的性质一定是其鲜明特征.A、B是圆上的点，所以圆心一定在线段AB的垂直平分线上；圆的半径、弦心距与AB弦的一半可构成直角三角形.到此，这些特征对求解此题已足够用了.

设想，如果我们采取解析几何中常见的做法：即设圆心M坐标、设A、B点坐标(老师平时总是强调，解析几何要敢于设坐标)；然后根据圆上A、B两点到圆心距离等于圆半径和圆心到准线距离等于半径，列方程组；由此再求出圆心和半径，进而得到圆的方程.显然，解题过程很繁琐、运算量也比较大，此法能解该问题，但不可取.

对比两者解法分析：后者解法的思考是解析几何中最常规的想法，解法太具一般化了，不具备该题的特征，而具有一般性.前者解法是在充分挖掘题中条件、结论特征的所能提供的知识背景后，再将解析几何方法与平面几何方法进行适度整合，提出解题方案.所以解法具有本题的鲜明特征，其解法自然简捷.

类似的例子还很多，可以说包括高中数学各部分内容，由于其基本思想是一致的，所以在此不多赘述.至此，本文介绍了如何寻求解题简捷途径的一种思考，提出对题目进行全特征挖掘后，再确定解题方法这一解题策略.同时，也强调了在解题时，不要硬套某种解题方法等解题注意事项.供大家参考.